Index-p Abelianization Data of p-Class Tower Groups

Daniel C. Mayer^*

Naglergasse 53, 8010 Graz, Austria.

DOI: 10.4236/apm.2015.55029                

Abstract

Given a fixed prime number p, the multiplet of abelian type invariants of the p-class groups of all unramified cyclic degree p extensions of a number field K is called its IPAD (index-p abeliani- zation data). These invariants have proved to be a valuable information for determining the Galois group of the second Hilbert p-class field and the p-capitulation type of K. For p=3 and a number field K with elementary p-class group of rank two, all possible IPADs are given in the complete form of several infinite sequences. Iterated IPADs of second order are used to identify the group of the maximal unramified pro-p extension of K.

Keywords

p-Class Groups, p-Principalization Types, p-Class Field Towers, Quadratic Fields, Second p-Class Groups, p-Class Tower Groups, Coclass Graphs

1. Introduction

After a thorough discussion of the terminology used in this article, such as the logarithmic and power form of abelian type invariants in Section 2, and multilayered transfer target types (TTTs), ordered and accumulated index-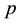 abelianization data (IPADs) up to the third order in Section 3, we state the main results on IPADs of exceptional form in Section 3.1, and on IPADs in parametrized infinite sequences in Section 3.2. These main theorems give all possible IPADs of number fields 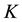with 3-class group 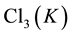of type.

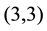Before we turn to applications in extreme computing, that is, squeezing the computational algebra systems PARI/GP [1] and MAGMA [2] -[4] to their limits in Section 5, where we show how to detect malformed IPADs in Section 5.1, and how to complete partial 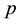-capitulation types in Section 5.2, we have to establish a com- ponentwise correspondence between transfer kernel types (TKTs) and IPADs in Section 4 by exploiting details of proofs which were given in [5] .

Iterated IPADs of second order are used in Section 6 for the indirect calculation of TKTs in Section 6.1, and for determining the exact length 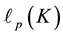of the 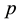-class tower of a number field K in Section 6.2. These

sophisticated techniques prove 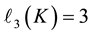for quadratic number fields 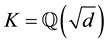with

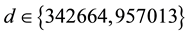(the first real quadratic fields) and 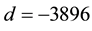(the first tough complex quadratic field after the easy 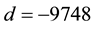( [6] , Cor.4.1.1), which resisted all attempts up to now.

Finally, we emphasize that IPADs of infinite -class towers reveal an unknown wealth of possible fine structure in Section 7 on complex quadratic fields having a 3-class group of type.

2. Abelian Type Invariants

Let be a prime number and be a finite abelian -group. According to the main theorem on finitely generated abelian groups, there exists a non-negative integer, the rank of, and a sequence of positive integers such that and

(1)

The powers, , are known as the elementary divisors of, since for each. It is convenient to collect equal elementary divisors in formal powers with positive exponents such that, , and

The cumbersome subscripts can be avoided by defining for each. Then

(2)

and we can define:

Definition 2.1. The abelian type invariants (ATI) of are given by the sequence

(3)

of strictly increasing positive integers with multiplicities written as formal exponents indicating iteration.

Remark 2.1. The integers are the -logarithms of the elementary divisors.

1) For abelian type invariants of high complexity, the logarithmic form in Definition 2.1 requires considerably less space (e.g. in Section 7, Table 2) than the usual power form

(4)

2) For brevity, we can even omit the commas separating the entries of the logarithmic form of abelian type invariants, provided all the remain smaller than 10.

3) A further advantage of the brief logarithmic notation is the independence of the prime, in particular when -groups with distinct are being compared.

4) Finally, since our preference is to select generators of finite -groups with decreasing orders, we agree to write abelian type invariants from the right to the left, in both forms.

Example 2.1. For instance, if, then the abelian type invariants in logarithmic form corre- spond to the power form and corresponds to.

Now let be an arbitrary finite -group or infinite topological pro- group with derived subgroup and finite abelianization.

Definition 2.2. The abelian type invariants of the commutator quotient group are called the abelian quotient invariants (AQI) of, that is,.

3. Index-p Abelianization Data

Let be a fixed prime number and be a number field with -class group of order, where denotes a non-negative integer.

According to the Artin reciprocity law of class field theory [7] , is isomorphic to the commutator

quotient group of the Galois group of the maximal unramified pro-

extension of. is called the -class tower group (briefly -tower group) of. The fixed field of the commutator subgroup in is the maximal abelian unramified -extension of, that is the (first) Hilbert -class field of with Galois group

. The derived subgroup is a closed (and

open) subgroup of finite index in the topological pro- group.

Definition 3.1. For each integer, the system

(5)

of intermediate fields with relative degree is called the -th layer of abelian un-ramified -extensions of. In particular, for, forms the bottom layer, and for, forms the top layer.

Now let be a fixed integer and suppose that belongs to the -th layer. Then the

Galois group is of finite index in the -tower group of

and the quotient is abelian, since contains the commutator subgroup

of.

Definition 3.2. For each integer, the system

(6)

of intermediate groups with index is called the -th layer of normal subgroups of with abelian quotients. In particular, for, forms the top layer, and for n = v, forms the bottom layer.

A further application of Artin’s reciprocity law [7] shows that

(7)

for every subgroup and its corresponding extension field, where is fixed (but arbitrary).

Since the abelianization forms the target of the Artin transfer homomorphism from G to H [8] , we introduced a preliminary instance of the following terminology in ( [9] , Dfn. 1.1, p. 403).

Definition 3.3. For each integer, the multiplet, where each member is interpreted rather as its abelian type invariants, is called the -th layer of the transfer target type (TTT) of the pro- group,

(8)

Similarly, the multiplet, where each member is interpreted rather as its

abelian type invariants, is called the -th layer of the transfer target type (TTT) of the number field,

(9)

Remark 3.1.

1) If it is necessary to specify the underlying prime number, then the symbol, resp., can be used for the TTT.

2) Suppose that. If an ordering is defined for the elements of, resp., then the same ordering is applied to the members of the layer, resp., and the TTT layer is called ordered. Otherwise, the TTT layer is called unordered or accumulated, since equal components are collected in powers with formal exponents denoting iteration.

3) In view of the considerations in Equation (7), it is clear that we have the equality

(10)

in the sense of componentwise isomorphisms.

Since it is increasingly difficult to compute the structure of the -class groups of extension fields in higher layers with, it is frequently sufficient to make use of information in the first layer only, that is the layer of subgroups with index. Therefore, Boston, Bush and Hajir [10] invented the following first order approximation of the TTT, a concept which had been used in earlier work already [11] - [15] , without explicit terminology.

Definition 3.4. The restriction

(11)

of the TTT, resp., to the zeroth and first layer is called the index- abelianization data (IPAD) of, resp..

So, the complete TTT is an extension of the IPAD. However, there also exists another extension of the IPAD which is not covered by the TTT. It has also been used already in previous investigations by Boston, Bush and Nover [12] [14] [15] and is constructed from the usual IPAD of, firstly, by observing that

can be viewed as and, secondly, by extending each

to the IPAD of.

Definition 3.5. The family

(12)

is called the iterated IPAD of second order of, resp..

The concept of iterated IPADs as given in Dfn. 3.5 is restricted to the second order and first layers, and thus is open for further generalization (higher orders and higher layers). Since it could be useful for 2-power extensions, whose absolute degrees increase moderately and remain manageable by MAGMA [4] or PARI/GP [1] , we briefly indicate how the iterated IPAD of third order could be defined:

(13)

3.1. Sporadic IPADs

In the next two central theorems, we present complete specifications of all possible IPADs of pro- groups for in the simplest case of an abelianization of type. We start with pro-3 groups whose metabelianizations are vertices on sporadic parts of coclass graphs outside of coclass trees ( [9] , Section 2, p. 410), ( [16] Section 10).

Since the abelian type invariants of the members of TTT layers will depend on the parity of the nilpotency class or coclass, a more economic notation, avoiding the tedious distinction of the cases odd or even, is provided by the following definition ( [5] , Section 3).

Definition 3.6. For an integer, the nearly homocyclic abelian 3-group of order is de- fined by its type invariants, where the quotient and the remainder are determined uniquely by the Euclidean division. Two degenerate cases are included by putting the cyclic group of order 3 and the trivial group of order 1.

In the following theorems, we use the identifiers in the SmallGroups Library [17] [18] .

Theorem 3.1. (First Main Theorem on, , and of small class)

Let be a pro-3 group having a transfer target type with top layer com- ponent. Let denote the defect of commutativity ([9] , 3.1.1, p.412, and 3.3.2, p. 429) of the metabelianization of. Then the ordered first layer and the bottom layer are given in the following way (exceptional cases in boldface font).

1) If is of coclass and nilpotency class, then

(14)

where generally.

2) If is of coclass and nilpotency class, then

(15)

where can be warranted for only.

However, if with, then

(16)

3) If is of coclass and nilpotency class, then

(17)

However, if, then

(18)

where the irregular case can only occur for even class and coclass, positive defect of commutativity, and relational parameter in ([5] , Equation (3.6), p. 424) or ( [9] , Equation (3.3), p. 430).

Proof. Since this proof heavily relies on our earlier paper [5] , it should be pointed out that, for a -group, the index of nilpotency is used generally instead of the nilpotency class and the invariant frequently (but not always) replaces the coclass in that paper.

1) Using the association between the identifier of in the SmallGroups Library [17] [18] and the transfer kernel type (TKT) [19] , which is visualized in ([5] , Figure 3.1, p. 423) and ( [16] , Figure 3), this claim follows from ([5] , Thm. 4.1, p. 427, and Tbl. 4.1, p. 429).

2) For, resp. with, the statement is a consequence of ([5] , Thm. 4.2 and Tbl. 4.3, p. 434), resp. ([5] , Thm. 4.3 and Tbl. 4.5, p. 438), when the association between the identifier of in the SmallGroups database and the TKT is taken into consideration, as visualized in ([5] , Figure 4.1, p. 433) and ( [16] , Figure 4).

3) All the regular cases behave completely similar as the general case in Theorem 3.2, item (3), Equation (22). In the irregular case, only the bottom layer, consisting of the abelian quotient invariants of the derived subgroup, is exceptional and must be taken from ( [5] , Appendix 8, Thm. 8.8, p.461). □

3.2. Infinite IPAD Sequences

Now we come to the IPADs of pro- groups whose metabelianizations are members of infinite periodic sequences, inclusively mainlines, of coclass trees.

Theorem 3.2. (Second Main Theorem on, , and of large class)

Let be a pro-3 group having a transfer target type with top layer com- ponent. Let denote the defect of commutativity ( [9] , Section 3.1.1, p. 412, and Section 3.3.2, p. 429) of the metabelianization of. Then the ordered first layer and the bottom layer are given in the following way.

1) If is of coclass and nilpotency class, then

(19)

2) If is of coclass and nilpotency class, or c = 4 with, then

(20)

in dependence on the coclass tree, , but uniformly

(21)

3) If is of coclass and nilpotency class, or with, then

(22)

The first member of the ordered first layer reveals a uni-polarization (dependence on the nilpotency class), whereas the other three members, , show a stabilization (independence of) for fixed coclass.

Proof. Again, we make use of [5] , and we point out that, for a -group G, the index of nilpotency is used generally instead of the nilpotency class and the invariant frequently (but not always) replaces the coclass in that paper.

1) All components of are given in ([5] , Section 3.1, Thm. 3.1, Equation (3.4)-(3.5), p. 421) when their ordering is defined by the special selection of generators ([5] , Section 3.1, Equation (3.1)-(3.2), p. 420). There is only a unique coclass tree with 3-groups of coclass 1.

2) The first component of is given in ([5] , Section 3.2, Thm.3.2, Equation (3.7), p. 424), and the last three components of are given in ([5] , Section 4.5, Thm. 4.4, p. 440) and ([5] , Section 4.5, Tbl. 4.7, p. 441), when their ordering is defined by the special selection of generators ([5] , Section 3.2, Equation (3.6), p. 424). The invariant ([5] , Section 4, p. 426), which counts IPAD components of rank 3, decides to which of the mentioned three coclass trees the group belongs ( [9] , Figure 3.6-3.7, pp. 442-443).

3) The first two components of are given in ([5] , Section 3.2, Thm.3.2, Equation (3.7)-(3.8), p. 424), and the last two components of are given in ([5] , Section 4.6, Thm. 4.5, p. 444), when their ordering is defined by the special selection of generators ([5] , Section 3.2, Equation (3.6), p. 424). For coclass bigger than 2, it is irrelevant to which of the four (in the case of odd coclass) or six (in the case of even coclass) coclass trees the group belongs. The IPAD is independent of this detailed information, provided that.

Finally, the bottom layer, consisting of the abelian quotient invariants of the derived sub- group, is generally taken from ([5] , Appendix 8, Thm. 8.8, p. 461). □

4. Componentwise Correspondence of IPAD and TKT

Within this section, where generally, we employ some special terminology.

Definition 4.1. We say a class of a base field remains resistant if it does not capitulate in any unramified cyclic cubic extension.

When the 3-class group of is of type the next layer of unramified abelian extensions is already the top layer consisting of the Hilbert 3-class field, where a resistant class must capitulate, according to the Hilbert/Artin/Furtwängler principal ideal theorem [8] .

Our desire is to show that the components of the ordered IPAD and TKT [9] [19] are in a strict corre- spondence to each other. For this purpose, we exploit details of the proofs given in [5] , where generators of metabelian 3-groups G with were selected in a canonical way, particularly adequate for theore- tical aspects ([5] , Section 3.2, p. 424), ( [9] , Section 3.3.2, p. 429).

Since we now prefer a more computational aspect, we translate the results into a form which is given by the computational algebra system MAGMA [4] .

To be specific, we choose the vertices of two important coclass trees for illustrating these peculiar techniques. The vertices of depth (distance from the mainline) at most 1 of both coclass trees, with roots and ( [9] , Figure 3.6-3.7, pp. 442-443), are metabelian 3-groups with order, nilpotency class, and fixed coclass.

4.1. The Coclass Tree

Remark 4.1. The first layers of the TTT and TKT of vertices of depth at most 1 of the coclass tree ( [9] , Figure 3.6, p. 442) consist of four components each, and share the following common properties with respect to Magma’s selection of generators:

1) polarization (dependence on the class) at the first component of TTT and TKT,

2) Stabilization (independence of the class) at the last three components,

3) Rank 3 at the second TTT component (in [5] ).

Using the class, resp. an asterisk, as wildcard characters, these common properties can be summarized as follows, now including the details of the stabilization:

(23)

However, to assure the general applicability of the theorems and corollaries in this section, we aim at in- dependency of the selection of generators (and thus invariance under permutations).

Theorem 4.1. (in field theoretic terminology)

1) The class associated with the polarization becomes principal in the extension with rank 3.

2) The class associated with rank 3 becomes principal in both extensions of type, in particular, cannot be a permutation and can have at most one fixed point.

In the sequel, we use designations of special TKTs which were developed in [19] - [21] .

Remark 4.2. Aside from the common properties, there also arise variations due to the polarization, which we first express with respect to Magma’s selection of generators:

1) The TKT is E.6, , if and only if the polarized extension reveals a fixed point principa- lization.

2) The TKT is E.14, , if and only if one of the classes associated with type becomes principal in the polarized extension.

3) The TKT is H.4, , if and only if the class associated with rank 3 becomes principal in the polarized extension.

4) The TKT is c.18, , if and only if the polarized extension reveals a total principalization (indicated by 0).

Corollary 4.1. (in field theoretic terminology)

1) For the TKTs E.6 and H.4, both classes associated with type remain resistant, for TKT E.14 only one of them.

2) All extensions satisfy Taussky’s condition (B) [22] , with the single exception of the polarized extension in the case of TKT E.6 or c.18, which satisfies condition (A).

3) TKT E.6 has a single fixed point, E.14 contains a 3-cycle, and H.4 contains a 2-cycle.

Proof. (of Theorem 4.1 and Corollary 4.1)

Observe that in [5] , the index of nilpotency and the invariant are used rather than the nilpotency class and the coclass. The claims are a consequence of ([5] , 4.5, Tbl. 4.7, p. 441), when we perform a transformation from the first layer TKT and TTT

with respect to the canonical generators, to the corresponding invariants

with respect to Magma’s generators. □

4.2. The Coclass Tree

Remark 4.3. The first layer TTT and TKT of vertices of depth at most 1 of the coclass tree ( [9] , Figure 3.7, p. 443) consist of four components each, and share the following common properties with respect to Magma’s choice of generators:

1) polarization (dependence on the class) at the second component of TTT and TKT,

2) stabilization (independence of the class) at the other three components,

3) rank 3 does not occur at any TTT component (in [5] ).

Using the class, resp. an asterisk, as wildcard characters, the common properties can be summarized as follows, now including details of the stabilization:

(24)

Again, we have to ensure the general applicability of the following theorem and corollary, which must be in- dependent of the choice of generators (and thus invariant under permutations).

Theorem 4.2. (in field theoretic terminology)

1) Two extensions of type (21) reveal fixed point principalization satisfying condition (A) [22] .

2) The remaining extension of type (21) satisfies condition (B), since the class associated with the polarization becomes principal there.

Remark 4.4. Next, we come to variations caused by the polarization, which we now express with respect to Magma’s choice of generators:

1) The TKT is E.8, , if and only if the polarized extension reveals a fixed point principa- lization.

2) The TKT is E.9, , if and only if one of the classes associated with fixed points becomes principal in the polarized extension.

3) The TKT is G.16, , if and only if the class associated with type (21), satisfying con- dition (B), becomes principal in the polarized extension.

4) The TKT is c.21, , if and only if the polarized extension reveals a total principalization (indicated by 0).

Corollary 4.2. (in field theoretic terminology)

1) For the TKTs E.8 and E.9, the class associated with type (21), satisfying condition (B), remains resistant.

2) The polarized extension satisfies condition (B) [22] in the case of TKT E.9 or G.16, and it satisfies con- dition (A) in the case of TKT E.8 or c.21.

3) TKT G.16 is a permutation containing a 2-cycle, and TKT E.8 is the unique TKT possessing three fixed points.

Proof. (of Theorem 4.2 and Corollary 4.2)

In our paper [5] , the index of nilpotency and the invariant are used rather than the nil- potency class and the coclass. All claims are a consequence of ([5] , 4.5, Tbl. 4.7, p. 441), provided we perform a transformation from the first layer TKT and TTT

with respect to the canonical generators, to the corresponding invariants

with respect to Magma’s generators. □

5. Applications in Extreme Computing

5.1. Application 1: Sifting Malformed IPADs

Definition 5.1. An IPAD with bottom layer component is called malformed if it is not covered by Theorems 3.1 and 3.2.

To verify predicted asymptotic densities of maximal unramified pro-3 extensions in the article [10] numeri- cally, the IPADs of all complex quadratic fields with discriminants and 3-class rank were computed by Boston, Bush and Hajir with the aid of PARI/GP [1] . In particular, there occurred 276375, resp. 122444, such fields with 3-class group of type, resp..

Example 5.1.

A check of all 276375 IPADs for complex quadratic fields with type in the range of discriminants, for which Theorem 3.2 states that the 3-class groups of the 4 unramified cyclic cubic extensions can only have 3-rank 2, except for the unique type, revealed that the following 5 IPADs were com- puted erroneously by the used version of PARI/GP [1] in [10] . The successful recomputation was done with MAGMA [4] .

1) For d = −96174803, the erroneous IPAD contained the mal-

formed component instead of the correct. The transfer kernel type (TKT) [9] [19] [21] turned out to be F.12.

2) For, the erroneous IPAD contained the

malformed component instead of the correct. Its TKT is H.4.

3) For, the erroneous IPAD contained the mal-

formed component instead of the correct. The TKT is D.10.

4) For, the erroneous IPAD contained the mal-

formed component instead of the correct. This could be a TKT E.8 or E.9 or G.16.

5) For, the erroneous IPAD contained the

malformed component instead of the correct. This could be a TKT E.6 or E.14 or H.4.

For the last two cases, Magma failed to determine the TKT. Nevertheless, none of the discriminants

is particularly spectacular.

Example 5.2.

We also checked all 122444 IPADs for complex quadratic fields with type in the range of discriminants, Again, we found exactly 5 errors among these IPADs which had been computed by PARI/GP [1] in [10] . For the recomputation we used MAGMA [4] . The study of this extensive material was very helpful for the deeper understanding of 3-groups having abelianization of type. Systematic results in the style of Theorems 3.1 and 3.2 will be given in a forthcoming paper. The abbreviation pTKT means the punctured TKT.

1) For, the erroneous IPAD contained

the malformed component instead of the correct. This could be a homocyclic pTKT B.2 or C.4 or D.5.

2) For d = −79749087, the erroneous IPAD contained the mal-

formed component instead of the correct. It is a pTKT D.11,.

3) For, the erroneous IPAD contained

the malformed component instead of the correct. It could be a homocyclic pTKT B.2 or C.4 or D.5.

4) For, the erroneous IPAD contained the

malformed component instead of the correct. This could be a pTKT B.2 or C.4 or D.5 in the first excited state.

5) For d = −86139199, the erroneous IPAD contained the mal-

formed component instead of the correct. This is clearly a pTKT D.11,.

Again, none of the corresponding discriminants

is particularly spectacular.

We emphasize that, in both Examples 5.1 and 5.2, the errors of PARI/GP [1] occured in the upper limit range of absolute discriminants above 70 millions. This seems to be a critical region of extreme computing where current computational algebra systems become unstable. MAGMA [4] also often fails to compute the TKT in that range.

Fortunately, there appeared a single discriminant only for each of the 5 erroneous IPADs, in both examples. This indicates that the errors are not systematic but rather stochastic.

5.2. Application 2: Completing Partial Capitulation Types

Example 5.3. For the discriminant of the complex quadratic field with 3-class

group of type, we constructed the four unramified cyclic cubic extensions, , and com-

puted the IPAD with the aid of MAGMA [4] .

According to Equation (20) in Theorem 3.2, the second 3-class group G of K must be of coclass, and the polarized component 54 of the IPAD shows that and thus the nilpotency class and the defect of commutativity are given by either, , or,. Further, in view of the rank-3 component of the IPAD, must be a vertex of the coclass tree.

When we tried to determine the 3-principalization type, Magma succeeded in calculating and but unfortunately failed to give and. With respect to the complete IPAD, Theorem 4.1 enforces (item (1)) and (item (2)), and therefore the partial result is completed to. According to item (3) of Remark 4.2 or item (3) of Corollary 4.1, is of TKT H.4. Our experience suggests that this TKT compels the arrangement, , expressed by the weak leaf conjecture ( [9] , Cnj. 3.1, p. 423).

Example 5.4. For the discriminant of the complex quadratic field with 3-class

group of type, we constructed the four unramified cyclic cubic extensions, , and com-

puted the IPAD with the aid of MAGMA [4] .

According to Equation (20) in Theorem 3.2, the second 3-class group of must be of coclass, and the polarized component 54 of the IPAD shows that and thus the nilpotency class and the defect of commutativity are given by either, , or,. Further, due to the lack of a rank-3 component in the IPAD, must be a vertex of the coclass tree.

Next, we tried to determine the 3-principalization type. Magma succeeded in calculating two fixed points and but unfortunately failed to give and. With respect to the complete IPAD, Theorem 4.2 enforces or (item (1)), and or (item (2)), and therefore the partial result is completed to or. According to item (1) of Remark 4.4 or item (3) of Corollary 4.2, is of TKT E.8, and this TKT enforces the arrangement, , since is impossible.

Example 5.5. For the discriminant of the complex quadratic field with 3-

class group of type, we constructed the four unramified cyclic cubic extensions, , and

computed the IPAD with the aid of MAGMA [4] .

According to Equation (20) in Theorem 3.2, the second 3-class group G of K must be of coclass, and the polarized component 65 of the IPAD shows that and thus the nilpotency class and the defect of commutativity are given by either, , or,. Further, in view of the rank-3 component of the IPAD, must be a vertex of the coclass tree.

Then we tried to determine the 3-principalization type. Magma succeeded in calculating and but unfortunately failed to give and. With respect to the complete IPAD, Theorem 4.1 enforces and (item (2)), whereas the claim in item (1) is confirmed, and therefore the partial result is completed to. According to item (2) of Remark 4.2 or item (3) of Corollary 4.1, is of TKT E.14, and this TKT enforces the arrangement, , since is impossible.

6. Iterated IPADs of Second Order

In this section, where generally, we apply iterated IPADs of second order for indirectly computing - capitulation types in Section 6.1 and finding the exact length of -class towers in Section 6.2.

6.1. p-Capitulation Type

By means of the following theorem, the exact 3-principalization type [9] [19] [21] of real quadratic fields

, , can be determined indirectly with the aid of information on the structure of 3-class groups

of number fields of absolute degree.

Theorem 6.1. (Indirect computation of the -capitulation type)

Suppose that and let be a number field with 3-class group of type and 3-tower group.

1) If the IPAD of is given by

then by Equation (14) in Theorem 3.1,

in particular, the length of the 3-class tower of is given by.

2) If the first layer of abelian unramified extensions of consists of, then the iterated IPAD of second order

admits a sharp decision about the group and the first layer of the transfer kernel type

(25)

if and only if, and thus.

(26)

if and only if, and thus.

(27)

if and only if, and thus.

Proof. It suffices to compute the iterated IPADs of the groups with the aid of MAGMA [4] , simply by investigating their four maximal normal subgroups,. □

Example 6.1. A possible future application of Theorem 6.1 could be, for instance, the separation of the capitulation types a.2, , and a.3, , among the 1386 real quadratic fields

, , with 3-class group of type and IPAD,

which was outside of our reach in all investigations of ( [23] , Tbl. 2, p. 496), ( [5] , Tbl. 6.1, p. 451) and ( [9] , Figure 3.2, p. 422). The reason why we expect this enterprise to be promising is that our experience with MAGMA [4] shows that computing class groups can become slow but remains sound and stable for huge discriminants, whereas the calculation of capitulation kernels frequently fails.

6.2. Length of the p-Class Tower

In this section, we use the iterated IPAD of second order for the

indirect computation of the length of the -class tower of a number field with -tower group, where denotes a fixed prime.

We begin with theorems which permit a decision between finitely many possibilities for the length in Section 6.2.1. These results systematically extend the investigations of complex quadratic fields in [6] to arbitrary base fields and yield the first examples of real quadratic fields having a -class tower of exact length three. Then, in Section 6.2.3, we launch the first successful attack against quadratic fields whose second -class group possesses an infinite cover ( [16] , Dfn.21.2), and for which the problem of finding the length was completely unsolved up to now [13] . In Section 6.2.2, some prerequisites con- cerning periodic bifurcations are provided.

6.2.1. Second p-Class Groups with Finite Cover

In the following theorems, we must use extended identifiers [4] [24] [25] of finite 3-groups with order bigger than, which lie outside of the SmallGroups database [17] [18] . This was explained in ( [16] , Section 9).

Theorem 6.2. (Length of the 3-class tower for)

Suppose that and let be a number field with 3-class group of type and 3-tower group.

1) If the IPAD of is given by

and the first layer TKT neither contains a total principalization nor a 2-cycle, then there are two possi- bilities for the length of the 3-class tower of.

2) If the first layer of abelian unramified extensions of consists of, then the iterated IPAD of second order

admits a sharp decision about the length.

(28)

if and only if, and thus.

(29)

if and only if, and thus.

Proof. According to Theorem 3.2, an IPAD of the form indicates that the

metabelianization of the group belongs to the coclass tree ( [9] , Figure 3.6, p. 442) and has nilpotency class, due to the polarization.

According to Section 4.1, the lack of a total principalization excludes the TKT c.18 and the absence of a 2-cycle discourages the TKT H.4, whence the group must be of TKT E.6 or E.14.

By means of the techniques described in ( [6] , Proof of Thm. 4.1), a search in the complete descendant tree, not restricted to groups of coclass 2, yields exactly six candidates for the group G: three metabe- lian groups with, and three groups of derived length 3 and order with gene- ralized identifiers . There cannot exist adequate groups of bigger orders ( [6] , Cor. 3.0.1). The former three groups are charcterized by Equations (28) the latter three groups (see [16] , 21.2, Figure 8) by Equations (29).

Finally, we have. □

Theorem 6.3. (Length of the 3-class tower for)

Suppose that and let be a number field with 3-class group of type and 3-tower group.

1) If the IPAD of is given by

and the first layer TKT neither contains a total principalization nor a 2-cycle, then there are two possi- bilities for the length of the 3-class tower of.

2) If the first layer of abelian unramified extensions of consists of, then the iterated IPAD of second order

admits a sharp decision about the length.

(30)

if and only if, and thus.

(31)

if and only if, and thus.

Proof. According to Theorem 3.2, an IPAD of the form indicates that the metabe-

lianization of the group belongs to the coclass tree ( [9] , Figure 3.7, p. 443) and has nil- potency class, due to the polarization.

According to Section 4.2, the lack of a total principalization excludes the TKT c.21 and the absence of a 2-cycle discourages the TKT G.16, whence the group must be of TKT E.8 or E.9.

As we have shown in detail in [6] , Proof of Thm. 4.1], a search in the complete descendant tree, not restricted to groups of coclass 2, yields exactly six candidates for the group: three metabelian groups with, and three groups of derived length 3 and order with generalized identifiers . There cannot exist adequate groups of bigger orders ([6] , Cor. 3.0.1). The former three groups are characterized by Equations (30) the latter three groups (see [16] , Section 21.2, Figure 9) by Equations (31).

Eventually, the 3-tower length of, , coincides with the derived length of. □

Example 6.2. (The first real quadratic field with.) In June 2006, we discovered the smallest

discriminant of a real quadratic field with 3-class group of type whose

3-tower group possesses the transfer kernel type E.9, ([19] , Tbl. 4, p. 498).

The complex quadratic analogue was known since 1934 by the famous paper of Scholz and

Taussky [20] . However, it required almost 80 years until M.R. Bush and ourselves ([6] , Cor. 4.1.1) succeeded in providing the first faultless proof that has a 3-class tower of exact length with -tower group isomorphic to one of the two Schur -groups of order.

For, the methods in [6] do not admit a final decision about the length. They only

yield four possible 3-tower groups of K, namely either the two unbalanced groups with and relation rank bigger than the generator rank or the two Schur -groups with and equal to.

In October 2014, we succeeded in proving that three of the unramified cyclic cubic extensions reveal

the critical IPAD component in Equation (31) of Theorem 6.3, item (2), whence also

and. This was done by computing 3-class groups of number fields of ab- solute degree 6 × 3 = 18 with the aid of MAGMA [4] .

6.2.2. Another Descendant Tree with Periodic Bifurcations

In ( [16] , Section 21.2), we provided computational evidence of periodic bifurcations in pruned descendant trees with roots. Now we want to show that the immediate descendant of another root possesses an infinite balanced cover ( [16] , Dfn. 21.2). For this purpose we construct an extensive finite part of the descendant tree with the aid of MAGMA [4] and we combine the gained insight with results of L. Bartholdi and M.R. Bush [13] . The group has been called the non-CF group by J. Ascione, G. Havas and C.R. Leedham-Green [26] [27] .

For brevity, we give 3-logarithms of abelian type invariants in the following theorem and we denote iteration

by formal exponents, for instance, , , , and we eliminate

initial anomalies of generalized identifiers by putting

, for, formally. (Observe that actually

, whereas.)

Theorem 6.4. Let be a positive integer bounded from above by 8.

1) In the descendant tree of, there exists a unique path with length of -groups ( [16] , Dfn. 10.1),

and (reverse) directed edges with alternating step sizes 1 and 2 such that, for all (is a section of the surjection on this path), and all the vertices with even superscript i = 2j, ,

(32)

resp. all the vertices with odd superscript ,

(33)

of this path share the following common invariants, respectively:

-the uniform IPAD

(34)

-the uniform transfer kernel type

(35)

-the 3-multiplicator rank and the nuclear rank [14] [16] ,

(36)

resp., giving rise to the bifurcations for odd,

(37)

-and the counters of immediate descendants [16] [18] ,

(38)

resp.

(39)

determining the local structure of the descendant tree.

2) A few other invariants of the vertices depend on the superscript,

-the 3-logarithm of the order, the nilpotency class and the coclass,

(40)

resp.

(41)

Theorem 6.4 provides the scaffold of the pruned descendant tree of with the dis- tinguished path and periodic bifurcations.

With respect to our intended applications, however, the following Corollaries 6.1 and 6.2 are of the greatest importance.

Corollary 6.1. Let be a non-negative integer, where.

Whereas the vertices with even superscript, , that is, , are merely links in the distinguished path, the vertices with odd superscript , that is,

, reveal the essential periodic bifurcations with the following properties.

1) The regular component of the descendant tree is a finite tree which contains the root and four terminal -groups,

2) The irregular component of the descendant tree is a forest which con- tains a single isolated Schur -group

and additionally contains the next vertex of the distinguished path.

Remark 6.1. We apply a sifting strategy for reducing the entire descendant tree to a pruned des- cendant tree by filtering all vertices which are -groups. The process consists of

1) keeping the unique terminal step size-2 descendant, which is exactly the Schur -group, the unique capable step size-2 descendant, and the 4 terminal step size-1 descendants, , which are - groups, of, , and

2) eliminating ([16] , Section 20, (F1)) the 3 non- groups, together with their complete descendant trees, among the 4capable step size-1 descendants of,.

A finite part at the top of the resulting tree is drawn in Figure 1.

Proof. (of Theorem 6.4, and Corollary 6.1)

The -group generation algorithm [28] [29] , which is implemented in the computational algebra system MAGMA [2] - [4] , was used for constructing the pruned descendant tree with root which was defined as the disjoint union of all regular components, i.e. finite trees

with the descendants, , of as roots, together with 2siblings in the irregular component

one of them the Schur -group with 3-multiplicator rank and nuclear rank, the other the next vertex of the distinguished path.

The vertical construction was terminated for at nilpotency class 2 × 8 + 3 = 19. The horizontal construction was extended up to coclass, where the consumption of CPU time became annoying. □

The extent to which we constructed the pruned descendant tree suggests the following con- jecture.

Conjecture 6.1. Theorem 6.4 and Corollary 6.1 remain true for an arbitrarily large positive integer, not necessarily bounded by 8.

For the convenience of the reader, we now recall ( [16] , Dfn. 21.2):

Definition 6.1. Let be a finite metabelian -group, then the set of all finite non-metabelian -groups whose second derived quotient is isomorphic to is called the cover of. The subset consisting of Schur -groups in is called the balanced cover of.

Corollary 6.2. The group, which does not have a balanced presentation, has an infinite cover and even an infinite balanced cover. More precisely, the covers are given explicitly by

(42)

For the proof, we have to recall that L. Bartholdi and M.R. Bush ( [13] , Thm. 2.1, p. 160, and Prop. 3.6, p. 165) have constructed an infinite family of Schur -groups with strictly increasing 3-power order, nil- potency class, coclass, and increasing unbounded derived length

Figure 1. Periodic bifurcations in the pruned descendant tree.

(43)

such that is the well-known metabelian two-stage tower group of the complex qua-

dratic field ( [9] , Thm. 1.5, p. 407), ( [20] , pp. 22-25), ( [30] , p. 20) with IPAD

. All the other members of the family with are non-metabelian and share

the common IPAD.

Proof. Several issues must be clarified for the groups with.

Firstly, according to the Equations (15) and (16) in Theorem 3.1, there are only five possibilities for the metabelianizations, namely the groups and. However, we can eliminate, because it has an empty cover by ( [9] , Thm. 1.4, p. 406). We can also cancel by ([6] , Lem. 3.3), since they fail to be -groups. In fact, the same arguments as for the apply to all vertices of the pruned tree, since they are -groups, by definition. This shows that

(44)

Secondly, we have to make sure that the , and more generally all finite 3-groups with IPAD

, are descendants of. Since the abelian 3-group with type invariants 21 is not a quotient

of, ([6] , Cor. 3.0.1) shows that such a group cannot be descendant of any other sibling with of, which contains at least two maximal subgroups of type 21. According to Equation (14) in Theorem 3.1, the unique remaining possibility for an ancestor having the required IPAD

is the extra special group. However, this group has been exhausted completely already,

since it gives rise to exactly the seven immediate step size-2 descendants with, mentioned above.

Finally, the Schur -groups G_n must necessarily coincide with the periodic sequence of Schur -groups, whose initial sections were constructed in Corollary 6.1, and which must be continued in- ductively in the sense of Conjecture 6.1:

(45)

Indeed, since each is a sibling of, for, having identical invariants, Equation (40) in Theorem 6.4 shows that all invariants of coincide with those of

(46)

Consequently, the inclusions in Equation (44) can be replaced by equalities, and the claims of Corollary 6.2 are proved. □

Remark 6.2.

1) The claims of Conjecture 6.1 are strongly supported by the proven infinitude of the family of Schur -groups in [13] and their obvious coincidence with the periodic sequence in Corollary 6.1.

2) The IPAD is a considerably more restrictive condition for a pro-3 group than the TKT

H.4, , which is necessarily the TKT of all descendants of , by ( [6] , Cor.3.0.2). However, the TKT H.4 is unable to characterize the vertices of the tree of uniquely, since there are lots of vertices with TKT H.4 in the tree of , and, as we have seen in Remark 4.2, the same is true for the tree of , since and are equivalent ( [21] , Section 3, p. 79).

3) The exact specification of the infinite cover, resp. the infinite and entirely non-metabelian balanced cover, of in Corollary 6.2 implies that the length of the 3-class tower of a real, resp. complex,

quadratic field with IPAD can take any value bigger than 1, resp. 2, or even

. In the complex case, the 3-tower group must be a Schur -group, according to [6] [10] [31] [32] .

6.2.3. Second p-Class Groups with Infinite Cover

As a final coronation of this section, we show that our new IPAD strategies are powerful enough to enable the

determination of the length for some quadratic fields with IPAD

with the aid of information on the structure of 3-class groups of number fields of ab-

solute degree. This is close to the limits of what can currently be done with MAGMA [4] on powerful machines.

For this purpose, we extend the concept of iterated IPADs of second order

once more by adding the second layers to all IPADs of unramified degree- extensions. The resulting iterated multi-layered IPAD of second order is indicated by an asterisk

Theorem 6.5. (Length of the 3-class tower for)

Suppose that and let be a quadratic number field with 3-class group of type and 3-tower group.

1) If the IPAD of is given by

then the first layer TKT is and there exist infinitely many possibilities for the length of the 3-class tower of.

2) If the first layer of abelian unramified extensions of consists of, then the iterated multi-layered IPAD of second order

admits certain partial decisions about the length as follows.

(47)

if and only if, and thus.

(48)

if and only if, and thus.

(49)

if and only if, and thus.

(50)

if and only if either or, and thus.

(51)

if and only if, and thus.

(52)

if and only if either or, both of order 3⁸, and thus.

(53)

occurs for of order, where.

(54)

occurs for either

or

or, all of order, where.

(55)

occurs for of order, where.

(56)

occurs for either

, , of order, where,

or of order, where.

The various groups which occur in Theorem 6.5 are drawn in the tree diagram of Figure 1. This diagram im- pressively visualizes periodically repeating bifurcations in the descendant tree of Ascione’s non-CF group. An essential difference to the trees and in ([16] , Section 21.2), where and, is that the regular component of each vertex with coclass and nuclear rank, giving rise to a bifurcation, is not a coclass tree but rather a finite tree with root and four terminal immediate descendants. The irregular component is a forest containing an isolated Schur -group and the parent of the next vertex with bifurcation (together with its regular com- ponent).

Proof. If we restricted the statements to complex quadratic fields it would be sufficient to consider the Schur -groups, , in the descendant tree. But since we are also interested in the behaviour of real quadratic fields, we must determine the iterated multi-layered IPADs of second order of all vertices in the pruned descendant tree consisting of -groups. We do this for the groups up to the order 3¹⁷, which were constructed in Section 6.2.2, by investigating their four maximal normal subgroups, , with the aid of MAGMA [4] . Finally, we make use of the relation. □

We point out that Equation (56) cannot be used for a conclusive identification.

Example 6.3. (The first quadratic fields with TKT H.4 and) In December 2009, we discovered

the smallest discriminant of a real quadratic field with 3-class group of type

whose 3-tower group possesses the transfer kernel type H.4, ([19] , Tbl. 4, p. 498). In January 2010, we found two further examples.

The complex quadratic analogue was known since 1982 by the paper of Heider and Schmithals ( [30] , p. 20), whereas Scholz and Taussky gave an erroneous TKT F.7, ( [20] , Footnote, p. 36). There is another example in ( [30] , Tbl. 3, p. 19) and in November 1989, we found

([21] , p. 84). All these fields share the same IPAD.

In February 2015, we succeeded in proving that the unramified cyclic cubic extensions, for , resp., resp., reveal the critical first and second layer IPAD components in Equation (52), resp. (56), resp. (51), of Theorem 6.5, item (2), whence cer- tainly, for all these fields, with the single exception of, where also could be possible.

However, the 3-class tower groups of are different: for we have the Schur -group of order, and for we have the unbalanced group, which is distinguished by possessing three pairwise non-isomorphic maximal sub- groups of type. For, the group remains unknown.

The justifications were conducted by computing 3-class groups of number fields of absolute degree 6 × 9 = 54 with the aid of MAGMA [4] on a machine with two XEON 8-core CPUs and 256 GB RAM.

7. Complex Quadratic Fields of 3-Rank Three

In this concluding section we present another intriguing application of IPADs.

Due to Koch and Venkov [32] , it is known that a complex quadratic field with 3-class rank has an infinite 3-class field tower of length. In the time between 1973 and 1978, Diaz y Diaz [33] [34] and Buell [35] have determined the smallest absolute discri- minants of such fields. Recently, we have launched a computational project which aims at verifying these classical results and adding sophisticated arithmetical details. Below the bound there exist 25 discri- minants of this kind, and 14 of the corresponding fields have a 3-class group of elementary abelian type. For each of these 14 fields, we determine the type of 3-principalization in the thirteen unramified cyclic cubic extensions of, and the structure of the 3-class groups of these extensions, i.e., the IPAD of K. We characterize the metabelian Galois group of the second Hilbert 3-class field by means of kernels and targets of its Artin transfer homomorphisms [8] to maximal subgroups. We provide evidence of a wealth of structure in the set of infinite topological 3-class field tower groups by showing that the 14 groups are pairwise non-isomorphic.

We summarize our results and their obvious conclusion in the following theorem.

Theorem 7.1.

There exist exactly 14 complex quadratic number fields with 3-class groups of type and discriminants in the range. They have pairwise non-isomorphic

1) second and higher 3-class groups, ,

2) infinite topological 3-class field tower groups.

Before we come to the proof of Theorem 7.1 in Section 7.3, we collect basic numerical data concerning fields with in Section 7.1, and we completely determine sophisticated arithmetical invariants in Section 7.2 for all fields with of type. The first attempt to do so for the smallest absolute discri- minant with is due to Heider and Schmithals in ( [30] , Section 4, Tbl. 2, p. 18), but it resulted in partial success only.

7.1. Discriminants of Fields with Rank

Since one of our aims is to investigate tendencies for the coclass of second and higher -class groups

, , [9] [23] of a series of algebraic number fields with infinite -class

field tower, for an odd prime, the most obvious choice which suggests itself is to take the smallest

possible prime and to select complex quadratic fields, , having the simplest possi-

ble 3-class group of rank 3, that is, of elementary abelian type.

The reason is that Koch and Venkov [32] have improved the lower bound of Golod, Shafarevich [31] [36] and Vinberg [37] for the -class rank, which ensures an infinite -class tower of a complex quadratic field, from 4 to 3.

However, quadratic fields with 3-rank are sparse. Diaz y Diaz and Buell [33] - [35] [38] have determined the minimal absolute discriminant of such fields to be.

To provide an independent verification, we used the computational algebra system MAGMA [2] - [4] for compiling a list of all quadratic fundamental discriminants of fields with 3-class rank. In 16 hours of CPU time we obtained the 25 desired discriminants and the abelian type in- variants (here written in 3-power form) of the corresponding 3-class groups, and also of the complete class groups, as given in Table 1. There appeared only one discriminant (No. 16) which is not contained in ( [34] , Appendix 1, p.68) already.

There are 14 discriminants, starting with, such that is elementary abelian of type

Table 1. Data collection for and.

, and 10 discriminants, starting with, such that is of non-elementary type. For the single discriminant, we have a 3-class group of type. We have published this information in the Online Encyclopedia of Integer Sequences (OEIS) [39] , sequences A244574 and A244575.

7.2. Arithmetic Invariants of Fields with

After the preliminary data collection in Section 7.1, we restrict ourselves to the 14 cases with elementary abe-

lian 3-class group of type. The complex quadratic field possesses 13 unramified cyclic

cubic extensions with dihedral absolute Galois group of order six [23] . Based on Fieker’s technique [40] , we use the computational algebra system MAGMA [3] [4] to construct these extensions and to calculate their arithmetical invariants. In Table 2, which is continued in Table 3 on the following page, we present the kernel of the 3-principalization of in [21] [23] , the occupation numbers of the principalization kernels [19] , and the abelian type invariants, resp., of the 3-class group, resp., for each [5] [9] . Here, we denote by the unique real non-Galois absolutely

Table 2. Pattern recognition via ordered IPADs.

Table 3. Pattern recognition (continued).

cubic subfield of. For brevity, we give 3-logarithms of abelian type invariants and we denote iteration by formal exponents. Note that the multiplets and are ordered and in componentwise mutual correspon- dence, in the sense of 4.

In Table 4, we classify each of the 14 complex quadratic fields of type according to

the counters of the abelian type invariants of the 3-class groups of the 13 unramified cyclic cubic extensions, that is the accumulated (unordered) form of the IPAD of. Whereas the dominant part of these groups is of order, there always exist(s) at least one and at most four distinguished groups of bigger order, usually and occasionally even. According to the number of distinguished groups, we speak about uni-, bi-, tri- or tetra-polarization. If the maximal value of the order is, then we have a ground state, otherwise an excited state.

7.3. Proof of Theorem 7.1

Proof. According to ( [9] , Thm.1.1 and Dfn. 1.1, pp. 402-403), the information given in Table 4 consists of iso- morphism invariants of the metabelian Galois group of the second Hilbert 3-class field of [23] . Consequently, with respect to the 13 abelian type invariants of the 3-class groups alone, only the groups for could be isomorphic. However, Table 2 and Table 3 show that these three groups differ with respect to another isomorphism invariant, the 3-principalization type [19] [21] , since the corresponding maximal occupation numbers of the multiplet are, respectively. □

7.4. Final Remark

We would like to emphasize that Theorem 7.1 provides evidence of a wealth of structure in the set of infinite 3-class field towers, which was unknown up to now, since the common practice is to consider a 3-class field tower as done when some criterion in the style of Golod-Shafarevich-Vinberg [31] [36] [37] or Koch-Venkov [32] ensures just its infinity. However, this perspective is very coarse and our result proves that it can be refined considerably.

It would be interesting to extend the range of discriminants and to find the first examples of isomorphic infinite 3-class field towers.

Table 4. Accumulative (unordered) form of IPADs.

Another very difficult remaining open problem is the actual identification of the metabelianizations of the 3-tower groups of the 14 fields. The complexity of this task is due to unmanageable descendant numbers of certain vertices, e.g. and, in the tree with root.

Acknowledgements

We gratefully acknowledge that our research is supported by the Austrian Science Fund (FWF): P 26008-N25. The results of this paper will be presented during the 29th Journées Arithmeétiques at the University of Debrecen [41] .

Funding

Research supported by the Austrian Science Fund (FWF): P 26008-N25.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	The PARI Group (2014) PARI/GP. Version 2.7.2, Bordeaux. http://pari.math.u-bordeaux.fr
[2]	Bosma, W., Cannon, J. and Playoust, C. (1997) The Magma Algebra System I: The User Language. Journal of Symbolic Computation, 24, 235-265. http://dx.doi.org/10.1006/jsco.1996.0125
[3]	Bosma, W., Cannon, J.J., Fieker, C. and Steels, A., Eds. (2015) Handbook of Magma Functions. Edition 2.21, University of Sydney, Sydney.
[4]	The MAGMA Group (2015) MAGMA Computational Algebra System. Version 2.21-2, Sydney. http://magma.maths.usyd.edu.au
[5]	Mayer, D.C. (2014) Principalization Algorithm via Class Group Structure. Journal de Théorie des Nombres de Bordeaux, 26, 415-464.
[6]	Bush, M.R. and Mayer, D.C. (2015) 3-Class Field Towers of Exact Length 3. Journal of Number Theory, 147, 766-777. http://arxiv.org/abs/1312.0251
[7]	Artin, E. (1927) Beweis des allgemeinen Reziprozitatsgesetzes. Abhandlungen aus dem Mathematischen Seminar der Universitat Hamburg, 5, 353-363. http://dx.doi.org/10.1007/BF02952531
[8]	Artin, E. (1929) Idealklassen in Oberkorpern und allgemeines Reziprozitatsgesetz. Abhandlungen aus dem Mathematischen Seminar der Universitat Hamburg, 7, 46-51. http://dx.doi.org/10.1007/BF02941159
[9]	Mayer, D.C. (2013) The Distribution of Second p-Class Groups on Coclass Graphs. Journal de Théorie des Nombres de Bordeaux, 25, 401-456. http://dx.doi.org/10.5802/jtnb.842
[10]	Boston, N., Bush, M.R. and Hajir, F. (2014) Heuristics for p-Class Towers of Imaginary Quadratic Fields, with an Appendix by Jonathan Blackhurst. Mathematische Annalen, in Press. http://arxiv.org/abs/1111.4679
[11]	Boston, N. and Leedham-Green, C. (2002) Explicit Computation of Galois p-Groups Unramified at p. Journal of Algebra, 256, 402-413. http://dx.doi.org/10.1016/S0021-8693(02)00028-5
[12]	Bush, M.R. (2003) Computation of Galois Groups Associated to the 2-Class Towers of Some Quadratic Fields. Journal of Number Theory, 100, 313-325. http://dx.doi.org/10.1016/S0022-314X(02)00128-2
[13]	Bartholdi, L. and Bush, M.R. (2007) Maximal Unramified 3-Extensions of Imaginary Quadratic Fields and SL2(Z3). Journal of Number Theory, 124, 159-166. http://dx.doi.org/10.1016/j.jnt.2006.08.008
[14]	Boston, N. and Nover, H. (2006) Computing Pro-p Galois Groups. Proceedings of ANTS 2006, Lecture Notes in Computer Science 4076, Springer-Verlag Berlin Heidelberg, Berlin, 1-10.
[15]	Nover, H. (2009) Computation of Galois Groups of 2-Class Towers. Ph.D. Thesis, University of Wisconsin, Madison.
[16]	Mayer, D.C. (2015) Periodic Bifurcations in Descendant Trees of Finite p-Groups. Advances in Pure Mathematics, 5, 162-195. http://dx.doi.org/10.4236/apm.2015.54020
[17]	Besche, H.U., Eick, B. and O’Brien, E.A. (2002) A Millennium Project: Constructing Small Groups. International Journal of Algebra and Computation, 12, 623-644. http://dx.doi.org/10.1142/S0218196702001115
[18]	Besche, H.U., Eick, B. and O’Brien, E.A. (2005) The Small Groups Library—A Library of Groups of Small Order. An Accepted and Refereed GAP 4 Package, Available Also in MAGMA.
[19]	Mayer, D.C. (2012) Transfers of Metabelian p-Groups. Monatshefte für Mathematik, 166, 467-495.
[20]	Scholz, A. and Taussky, O. (1934) Die Hauptideale der kubischen Klassenkorper imaginar quadratischer Zahlkorper: Ihre rechnerische Bestimmung und ihr Einflub auf den Klassenkorperturm. Journal für die Reine und Angewandte Mathematik, 171, 19-41.
[21]	Mayer, D.C. (1990) Principalization in Complex S3-Fields. Congressus Numerantium, 80, 73-87.
[22]	Taussky, O. (1970) A Remark Concerning Hilbert’s Theorem 94. Journal für die Reine und Angewandte Mathematik, 239/240, 435-438.
[23]	Mayer, D.C. (2012) The Second p-Class Group of a Number Field. International Journal of Number Theory, 8, 471-505.
[24]	Gamble, G., Nickel, W. and O’Brien, E.A. (2006) ANU p-Quotient—p-Quotient and p-Group Generation Algorithms. An Accepted GAP 4 Package, Available Also in MAGMA.
[25]	The GAP Group (2015) GAP—Groups, Algorithms, and Programming—A System for Computational Discrete Algebra. Version 4.7.7, Aachen, Braunschweig, Fort Collins, St. Andrews. http://www.gap-system.org
[26]	Ascione, J.A., Havas, G. and Leedham-Green, C.R. (1977) A Computer Aided Classification of Certain Groups of Prime Power Order. Bulletin of the Australian Mathematical Society, 17, 257-274, Corrigendum 317-319, Microfiche Supplement, 320.
[27]	Ascione, J.A. (1979) On 3-Groups of Second Maximal Class. Ph.D. Thesis, Australian National University, Canberra.
[28]	O’Brien, E.A. (1990) The p-Group Generation Algorithm. Journal of Symbolic Computation, 9, 677-698. http://dx.doi.org/10.1016/S0747-7171(08)80082-X
[29]	Holt, D.F., Eick, B. and O’Brien, E.A. (2005) Handbook of Computational Group Theory. Discrete Mathematics and Its Applications, Chapman and Hall/CRC Press. http://dx.doi.org/10.1201/9781420035216
[30]	Heider, F.-P. and Schmithals, B. (1982) Zur Kapitulation der Idealklassen in unverzweigten primzyklischen Erweiterungen. Journal für die reine und angewandte Mathematik, 336, 1-25.
[31]	Shafarevich, I.R. (1966) Extensions with Prescribed Ramification Points. Publications mathématiques de l’IHéS, 18, 71-95.
[32]	Koch, H. and Venkov, B.B. (1975) über den p-Klassenkorperturm eines imaginar-quadratischen Zahlkorpers. Astérisque, 24-25, 57-67.
[33]	Diaz, F. and Diaz (1973/74) Sur les corps quadratiques imaginaires dont le 3-rang du groupe des classes est supérieur à 1. Séminaire Delange-Pisot-Poitou, No. G15.
[34]	Diaz, F. and Diaz (1978) Sur le 3-rang des corps quadratiques. No. 78-11, Université Paris-Sud, Orsay.
[35]	Buell, D.A. (1976) Class Groups of Quadratic Fields. Mathematics of Computation, 30, 610-623.
[36]	Golod, E.S. and Shafarevich, I.R. (1965) On Class Field Towers. Izvestiya Akademii Nauk SSSR. Seriya Matematicheskaya, 28, 261-272.
[37]	Vinberg, E.B. (1965) On a Theorem Concerning the Infinite-Dimensionality of an Associative Algebra. Izvestiya Akademii Nauk SSSR. Seriya Matematicheskaya, 29, 209-214.
[38]	Shanks, D. (1976) Class Groups of the Quadratic Fields Found by Diaz y Diaz. Mathematics of Computation, 30, 173-178. http://dx.doi.org/10.1090/S0025-5718-1976-0399039-9
[39]	Sloane, N.J.A. (2014) The On-Line Encyclopedia of Integer Sequences (OEIS). The OEIS Foundation Inc. http://oeis.org/
[40]	Fieker, C. (2001) Computing Class Fields via the Artin Map. Mathematics of Computation, 70, 1293-1303.
[41]	Mayer, D.C. (2015) Index-p Abelianization Data of p-Class Tower Groups. Proceedings of the 29th Journées Arithmé-tiques, Debrecen, 6-10 July 2015, in Preparation.