Bell’s Ternary Quadratic Forms and Tunnel’s Congruent Number Criterion Revisited ()
1. Introduction
A seminal breakthrough in the theory of numbers is the determination by Gauss [1] of the number of representations 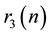 of an integer n as a sum of three squares
of an integer n as a sum of three squares 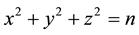 counting zeros, permutations and sign changes (e.g. Dickson [2] , Preface, pp. ix, x). A very explicit modern expression for this counting function is given in Cooper and Hirschhorn [3] , Lemma 4, Equation (3.1), and Theorem 3, Equation (1.27), (1.28). Note that the latter result has only been obtained quite recently by Hirschhorn and Sellers [4] .
counting zeros, permutations and sign changes (e.g. Dickson [2] , Preface, pp. ix, x). A very explicit modern expression for this counting function is given in Cooper and Hirschhorn [3] , Lemma 4, Equation (3.1), and Theorem 3, Equation (1.27), (1.28). Note that the latter result has only been obtained quite recently by Hirschhorn and Sellers [4] .
More generally, given a ternary (diagonal) quadratic form , one is interested in the total number
, one is interested in the total number 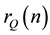 of integer solutions of the Diophantine equation
of integer solutions of the Diophantine equation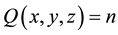 . This number is also
. This number is also
denoted by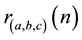 . By the time of Dickson’s monumental “History of the Theory of Numbers”, only few
. By the time of Dickson’s monumental “History of the Theory of Numbers”, only few
specific results are known for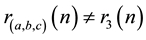 . Bell [5] mentions an unproven result by Liouville and incomplete results by Torelli and Stieltjes (see Dickson [2] , pp. 294, 295, and Dickson [6] , pp. 133, 216).
. Bell [5] mentions an unproven result by Liouville and incomplete results by Torelli and Stieltjes (see Dickson [2] , pp. 294, 295, and Dickson [6] , pp. 133, 216).
Using 13 identities about theta functions, including some important ones by Kronecker and Hermite, Bell [5] determines 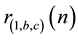 for the 10 possible ternary quadratic forms with
for the 10 possible ternary quadratic forms with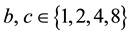 ,
,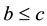 . For these forms, the corresponding counting functions depend only upon
. For these forms, the corresponding counting functions depend only upon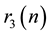 . Bell’s theorem is relevant for an important con- temporary problem, namely the theorem of Tunnel [7] , which states, conditionally on the weak Birch-Swinnterton- Dyer (BSD) conjecture for elliptic curves, a necessary and sufficient condition for a number to be congruent.
. Bell’s theorem is relevant for an important con- temporary problem, namely the theorem of Tunnel [7] , which states, conditionally on the weak Birch-Swinnterton- Dyer (BSD) conjecture for elliptic curves, a necessary and sufficient condition for a number to be congruent.
The ancient but still unsolved congruent number problem has already been studied by Diophantus, the Arab scholars of the tenth century and Leonardo of Pisa (Fibonacci) (e.g. Dickson [2] , Chap. XVI, Mordell [8] , p. 71). A positive rational number is a congruent number if it is the area of some right triangle with rational sides. As shown by Koblitz [9] , Section 1.1, one can restrict the analysis to square-free natural numbers, which will be assumed throughout. It is also known that n is a congruent number if, and only if, the elliptic curve 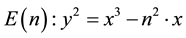 has a non-trivial rational point (for a precise constructive characterization see Hürlimann [10] , criterion (E3)). Up to the weak Birch-Swinnerton-Dyer (BSD) conjecture for the elliptic curve
has a non-trivial rational point (for a precise constructive characterization see Hürlimann [10] , criterion (E3)). Up to the weak Birch-Swinnerton-Dyer (BSD) conjecture for the elliptic curve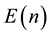 , an elegant characterization of congruent numbers has been obtained by Tunnel [7] (see Koblitz [9] , Theorem, p. 221, or Cohen [11] , Theorem 6.12.4). Nowadays, it is even possible to compute large tables of congruent numbers conditionally on the validity of the weak BSD conjecture (e.g. Cohen [11] , Remark, p. 568) without using Tunnel’s theorem. Nevertheless, this exercise requires advanced mathematics and, for this reason, Tunnel’s theorem remains attractive from the viewpoint of elementary number theory. According to this result, if
, an elegant characterization of congruent numbers has been obtained by Tunnel [7] (see Koblitz [9] , Theorem, p. 221, or Cohen [11] , Theorem 6.12.4). Nowadays, it is even possible to compute large tables of congruent numbers conditionally on the validity of the weak BSD conjecture (e.g. Cohen [11] , Remark, p. 568) without using Tunnel’s theorem. Nevertheless, this exercise requires advanced mathematics and, for this reason, Tunnel’s theorem remains attractive from the viewpoint of elementary number theory. According to this result, if ![]() is a square-free and odd, respectively even, congruent number, then one has
is a square-free and odd, respectively even, congruent number, then one has
![]() . (1.1)
. (1.1)
Moreover, if a weak form of the BSD conjecture holds (i.e. if the L-function of ![]() vanishes at 1, then the rank of
vanishes at 1, then the rank of ![]() is positive), then the converse also holds. Therefore, any computer algorithm able to verify the validity of (1.1) will produce congruent numbers under the truth of the weak BSD conjecture. Actually, Bell did a first step to make (1.1) effective by finding expressions for
is positive), then the converse also holds. Therefore, any computer algorithm able to verify the validity of (1.1) will produce congruent numbers under the truth of the weak BSD conjecture. Actually, Bell did a first step to make (1.1) effective by finding expressions for ![]() and
and ![]() that only depend upon
that only depend upon![]() . In the Sections 2 and 3, we improve Bell’s approach and display explicit finite and computable expressions for (1.1).
. In the Sections 2 and 3, we improve Bell’s approach and display explicit finite and computable expressions for (1.1).
A brief description of the content follows. In Section 2, a modern elementary proof of Bell’s theorem is given. It uses only three standard theta function identities and a set of five three-square identities by Hurwitz [12] that have been revisited in Cooper and Hirschhorn [13] . Henceforth, the proof is more direct and less complex than the original derivation by Bell [5] . In Section 3, explicit expressions for the counting functions involved in (1.1) are determined and applied to the congruent number problem. In particular, an unconditional proof that ![]() is not congruent is given. Section 4 concludes with a brief description of some old and new facts about congruent numbers.
is not congruent is given. Section 4 concludes with a brief description of some old and new facts about congruent numbers.
2. Ramanujan’s Theta Functions and Bell’s Theorem
We give a new elementary proof of Bell’s theorem. It uses Ramanujan’s theta functions
![]() , (2.1)
, (2.1)
the three basic identities
![]() , (2.2)
, (2.2)
![]() , (2.3)
, (2.3)
![]() , (2.4)
, (2.4)
and the following three squares identities of Hurwitz [12] (see Cooper and Hirschhorn [13] , Theorem 1, identities (1.3)-(1.4), (1.6)-(1.8))
![]() , (2.5)
, (2.5)
![]() , (2.6)
, (2.6)
![]() , (2.7)
, (2.7)
![]() , (2.8)
, (2.8)
![]() . (2.9)
. (2.9)
Note that (2.2)-(2.4) follow from Berndt [14] , Entry 25, p. 40. Equation (2.2) is entry 25(iv), Equation (2.3) is obtained by adding 25(i) and 25(ii), and Equation (2.4) is obtained by adding 25(v) and 25(vi).
Theorem 2.1. (Theorem of Bell). The nine counting functions![]() ,
, ![]() ,
, ![]() ,
, ![]() , are determined as follows:
, are determined as follows:
Form (1,1,2)
![]() . (2.10)
. (2.10)
Form (1,1,4)
![]() . (2.11)
. (2.11)
Form (1,1,8)
![]() (2.12)
(2.12)
Form (1,2,2)
![]() (2.13)
(2.13)
Form (1,2,4)
![]() (2.14)
(2.14)
Form (1,2,8)
![]() (2.15)
(2.15)
Form (1,4,4)
![]() . (2.16)
. (2.16)
Form (1,4,8)
![]() (2.17)
(2.17)
Form (1,8,8)
![]() (2.18)
(2.18)
Proof. Recall that the generating function of ![]() (with
(with![]() ) is determined by
) is determined by
![]() . Frequent use of (2.2)-(2.9) is made without further mention. For sim-
. Frequent use of (2.2)-(2.9) is made without further mention. For sim-
plicity the abbreviation ![]() is used. Summation always includes all natural numbers
is used. Summation always includes all natural numbers![]() .
.
Form (1,1,2). With ![]() one sees that (2.10) follows from
one sees that (2.10) follows from
![]() ,.
,.
Form (1,1,4). One has
![]()
and (2.11) is shown through the uniquely defined identifications
![]()
Form (1,1,8). A calculation shows that
![]()
which implies (2.12) through the identifications
![]()
Form (1,2,2). Similarly to the above one obtains
![]()
from which one gets (2.13) as follows:
![]()
Form (1,2,4). With successive calculation one obtains
![]()
and (2.14) follows from the identifications
![]()
Form (1,2,8). In the same manner, one gets
![]()
which implies (2.15) as follows:
![]()
Form (1,4,4). One has![]() , and one obtains (2.16) from the identities
, and one obtains (2.16) from the identities
![]()
Form (1,4,8). Through calculation one gets
![]()
and (2.17) follows from
![]()
Form (1,8,8). A successive calculation shows that
![]()
from which one gets (2.18) through identification of
![]()
The proof of Theorem 2.1 is complete. ◊
3. Tunnel’s Congruent Number Criterion
As seen in Section 1, Tunnel’s theorem depends upon the determination of the counting functions in Equation (1.1). While ![]() and
and ![]() have been determined in Section 2, it remains to find expressions for
have been determined in Section 2, it remains to find expressions for ![]() and
and ![]() that enables the computation of (1.1). We begin with the simpler case.
that enables the computation of (1.1). We begin with the simpler case.
3.1. Even Square-Free Congruent Numbers
The following auxiliary result in the style of Bell is required.
Lemma 3.1. Let![]() , respectively
, respectively![]() , be the coefficient of
, be the coefficient of ![]() in the
in the ![]() -expansion of
-expansion of![]() ,
,
respectively![]() . Then, the counting function
. Then, the counting function ![]() is determined as follows:
is determined as follows:
![]() (3.1)
(3.1)
Proof. We proceed similarly to the proof of Theorem 2.1. One has
![]()
from which one obtains (3.1) through the uniquely defined identifications
![]() ◊
◊
We are ready for the following result.
Theorem 3.1. (Even square-free congruent numbers) Suppose the weak BSD conjecture holds and let n = 2m be a square-free number. Two cases can occur.
Case 1: If![]() , then
, then ![]() is congruent.
is congruent.
Case 2: ![]()
The number ![]() is congruent if, and only if, one has
is congruent if, and only if, one has![]() , where this equation is determined by the formulas
, where this equation is determined by the formulas
![]() . (3.2)
. (3.2)
Proof. Case 1 is easy. If m = 4j + 3 then by (2.17) and (3.1) one has ![]() and the result follows by (1.1) and the weak BSD conjecture. Consider now Case 2 and suppose that
and the result follows by (1.1) and the weak BSD conjecture. Consider now Case 2 and suppose that![]() . Using (2.17) and (2.8) one sees that
. Using (2.17) and (2.8) one sees that
![]() ,
,
where ![]() is the number of representations of
is the number of representations of ![]() as a sum of two triangular numbers. The right-hand side is a convolution sum with coefficients
as a sum of two triangular numbers. The right-hand side is a convolution sum with coefficients
![]() .
.
Using that ![]() and rearranging one obtains the first formula in (3.2). The used identity between squares and triangles is part of more general similar relationships due to Bateman and Knopp [15] (see also Barrucand, Cooper and Hirschhorn [16] and Cooper and Hirschhorn [17] ). For the second formula one proceeds similarly. With Lemma 3.1 one has
and rearranging one obtains the first formula in (3.2). The used identity between squares and triangles is part of more general similar relationships due to Bateman and Knopp [15] (see also Barrucand, Cooper and Hirschhorn [16] and Cooper and Hirschhorn [17] ). For the second formula one proceeds similarly. With Lemma 3.1 one has
![]() , which implies
, which implies
![]() and the second formula in (3.2). ◊
and the second formula in (3.2). ◊
Remark 3.1. The first formula in (3.2) implies some identities between squares (respectively triangles) and certain partial sums of Jacobi symbols. Indeed, alternatively to the above one has with Cooper and Hirschhorn [3] , Theorem 3, Equation (1.28), the formulas
![]()
3.2. Odd Square-Free Congruent Numbers
Again, one needs an auxiliary result.
Lemma 3.2. Let![]() , respectively
, respectively![]() , be the coefficient of
, be the coefficient of ![]() in the
in the ![]() -expansion of
-expansion of
![]() , respectively
, respectively![]() . Then, the counting function
. Then, the counting function
![]() for odd m is determined as follows:
for odd m is determined as follows:
![]() . (3.3)
. (3.3)
Proof. As in the proof of Theorem 2.1 one has
![]()
The first product with ![]() replaced by
replaced by ![]() is the generating function of the Bell form (1,2,8) in Theorem 2.1 and contributes to the counting function for numbers divisible by 4. Similarly, the second product contributes to the counting function for numbers divisible by 2. The only contributions to
is the generating function of the Bell form (1,2,8) in Theorem 2.1 and contributes to the counting function for numbers divisible by 4. Similarly, the second product contributes to the counting function for numbers divisible by 2. The only contributions to ![]() for odd m stem from the third and fourth product. For these one has
for odd m stem from the third and fourth product. For these one has
![]()
Since there is no contribution to the counting function for odd numbers congruent to 5 and 7 mod 8, the Lemma is shown. ◊
Theorem 3.2. (Odd square-free congruent numbers). Suppose the weak BSD conjecture holds and let m be an odd square-free number. Three cases can occur.
Case 1: If![]() , then m is not congruent (independently of the weak BSD conjecture).
, then m is not congruent (independently of the weak BSD conjecture).
Case 2: If![]() , then m is congruent.
, then m is congruent.
Case 3: ![]()
The number ![]() is congruent if, and only if, one has
is congruent if, and only if, one has![]() , where this equation is determined by the formulas
, where this equation is determined by the formulas
![]() (3.4)
(3.4)
Proof. We begin with Case 2. If ![]() then by (2.15) and (3.3) one has
then by (2.15) and (3.3) one has
![]() and the result follows by (1.1) and the weak BSD conjecture. Consider now Case 3 and suppose that
and the result follows by (1.1) and the weak BSD conjecture. Consider now Case 3 and suppose that![]() . Using (2.15) and (2.7) one sees that
. Using (2.15) and (2.7) one sees that
![]() ,
,
which implies the first formula in (3.4). According to Lemma 3.2 one can write
![]() , where
, where ![]() and
and ![]() are the coefficients of
are the coefficients of ![]() in the
in the ![]() -expansions of
-expansions of ![]() and
and ![]() respectively. Therefore, one has
respectively. Therefore, one has
![]() ,
,
which yields the first sum in the second formula of (3.4). Similarly, one has
![]() .
.
Making use of the fact that ![]() (see the proof of Theorem 3.1) one obtains the second sum in (3.4). It remains to show Case 1. Using (2.15) one has
(see the proof of Theorem 3.1) one obtains the second sum in (3.4). It remains to show Case 1. Using (2.15) one has
![]() .
.
On the other hand from Lemma 3.2 one knows that
![]() .
.
Clearly, the theta function product ![]() is the generating function for the number
is the generating function for the number ![]() of representations of
of representations of ![]() in the form
in the form
![]() ,
,
where![]() ,
, ![]() with
with![]() , are triangular numbers. Now, one has the following
, are triangular numbers. Now, one has the following
one-to-one correspondence between solutions of ![]() and
and![]() . If
. If
![]() , then without loss of generality
, then without loss of generality ![]() and
and![]() . Through permutations one can arrange that
. Through permutations one can arrange that ![]() and
and![]() . One sees that
. One sees that
![]() ,
,
are non-negative integers that satisfy the equations
![]() ,
,
hence![]() . Taking into account permutations and sign changes one must have
. Taking into account permutations and sign changes one must have
![]() . Through application of Tunnel’s theorem one sees that
. Through application of Tunnel’s theorem one sees that
![]() ,
,
which is strictly positive by the Gauss-Legendre theorem on the sum of three squares. Case 1 follows and the proof is complete. ◊
Remark 3.2. Similarly to Remark 3.1, the first formula in (3.4) implies the following identity (see Cooper and Hirschhorn [3] , Theorem 3, Equation (1.28))
![]() .
.
4. Notes on Congruent Numbers