Bulk Viscous Anisotropic Cosmological Models with Dynamical Cosmological Parameters G and ∧ ()
1. Introduction
It is well known that majority of exact solutions of Einstein’s field equations representing cosmological models of relativity for spatially homogeneous space times belongs to either Bianchi types or Kantowaski-Sachs models [1] . The isotropic Friedman-Robertson-Walker (FRW) models are special cases of anisotropic Bianchi type models. The present day cosmological observations provide strong evidence for homogeneous, isotropic and accelerating expansion of the universe. However, in its early stages of evolution, universe might have not so smoothed behavior. Experimental data and number of scientific arguments in the literature support the existence of anisotropic stage of universe which is supposed to be phased out during evolution of the universe. In order to study the early stages behavior of evolution of universe, several authors have studied different Bianchi types and Kantowski-Sachs cosmological models. Bianchi type I space-time become almost first choice of researchers for study of anisotropic expansion of the universe as it is the simplest generalization of the flat FRW space-time. A number of authors have studied various anisotropic cosmological models in different context [2] -[15] . Recently Pradhan et al. [16] have studied a new class of cosmological models in scalar tensor theory of gravitation. Bianchi type I cosmological models with viscous fluid in modified Brans-Dicke cosmology have been studied by Rai et al. [17] .
The cosmological “constant” L which was originally introduced by Einstein in 1917 in his field equations has fallen in and out of researchers interest several times. Its significance has been studied from time to time by various researchers. It is believed that the cosmological constant was very large in the early universe, relaxed to its present small value in the course of expansion of the universe by creating massive or mass less particles. Padmanabhan [18] pointed out that the observations, suggesting the existences of non zero cosmological constant, raise serious theoretical problems. The large discrepancy between the observational value of L and the theoretical value is termed as cosmological constant problem.
Many solutions convening to this problem were proposed by considering dynamical L [19] -[26] . It is predicted that the presence of a non zero cosmological constant is one of the most important reason for the acceleration [27] [28] . Discussion on cosmological constant problems and consequences on cosmology with a time varying cosmological constant is presented by several authors [29] [30] .
The Newtonian constant of gravitation G, plays a roll of coupling constant between geometry and matter in Einstein field equation. In order to achieve possible unification of gravitation and elementary particle physics or to incorporate Mach’s principle in general relativity, many other extension of Einstein theory with time dependent G have been proposed. A number of authors [31] -[40] have studied the variation of G and L , within the frame work of general relativity in different context.
It has been suggested in the literature that bulk viscosity is associated with grand unified theory, phase transition and string creation. Further bulk viscosity acts like a negative energy field in an expanding universe. Maartens [41] has presented exhaustive review of cosmological models with causal thermodynamics. Singh and Kale [42] have studied bulk viscous Bianchi Type V cosmological models with varying gravitational and cosmological constant. Recently Verma and Shriram [43] [44] have investigated Bianchi Types bulk viscous cosmological models with variable G and L . Singh [45] has discussed some cosmological models with time varying gravitational cosmological constants. Pradhan et al. [46] have investigated Bianchi type I transit cosmological models with time dependent gravitational and cosmological constants.
2. Field Equations
In this paper we have considered that the gravitational field of matter distribution is represented by a Bianchi type I metric space time.
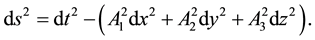 (1)
(1)
Einstein field equations with cosmological “constant” for perfect fluid distribution are given by
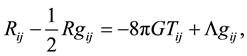 (2)
(2)
where, the energy momentum tensor is given by
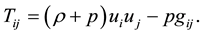
It is well known that in order to consider the effect of bulk viscosity, energy momentum tensor 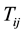 may be considered as
may be considered as
 (3)
(3)
Here,  is the energy density, p represent perfect fluid pressure and
is the energy density, p represent perfect fluid pressure and 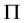 stands for bulk viscous stress.
stands for bulk viscous stress.
The Einstein’s field Equation (2) for the space-time metric (1) yields following equations
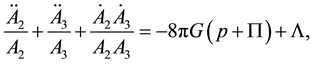 (4)
(4)
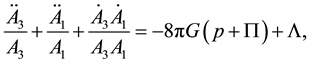 (5)
(5)
 (6)
(6)
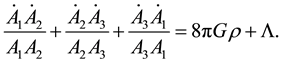 (7)
(7)
By a combination of Equations (4)-(7), one can easily obtain
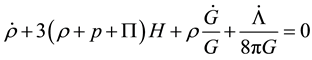 (8)
(8)
where 
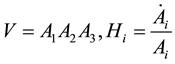
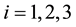 .
.
The energy momentum conservation equation 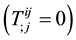 suggests
suggests
![]() (9)
(9)
From Equations (8) and (9) we have
![]() (10)
(10)
Further, Equations (4)-(6) yield the solutions
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
Here ![]() and
and ![]() are integration constants obeying the relation
are integration constants obeying the relation
![]()
The above results suggest that the metric function can be explicitly expresses in terms of volume V of the universe represented by Bianchi type I space-time. Now assuming a power law relation between the volume of the universe and it’s age
![]() (14)
(14)
Equations (11)-(13) take the form
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
When n = 1, from Equations (11)-(13) and using (14), we have
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
With help of Equations (15)-(17), Hubble parameter H and deceleration parameter q can be obtained as
![]() (21)
(21)
It can be easily seen that for accelerating model of the universe n > 3.
The shear scalar ![]() may be defined as [47]
may be defined as [47]
![]()
which in this model takes the form
![]() (22)
(22)
AS ![]() shear dies out.
shear dies out.
The state finder parameter are given by
![]()
which is this model takes the form
![]() (23)
(23)
3. Cosmological Models
In this section we shall consider different cases to discuss behavior of cosmological models.
3.1. Case I
In this case we consider ansatz given by Arbab [48]
![]() (24)
(24)
Using Equations (15)-(17) and (24), Equation (7) takes the form
![]() (25)
(25)
where ![]()
From Equations (10) and (24), we have
![]() (26)
(26)
On dividing Equation (26) by Equation (25) and then integrating, one can obtain
![]() (27)
(27)
From Figure 1 one can see that cosmological constant is increasing with evolution of the universe.
Using observational values ![]() we have
we have![]() . Here we consider n = 5.
. Here we consider n = 5.
By use of Equations (25) and (27), we can get the relation between energy density and cosmic time as
![]() (28)
(28)
The condition ![]() ensures the positivity of energy density. It can be easily seen that the energy density is always decreasing during evolution of the universe for
ensures the positivity of energy density. It can be easily seen that the energy density is always decreasing during evolution of the universe for ![]() .
.
From Figure 2 one can see that energy density is decreasing with evolution of the universe.
Using observational values ![]() we have
we have ![]()
Considering equation of state ![]() and Equation (24), the Equation (6) may be written as
and Equation (24), the Equation (6) may be written as
![]() , (29)
, (29)
With the help of Equations (15) and (16), Equation (29) suggests
![]() (30)
(30)
From Equations (25) and (30), we get
![]() (31)
(31)
Equation (31) shows that bulk viscous pressure ![]() decreases with evolution of the universe.
decreases with evolution of the universe.
The critical energy density and the critical vacuum energy density are respectively given by
![]()
For the anisotropic model can be expressed respectively as
![]() (32)
(32)
![]() (33)
(33)
Mass density parameter and the density parameter of the vacuum are given by
![]()
For the anisotropic Bianchi type I model can be expressed respectively as
![]() (34)
(34)
![]() (35)
(35)
3.2. Case II
Several authors have considered the Chen and Wu [49] ansatzs![]() . Motivated by their consideration in this case we have assumed
. Motivated by their consideration in this case we have assumed
![]()
Figure 1. Shows variation of G with cosmic time t. Here we consider n = 5 and![]() .
.
![]()
Figure 2. Shows the variation of ρ with respect to cosmic time t. Here we consider![]() .
.
![]() (36)
(36)
Now with the help of Equations (15)-(17) and (36), Equation (7) takes the form
![]() (37)
(37)
Differentiating Equation (36) and using Equation (10), we get
![]() (38)
(38)
From Equations (37) and (38), one can easily obtain the solution for G in terms of cosmic time t.
![]() (39)
(39)
where ![]() is the constant of integration.
is the constant of integration.
By using Equations (37) and (39), we have
![]() (40)
(40)
Here ![]() , ensures the positivity of energy density. It can be easily seen that
, ensures the positivity of energy density. It can be easily seen that ![]() is decreasing for all values of n > 1.
is decreasing for all values of n > 1.
Figure 3 shows behavior of energy density against cosmic time t. One can see that energy density is decreasing with evolution of the universe.
With help of Equations (15)-(16) and (36), Equation (6) reduces to
![]() (41)
(41)
Further, from Equations (37) and (41), we get
![]() (42)
(42)
The critical energy density and the critical vacuum energy density for this model can be expressed as
![]() (43)
(43)
![]() (44)
(44)
Mass density parameter and the density parameter of the vacuum for this model are given by
![]() (45)
(45)
![]() (46)
(46)
3.3. Case III
Chen and Wu ansatz [49] was generalized by Carvalho et al. [50] by considering ![]() . On the similar line in this case we have modified assumption of case II by adding the term
. On the similar line in this case we have modified assumption of case II by adding the term ![]()
![]() (47)
(47)
Now, under the assumption (47), Equation (7) may be written as
![]() (48)
(48)
Differentiating Equation (47) and using Equation (10), we get
![]() (49)
(49)
From Equations (48) and (49) one can easily write expression for G in terms of t as
![]() (50)
(50)
From Figure 4 one can see that cosmological constant is increasing with evolution of the universe.
Again, with help of Equation (50), Equation (48) gives energy density
![]() (51)
(51)
![]()
Figure 3. Shows behavior of energy density against cosmic time t.
![]()
Figure 4. Shows variation of G with cosmic time t. Here we consider n = 5 and ![]()
where
![]()
The condition ![]() and
and ![]() ensure the positivity of
ensure the positivity of ![]() . Further one can easily see that
. Further one can easily see that ![]() is decreasing with the evolution of universe.
is decreasing with the evolution of universe.
From Figure 5 one can see that energy density is decreasing with evolution of the universe.
On the similar line of previous sections, we have obtained the expression for bulk viscous stress as
![]() (52)
(52)
The critical energy density and the critical vacuum energy density for this model can be expressed as
![]() (53)
(53)
![]()
Figure 5. Shows behavior of energy density against cosmic time t. Here we consider n = 5 and ![]()
![]() (54)
(54)
Mass density parameter and the density parameter of the vacuum for this model are given by
![]() (55)
(55)
![]() (56)
(56)
4. Discussion
Presently it is well accepted fact that the expansion of the universe is accelerating at present epoch. For an accelerating model of the universe deceleration parameter must be negative (q < 0) and hence Equation (21) suggests n > 3. Considering the value n > 3 Equations (15)-(17) indicate that anisotropy will phase out with evolution of the universe and model approaches to isotropic cosmological model. For n = 1, q > 0 model has decelerated expansion. In case II, if we take n = 1 the cosmological constant ![]() similar to the results obtained Beesham [51] . This relation of
similar to the results obtained Beesham [51] . This relation of ![]() and cosmic time t has been discussed by several authors [52] [53] . Further the model suggests the relation
and cosmic time t has been discussed by several authors [52] [53] . Further the model suggests the relation ![]() . This type of result has been reported in the references ([52] [53] and references their in). When the cosmic time t approaches infinity expansion stops and shear dies out. In order to have clear idea of variation in behavior of cosmological parameters several relevant graphs have been plotted. All graphs of cosmological parameters are in fair agreement with cosmological observations.
. This type of result has been reported in the references ([52] [53] and references their in). When the cosmic time t approaches infinity expansion stops and shear dies out. In order to have clear idea of variation in behavior of cosmological parameters several relevant graphs have been plotted. All graphs of cosmological parameters are in fair agreement with cosmological observations.
Acknowledgements
Authors would like to thank U.G.C. New Delhi for providing financial support under the scheme of Major research project (F. No. 41-765/2012(SR)).