Least-Squares Finite Element Method for the Steady Upper-Convected Maxwell Fluid ()
1. Introduction
In recent years, there has been an increased interest in the least-squares finite element method for the approximation of partial differential equations, see e.g. [1] -[6] . This technique is attractive because the linear systems generated by the discretization are symmetric and positive definite, thus the algebraic system can be solved by fast direct or iterative algorithms. Moreover, in contrast to the mixed finite element method, the inf-sup or LBB type of conditions is naturally satisfied. However, without the weights in the least-squares functional, this method results in poor numerical solutions even for simple problems. In [7] , Bochev and Gunzburger pointed that the weighted least-squares method was optimal for the velocity-pressure-stress formulation of the Stokes equations. The weighted least-squares method has also been used to solve other viscoelastic problems, such as the Oldroyd-B, Carreau, and Phan-Thien-Tanner models [1] [3] [8] .
In the viscoelastic fluids of the differential type, the constitutive equations consist of an algebraic tensorial relationship between the stress tensor and the rate of deformation tensor. The upper-convected Maxwell fluid [9] is the simplest, if not the easiest, representative of that class and has served as a model fluid for developing numerical techniques. The purpose of this paper is to present a finite element method for the upper-convected Maxwell fluid which is one of the most used viscoelastic models. The nonlinear model is first approached by linearizing the equations and a weighted least-squares finite element method is applied to solve the linear equations. Error estimates of the finite element solutions to the linear system are derived.
2. Governing Equations
Assume that 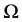 is a bounded and connected domain in
is a bounded and connected domain in  with Lipschitz boundary
with Lipschitz boundary . We consider the steady incompressible flows governed by the conservation equations for mass and momentum
. We consider the steady incompressible flows governed by the conservation equations for mass and momentum
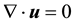 (2.1)
(2.1)
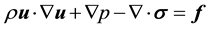 (2.2)
(2.2)
where 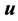 denotes the velocity vector,
denotes the velocity vector, 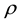 the constant density,
the constant density, 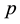 the pressure,
the pressure,  the extra-stress tensor and
the extra-stress tensor and 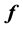 the body force.
the body force.
For the upper-convected Maxwell model, the extra-stress tensor 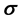 satisfies the following constitutive equation
satisfies the following constitutive equation
 (2.3)
(2.3)
where 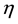 is the constant viscosity,
is the constant viscosity, 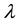 the relaxation time and
the relaxation time and  the standard strain rate tensor. The subscript (1) denotes the upper-convected material derivative
the standard strain rate tensor. The subscript (1) denotes the upper-convected material derivative

and
![]()
To simplify our analysis, homogeneous boundary conditions are assumed on![]() . The results in this article can be extended to nonhomogeneous boundary conditions easily. Collecting (2.1)-(2.3), we obtain the steady UCM model
. The results in this article can be extended to nonhomogeneous boundary conditions easily. Collecting (2.1)-(2.3), we obtain the steady UCM model
![]() (2.4)
(2.4)
3. Mathematical Notation and Preliminaries
Throughout the paper, we use the standard notation and definition for the Sobolev spaces![]() ,
, ![]() , with inner products and norms denoted by
, with inner products and norms denoted by ![]() and
and![]() . For
. For![]() , we write
, we write![]() ,
, ![]() and
and![]() . As usual,
. As usual, ![]() denotes the closure of
denotes the closure of ![]() with respect to the norm
with respect to the norm ![]() and
and ![]() denotes the space of squ- are integrable functions with zero mean
denotes the space of squ- are integrable functions with zero mean
![]() .
.
The spaces ![]() with positive values of
with positive values of ![]() is defined as the dual space of
is defined as the dual space of ![]() with the following norm
with the following norm
![]() (3.1)
(3.1)
where ![]() stands for the duality pairing between
stands for the duality pairing between ![]() and
and![]() .
.
We use the following approximation
![]()
to linearize the equations in (2.4). Moreover we assume that ![]() and the approximation satisfies
and the approximation satisfies
![]() . (3.2)
. (3.2)
We introduce the replacement rules
![]()
![]()
![]()
which result in the linearized system
![]() (3.3)
(3.3)
where
![]()
![]()
![]()
The velocity![]() , the pressure
, the pressure ![]() and the extra-stress tensor
and the extra-stress tensor ![]() belong to their respective spaces
belong to their respective spaces
![]()
![]()
![]()
and let![]() .
.
Based on [7] , we define the weighted least-squares functional for the linearized system (3.3)
![]() (3.4)
(3.4)
Now we show that the homogeneous least-squares functional of (3.4) is equivalent to the norm
![]() .
.
Theorem 1. There exist positive constants ![]() and
and![]() , which depend on
, which depend on![]() ,
, ![]() and
and![]() , such that
, such that
![]() (3.5)
(3.5)
hold for any![]() .
.
Proof. The upper bound in (3.5) follows easily from the triangle inequality and (3.2). For the lower bound, we will show that
![]() (3.6)
(3.6)
where
![]() .
.
Using the Green’s formula and Cauchy-Schwarz inequality, we obtain
![]()
for any![]() . By using Lemma 2.1 in [10] as
. By using Lemma 2.1 in [10] as
![]()
we obtain
![]()
which implies that
![]() . (3.7)
. (3.7)
Similarly, we have
![]() (3.8)
(3.8)
By the arguments similar to Theorem 4.1 in [11] , we obtain
![]() (3.9)
(3.9)
Combining (3.7)-(3.9) yields (3.6).
From the inequality![]() , we establish
, we establish
![]() (3.10)
(3.10)
Note that
![]()
and, using (3.10),
![]()
where ![]() for
for ![]() and
and ![]() chosen sufficiently small. This completes the proof.
chosen sufficiently small. This completes the proof.
However the least squares functional ![]() is not practical. The negative order Sobolev norm
is not practical. The negative order Sobolev norm
![]() leads to difficulties in the assembly of the linear algebraic equations. In [7] , Bochev and Gunzburger used the weighted norm
leads to difficulties in the assembly of the linear algebraic equations. In [7] , Bochev and Gunzburger used the weighted norm ![]() where
where ![]() denotes some parameter of the finite element space instead of the norm
denotes some parameter of the finite element space instead of the norm![]() . Hence we will consider the mesh dependent functional in which the residuals of each equation in
. Hence we will consider the mesh dependent functional in which the residuals of each equation in ![]() -norm are multiplied by proper mesh dependent weights.
-norm are multiplied by proper mesh dependent weights.
4. Finite Element Approximations
We assume that the domain ![]() is a polygon, and
is a polygon, and ![]() is a triangulation of
is a triangulation of ![]() made of triangular elements
made of triangular elements ![]() with
with![]() . Thus, the computational domain is given by
. Thus, the computational domain is given by
![]() .
.
We assume that the partition ![]() is regular and satisfies the inverse assumption. Let
is regular and satisfies the inverse assumption. Let ![]() denote the space of polynomials on
denote the space of polynomials on ![]() of degree less or equal to
of degree less or equal to![]() . We define the finite element spaces for the approximation of
. We define the finite element spaces for the approximation of ![]() as follows
as follows
![]()
![]()
![]() .
.
Let ![]() be a finite dimensional subspace of X with the following approximation properties:
be a finite dimensional subspace of X with the following approximation properties:
![]() (3.11)
(3.11)
where ![]() and
and![]() . The space
. The space ![]() admits the property
admits the property
![]() (3.12)
(3.12)
with ![]() and
and![]() . The properties hold for finite element spaces consisting of continuous piecewise polynomials based on quasi-uniform triangulations [11] [12] .
. The properties hold for finite element spaces consisting of continuous piecewise polynomials based on quasi-uniform triangulations [11] [12] .
The mesh dependent least squares functional is defined by the weighted sum in ![]() -norms of the residuals of the equations in (3.3)
-norms of the residuals of the equations in (3.3)
![]() (3.13)
(3.13)
where ![]() is a positive constant. The least squares finite element problem is to minimize this functional over Xh: seek
is a positive constant. The least squares finite element problem is to minimize this functional over Xh: seek ![]() such that
such that
![]() .
.
The minimizer of (3.13) necessarily satisfies the Euler-Lagrange equation given by
![]() (3.14)
(3.14)
where
![]()
![]()
and the double-dot product is defined as
![]()
Based on Theorem 1, we establish the ellipticity of the functional ![]() in Theorem 2.
in Theorem 2.
Theorem 2. For any![]() , there exist positive constants
, there exist positive constants ![]() and
and![]() , which depend on
, which depend on![]() ,
, ![]() and
and![]() , such that
, such that
![]() , (3.15)
, (3.15)
for![]() .
.
Proof. The first inequality in (3.15) is straightforward from Theorem 1. To prove the upper bound, we assume that the spaces ![]() and
and ![]() satisfy the following inverse inequalities
satisfy the following inverse inequalities
![]()
and
![]() .
.
From the triangle inequality, we obtain
![]()
This completes the proof of the theorem.
By virtue of Theorem 2 and the Lax-Milgram theorem, we establish the following theorem.
Theorem 3. For any![]() , the functional (3.13) has the unique minimizer out of
, the functional (3.13) has the unique minimizer out of![]() , i.e., there exists a unique solution satisfies the Euler-Lagrange equation (3.14).
, i.e., there exists a unique solution satisfies the Euler-Lagrange equation (3.14).
Now we derive error estimates for the least-squares finite element solution ![]() which satisfies (3.14).
which satisfies (3.14).
Theorem 4. Assume that ![]() is the solution to (3.3), then the least-squares finite element solution
is the solution to (3.3), then the least-squares finite element solution ![]() satisfies
satisfies
![]() , (3.16)
, (3.16)
for![]() .
.
Proof. From Theorem 2, we obtain the following bound
![]() .
.
Combining the properties (3.11) and (3.12), we have
![]()
This completes the proof of the theorem.
5. Conclusion
In this paper, we have proposed and analyzed a weighted least-squares method for the approximate solution of the upper-convected Maxwell fluid. The weights in our least-squares functional involve mesh dependent weight and mass conservation constant. The homogenous functional is shown to be equivalent to a natural norm. A prior error estimate is given for the finite element solutions. An adaptive least-squares finite element method for this viscoelastic fluid model will be discussed in the future.
Acknowledgements
The authors’ work is supported by the National Science Foundation of China (No. 11271247) and the Natural Science Foundation of Hebei Province (No. G2013402063).