1. Preliminaries
One of the main objective of algebraic coding theory is to classify codes up to equivalence by using a list of invariants. The present work is following this way. We study here a class of linear binary codes whose all codewords have distinct weight and will give a classification theorems. Throughout this work all codes are
linear binary codes. We call an 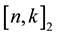 -binary code every
-binary code every 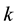 dimensional subspace
dimensional subspace 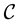 of
of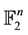 . Recall also that
. Recall also that
the Hamming weight  of vector
of vector  is defined to be the number of nonzero components of
is defined to be the number of nonzero components of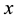 . The mi- nimum of weights where
. The mi- nimum of weights where 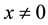 is the minimal distance
is the minimal distance 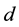 of the code.
of the code.
A Hamming isometry of 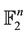 is a linear application
is a linear application 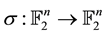 such that
such that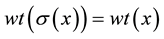 , for every
, for every
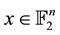 . It is well known that in binary case, the isometries are merely the permutations of the coordinates, that is the elements of
. It is well known that in binary case, the isometries are merely the permutations of the coordinates, that is the elements of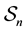 , the permutation group of
, the permutation group of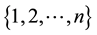 .
.
Two codes ![]() and
and ![]() are said to be equivalent if there exists an isometry
are said to be equivalent if there exists an isometry ![]() of
of ![]() such that
such that![]() . An automorphism of
. An automorphism of ![]() is a Hamming isometry
is a Hamming isometry ![]() such that
such that![]() . The automorphisms of
. The automorphisms of ![]() form a subgroup of
form a subgroup of ![]() called the automorphism group of
called the automorphism group of ![]() and we denote it by
and we denote it by![]() . Note also that the vector
. Note also that the vector
space ![]() can be endowed with a product
can be endowed with a product![]() , so that
, so that ![]() becomes
becomes
a Boolean ring. Furthermore, ![]() , for every
, for every![]() . The code
. The code ![]() is said
is said
a constant-weight code (CW-code) if all nonzero codewords have the same weight. The dual of binary
Hamming codes ![]() are simplex codes
are simplex codes ![]() of parameters
of parameters![]() . simplex codes
. simplex codes ![]() are constant
are constant
weight code (CW-code).
Any permutation of the columns of a k by n binary matrix ![]() which maps the rows of
which maps the rows of ![]() into rows of the same matrix, is called an automorphism of the binary matrix
into rows of the same matrix, is called an automorphism of the binary matrix ![]() [1] . The set of all automorphisms of
[1] . The set of all automorphisms of ![]() is a subgroup of the symmetric group
is a subgroup of the symmetric group ![]() and we denote it by
and we denote it by![]() . More treatment of linear codes can be found in the book [2] .
. More treatment of linear codes can be found in the book [2] .
Ideally, we would like the rate ![]() to be high, in order to be able to send a large number of errors. The
to be high, in order to be able to send a large number of errors. The
rate of a DW-code approch zero very quickly when the code length increase: ![]() as shown
as shown
in Figure 1 where ![]() and
and![]() , so
, so![]() .
.
It is more convenient to use the DW-codes in the construction of other codes by using some technic of construction and not to use it alone.
2. Distinct weight codes
Definition 1 A linear binary code ![]() of length
of length ![]() is said to be a Distinct Weight Code, (in short: DW-code), if
is said to be a Distinct Weight Code, (in short: DW-code), if
the weight mapping:![]() , is one to one, that is
, is one to one, that is ![]() whenever
whenever![]() ,
,![]() .
.
The simplest example of such codes are the repetition codes. Later we shall give more nontrivial examples. Let ![]() a DW-code of length
a DW-code of length ![]() and dimension
and dimension![]() . Since the number of element of
. Since the number of element of ![]() is
is![]() , then we have
, then we have![]() . In the sequel we fix our interest to the extreme case
. In the sequel we fix our interest to the extreme case![]() , in which we give a construction.
, in which we give a construction.
Proposition 2 Let ![]() such that
such that![]() . Then every family
. Then every family ![]() of words such that
of words such that ![]() is linearly independent.
is linearly independent.
Proof. Suppose on the contrary that ![]() are not linearly independent, then we have a linear combi-
are not linearly independent, then we have a linear combi-
nation![]() , where some
, where some ![]() is nonzero. Let
is nonzero. Let ![]() be the maximal integer such that
be the maximal integer such that![]() . Then
. Then
![]() , and
, and![]() . Now taking the weights leads to:
. Now taking the weights leads to:
![]()
a contradiction. ![]()
Now we give a construction of a ![]() DW-code.
DW-code.
Let ![]() be a nonzero integer and
be a nonzero integer and![]() . Take
. Take ![]() the canonical basis of
the canonical basis of![]() . Put
. Put![]() ,
,
then clearly![]() . By the proposition 2, the code-words
. By the proposition 2, the code-words ![]() are linearly independent and
are linearly independent and
generate a ![]() linear code that we denotes by
linear code that we denotes by![]() . It also seen that
. It also seen that![]() , whenever
, whenever![]() . This
. This
implies that![]() .
.
A generator matrix of ![]() looks like:
looks like:
![]()
Proposition 3 The ![]() -code
-code ![]() is a DW-code.
is a DW-code.
Proof. Since the cardinal of ![]() is
is![]() , it suffices to show that wt:
, it suffices to show that wt: ![]() is onto.
is onto.
Let![]() , then
, then ![]() can be written
can be written ![]() in the base 2, where
in the base 2, where![]() . Set
. Set![]() ,
,
then![]() .
.![]()
Up an equivalence we have the following result:
Theorem 4 There exists only one distinct weight ![]() -code, moreover such code is Boolean subring of
-code, moreover such code is Boolean subring of
![]() .
.
Proof. Let ![]() be such a code and take code-words
be such a code and take code-words![]() , each
, each ![]() has weight
has weight![]() . These are linearly independent and form a basis of
. These are linearly independent and form a basis of![]() . Next we show that
. Next we show that![]() ,
,![]() . Otherwise, there exists a
. Otherwise, there exists a
least integer ![]() such that
such that ![]() for some
for some![]() . Since
. Since![]() , one have
, one have![]() .
.
Multiplying by ![]() yields
yields![]() . Now consider the word
. Now consider the word![]() ,
,
![]() On the other hand, if we
On the other hand, if we
consider![]() , then
, then![]() . Thus
. Thus ![]() hence
hence
![]() a contradition. This means that
a contradition. This means that![]() , if
, if![]() . Since
. Since![]() , and
, and ![]() is a
is a
basis of![]() , then
, then ![]() is a Boolean ring.
is a Boolean ring.
Now we define a linear mapping ![]() by
by![]() . Then,
. Then,![]() . If
. If
![]() , then
, then![]() . This implies that
. This implies that ![]()
is an isometry between ![]() and
and![]() , and by the extension theorem of MacWilliams, see [3] or [4] , there
, and by the extension theorem of MacWilliams, see [3] or [4] , there
exists a permutation![]() , such that
, such that![]() .
.![]()
Example 5 ![]() and
and ![]()
![]()
By using the software Q-extension, see [5] we show, up to equivallence, that among six equivallence classes
the unique DW-code ![]() of parametters
of parametters ![]() is the code of generator matrix
is the code of generator matrix![]() . It is clear
. It is clear
that it is equivallent to the code ![]() of generator matrix
of generator matrix![]() . Just swap the second and third
. Just swap the second and third
rows and then apply the permutation![]() .
.
Theorem 6 Let![]() , Diophantine equations
, Diophantine equations ![]() for which
for which
![]()
![]()
![]()
![]() ,
,![]() ,
,![]() ,
,
have a unique solution which is the k-uplet![]() .
.
Proof. ![]() is clearly a solution of the Diophantine equation which satisfies the conditions
is clearly a solution of the Diophantine equation which satisfies the conditions
(1). Assume that ![]() for some
for some ![]() and
and![]() , then
, then ![]()
![]() where
where
![]() and
and![]() . We can assume without loss of generality that
. We can assume without loss of generality that
![]() . So by the uniqueness of Development of any integer less than or equal
. So by the uniqueness of Development of any integer less than or equal ![]()
in binary basis, the equality ![]() leads to a contradiction. So the solution
leads to a contradiction. So the solution ![]()
satisfies the conditions (2).
Conversely, Let ![]() a solution of the equation
a solution of the equation ![]() satisfying (1)-(2). We can
satisfying (1)-(2). We can
take![]() ,
, ![]() elements of
elements of ![]() such that
such that ![]() and
and![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() are linearly independent. The
are linearly independent. The
condition (2) means that the code of generator matrix ![]() is a dw-code. On after Theorem 1.3, the
is a dw-code. On after Theorem 1.3, the
condition (1) implies that there exists an invertible ![]() by
by ![]() matrix
matrix ![]() and a permutation matrix
and a permutation matrix
![]() such that
such that ![]() where
where ![]() and
and ![]()
is the generator matrix of the code![]() . It is clear that
. It is clear that ![]() is of the form:
is of the form:
![]()
where ![]() or 1,
or 1, ![]() and
and ![]() we have
we have![]() . So we have
. So we have
![]() , and then we have
, and then we have![]() ,
, ![]() by the
by the
uniqueness of development of ![]() in binary basis. By (1) we have
in binary basis. By (1) we have
![]() , then we have:
, then we have:![]() ,
, ![]()
![]() Kronecker symbol
Kronecker symbol![]() .
.
Since![]() , we have
, we have![]() ,
, ![]() and finally we have
and finally we have
![]()
![]() .
.
Remark 7 Without the conditions (1) and (2), Diophantine equations have ![]() different solutions. For all
different solutions. For all
![]() note that there is no DW-self-dual code. Indeed, if not, we will have
note that there is no DW-self-dual code. Indeed, if not, we will have![]() , wich is impossible.
, wich is impossible.
3. classification and automorphism group of DW-Codes
3.1. Automorphism Group: thegeneral case
We consider, without loss of generality, that a generator matrix of a DW-code has no zero columns. Indeed, if this is the case, the zero columns are omitted and we consider the obtained DW-code. This assumption is made in the entier paper. We study the automorphism group of DW-codes. We first notice the following:
Proposition 8 Let ![]() any basis of an
any basis of an ![]() DW-code. Then
DW-code. Then
![]() .
.
Moreover, if ![]() any generator matrix of
any generator matrix of![]() , then
, then ![]() is an automorphism of
is an automorphism of![]() , if and only if,
, if and only if, ![]() is an automorphism of the binary matrix
is an automorphism of the binary matrix![]() .
.
Proof. Clear.
Proposition 9 The automorphism group of any DW-code is nontrivial of even order.
Proof. Let ![]() be a generator matrix of a DW
be a generator matrix of a DW ![]() -code
-code![]() . We may suppose that all columns of
. We may suppose that all columns of ![]() are
are
nonzero. The ![]() columns of
columns of ![]() are taken among a set of
are taken among a set of ![]() columns. Suppose that all columns of
columns. Suppose that all columns of ![]() are distincts, since
are distincts, since![]() , then the columns of
, then the columns of ![]() are the
are the ![]() distinct nonzero vectors of
distinct nonzero vectors of ![]() and
and ![]() will be the simplex code, which is clearly not DW. This contradiction shows that at least 2 columns of
will be the simplex code, which is clearly not DW. This contradiction shows that at least 2 columns of ![]() are identical. Now the transposition of these two columns gives an automorphism of
are identical. Now the transposition of these two columns gives an automorphism of![]() .
.![]()
We deduce that the dual code ![]() of a DW-code has a non-trivial automorphism group and has minimum distance
of a DW-code has a non-trivial automorphism group and has minimum distance![]() .
.
We consider the general case![]() . The action of automorphism group
. The action of automorphism group ![]() on the set
on the set
![]() of columns of a generator matrix
of columns of a generator matrix ![]() defined by:
defined by: ![]() for all
for all ![]() in
in ![]() and
and
![]() in
in![]() , splits all the columns of
, splits all the columns of ![]() into disjoint orbits. The orbits
into disjoint orbits. The orbits ![]() each formed of a single
each formed of a single
column, they are the columns fixed by the group![]() . We set
. We set ![]() if no orbit is formed of a single
if no orbit is formed of a single
column and then it is clear that ![]() since since
since since ![]() can not be trivial. The
can not be trivial. The ![]() other orbits
other orbits
are![]() ,
, ![]() ,
,![]() . We set
. We set![]() ,
, ![]() if
if ![]() and
and
![]() ,
, ![]() , therefore, we have precisely
, therefore, we have precisely![]() .
.
Up to equivalence, we can consider that the code $mathcal ![]() $ is of generator matrix
$ is of generator matrix
![]()
![]() rows of
rows of![]() , such that
, such that![]() .
.
Since ![]() is a DW-code, then for each
is a DW-code, then for each ![]() for each
for each ![]() we have
we have ![]()
![]() . So
. So ![]() we have
we have![]() . We therefore deduce that:
. We therefore deduce that:![]() ,
,
![]() . So each orbit
. So each orbit ![]() consists of
consists of ![]() equal columns.
equal columns.
The following theorem legitimate the idea of giving a definition to the 3-tuple
![]() which we call signature of the DW-code and we denote
which we call signature of the DW-code and we denote![]() .
.
We give here the full classification of such a code in several cases.
Theorem 10 If two DW-codes ![]() and
and ![]() are equivalent then they have the same signatures:
are equivalent then they have the same signatures:
![]() .
.
Proof. Let ![]() and
and ![]() two equivalent DW-codes of parameters
two equivalent DW-codes of parameters![]() . So
. So ![]() such as
such as![]() .
.
We have![]() . Let
. Let ![]() be a generator matrix of the code
be a generator matrix of the code![]() . Under the action of the
. Under the action of the
automorphism group ![]() we can assume that
we can assume that ![]() is of the form
is of the form ![]() where
where
![]()
![]()
![]() ,
,![]() and
and ![]() .
.
So we have ![]() and then
and then
![]() which is an orbit of the column
which is an orbit of the column ![]() under the action of
under the action of ![]() on
on
the generator matrix ![]() of the code
of the code![]() . similarly we have
. similarly we have ![]()
which is an orbit of the column ![]() under the action of
under the action of ![]() on the generator matrix
on the generator matrix![]() . Thus
. Thus ![]()
and ![]() have the same number of ponctual orbits, the same number of non-ponctual orbits and the two orbits
have the same number of ponctual orbits, the same number of non-ponctual orbits and the two orbits
![]() and
and ![]() on the one hand and
on the one hand and ![]() and
and ![]() on the other hand have the same number of columns. we
on the other hand have the same number of columns. we
conclude that the two codes ![]() and
and ![]() have the same Signature.
have the same Signature.![]()
3.2. Classification
3.2.1. Case 1: ![]() and
and ![]()
We have
![]()
Theorem 11 If ![]() is an
is an ![]() DW-code without punctual orbits
DW-code without punctual orbits ![]() and if the number of non
and if the number of non
punctual orbits is equal to the dimension of the DW-code ![]() then the code
then the code ![]() is equivallent to a DW-
is equivallent to a DW-
code of generator matrix
![]() whith
whith ![]() and t1 = d is the minimal distance of
and t1 = d is the minimal distance of
![]() .
.
Proof. After a series of permutations and elementary operations on rows of ![]() we can make the first line of
we can make the first line of
the first orbit formed only by ones and all other rows are null ![]() all other bits of the first row of the
all other bits of the first row of the
generator matrix are zero. Otherwise the first line of another orbit ![]() will be formed only by 1 s. And a series
will be formed only by 1 s. And a series
of permutations and elementary row operations can make null all the other rows of this orbit so![]() .
.
This is a contradiction since two orbits are disjoint. We obtain a generator matrix of an equivalent code denoted
by the same sign![]() . It is easy to see that
. It is easy to see that ![]() is a generator matrix of a DW-code
is a generator matrix of a DW-code
without punctual orbits ![]() and the number of orbits is equal to the dimension of this DW-code
and the number of orbits is equal to the dimension of this DW-code
![]() and This allows for reasoning by induction. We obtain a generator matrix of an equivalent code
and This allows for reasoning by induction. We obtain a generator matrix of an equivalent code
![]() .
.
It is clear that we have![]() ,
,![]() ,
, ![]() ,
,![]() and
and![]() ,
, ![]()
![]()
since ![]() implies the existence of a punctual orbit
implies the existence of a punctual orbit![]() .
.![]()
Remark 12 In this case, up to equivallence, each ![]() DW-code admits the system
DW-code admits the system ![]() as
as
orthogonal basis:![]() ,
, ![]() ,
, ![]() ,
, ![]() such as
such as
![]() ,
,![]() ,
,![]() ,
, ![]() and
and![]() .
.
Example 13 Consider the ![]() DW-code of generator matrix
DW-code of generator matrix
![]() . It is equivallente to the code of generator matrix
. It is equivallente to the code of generator matrix ![]()
![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]()
Corollary 14 Let two ![]() DW-codes
DW-codes ![]() and
and ![]() without punctual orbits and the number of their orbits
without punctual orbits and the number of their orbits
is equal to their dimension. Then the codes ![]() and
and ![]() are equivallent if and only if
are equivallent if and only if![]() .
.![]()
The converse of Theorem 11 is true under an additional condition.
Theorem 15 Let ![]() an
an ![]() code of generator matrix
code of generator matrix ![]()
![]() as in the last remark
as in the last remark![]() . If:
. If:![]()
![]()
![]()
![]() ,
, ![]() ,
, ![]() we have
we have ![]()
then ![]() is a DW-code of minimum distance
is a DW-code of minimum distance ![]() for which
for which ![]() and
and![]() .
.
Proof. Clear.
Corollary 16 The number of equivalence classes of ![]() DW-codes such as
DW-codes such as![]() ,
, ![]() and
and
![]() equals the number of solutions
equals the number of solutions ![]() of the Diophantine equations
of the Diophantine equations ![]()
satisfying the following conditions
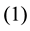
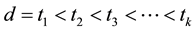
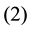

![]() ,
,![]() ,
, ![]() ,
,![]() .
.
Proof. Let the application that maps each equivalence class represented by the matrix ![]() to the
to the
t-tuple ![]() solution of the Diophantine equation as described in Theorem 11. This application is
solution of the Diophantine equation as described in Theorem 11. This application is
clearly a bijection between the set of equivalence classes and the set of solutions of the Diophantine equation satisfying conditions (1) and (2).![]()
3.2.2. Case 2: ![]() and
and ![]()
Theorem 17 If ![]() is an
is an ![]() DW-code with
DW-code with ![]() punctual orbits
punctual orbits ![]() and if the number of non
and if the number of non
punctual orbits is equal to the dimension of the DW-code ![]() then the code
then the code ![]() is equivallent to the
is equivallent to the
DW-code of generator matrix ![]() with
with ![]() and
and
![]() .
.![]()
Example 18 Consider the ![]() DW-code
DW-code ![]() of generator matrix
of generator matrix
![]() . It is equivallente to the code
. It is equivallente to the code ![]() of generator matrix
of generator matrix![]()
![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]()
We have ![]() since
since ![]() and
and ![]() are equivallente.
are equivallente.
The converse of this theorem is true under an additional condition. Let ![]() an
an ![]() of generator matrix
of generator matrix
![]() with:
with: ![]() and
and![]() .
. ![]() are f different
are f different
columns which are also different from all unitary columns![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
For each![]() , denote by
, denote by ![]() the weight of the sum of all the jth rows where
the weight of the sum of all the jth rows where ![]() of the
of the
![]() matrix
matrix
![]()
![]()
For all ![]() denote by
denote by ![]() the weight of the ith row of the
the weight of the ith row of the ![]() matrix
matrix![]() . So by
. So by
setting the numbers ![]() we have the following result, let
we have the following result, let ![]() an
an ![]() code of generator matrix
code of generator matrix
![]() as described in theorem 17 we have:
as described in theorem 17 we have:
Theorem 19 If for all![]() , for all
, for all ![]() and for all
and for all![]() ,
, ![]() we have
we have
![]() then the code
then the code ![]() is a DW-code.
is a DW-code.![]()
Let ![]() an
an ![]() DW-code such as
DW-code such as![]() ,
, ![]() and
and![]() . We have
. We have ![]()
different way to the choice of ![]() fixed columns. For each value of
fixed columns. For each value of ![]() and for the
and for the ![]() -th choice of
-th choice of ![]() fixed
fixed
columns we denote by![]() ,
, ![]() the number of solutions of the Diophantine equations
the number of solutions of the Diophantine equations
![]() which satisfy the following conditions
which satisfy the following conditions
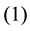
![]()
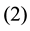
![]()
![]() ,
,![]() ,
,![]() ,
,![]()
So we have the following result.
Theorem 20
![]() The number of equivalence classes of
The number of equivalence classes of ![]() DW-codes with
DW-codes with ![]() and a given
and a given ![]() such that
such that
![]() and
and ![]() equals the number
equals the number![]() .
.
![]() The number of equivalence classes of
The number of equivalence classes of ![]() DW-codes with
DW-codes with![]() ,
, ![]() and
and ![]() equals
equals
the number![]() .
.![]()
Example 21 By using the result of the last theorem and the Q-extension software, We show that there exist
Only 4 ![]() DW-code up to equvallence verifying
DW-code up to equvallence verifying![]() . Indeed
. Indeed ![]() and we have:
and we have:
・ For ![]() the set of possible columns taken in the following order are:
the set of possible columns taken in the following order are:
![]()
![]() ,
,
So the number of DW-codes with![]() ,
, ![]() and
and ![]() is
is![]() .
.
・ For ![]() the set of possible columns taken in the following order are:
the set of possible columns taken in the following order are:
![]()
![]()
So there is no DW-codes with![]() ,
, ![]() and
and ![]() since
since![]() .
.
・ For ![]() the set of possible columns taken in the following order are:
the set of possible columns taken in the following order are:
![]()
![]()
So there is no DW-codes avec![]() ,
, ![]() and
and ![]() since
since![]() .
.
・ For ![]() the set of possible columns taken in the following order are:
the set of possible columns taken in the following order are:
![]()
![]() ,
,![]() ,
,![]() ,
,![]() .
.
So there is one DW-codes such as![]() ,
, ![]() and
and ![]() since
since![]() .
.
We deduce that there is only four ![]() DW-codes, among 98 equivalence classes, satisfying
DW-codes, among 98 equivalence classes, satisfying ![]()
since
![]()
3.2.3. Case 3: ![]() and
and ![]()
We have necessarily![]() .
.
Theorem 22 If ![]() is an
is an ![]() DW-code without punctual orbits
DW-code without punctual orbits ![]() and if the number of non punc-
and if the number of non punc-
tual orbits is different from the dimension of the DW-code ![]() then
then
![]() and the code
and the code ![]() is equivallent to the DW-code of generator matrix
is equivallent to the DW-code of generator matrix
![]()
with![]() .
.![]()
Example 23 The ![]() DW-code of generator matrix
DW-code of generator matrix ![]() is equivallent to the code
is equivallent to the code
of generator matrix![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.![]()
In this case two DW-codes with the same signature are not necessarily equivalent as shown in the following example:
Example 24 Let ![]() the DW-code of generator matrix
the DW-code of generator matrix ![]() and
and ![]() the DW-code of generator matrix
the DW-code of generator matrix ![]() such as
such as ![]() and
and ![]() are not equivalent and
are not equivalent and
![]() ,
,
![]() .
.
We have![]() .
.
3.2.4. Case 4: ![]() and
and ![]()
We can have two cases ![]() or
or ![]()
Theorem 25 If ![]() is an
is an ![]() DW-code with
DW-code with ![]() punctual orbits
punctual orbits ![]() and if the number of non
and if the number of non
punctual orbits is greater than the dimension of the DW-code ![]() then the code
then the code ![]() is equivallent to the
is equivallent to the
DW-code of generator matrix ![]() with
with![]() .
.![]()
Example 26 The ![]() DW-code of generator matrix
DW-code of generator matrix ![]() is equivallent to the code
is equivallent to the code
of generator matrix ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Theorem 27 If ![]() is an
is an ![]() DW-code with
DW-code with ![]() punctual orbits
punctual orbits ![]() and if the number of non
and if the number of non
punctual orbits is lower than the dimension of the DW-code ![]() then the code
then the code ![]() is equivallent to the DW-code of generator matrix
is equivallent to the DW-code of generator matrix
![]()
with![]() .
.![]()
Example 28 The ![]() DW-code of generator matrix
DW-code of generator matrix ![]() is equivallent to the code
is equivallent to the code
of generator matrix ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
. ![]()
Remark 29 Self-orthogonality.
A code which is equivalent to a self-orthogonal code is also self-orthogonal. The property of self- ortho- gonality is then an invariant of the equivalence of codes. We then have the following points:
・ If ![]() or (
or (![]() and
and![]() )then, up to equivalence, a generator matrix of the code is of the form
)then, up to equivalence, a generator matrix of the code is of the form ![]() where
where ![]() is not an empty submatrix. If the code is self-othogonal then
is not an empty submatrix. If the code is self-othogonal then![]() . So
. So
![]() and then we have:
and then we have:
![]()
![]() and
and ![]() and then
and then ![]()
![]()
![]() and
and ![]() then
then ![]() where
where![]() .
.
![]()
![]() and
and ![]() then
then ![]()
![]() finally
finally ![]() and
and ![]() and then
and then ![]()
・ If ![]() and
and ![]() the code
the code ![]() is self-orthogonal if and only if
is self-orthogonal if and only if ![]() for all
for all![]() .
.![]()
3.3. Determination of the Automorphism Group
Theorem 30 The automorphism group of a ![]() DW-code of signature
DW-code of signature ![]() is isomorphic to
is isomorphic to
the group direct product![]() .
.
Proof. Let ![]() be a generator matrix of the code
be a generator matrix of the code![]() . We can assume that
. We can assume that ![]() is of the form
is of the form
![]() where
where![]() ,
, ![]()
![]() and
and ![]()
![]() .
.
For![]() , let
, let![]() , let
, let ![]() for all
for all![]() . Clearly, the subsets
. Clearly, the subsets
![]() form a partition of
form a partition of![]() . Now let
. Now let![]() .
.
Clearly the ![]() are subgroups of
are subgroups of ![]() and each is isomorphic to
and each is isomorphic to ![]() and
and ![]() for all
for all
![]() . Since forall
. Since forall![]() ,
, ![]() , it follows that the
, it follows that the ![]() are subgroups of
are subgroups of![]() .
.
Now we are going to show that ![]() is the inner direct product
is the inner direct product ![]()
If![]() , and
, and![]() ,
, ![]() , then
, then![]() .
.
Let![]() , then applying this equality to each
, then applying this equality to each ![]() yields
yields![]() ,
,![]() .
.
Now let![]() . Since
. Since![]() , the
, the ![]() are globally invariant under
are globally invariant under![]() . Let
. Let ![]() the permutation
the permutation
defined by![]() , if
, if![]() , and
, and ![]() elswhere. Then it is clear that
elswhere. Then it is clear that![]() , and this finishes the proof.
, and this finishes the proof. ![]()
Example 31
・ Consider the ![]() DW-code of generator matrix
DW-code of generator matrix![]() . It is equivallente to the code
. It is equivallente to the code
of generator matrix ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() and
and
・ Consider the ![]() DW-code of generator matrix
DW-code of generator matrix![]() . It is equivallente to the code
. It is equivallente to the code
of generator matrix ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() and
and ![]()
Acknowledgements
The authors would like to thank the refrees for their helpful suggestions and remarks.