Differential Transform Method for Some Delay Differential Equations ()
1. Introduction
The differential transform method (DTM) is a semi analytical-numerical technique depending on Taylor series for solving integral-differential equations (IDEs). The method was first introduced by Pukhov [1] for solving linear and nonlinear initial value problems in physical processes. Zhou, at the same time, had also introduced DTM to study electrical circuits [2] . Since the main advantage of this method is that it can be applied directly to nonlinear ordinary and partial differential equations without requiring linearization, discretization or perturba- tion, it has been studied and applied during the last two decades widely. DTM has been used to obtain numerical and analytical solutions of ordinary differential equations [3] , partial differential equations [4] , eigenvalue pro- blems [5] , differential algebraic equations [6] [7] , integral equations [8] and so on.
Delay differential equations (DDEs) arise in many applied fields, such as control technology, communication networks, and biological population management, and hence they have attracted considerable attention. There are many papers devoted to the problem of approximate solution of DDEs [9] - [15] . Recently, F. Karako and H. Bereketoğlu [13] extend the method of differential transformation for solving the following two types of DDEs:
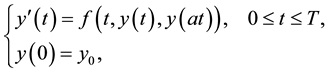 (1)
(1)
and
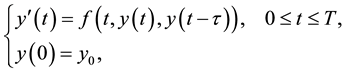 (2)
(2)
with 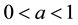 and
and 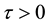 and the constant
and the constant .
.
It should be pointed out that the solution to DDEs (2) maybe be non-unique (see Section 2 in [16] ). So usually, researchers pay more attention to the following DDEs, instead of (2)
 (3)
(3)
where 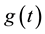 is a given function, called initial function.
is a given function, called initial function.
In this paper, we will apply DTM to find the analytic solution to DDEs (3) with the help of the computer algebra system Mathematica. Thus, in some sense, our work can be viewed as a supplement to [13] .
2. Differential Transform
The basic theory of differential transform can be found in [1] [2] , in this section we will state it in brief.
Consider a function 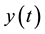 be analytic in the time domain
be analytic in the time domain , and let
, and let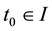 . The function
. The function 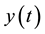 is then
is then
represented by one series whose center is located at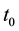 . The differential transform of the function
. The differential transform of the function 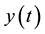 is the form
is the form
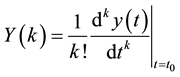 (4)
(4)
where 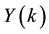 is the transformed function of the original function
is the transformed function of the original function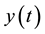 .
.
Differential inverse transformation of ![]() is defined as follows:
is defined as follows:
![]() (5)
(5)
From (4) and (5), it is easy to see that the concept of the differential transformation is derived from the Taylor series expansion. By our assumption, ![]() is taken as zero, then the function
is taken as zero, then the function ![]() is expressed by a finite series and (5) can be written as
is expressed by a finite series and (5) can be written as
![]()
In this study, we use the lower case letters to represent the original functions and upper case letters to stand for the transformed functions (T-functions). The fundamental mathematical operations performed by differential transform method are listed in Table 1.
3. DTM for DDEs (3)
There are many methods to deal with the delay differential Equation (3). For example, linear multistep (LM) methods, Runge-Kutta (RK) methods, waveform relaxation (WR) methods, etc. However, the basic idea to solve the DDE (3) is to solve the following system of ODEs step by step:
![]() (6)
(6)
with![]() . In brief, this idea is to shift the interval from
. In brief, this idea is to shift the interval from ![]() to
to ![]() and extend the solution from
and extend the solution from ![]() to
to ![]() by using the component in the current interval. This procedure can, in
by using the component in the current interval. This procedure can, in
principle, be continued as far as desired. It is called, quite naturally, the method of steps [16] .
Using the basic idea of the method of steps, first, we apply the DTM to find the solution to the following ODEs:
![]()
with![]() .
.
Suppose the approximate solution is given by
![]()
If![]() ,
, ![]() is the solution to (3). Otherwise, we should continue to find the solution in the interval
is the solution to (3). Otherwise, we should continue to find the solution in the interval![]() . At this time, we should solve the following ODEs
. At this time, we should solve the following ODEs
![]()
Applying the DTM to the differential equation above again, we will obtain the following solution
![]()
Of course, we should go on if ![]() holds also. In generally, applying the DTM to ODEs (6), we can obtain the analytic solution
holds also. In generally, applying the DTM to ODEs (6), we can obtain the analytic solution
![]()
until for some![]() ,
,![]() . In fact, after necessary steps, we have the following solution to (3)
. In fact, after necessary steps, we have the following solution to (3)
![]()
Remark 1 If![]() , we can conclude that
, we can conclude that ![]() is the analytic solution to (3) directly.
is the analytic solution to (3) directly.
Remark 2 If ![]() for some integer
for some integer![]() , we can conclude that the analytic solution (3) is
, we can conclude that the analytic solution (3) is
![]()
Remark 3 If we want to improve the accuracy of the approximate solution in each interval, we can combine the above method with the multi-step method given by [17] .
Remark 4 In fact, the DTM based on the method of steps can also be applied to solve the following neutral delay differential equations
![]()
4. Numerical Experiments
In this section, four examples are given to show the performance of the DTM based on the method of steps. First, we want to solve the following simple but classical DDE to further illustrate the process of DTM.
Example 4.1 Consider the DDE [18]
![]() (7)
(7)
First, since![]() , we apply the DTM to obtain the solution in the interval
, we apply the DTM to obtain the solution in the interval![]() . In this interval, (7) can be written as
. In this interval, (7) can be written as![]() , and the initial condition is
, and the initial condition is![]() . Taking the differential transform, we have
. Taking the differential transform, we have
![]()
It is easy to get
![]()
Thus we have the analytic solution ![]() of (7) defined on
of (7) defined on![]() .
.
Second, we should continue to solve the following DDE:
![]()
or equivalently,
![]() (8)
(8)
with initial condition![]() .
.
From (8), we have the following differential transform
![]()
It is easy to get
![]()
Thus we have the analytic solution
![]()
Now, if we want to obtain the solution in the interval [2, 3], we should deal with the following DDE:
![]()
or equivalently,
![]()
with the initial condition![]() .
.
Then we have the following differential transform
![]()
and get
![]()
Thus the analytic solution defined on [2, 3] is given by
![]()
The DTM can be proceed till the desire solution is obtained.
Example 4.2 Consider the nonlinear DDE of third-order [11] [13]
![]() (9)
(9)
Since![]() , according to the foregoing, we have the following ODE, defined in the interval [0, 0.3]
, according to the foregoing, we have the following ODE, defined in the interval [0, 0.3]
![]()
Thus, applying DTM to the equation above, we obtain
![]()
The initial conditions lead to![]() ,
, ![]() , and
, and![]() . It is easy to have
. It is easy to have![]() . Thus we have the solution
. Thus we have the solution
![]()
Noting that![]() , Remark 1 tells us
, Remark 1 tells us ![]() is the analytic solution to (9) in the whole interval
is the analytic solution to (9) in the whole interval![]() .
.
Remark 5 In [13] , F. Karako and H. Bereketoğlu also apply DTM to DDE (9) where the initial function![]() ,
, ![]() is omitted, i.e.
is omitted, i.e.
![]() (10)
(10)
It’s worth pointing out that, using the method given in [13] , only approximate solution can be obtained. On the other hand, for DDEs (3), the initial function has the vital role. Without it, the DDEs may have un-unique
solution. In fact, Example 4.2 shows that ![]() is a solution to (10). Let’s suppose
is a solution to (10). Let’s suppose ![]() is
is
also a solution to (10), then ![]() should satisfy the following DDEs
should satisfy the following DDEs
![]() (11)
(11)
Figure 1 shows the solution to (11), together with it’s first and second derivative value on![]() , with the
, with the
initial function![]() , which satisfies the initial conditions in (10) obviously. It can be seen
, which satisfies the initial conditions in (10) obviously. It can be seen![]() , then
, then ![]() is also the solution to (11). So, (11) has infinite solutions. Maybe, the authors “happen
is also the solution to (11). So, (11) has infinite solutions. Maybe, the authors “happen
to” get the approximate solution of![]() .
.
Example 4.3 Consider a single delay equation with a stiffness parameter [10]
![]() (12)
(12)
with![]() ,
, ![]() ,
,![]() .
.
Similarly, we should solve the following DDE limited in the interval![]() :
:
![]()
Thus applying DTM to this equation, we obtain
![]()
The initial values lead to![]() . With the help of Mathematica, we have
. With the help of Mathematica, we have
![]()
Then, we obtain the solution to (12):
![]()
This is the analytic solution to (12). Particularly, if![]() , then the above solution can be simplified to
, then the above solution can be simplified to![]() , which coincides with the definition on
, which coincides with the definition on![]() . So in this case,
. So in this case, ![]() is the analytic solution to (12) in the whole interval
is the analytic solution to (12) in the whole interval![]() .
.
As the last example, we apply the DTM based on the method of steps to solve a neutral delay differential equations.
Example 4.4 Consider the neutral delay differential equation
![]() (13)
(13)
with the initial function![]() ,
, ![]()
According to the idea of the method of steps, DDE (13) becomes
![]()
Applying DTM to this equation, we have
![]()
From the initial function, we get![]() , so
, so![]() . With the help of Mathematica, we have
. With the help of Mathematica, we have
![]()
Then, the solution to (13) is
![]()
5. Conclusion
Although the theory of differential transform method is not complete yet, it has been successfully applied to solve ordinary differential equations, partial differential equations, integral-differential equations, differential- algebraic equations and etc. In this paper, we apply DTM based on the method of steps to solve some delay differential equations, including neutral delay differential equations, successfully. Numerical experiments show that DTM is feasible and efficient for them. We believe that the operations of DTM presented in this paper also can be used to solve some partial delay differential equations (PDDEs), which is worth while studying in the future work.
Acknowledgements
This work is supported by the National Natural Science Foundation of China, contract/grant number 11371198 and 11401296, Jiangsu Provincial Natural Science Foundation of China, contact/grant no. BK20141008, Natural Science Fund for colleges and universities in Jiangsu Province contact/grant no. 14KJB110007, Jiangsu Provin- cial Key Laboratory for Numerical Simulation of Large Scale Complex Systems contract/grant number 201305 and 201401.