1. Introduction
Mathematical morphology is the theory and technique for the analysis and processing of geometrical structures, based on set theory, lattice theory, topology, and random functions. We consider classical mathematical mor- phology as a field of nonlinear geometric image analysis, developed initially by Matheron [1] , Serra [2] and their collaborators, which is applied successfully to geological and biomedical problems of image analysis. The basic morphological operators were developed first for binary images based on set theory [1] [2] inspired by the work of Minkowski [3] and Hadwiger [4] . They were implemented for gray level images based on local min/max operators and level sets [2] [5] or on fuzzy sets [6] [7] . They were also implemented for gray level images with weighted min/max operators using a geometric interpretation based on the umbra approach of Sternberg [8] [9] which was algebraically equivalent to maxplus convolutions.
In the development of mathematical morphology in the mid-1960s by Georges Matheron and Jean Serra, they heavily stressed the mathematical formalism on mathematical morphology, and in the work of Haralick, Sternberg and Zhuang [10] , the algebraic structure of morphological operators was given.
In this paper, we outline in details the mathematical morphological operators and their algebraic structures when they are linked with union and intersection. We show that the partitioning of structural element before morphological operations is possible.
2. Preliminaries
2.1. Definitions
The following definitions are important for our purpose.
2.1.1. Dilation
Let the image set X and the structuring element B be subsets of the discrete space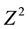 :
: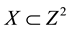 ,
,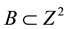 . The
. The
dilation of X by B is defined as ; or the Dilation of a binary image A by
; or the Dilation of a binary image A by
structure element B, is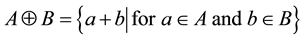 .
.
The dilation transform generally causes image objects to grow in size. From the definitions above, dilation is equivalent to a union of translates of the original image with respect to the structure element, that is,
 .
.
2.1.2. Erosion
Let the image set X and the structuring element B be subsets of the discrete space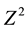 :
: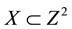 ,
,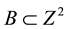 . The
. The
erosion of X by B is defined as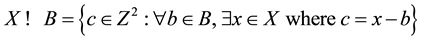 ; or the Erosion of a binary
; or the Erosion of a binary
image A by structure element , is
, is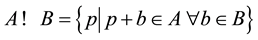 .
.
Similarly erosion transform allows image objects to shrink in size, that is, .
.
2.1.3. Opening
Let the image set X and the structuring element B be subsets of the discrete space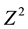 :
: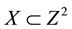 ,
,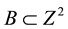 . The
. The
Opening of X by B is defined as![]() ; or the Opening of a binary image A by structure
; or the Opening of a binary image A by structure
element B, is![]() .
.
2.1.4. Closing
Let the image set X and the structuring element B be subsets of the discrete space![]() :
:![]() ,
,![]() . The
. The
Closing of X by B is defined as![]() ; or the Closing of a binary image A by structure element
; or the Closing of a binary image A by structure element
B, is![]() .
.
2.2. Algebraic properties of Dilation and Erosion
We note that Dilation is commutative and associative, that is, ![]() and
and![]() ,
,
where as Erosion is non-commutative and non-associative, that is, ![]() and
and
![]() respectively.
respectively.
Furthermore, Dilation and Erosion are both translation invariant, that is, if ![]() is a vector belonging to A and
is a vector belonging to A and
B (![]() ,
,![]() ), then
), then ![]() and
and![]() . Also both Dilation and
. Also both Dilation and
Erosion are increasing in A, that is, if an image set ![]() is a subset of
is a subset of ![]()
![]() , then
, then ![]()
and![]() . However, Erosion is decreasing in B, that is, if a structuring element
. However, Erosion is decreasing in B, that is, if a structuring element ![]() is a subset of
is a subset of
![]()
![]() , then
, then![]() . Dilation and Erosion transforms are duals of each other, that is,
. Dilation and Erosion transforms are duals of each other, that is,
![]() and
and![]() . Dilation and Erosion are also not the inverse of each other, that is,
. Dilation and Erosion are also not the inverse of each other, that is,
![]() and
and![]() . Both the dilation and erosion transforms have an identity set, I, such
. Both the dilation and erosion transforms have an identity set, I, such
that ![]() and
and![]() . Dilation transform has an empty set, that is,
. Dilation transform has an empty set, that is, ![]() such that
such that![]() .
.
2.3. Algebraic properties of Opening and Closing
We have Opening and Closing transforms as duals of each other, ![]() and
and ![]()
but Opening and Closing are not the inverse of each other, ![]() and
and![]() . Also both
. Also both
Opening and Closing are translation invariant, if x is a vector belonging to A and B, then
![]() and
and![]() . The opening transform is anti-extensive, the
. The opening transform is anti-extensive, the
Opening of A by a structuring element B is always contained in A, regardless of B![]() . The Closing
. The Closing
transform is extensive, the Closing of A by a structuring element B always contains A, regardless of B
![]() .
.
Furthermore, Opening and Closing are both increasing in A. If an image set ![]() is a subset of or equal to
is a subset of or equal to ![]()
![]() , then
, then ![]() and
and ![]() but only Opening is decreasing in B, if a structuring
but only Opening is decreasing in B, if a structuring
element ![]() is a subset of
is a subset of ![]()
![]() , then
, then![]() . Finally, opening and Closing transforms are
. Finally, opening and Closing transforms are
both idempotent, ![]() and
and![]() . However if X is unchanged by opening with B, X is
. However if X is unchanged by opening with B, X is
said to be open, whereas if X is unchanged by closing with B, X is said to be closed.
3. Results
In this section we present unions and intersections of Dilation, Erosion, Opening and Closing of two different sets and their extensions. The following theorems and their proofs will help us to describe the various results.
The morphological operators with n distinct sets
Theorem 1 (The union of Dilation with n differents sets)
If ![]()
Then ![]()
Proof.
If ![]()
Then
![]()
This implies ![]()
Assume that if ![]()
Then ![]()
Now we show that if ![]()
Then
![]()
Theorem 2 (The intersection of Dilation with n different sets)
If ![]()
Then ![]()
Proof.
If ![]()
Then
![]()
This implies ![]()
Assume that if ![]()
Then ![]()
Now we show that if ![]()
Then
![]()
Theorem 3 (The union of Erosion with n distinct sets)
If ![]()
Then ![]()
Proof.
If ![]()
Then
![]()
This implies ![]()
Assume that if ![]()
Then ![]()
Now we show that if ![]()
Then
![]()
Theorem 4 (The intersection of Erosion with n distinct sets)
If ![]()
Then ![]()
Proof.
If ![]()
Then
![]()
This implies ![]()
Assume that if ![]()
Then ![]()
Now we show that if ![]()
Then
![]()
Theorem 5 (The union of Opening with n different sets)
If ![]()
Then ![]()
Proof.
If ![]()
Then
![]()
This implies ![]()
Assume that if ![]()
Then ![]()
Now we show that if ![]()
Then
![]()
Theorem 6 (The intersection of Opening with n different sets)
If ![]()
Then ![]()
Proof.
If ![]()
Then
![]()
This implies ![]()
Assume that if ![]()
Then ![]()
Now we show that if ![]()
Then
![]()
Theorem 7 (The union of Closing with n distinct sets)
If ![]()
Then ![]()
Proof.
If ![]()
Then
![]()
This implies ![]()
Assume that if ![]()
Then ![]()
Now we show that if ![]()
Then
![]()
Theorem 8 (The intersection of Closing with n distinct sets)
If ![]()
Then ![]()
Proof.
If ![]()
Then
![]()
This implies ![]()
Assume that if ![]()
Then ![]()
Now we show that if ![]()
Then
![]()
4. Conclusion
We have shown that Dilation, Erosion, Opening and Closing of two or more sets with the same structural element and carrying out the union of the outcome is the same as taking the union of the two or more sets and operating the results with the structural element. The above result also holds for the intersection. These operators show ways of partitioning the structural element in order to carry out the morphological operation with ease. Further- more, the results above give a simplification of morphological operations when dealing with lots of sets with the same structural element.
Acknowledgements
We are grateful to the Almighty God and the Department of Mathematics, Kwame Nkrumah University of Science and Technology for providing us resources to help complete this research successfully.