Numerical Investigation of a Shock Accelerated Heavy Gas Cylinder in the Self-Similar Regime ()
1. Introduction
When an impulsive acceleration impinges on the corrugated interface between two fluids of different densities, the instability at the interface will arise due to the deposited vorticity induced by the baroclinic torque production term 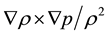 (where
(where 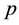 is the pressure and
is the pressure and 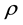 is the density). The class of problems is generally referred to as the Richtmyer-Meshkov (RM) instability [1] [2] . One of the eventual goals in investigating RM instability is to shed light on the resultant mixing. Mixing is of contemporary interest in many fields of research, among which are the inertial confinement fusion [3] , the fuel mixing in a Scramjet [4] , and the explosion of supernovas [5] .
is the density). The class of problems is generally referred to as the Richtmyer-Meshkov (RM) instability [1] [2] . One of the eventual goals in investigating RM instability is to shed light on the resultant mixing. Mixing is of contemporary interest in many fields of research, among which are the inertial confinement fusion [3] , the fuel mixing in a Scramjet [4] , and the explosion of supernovas [5] .
In the RM instability researches, an interesting configuration is a shock wave interacting with a cylindrical interface (circular interface in two dimensions) between two fluids. When a planar shock wave impacts on a heavy gas (e.g., SF6) cylinder around by an ambient gas (e.g., air), a shock wave is reflected and a refracted shock wave transmits into the heavy gas cylinder. Because the heavy gas acoustic impedance exceeds that of the ambient gas, the refracted shock is slower than the incident shock wave, and a convergent shock refraction pattern occurs. Because of this and the curvature of the cylinder, the transmitted shock focuses at the downstream vertex. This focusing will induce a pressure rising that eventually leads to a cusp-like protrusion [6] . The baroclinically deposited vorticity due to the shock-cylinder interaction stretches and distorts the interface and rolls up into a counter-rotating vortex pair. Then, the evolution of the interface will be dominated by the vortex pair and falls into a self-similar regime, which is in some ways similar to the roll-ups of a vortex sheet [7] - [9] .
The propagation of a shock wave in an inhomogeneous medium, and the response of the medium to impulsive acceleration are of fundamental interest in astrophysical systems. The evolution of the interstellar medium in spiral galaxies is significantly influenced by the strong shock waves generated by supernovae explosion [10] . Moreover, it is well-known that the generated shock waves remarkably alter the morphology of the cloud (a region of higher density). The bright eastern knot of the Puppis A supernova remnant results in a distorted shock front due to a cloud-shock interaction as seen in images from the Chandra X-ray telescope [11] . In this paper, the shock-cylinder interaction is a particularly simple configuration to investigate the problem of shock accelerated inhomogeneous flows.
There are many experimental and numerical researches of the shock-cylinder interactions which concentrate on different subjects. Haas and Sturtevant [12] , Jacobs [13] and Tomkins et al. [14] studied this problem experimentally for exploring the wave patterns and the distortion of volume in the RM instability, studying the effects of centrifugal force and viscosity, and investing the mixing mechanisms in a shock-accelerated flow, respectively. Based on the experiments performed by Haas and Sturtevant, Picone and Boris [15] studied the early and the late time phenomena of these experiments numerically. Additionally, Quirk and Karni [16] also simulated the same experiments with the concentration on the early stages of the shock-cylinder interaction. Recently, in light of the experiment performed by Tomkins et al., Weirs et al. [17] investigated the three dimensional effects and Shankar et al. [18] studied the effect of the tracer particle in the shock cylinder interactions.
As be mentioned just, there were some studies on the shock accelerated heavy gas cylinder, however, in the aforementioned papers no attention has been paid on a perhaps existing scaling law in contrast with the single mode or multi mode RM instability [19] - [21] . Moreover, most numerical studies were performed for validating codes with comparing to the experimental data. In this work, we systemically and meaningfully analyze the obtained numerical results. Comparing with the results from the prediction of vorticity dynamics, we want to present the behavior of the characterized variables in the evolution of the shock accelerated cylinder. Through studying the evolution of the integral length of the shock-accelerated cylinder, we shed light on the scaling law of the growth of the normalized length follows in the self-similar regime.
2. Numerical Methods and Initialization
This paper applies our large eddy simulation code MVFT (multi-viscous flow and turbulence) [22] to simulate the multi-viscosity-fluid and turbulence. The code MVFT is used for the compressible large eddy simulation that was developed by Institute of Fluid Physics at the China Academy of Engineering Physics. MVFT can be used to simulate multi-component flows, and compute shocks, contact discontinuities and material interfaces at high accuracy. It splits the flow into an inviscid flow and a viscous flow by using an operator splitting technique, where the former is computed by employing the piecewise parabolic method with a third-order Godunov scheme and the latter is calculated by utilizing a central difference scheme in conjunction with a second-order Runge- Kutta method for the time integration. MVFT applies based on the piecewise parabolic method [23] to interpolate physical quantities, the Vreman [24] subgrid scale eddy viscosity model to conduct large eddy simulation, and to solve Navier-Stokes equations.
The initial conditions are significantly important in numerical simulations, especially for the membrane less RM instability researches. Initially, a sharp interface [25] [26] was used but leaded to an ill-posed simulation compared with the experiments. This is because the interspecies diffusion would not be deniable in the membrane less technique [27] which is used to form the interface between two fluids in experiments. More concentrations should be required on the interfacial diffusion. Consequently, an interfacial transition layer with finite thickness [28] was introduced to characterize the diffusive interface. Recently, a well-characterized initial concentration profile [17] was specified with experimentally measured data. And the contour map of scalar mass fraction and dissipation rate obtained from numerical calculations with the profile were in a good agreement with experimental data qualitatively. For we will simulate the same experiment, the profile is chosen as our initial concentration profile.
In the present simulations, the initial conditions were adapted to the Mach 1.2 shock tube experiment of Tomkins et al. [14] which was performed at Los Alamos National Laboratory (LANL). Figure 1 shows a schematic of the computational domain. To match the shock tube test section dimensions, the computational domain has 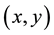 dimension
dimension 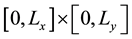 with
with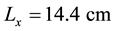 ,
,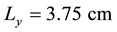 . The inflow/outflow boundary condition is used on the left and right x boundaries. At the upper y boundary, the reflecting boundary condition is used and the symmetry condition is enforced at the lower y boundary. Three different grid resolutions with
. The inflow/outflow boundary condition is used on the left and right x boundaries. At the upper y boundary, the reflecting boundary condition is used and the symmetry condition is enforced at the lower y boundary. Three different grid resolutions with 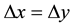
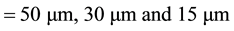 are used for grid convergence study. In the simulations, the initial concentration profile of the cylinder in [17] is used. The simulations are run at a CFL number of 0.2. The main gas parameters are presented in Table 1.
are used for grid convergence study. In the simulations, the initial concentration profile of the cylinder in [17] is used. The simulations are run at a CFL number of 0.2. The main gas parameters are presented in Table 1.
3. Results
Figure 2 depicts the snapshots of the time evolution of the cylinder, which shows volume fraction maps that are corresponding to the densities for seven times after shock passage on three different grid resolutions. Counter rotating vortex pair formed at the interface owing to the baroclinic vorticity deposited stretches and rolls the interface in ward the vortex cores after the shock collides. At about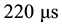 , the vortex pair starts to roll up into the vortex core, and then falls into a self similar state. In Figure 2 one also can see a cusp-like protrusion [6] produced by shock refraction in the simulations with finer grid. This demonstrates that finer grid is needed in the shock-cylinder simulations for better capturing more fine-scale structures.
, the vortex pair starts to roll up into the vortex core, and then falls into a self similar state. In Figure 2 one also can see a cusp-like protrusion [6] produced by shock refraction in the simulations with finer grid. This demonstrates that finer grid is needed in the shock-cylinder simulations for better capturing more fine-scale structures.
Figure 3 presents the negative circulation evolution over time of the flow field. Once a straight vortex sheet rolls up, the circulation of each branch is either positive or negative. For the roll-ups of the straight vortex sheet, we only consider the negative circulation here. The amount of circulation deposited during the interaction of the
![]()
Figure 1. Schematic diagram of the computational domain.
![]()
Table 1. Properties of air and SF6 gases.
![]()
Figure 2. Image sequence of SF6 volume fraction at t = 130, 220, 310, 400, 560, and 650 μs after shock impingement on the coarse (left column), medium (middle column), and fine (right column) mesh resolutions. The shock has traversed the cylinder from top to bottom.
![]()
Figure 3. Negative circulation as a function of time on three different grid resolutions. The short dashed, short dotted and solid lines correspond to the results computed on the coarse, medium, and fine grid resolutions respectively. The dashed line is the theoretical prediction for the negative circulation in [29] .
shock wave with the interface is calculated using a path integration of velocity
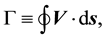 (1)
(1)
where 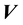 is the velocity vector and
is the velocity vector and ![]() is the path. From Stokes theorem, the circulation is a measure of the vorticity over an area
is the path. From Stokes theorem, the circulation is a measure of the vorticity over an area![]() . In the two dimensional flow, the circulation is
. In the two dimensional flow, the circulation is
![]() (2)
(2)
with
![]() (3)
(3)
where ![]() is the vorticity component which is perpendicular to the x-y plane, u and v are x and y components of the velocity respectively.
is the vorticity component which is perpendicular to the x-y plane, u and v are x and y components of the velocity respectively.
The vorticity generated by a shock wave propagating through a circular cross-section has been studied by Picon and Boris [29] . They gave the magnitude of the vortex strength or circulation,
![]() (4)
(4)
where ![]() is the flow velocity behind the shock in the laboratory frame, W is the shock velocity,
is the flow velocity behind the shock in the laboratory frame, W is the shock velocity, ![]() is the radius of the cross-section of the cylinder,
is the radius of the cross-section of the cylinder, ![]() is the ambient density, and
is the ambient density, and ![]() is the density of the gas in the cylinder. For an initial temperature of 298 K and pressure of 0.8 atm, the resulting 1D gas dynamic velocities are the following,
is the density of the gas in the cylinder. For an initial temperature of 298 K and pressure of 0.8 atm, the resulting 1D gas dynamic velocities are the following, ![]() , and
, and![]() . In the simulations, the effective radius
. In the simulations, the effective radius ![]() is 2.57 mm, the ambient density
is 2.57 mm, the ambient density ![]() is the density of air,
is the density of air, ![]() , and
, and ![]() is the density of the cylinder 2.85 kg/m3. From these data, one can get the amount of circulation is
is the density of the cylinder 2.85 kg/m3. From these data, one can get the amount of circulation is![]() . From Figure 3, one can see that the simulation data is shown a good agreement with the value.
. From Figure 3, one can see that the simulation data is shown a good agreement with the value.
Additionally, one can calculate the vortex strength by applying the approximate model of the compact vortex. When a shock impacts on a heavy gas cylinder, the cylinder will stand here relative to the ambient gas because of its inertia. Then the cylinder will have a velocity ![]() with the opposite shock direction relative to the background. There is a discontinuity of the tangential velocity at both edge of the cylinder, so the cylinder could be considered as a two dimensional vortex sheet. From the vorticity dynamics, one can calculate the magnitude of the circulation of the compact vortex rolled up from the vortex sheet
with the opposite shock direction relative to the background. There is a discontinuity of the tangential velocity at both edge of the cylinder, so the cylinder could be considered as a two dimensional vortex sheet. From the vorticity dynamics, one can calculate the magnitude of the circulation of the compact vortex rolled up from the vortex sheet ![]() [30] . One can obtain a value of
[30] . One can obtain a value of ![]() which is also in a good agreement with the numerical results.
which is also in a good agreement with the numerical results.
In two dimensional case, as analogous to center of mass, one can define the coordinate of center of vorticity,
![]() (5)
(5)
The time evolution of the center of vorticity is presented in the Figure 4. One can see that the x-component velocity of center of voriticity is 85.6 m/s. In [15] , Picone and Boris gave an equation to compute the perpendicular distance d of the vortex core to the y axis or the half vortex spacing,
![]() (6)
(6)
Here, ![]() is the velocity of center of vorticity in x direction. Then, one can get the value of d, 2.3 mm. From Figure 4, the value is in a good agreement with the center of vorticity in y direction.
is the velocity of center of vorticity in x direction. Then, one can get the value of d, 2.3 mm. From Figure 4, the value is in a good agreement with the center of vorticity in y direction.
The vorticity distribution along y direction computed on the fine mesh resolution at seven different times is shown in Figure 5. The vorticity trends to get together inward and extend outward as time goes by. Because of roll-ups, there are some troughs appeared in the vorticity distribution. After about![]() , the vorticity is almost fixed at the outer edge as time elapses, although it also moves inward to the y axis. The behavior is consistent with the evolution of the center of vorticity in y direction which decreases after about
, the vorticity is almost fixed at the outer edge as time elapses, although it also moves inward to the y axis. The behavior is consistent with the evolution of the center of vorticity in y direction which decreases after about ![]() shown in Figure 4.
shown in Figure 4.
Considering the mole fraction![]() , the spatial maximum of the mole fraction in the stream wise direction gives
, the spatial maximum of the mole fraction in the stream wise direction gives
![]()
Figure 4. Center of vorticity in x direction (solid line) and y direction (shot dot) as a function of time computed on the fine grid resolution. The dashed line is obtained from linear fitting. The dash dot line corresponds to the theoretical prediction for the half of vortex spacing in [29] .
![]()
Figure 5. Vorticity distribution along y direction at seven different times on the resolution of![]() .
.
![]() (7)
(7)
The left and right edge locations of the cylinder, ![]() and
and![]() , are defined as the x position
, are defined as the x position![]() , with
, with ![]() in the present simulations. The length is given by
in the present simulations. The length is given by![]() ; which divided by the diameter of the cylinder
; which divided by the diameter of the cylinder![]() , then one can get the normalized length
, then one can get the normalized length![]() . In Figure 6, the log-log plot of normalized length vs. time shows that from about
. In Figure 6, the log-log plot of normalized length vs. time shows that from about ![]() to
to![]() , there is a linear relationship. Then, a power law of
, there is a linear relationship. Then, a power law of ![]() for the normalized length is obtained.
for the normalized length is obtained.
4. Discussions and Conclusions
To the authors’ knowledge, there hasn’t been an investigation of the power law of the length for a shock accelerated gas cylinder, although the power law followed by the mixing zone width has been investigated in the single mode or multi-mode Richtmyer-Meshkov instability. Dimonte and Schneider [19] reported a power law ![]()
![]()
Figure 6. Log-plot of normalized length vs. time computed on the coarse (shot dashed line), medium (short dotted line) and fine (solid line) mesh resolutions. The dashed line corresponds to the power law of![]() . The scattered data correspond to the experimental data obtained from [14] .
. The scattered data correspond to the experimental data obtained from [14] .
with ![]() for
for ![]() with linear electric motor experiments in three dimensions. Using full numerical simulations, Oron et al. [20] gave the power exponent
with linear electric motor experiments in three dimensions. Using full numerical simulations, Oron et al. [20] gave the power exponent ![]() for the bubbles. Recently, Sohn [21] predicted that the bubble fronts follow a power law with
for the bubbles. Recently, Sohn [21] predicted that the bubble fronts follow a power law with ![]() in the range of
in the range of ![]() by applying a quantitative model of bubble completion. For the roll-ups of vortex sheet, the power law of
by applying a quantitative model of bubble completion. For the roll-ups of vortex sheet, the power law of ![]() with
with ![]() has been gained [7] , where
has been gained [7] , where ![]() is the polar radius of the spiral. Interestingly, it is seen that the power law exponent of the normalized length obtained here is almost same to that of the bubble fronts in [20] , although it’s quite different from the others.
is the polar radius of the spiral. Interestingly, it is seen that the power law exponent of the normalized length obtained here is almost same to that of the bubble fronts in [20] , although it’s quite different from the others.
In conclusion, we studied the evolution of a shock impinging heavy gas cylinder and the growth of the normalized length. A self-similar behavior is shown from the snapshots of the evolution of the gas cylinder. The two dimensional numerical results of the negative circulation, the center of vorticity, and the vortex spacing are in a good agreement with the results obtained from the analyses of Picon and Boris [29] . Moreover, the normalized length obeys a power law ![]() with
with![]() . Whether the power law is a universal property for a shock accelerated cylinder is under investigation. More investigations of a shock accelerated cylinder with different radii, density ratios, and Mach numbers will be performed in future.
. Whether the power law is a universal property for a shock accelerated cylinder is under investigation. More investigations of a shock accelerated cylinder with different radii, density ratios, and Mach numbers will be performed in future.
Acknowledgements
This work was sponsored by the National Science Foundation of China under Grants No. 11202195 and No. 11072228 and the Science Foundation of the China Academy of Engineering Physics under Grants No. 2011B0202005 and No. 2011A0201002.