Quantification of Revenue Induction and Expenditure Reflux in a Monetary Economy ()
1. Introduction
Expended money becomes revenue for somebody. Since money is an entity which continues to circulate, received money is expended and again becomes revenue for somebody. Further, that received money is also expended, and again becomes revenue for somebody. In this manner, expenditure induces revenue for each agent in a monetary economy. We call this the revenue induction phenomenon.
Moreover, a portion of agents who receive in the above case may be an agent who originally expended. In other words, part of the expenditure by an agent can return as their own revenue. This special case of revenue induction is called the expenditure reflux phenomenon in this paper.
Expenditure reflux is a natural conclusion of money circulation. Therefore, its existence was recognized in the olden days by economists who considered money circulation. François Quesnay, who was known as a pioneer that researched economic circulation through devising Tableau Économique, said:
“Thus of the 1200 livres’ worth of product, 600 are consumed by this class1, and its advances of 600 livres are returned to it in the form of money through the sales which it makes to the proprietor and to the sterile expenditure class.”2
Apart from this example, qualitative recognitions of revenue induction and expenditure reflux are often seen. The multiplier effect can be interpreted as a quantification of the revenue induction3, but it is not a sufficiently precise quantification especially for that of the expenditure reflux. The purpose of this paper is to quantify these phenomena more precisely.
Regarding the quantitative expression of a monetary economy, the author already wrote Miura [35] . This paper shares basic frameworks with that paper. We will reconfirm them.
We decide that a target group of economic agents for description is called the relevant society.4 There are various kinds of agents, such as an individual, a family, a corporation, the government, and so on. However, this paper does not consider the differences between such kinds of agent. We treat all agents merely as agents in the group. We denote the relevant society by Set N. Moreover, we decide that a target term for description is called the relevant term. We assume that the relevant term is finite. This assumption is rewritten so that the relevant term always has a beginning and an end. The sphere that satisfies both the relevant society and the relevant term is called the relevant space-time.
Furthermore, we do not distinguish between various types of transfer of money, including purchase of commodity, payment of wage, financial relation, donation, and so on. Also, there are various kinds of money such as the dollar, pound, euro, yen, and so on. However, in this paper, we assume that money in the relevant space-time is of only one kind.
We define expenditure as transferring money to the relevant space-time, and revenue as money being transferred from the relevant space-time. There is a possibility that a transfer of money occurs between the relevant society and its outside, but transferring money to the outside is not called expenditure and money being transferred from the outside is not called revenue in this paper.
Moreover, we decide that the sources excluding revenue, such as possession at term beginning, production and being transferred from the outside of the relevant society, are collectively called the beginning money. Also, we decide that the results excluding expenditure, such as possession at term end, disappearance and transferring to the outside of the relevant society, are collectively called the end money.
Let 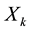 be the expenditure quantity of Agent
be the expenditure quantity of Agent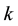 ;
;  be the revenue quantity of Agent
be the revenue quantity of Agent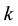 ;
;  be the quantity of the beginning money of Agent
be the quantity of the beginning money of Agent ; and
; and 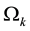 be the quantity of the end money of Agent
be the quantity of the end money of Agent . By their economic meaning, these are all non-negative.
. By their economic meaning, these are all non-negative.
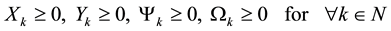 . (1)
. (1)
Further, we suppose that expenditure of any agent is positive to simplify description. Using symbols, the supposition is expressed as follows.
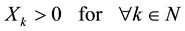 . (2)
. (2)
Then, we have confirmed that the sum of gross source of any agent and the sum of gross result of the same agent are equal. We have named this proposition the law of gross disposal.5 Using symbols, the law is denoted as follows.
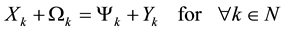 . (3)
. (3)
Moreover, we have defined the expenditure rate and confirmed its range as follows.6
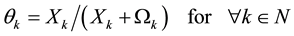 . (4)
. (4)
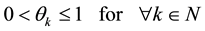 . (5)
. (5)
Note that the quantitative expression of the expenditure reflux ought to be a relational formula between expenditure and revenue of the same agent. Such a formula can easily be derived from past settings. If we substitute Equation (3) in Equation (4), we can derive
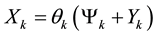 . (6)
. (6)
This is certainly a relational formula between expenditure and revenue of the same agent. However, it is not a formula which denotes expenditure reflux.
In a monetary economy, there are two relationships between expenditure and revenue of the same agent. One is the expenditure reflux, and the other is the circular disposal. The latter refers to a flow of money from revenue to expenditure inside of only one agent.7 On the other hand, the former refers to a flow of money from expenditure to revenue via the outside of an agent.
It is natural that two flows between expenditure and revenue exist in monetary economy. If there existed only one of the two flows, money would flow in only one direction and could not circulate. Both flows are required to fulfill money circulation.
Although Equation (6) is a valid relational formula, it represents the percentage of expenditure in the gross source. It is a quantitative expression of the circular disposal. Thus, we call this the circular disposal formula. It expresses the flow from revenue to expenditure, but not the expenditure reflux, which is the flow from expenditure to revenue. We have to find another relational formula for its quantification.
Note that we have formed a money circulation equation in Miura [35] . The pioneer of the equation is Mária Augustinovics in Hungary8, and the current author showed its modification in that paper. Both expenditure and revenue have been derived as a solution of the equation. Therefore, it is possible to obtain a relational formula between expenditure and revenue of the same agent by using those solutions. However, since the equation is formed with consideration to the whole money circulation, the formula mixes two flows and so cannot express one relationship independently. For the quantification of expenditure reflux, it is not suitable to use a solution of the money circulation equation.9
In order to avoid confusion with inappropriate relational formulas, we first execute the quantification of the revenue induction while carefully ascertaining its adequacy. Based on this, we derive the quantification of the expenditure reflux as its special case.
2. Quantification of the Revenue Induction and the Expenditure Reflux
For convenience, we decide that an agent whose expenditure becomes the initial point of the relationship is called the standard agent. We decide that the standard agent is denoted 0 and the other agents of the standard agent are denoted by the natural numbers from 1 to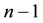 . The relevant society is denoted
. The relevant society is denoted . Further, we denote the set of the other agents
. Further, we denote the set of the other agents![]() .
.
The revenue induction consists of three steps. The first step is that the expenditure of the standard agent causes the revenue of the other agents. The second step is that the revenue of the other agents is disposed to their expenditure. The third step is that the expenditure of the other agents causes the revenue for each agent. We will execute the quantification of each step sequentially.
To start, we quantify the first step where the expenditure of the standard agent causes the revenue of the other agents. Let ![]() be the separate transfer quantity from Agent i to Agent j. From its economic meaning, it is naturally non-negative.
be the separate transfer quantity from Agent i to Agent j. From its economic meaning, it is naturally non-negative.
![]() . (7)
. (7)
We have decided that transferring money to the outside is not called expenditure and money being transferred from the outside is not called revenue in this paper. Hence, the following relations hold.
![]() . (8)
. (8)
![]() . (9)
. (9)
Further, let Agent ![]() be one of the others. The expenditure of the standard agent to the other agent
be one of the others. The expenditure of the standard agent to the other agent ![]() is directly denoted by
is directly denoted by![]() . This is included in a part of the revenue of
. This is included in a part of the revenue of![]() , but the revenue also includes the expenditures from the others. Applying Equation (9) to Agent
, but the revenue also includes the expenditures from the others. Applying Equation (9) to Agent![]() , the gross revenue of
, the gross revenue of ![]() is expressed as
is expressed as
![]() . (10)
. (10)
The quantification of the first step has been completed. We now shift to the second step where the other agents dispose to their expenditure.
As mentioned above, a disposal from revenue to expenditure can be denoted by the circular disposal formula (Equation (6)) through using the expenditure rate. Applying Equation (6) to Agent![]() , the circular disposal formula of
, the circular disposal formula of ![]() is expressed as follows.
is expressed as follows.
![]() . (11)
. (11)
This equation is the quantitative expression of the second step. Substituting Equation (10) in Equation (11), we obtain the quantitative expression of the integration of the first and second step.
![]() . (12)
. (12)
Before shifting to the third step, we recall the definition of the expenditure distribution rate and its range as in Miura [35].10
![]() . (13)
. (13)
![]() . (14)
. (14)
Moreover, by Equations (8) and (13), we can derive
![]() . (15)
. (15)
We now begin the third step where the expenditure of the other agents causes revenue for each agent. Expenditure causes further expenditure because money continues to transfer. We will derive the quantity of expenditure considering this point.
In order to combine the outcome of the first and second step with the third step, we substitute Equation (13) for the case ![]() in Equation (12) provided that
in Equation (12) provided that![]() . Moreover, if we transpose its terms including expenditure except that of the standard agent, we obtain
. Moreover, if we transpose its terms including expenditure except that of the standard agent, we obtain
![]() .
.
We write this formula from ![]() to
to ![]() and regard the results as a system of simultaneous equations in
and regard the results as a system of simultaneous equations in![]() . We call this the partial money circulation equation.
. We call this the partial money circulation equation.
A difference between the partial money circulation equation and the money circulation equation discussed in Miura [35] is that the variables of the former equation are expenditures of all others whereas those of the latter equation are expenditures of all agents. Hereafter, we call the latter the whole money circulation equation in order to distinguish it from the partial equation.
Then, we denote the partial money circulation equation by using a matrix expression.
Let ![]() be an
be an ![]() -dimensional unit matrix;
-dimensional unit matrix; ![]() be an
be an ![]() -dimensional column vector with the ith element equal to
-dimensional column vector with the ith element equal to ![]() excluding
excluding![]() ;
; ![]() be an
be an ![]() -dimensional column vector with the hth element equal to
-dimensional column vector with the hth element equal to ![]() excluding
excluding![]() ;
; ![]() be an
be an ![]() -dimensional column vector with the hth element equal to
-dimensional column vector with the hth element equal to ![]() excluding
excluding![]() ;
; ![]() be an
be an ![]() -dimensional diagonal square matrix with the hth element equal to
-dimensional diagonal square matrix with the hth element equal to ![]() excluding
excluding![]() ; and
; and ![]() be an
be an ![]() -dimensional square matrix with the
-dimensional square matrix with the ![]() th element equal to
th element equal to ![]() excluding
excluding ![]() and
and![]() . The partial money circulation equation is denoted by
. The partial money circulation equation is denoted by
![]() .
.
Note that ![]() is a non-negative matrix because
is a non-negative matrix because ![]() from Equations (5) and (14). Hence,
from Equations (5) and (14). Hence, ![]() is a Z-matrix, which is defined as a square matrix in which the non-diagonal elements are all non-positive. Moreover, we can obtain
is a Z-matrix, which is defined as a square matrix in which the non-diagonal elements are all non-positive. Moreover, we can obtain ![]() from Equations (1), (5) and (7). Considering this with Equation (2), we find that
from Equations (1), (5) and (7). Considering this with Equation (2), we find that ![]() where
where![]() .11 This type of equation has a unique solution if and only if the following condition is satisfied.
.11 This type of equation has a unique solution if and only if the following condition is satisfied.
Let F be a subset of M which is not empty and G be the relative complement of F in N if F is a proper subset. The condition is ![]() such that
such that![]() , or
, or![]() ,
, ![]() such that
such that ![]() for
for![]() .12 By Equations (1), (5) and (7), the former condition is equivalent to
.12 By Equations (1), (5) and (7), the former condition is equivalent to ![]() such that
such that ![]() or
or![]() . By Equations (2), (5) and (13), the latter condition is equivalent to
. By Equations (2), (5) and (13), the latter condition is equivalent to![]() ,
, ![]() such that
such that![]() .
. ![]() such that
such that ![]() or
or![]() ,
, ![]() such that
such that ![]() can be summarized as
can be summarized as![]() ,
, ![]() such that
such that![]() . Therefore, we can see that the partial money circulation equation has a unique solution if and only if
. Therefore, we can see that the partial money circulation equation has a unique solution if and only if ![]() such that
such that ![]() or
or![]() ,
, ![]() such that
such that ![]() for
for![]() .
.
This solvability condition means that any subset of the others satisfies the space-time openness condition for the source direction.13 Since M is a subset of N, these opennesses are satisfied under the disposal irreversibility principle, which means that money can be disposed only from revenue of the past to expenditure of the future.14 Since this principle seems to be valid universally, the unique solution of the partial money circulation equation always exists.
Let ![]() be the
be the ![]() th element of the inverse of
th element of the inverse of![]() . It can be calculated from the expenditure rate and the expenditure distribution rate of all others, and has the following peculiarities.15
. It can be calculated from the expenditure rate and the expenditure distribution rate of all others, and has the following peculiarities.15
![]() . (16)
. (16)
Then, the solution of the partial money circulation equation can be expressed as
![]() . (17)
. (17)
The calculation of the others’ expenditure considering the continuation of expenditure has been completed. Then, we shift to the completion of the third step.
Due to Equations (9) and (13), we can see that
![]() . (18)
. (18)
If we substitute Equation (17) in Equation (18), we obtain
![]() . (19)
. (19)
Note that,
![]()
If we substitute this computation in Equation (19), the equation is rewritten as
![]() . (20)
. (20)
In order to avoid a complication of description, we introduce a new concept. It is defined as
![]() . (21)
. (21)
Since ![]() can be calculated from the expenditure rate and the distribution rate of all others,
can be calculated from the expenditure rate and the distribution rate of all others, ![]() can also be calculated from the expenditure rate and the distribution rate of all others. If we substitute Equation (21) in Equation (20), we can derive
can also be calculated from the expenditure rate and the distribution rate of all others. If we substitute Equation (21) in Equation (20), we can derive
![]() . (22)
. (22)
![]() refers to each revenue and
refers to each revenue and ![]() refer to the separate expenditures of the standard agent. Equation (22) is our searching formula which expresses the revenue induction phenomenon. We call this the revenue induction formula from the standard agent to Agent j.
refer to the separate expenditures of the standard agent. Equation (22) is our searching formula which expresses the revenue induction phenomenon. We call this the revenue induction formula from the standard agent to Agent j.
Then, we think about the revenue induction formula in which Agent j is the standard agent. Using symbols, this is as follows.
![]() . (23)
. (23)
This is nothing but the expenditure reflux formula which we have looked for as a quantitative expression of the expenditure reflux phenomenon. If we rewrite Equation (23) using the expenditure distribution rate of the standard agent (Equation (13)), the expenditure reflux formula is also expressed as follows.
![]() . (24)
. (24)
On the other hand, the circular disposal formula (Equation (6)) in the case ![]() is as follows.
is as follows.
![]() . (25)
. (25)
If we regard Equations (24) and (25) as simultaneous equations in ![]() and
and![]() , we can calculate the expenditure and revenue of the standard agent by the expenditure rate, the distribution rate and the beginning money of all agents. Note that they can be also calculated by solving the whole money circulation equation.16 Equation (24) is derived through solving the partial equation and Equation (25) is included in the whole equation. Therefore, solving the simultaneous equations of these correspond to solving the whole equation using two steps.
, we can calculate the expenditure and revenue of the standard agent by the expenditure rate, the distribution rate and the beginning money of all agents. Note that they can be also calculated by solving the whole money circulation equation.16 Equation (24) is derived through solving the partial equation and Equation (25) is included in the whole equation. Therefore, solving the simultaneous equations of these correspond to solving the whole equation using two steps.
We also interpret this simultaneous equation qualitatively. Equation (24) refers to the flow of money from expenditure to revenue, and Equation (25) refers to the flow of money from revenue to expenditure. Hence, solving the simultaneous equations of these equations is the quantitative unification of the two flows of money circulation. It is the same as solving the whole money circulation equation.
3. Revenue Induction Coefficient and Expenditure Reflux Coefficient
In the revenue induction formula (Equation (22)), the coefficient of ![]() represents the increase of revenue for Agent j induced by one unit increase of expenditure of the standard agent to Agent h unless it causes a variation in the expenditure rate or the distribution rate of any others. We call this the revenue induction coefficient from standard agent to Agent j through Agent h.
represents the increase of revenue for Agent j induced by one unit increase of expenditure of the standard agent to Agent h unless it causes a variation in the expenditure rate or the distribution rate of any others. We call this the revenue induction coefficient from standard agent to Agent j through Agent h.
We examine a concrete expression of the revenue induction coefficient for the case where the Agent j in the formula is the other.
In the case![]() , the revenue induction coefficient is
, the revenue induction coefficient is![]() . Unity in the coefficient is obtained from the expenditure which the standard agent expends to
. Unity in the coefficient is obtained from the expenditure which the standard agent expends to ![]() directly. Therefore, it should be called the direct revenue induction coefficient. On the other hand,
directly. Therefore, it should be called the direct revenue induction coefficient. On the other hand, ![]() in the coefficient is obtained from the expenditure which the others expend to
in the coefficient is obtained from the expenditure which the others expend to ![]() but its distant source is the expenditure of the standard agent. Therefore, it should be called the indirect revenue induction coefficient from standard agent to Agent j through Agent h.
but its distant source is the expenditure of the standard agent. Therefore, it should be called the indirect revenue induction coefficient from standard agent to Agent j through Agent h.
In the case![]() , the revenue induction coefficient is only
, the revenue induction coefficient is only![]() . That is, the revenue induction coefficient is equivalent to the indirect one.
. That is, the revenue induction coefficient is equivalent to the indirect one.
![]() can also be interpreted to represent the increase of revenue for Agent j caused by one unit increase of the beginning money of Agent h. However, we must pay attention that it does not include an effect through the expenditure of the standard agent because the expenditure of the standard agent is externalized in the derivation of the revenue induction formula. All effects, including an effect through the expenditure of the standard agent, are denoted by the solutions of the whole money circulation equation.
can also be interpreted to represent the increase of revenue for Agent j caused by one unit increase of the beginning money of Agent h. However, we must pay attention that it does not include an effect through the expenditure of the standard agent because the expenditure of the standard agent is externalized in the derivation of the revenue induction formula. All effects, including an effect through the expenditure of the standard agent, are denoted by the solutions of the whole money circulation equation.
Next, we examine a concrete expression of the revenue induction coefficient for the case where the Agent j in the formula is the standard agent.
Since Agent h in the expenditure reflux formula (Equation (23)) refers to the other, ![]() holds. Accordingly, the revenue induction coefficient of
holds. Accordingly, the revenue induction coefficient of ![]() is
is![]() . This is nothing but the indirect revenue induction coefficient from the standard agent to themselves through Agent h. Because it expresses the reflux quantity of one unit of expenditure, we call this the expenditure reflux coefficient through Agent h.
. This is nothing but the indirect revenue induction coefficient from the standard agent to themselves through Agent h. Because it expresses the reflux quantity of one unit of expenditure, we call this the expenditure reflux coefficient through Agent h.
Further, ![]() refers to the transfer from the agent to themselves. We call this the self-transfer. The coefficient of the self-transfer is unity. We can also interpret the expenditure reflux coefficient of the self-transfer as always equal to unity.
refers to the transfer from the agent to themselves. We call this the self-transfer. The coefficient of the self-transfer is unity. We can also interpret the expenditure reflux coefficient of the self-transfer as always equal to unity.
The key to examining a concrete quantitative effect of revenue induction is the numerical value of the revenue induction coefficient. Whereas the direct coefficient is fixed to unity, the indirect coefficient can become various values although its range is limited. We will prove some theorems regarding its range, including some relevant lemmas.
Lemma 3.1 ![]() for
for![]() ,
,![]() .
.
Proof. This is derived because ![]() by Equation (14) and
by Equation (14) and ![]() by Equation (16). [Q.E.D.]
by Equation (16). [Q.E.D.]
Theorem 3.2 ![]() for
for![]() ,
,![]() .
.
Proof. Referring to Equation (21), the indirect revenue induction coefficient is defined as![]() . Due to Equation (5) and Lemma 3.1, this theorem is derived. [Q.E.D.]
. Due to Equation (5) and Lemma 3.1, this theorem is derived. [Q.E.D.]
This theorem indicates that an increase in expenditure does not decrease revenue unless it causes a variation in the expenditure rate or the distribution rate of any others.
The lower limit of the indirect revenue induction coefficient is shown in Theorem 3.2, but its upper limit does not exist generally.17 However, regarding only the expenditure reflux coefficient, there is an upper limit. After proving some lemmas, we will clarify this upper limit.
Lemma 3.3 ![]() for
for![]() .
.
Proof. ![]() is the rth diagonal element of
is the rth diagonal element of![]() , and
, and ![]() is the
is the ![]() th non-diagonal
th non-diagonal
element of![]() . On the other hand,
. On the other hand, ![]() is the
is the ![]() th element of the inverse of
th element of the inverse of![]() .
.
Hence, by the definition of the inverse,
![]()
is satisfied for![]() . Summing up both sides of these formulas for
. Summing up both sides of these formulas for![]() , we obtain
, we obtain
![]() . (26)
. (26)
Note that,
![]()
Substituting this computation in Equation (26), we can see that ![]() for
for![]() . [Q.E.D.]
. [Q.E.D.]
Lemma 3.4 ![]() for
for![]() .
.
Proof. By ![]() (Equation (5)) and
(Equation (5)) and ![]() (Equation (14)),
(Equation (14)), ![]() is satisfied. Hence, we obtain
is satisfied. Hence, we obtain
![]() .
.
Considering this with ![]() (Equation (16)) and Lemma 3.3, we can derive
(Equation (16)) and Lemma 3.3, we can derive
![]() . (27)
. (27)
Moreover, the following equation holds by Equation (15).
![]() . (28)
. (28)
From Equations (27) and (28), we can see that ![]() for
for![]() . [Q.E.D.]
. [Q.E.D.]
Theorem 3.5 ![]() for
for![]() .
.
Proof. We confirmed ![]() in Lemma 3.4. If we multiply both sides of this formula by
in Lemma 3.4. If we multiply both sides of this formula by ![]() (Equation (5)), we obtain
(Equation (5)), we obtain ![]() for
for![]() . Considering Equation (21),
. Considering Equation (21), ![]() for
for ![]() is derived. [Q.E.D.]
is derived. [Q.E.D.]
This theorem indicates that one unit of expenditure does not reflux exceeding the expenditure rate of the first receiver unless it causes a variation in the expenditure rate or the distribution rate of any others.
We will qualitatively consider the reason that the expenditure reflux coefficient has an upper limit whereas the indirect revenue induction coefficient to the others does not have an upper limit generally. The revenue induction formula, which is derived from the partial equation, reflects money circulation of the inside of the others. Since money circulating unlimitedly is principally permitted, the indirect revenue induction coefficient to the others can be unlimitedly large. On the other hand, the formula does not reflect money circulation including the standard agent. That is, the flow of money reflected in the reflux coefficient is only from leaving to returning. As a result, money circulating unlimitedly cannot be expressed by the coefficient. Hence, the reflux coefficient is limited to a finite value.
Now, we have confirmed the upper limit of the reflux coefficient. Based on the above theorems, we can see the range of the reflux coefficient using concrete numbers.
Theorem 3.6 ![]() for
for![]() .
.
Proof. By Theorems 3.2 and 3.5, we obtain ![]() for
for![]() . Considering this with
. Considering this with ![]() (Equation (5)), we can see that
(Equation (5)), we can see that ![]() for
for![]() . [Q.E.D.]
. [Q.E.D.]
The reflux coefficient being equal to unity means that expenditure of an agent returns all to themselves. We decide that the situation ![]() is called the entire reflux of the standard agent through Agent h.
is called the entire reflux of the standard agent through Agent h.
Note that if the gross expenditure of the standard agent refluxes entirely, the expenditure reflux formula becomes
![]()
by Equations (15) and (24). In this case, the revenue for an agent is the sum of their own expenditure and all portions of the beginning money of the others.
Since the expenditure reflux is caused by the behaviors of the others, whether such a situation occurs or not also depends on them. We will derive an equivalent condition between the behaviors of the others and the entire reflux of the gross expenditure after proving some lemmas.
Lemma 3.7 If ![]() for
for![]() ,
, ![]() for
for![]() .
.
Proof. By the definition of the revenue induction coefficient (Equation (21)), ![]() is equivalent to
is equivalent to![]() . Note that
. Note that ![]() by Lemmas 3.1 and 3.4 and
by Lemmas 3.1 and 3.4 and ![]() by Equation (5). Therefore,
by Equation (5). Therefore, ![]() holds if and only if
holds if and only if ![]() and
and ![]() hold. Hence, if
hold. Hence, if ![]() for
for ![]() is premised,
is premised, ![]() for
for ![]() is derived. [Q.E.D.]
is derived. [Q.E.D.]
Lemma 3.8 If ![]() for
for![]() ,
, ![]() for
for![]() .
.
Proof. If we substitute ![]() for
for ![]() in the formula shown in Lemma 3.3, we obtain
in the formula shown in Lemma 3.3, we obtain ![]() for
for![]() . Transposing this equation, we can derive
. Transposing this equation, we can derive
![]() . (29)
. (29)
On the other hand, ![]() holds by Equation (15), thus we can see that
holds by Equation (15), thus we can see that
![]() . (30)
. (30)
From Equations (29) and (30), ![]() for
for ![]() is satisfied. Hence,
is satisfied. Hence, ![]() for
for ![]() is derived. If we substitute this in Equation (21) in the case
is derived. If we substitute this in Equation (21) in the case![]() , we obtain
, we obtain ![]() for
for![]() . Since
. Since ![]() for
for ![]() is premised,
is premised, ![]() for
for ![]() is derived. [Q.E.D.]
is derived. [Q.E.D.]
Theorem 3.9 ![]() for
for ![]() is equivalent to
is equivalent to ![]() for
for![]() .
.
Proof. Based on the definition of the expenditure rate (Equation (4)), ![]() for
for ![]() if and only if
if and only if ![]() for
for![]() . By Lemmas 3.7 and 3.8, this is equivalent to
. By Lemmas 3.7 and 3.8, this is equivalent to ![]() for
for![]() . [Q.E.D.]
. [Q.E.D.]
This theorem shows that the entire reflux of the gross expenditure occurs if and only if the end money of all others does not exist. It is intuitively reasonable.
If the end money of all others does not exist, any others do not possess money at term end even though their money does not disappear and is not transferred to the outside. In this case, to where does money go which the standard agent expends? The possibility is only that it goes to the standard agent. Hence, all portions of money which the agent expends must return to themselves. That is, all expenditure must reflux entirely.
Inversely, if some other agents retain their end money, a portion of money which the standard agent expends to the others should remain in the others’ hand. This means that all expenditure does not reflux entirely.
4. Concluding Comments
We have succeeded in deriving the revenue induction formula and the expenditure reflux formula. However, these formulas are not perfect as quantitative expressions of the revenue induction and the expenditure reflux.
If we directly use these formulas to examine an effect which a variation of expenditure has on revenue, we have to suppose that the indirect revenue induction coefficient is constant for a variation of expenditure. Since the coefficient is defined by the expenditure rate and the distribution rate of all others, the supposition also means that they are constant. But such a supposition does not seem to be justified generally. This restricts application ranges of those formulas.
However, even if the coefficient is variable, the effectiveness of the formulas derived in this paper is not completely lost. Even in such a case, the coefficient is still definable, and the propositions regarding its range clarified in this paper are also valid. We believe that our research is valuable as a primary approach to the truth of monetary economy.
NOTES
1“This class” refers to the productive expenditure class.
2Quesnay [1] pp.3-4 of “the ‘Third Edition’ of the Tableau Économique”.
3However, note that our revenue induction is directly a nominal phenomenon, not a real phenomenon. It is often said that the multiplier analysis was initially proposed by Richard Kahn (Cf. Kahn [2] ). However, although some opposing opinions exist, researchers have reported that there were predecessors of the multiplier analysis, including François Quesnay and Frederic Bastiat in France (Cf. Bortis [3] p. 63-64, Taylor [4] p. 7, 30-31, McGee [5] ), Karl Marx and Nicholas Johannsen and Alfred Schwoner in Germany (Cf. Trigg [6] p. 6-20, Sordi & Vercelli [7] , Hegeland [8] p. 5-14, 23-29, Schneider [9] p. 131-134, Klein [10] p. 143-147, Allsbrock [11] , Hagemann & Rühl [12] ), Julius Wulff and Frederik Johannsen and Jens Warming in Denmark (Cf. Hegeland [8] p. 14-19, Topp [13] , Dimand [14] p. 115-117, Boserup [15] , Warming [16] , Cain [17] , King [18] p. 68-69), Michał Kalecki in Poland (Cf. Sordi & Vercelli [7] p. 14-17, King [18] , Sawyer [19] ), Walter Bagehot and Arthur Cecil Pigou and Ralph Hawtrey in Britain (Cf. Hegeland [8] p. 3-5, 19-23, Dimand [14] p. 107-111, Heimann [20] p. 236-237, Wright [21] p. 185-186, Cain [22] , Dimand [23] , Darity & Young [24] , Ahiakpor [25] , Dimand [26] , Darity & Young [27] ), Alfred de Lissa and Lyndhurst Falkiner Giblin in Australia (Cf. Dimand [14] p. 105-107, 117-118, King [18] , Wright [21] p. 189-193, Ahiakpor [25] p. 896-897, Goodwin [28] , Arndt [29] , Markwell [30] p. 32-37, Millmow [31] , Coleman [32] ), and Charles Dow and John Maurice Clark in the United States (Cf. Heimann [20] p. 236-237, Bishop [33] , Fiorito [34] ).
4It is permitted that one element is either one agent or one group of agents, but we call it merely an agent.
5Cf. Miura [35] p. 190.
6Cf. Miura [35] p. 191.
7See the definition of the circular disposal in Miura [35] p. 189.
8Cf. Augustinovics [36] .
9In the case that we use regression analysis to verify the relationship between expenditure and revenue, a similar problem also occurs. Since the two flows are detected in a mixed state, regression analysis does not seem to be significant in the research examining the relationship between expenditure and revenue in money circulation.
10Cf. Miura [35] p. 191.
11![]() is an NPZ-matrix called in Miura [37] .
is an NPZ-matrix called in Miura [37] .
12Cf. Theorem 3.12 in Miura [37] . The prototype of this condition was first shown in Beauwens [38] and Neumann [39] .
13The space-time openness condition seems to be relevant to the bounded confidence condition in the literature of social opinion evolution. Cf. Varshney [40] , Shang [41] , Shang [42] regarding the bounded confidence condition.
14Cf. Theorem 3.5 in Miura [35] .
15Cf. Theorems 1.4 and 3.6 in Miura [37] .
16Cf. Miura [35] p. 191-192.
17This is obvious by the following concrete example. We suppose that the relevant society consists of two agents. In this case, the partial equation is![]() . From this,
. From this, ![]() If we differentiate
If we differentiate ![]() with respect to
with respect to![]() , we can derive
, we can derive![]() ,
,![]() . Considering
. Considering![]() , we can see that
, we can see that ![]() increases unlimitedly as
increases unlimitedly as ![]() approaches unity.
approaches unity.