1. Introduction
A vacation queueing system is one in which a server may become unavailable for a random period of time from a primary service center. The time away from the primary service center is called a vacation, and customers who arrive while the server is on vacation will have to wait until he returns from vacation. A vacation can be the result of many factors. In some cases, the vacation can be the result of server breakdown, which means that the system must be repaired and brought back to service. It can also be a deliberate action taken to utilize the server in a secondary service center when there are no customers present at the primary service center. Thus, server vacations are useful for those systems in which the server’s idle time is utilized for other purposes, and this makes the queueing model to be applicable to a variety of real world stochastic service systems.
One example of the application of vacation queueing systems is in token-passing local networks. In this case, a station can only transit its packets when it receives the token, which essentially corresponds to the server returning from a vacation. After transmitting the prescribed number of packets, the station passes the token to the next station in the transmitting order; this action is equivalent to the server taking a vacation with respect to that station. The station will transmit again when next it receives the token; or equivalently, when the server returns from vacation. In general, any system where service is provided in a round robin manner can be modeled by a vacation queueing system. Other applications that can be modeled by the vacation queueing system include machine breakdowns and maintenance in communication and computer systems. In these two cases, the server is unavailable to serve customers when the system breaks down or is intentionally taken out of service for maintenance. Thus, relative to the customers the server is on vacation.
There are different types of vacation queueing systems. In the single vacation scheme, the server takes a vacation of a random duration when the queue is empty. At the end of the vacation, the server returns to the queue. If there is at least one customer waiting when the server returns from vacation, the server performs one of the following actions depending on the service policy:
a) Under the exhaustive service policy, the server will serve all waiting customers as well as those that arrive while he is still serving at the station. He takes another vacation when the queue becomes empty.
b) Under the gated service policy, the server will serve only those customers that he finds at the queue upon his return from vacation. At the end of their service, the server will commence another vacation and any customers that arrive while the server is already serving at the station will be served when the server returns from the vacation.
c) Under the limited service policy, the server will serve only a predefined maximum number of customers and then will commence another vacation. The single-service scheme in which exactly one customer is served is a special type of this policy.
If the queue is empty on the server’s return, the server waits to complete a busy period using one of the above service policies before taking another vacation.
In the multiple vacation scheme, if the server returns from a vacation and finds the queue empty, he immediately commences another vacation. If there is at least one waiting customer, then he will commence service according to the prevailing service policy.
Queueing systems with server vacations have attracted the attention of many researchers since the idea was first discussed in the paper of Levy and Yechiali [1] . Several excellent surveys on these vacation models have been done by Doshi [2] [3] , and the books by Takagi [4] and Tian and Zhang [5] are devoted to the subject. One of the most remarkable results for vacation queueing systems is the stochastic decomposition result, which is introduced by Fuhrmann and Cooper [6] and allows the system’s behavior to be analyzed by considering separately the distribution of system (queue) size with no vacation and additional system size due to vacation.
Many new vacation queueing systems have been proposed. In the vacation queueing system, we have described the server completely stops service or is switched off when he is on vacation. Recently, Servi and Finn [7] introduced the working vacation scheme, in which the server worked at a different rate rather than completely stopping service during a vacation. The working vacation scheme has attracted a lot of research effort, and several authors have extended the original model. Wu and Takagi [8] generalized the model in [7] to an M/G/1 queue with general working vacations. Baba [9] studied a GI/M/1 queue with working vacations by using the matrix analytic method. Banik, Gupta and Pathak [10] analyzed the GI/ M/1/N queue with working vacations. Liu, Xu and Tian [11] established a stochastic decomposition result in the M/M/1 queue with working vacations. In [12] , Krishnamoorthy and Sreenivasan considered an M/M/2 queueing system with heterogeneous servers where one server is always available and the other goes on a working vacation when there are no customers in the system.
The differentiated multiple vacation queueing system is another vacation queueing model that is proposed by Ibe and Isijola [13] . The authors considered an M/M/1 multiple vacation queueing system with two types of vacations: Type 1 vacation is taken when the server returns from a vacation and finds at least one waiting customer; it takes the vacation after exhaustively serving all customers in the system. Type 2 vacation is taken when the server returns from a vacation and finds no customers in waiting to be served. The duration of one type of vacation is different from that of the other type.
Another model of the vacation queueing system is the system with vacation interruption in which the server can come back to the normal working level before the vacation ends. Li and Tian [14] analyzed an M/M/1 queue with working vacations and vacation interruption. The authors also extended the model to the GI/Geo/1 queue with working vacation and vacation interruptions [15] . The GI/M/1 queue with working vacations and vacation interruption was studied by Li, Tian and Ma [16] . Similarly, Zhang and Hou [17] discussed an M/G/1 queue with multiple working vacations and vacation interruption. In [18] , Sreenivasan, Chakravarthy and Krishnamoorthy considered a single server queueing model in which customers arrived according to a Markovian arrival process. They also introduces a threshold, N, where , such that the server offering services (at a lower rate) during a vacation will have the vacation interrupted the moment the queue size reaches N. In [19] Isijola-Adakeja and Ibe extended the model on [13] to include server vacation interruption.
, such that the server offering services (at a lower rate) during a vacation will have the vacation interrupted the moment the queue size reaches N. In [19] Isijola-Adakeja and Ibe extended the model on [13] to include server vacation interruption.
In the vacation models that have been analyzed in the literature, server timeouts have not been considered. In this paper, we consider vacation queueing systems with server timeouts. Specifically, we consider a system that operates in the following manner. When the server has finished serving a customer and finds the system empty, it takes a vacation whose duration is independent of both the service time and the inter-arrival time. At the end of the vacation, the server returns to serve those customers, if any, who arrive during its vacation. It will commence another vacation when the system becomes empty. If no customer arrives during the vacation, the server waits for a fixed time c. If no customer arrives by the end of this period, the server commences another vacation. If a customer arrives before the period expires, the server commences service and serves exhaustively before commencing another vacation.
The paper is organized as follows. The model is formally defined in Section 2 and analyzed in Section 3. An extension of the model to the N-policy scheme is given in Section 4, and concluding remarks are made in Section 5.
2. Model Description
Figure 1 illustrates this scheme. Assume that the system has been operational for some time and the server returns from a vacation of duration V1 at a time labeled t1 and found two customers C1 and C2 waiting. Before completing the service of these customers, another customer C3 arrives. After serving the three customers the server takes another vacation of duration V2. Upon returning from that vacation at a time t2 it found no customer waiting. It waits for a time of duration c without any customer arriving. It thus leaves for another vacation of duration V3 without serving a customer. It came back from the vacation at the time labeled t3 and found two customers C4 and C5 waiting. Before completing the service of these customers, another customer C6 arrives. After serving these three customers, the server takes another vacation of duration V4. Upon returning from the vacation at the time labeled t4, it found no waiting customers. However, before the expiration of the timeout, customer C7 arrives to initiate another busy period, and the process continues.
This vacation queueing is essentially a hybrid multiple and single vacation scheme that was introduced in Ibe and Trivedi [20] . The main objective of the model in [20] was to demonstrate how vacation queueing systems with exponentially distributed service times and finite population could be modeled by the stochastic Petri net. In this paper we assume that the population is infinite and service times have arbitrary distribution.
One important application of the vacation scheme with server timeout is to enhance resource utilization in the single vacation model. Specifically, if there is a problem in the arrival process that prevents customers from arriving for service, the server may be idle indefinitely after returning from a vacation in the single vacation. But when the idle time is bounded as described above, the server can be used to perform other functions at the
![]()
Figure 1. Vacation queueing scheme with timeout.
expiration of the timeout rather than wait indefinitely. Thus, when the source is subject to breakdown, such as the disruption of the communication links along which messages arrive in a communication system, the server timeout scheme prevents the server from waiting indefinitely for customers to arrive after returning from a vacation.
Two other hybrid vacation schemes have been proposed. In Kella [21] , if the server returns from the 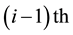 vacation and finds the system empty, it takes another vacation with probability
vacation and finds the system empty, it takes another vacation with probability 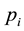 and waits for the first customer to arrive with probability
and waits for the first customer to arrive with probability . In the later case the server takes a vacation after serving exhaustively. In [4] if the server returns from a vacation and finds the system empty, it takes at most J vacations repeatedly until it finds at least one customer waiting in the system when it returns from a vacation. If no customer arrives by the Jth vacation, the server waits until a customer arrives.
. In the later case the server takes a vacation after serving exhaustively. In [4] if the server returns from a vacation and finds the system empty, it takes at most J vacations repeatedly until it finds at least one customer waiting in the system when it returns from a vacation. If no customer arrives by the Jth vacation, the server waits until a customer arrives.
3. Analysis of the Model
We assume that customers arrive at the system according to a Poisson process with rate . The time, X, to serve a customer has a general distribution with cumulative distribution function (CDF)
. The time, X, to serve a customer has a general distribution with cumulative distribution function (CDF) , mean
, mean 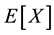 and second moment
and second moment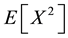 . The s-transform of the probability density function (PDF) of X,
. The s-transform of the probability density function (PDF) of X, 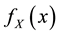 , is
, is , which is defined by (see, for example, [22] ):
, which is defined by (see, for example, [22] ):

where 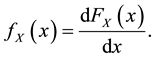
The duration, V, of a vacation is also assumed to have a general distribution with CDF 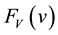 and s-transform
and s-transform![]() . The mean of V is
. The mean of V is ![]() and its second moment is
and its second moment is![]() . X and V are mutually independent. Let the random variable A denote the number of customers in the system at the beginning of a busy period. The probability mass function (PMF) of A is
. X and V are mutually independent. Let the random variable A denote the number of customers in the system at the beginning of a busy period. The probability mass function (PMF) of A is ![]() whose z-transform,
whose z-transform, ![]() , is given by
, is given by
![]()
The mean of A is ![]() and its second moment is
and its second moment is![]() . Let the random variable B denote the number of customers left behind by an arbitrary departing customer, and let L denote the number of customers in the system at an arbitrary point in time. The PMF of B is
. Let the random variable B denote the number of customers left behind by an arbitrary departing customer, and let L denote the number of customers in the system at an arbitrary point in time. The PMF of B is ![]() whose z-transform is given by
whose z-transform is given by![]() . The mean of B is
. The mean of B is ![]() and its second moment is
and its second moment is![]() . Similarly, the PMF of L is
. Similarly, the PMF of L is ![]() whose z-transform is given by
whose z-transform is given by![]() . The mean of L is
. The mean of L is ![]() and its second moment is
and its second moment is![]() . Let
. Let ![]() denote the waiting time in the system, and let the utilization factor be defined by
denote the waiting time in the system, and let the utilization factor be defined by![]() . The main result of the analysis is the following:
. The main result of the analysis is the following:
Theorem 1: The mean waiting time in the system is given by
![]()
The proof of this theorem is given in the Appendix 1.
We consider the limiting cases for c:
![]()
![]()
These are the results obtained in [1] for the multiple vacation queueing system and the single vacation queue-
ing system, respectively. Note that ![]() monotonically decreases as c increases since
monotonically decreases as c increases since
![]()
which is consistent with the fact that the single vacation scheme ![]() has a smaller mean waiting time than the multiple vacation scheme
has a smaller mean waiting time than the multiple vacation scheme![]() . Also, in [4] it is shown that the s-transform of the PDF of the waiting time is given by
. Also, in [4] it is shown that the s-transform of the PDF of the waiting time is given by
![]()
As shown in the Appendix,
![]()
where
![]()
Applying this result to our model yields
![]()
which, on differentiation and evaluating at![]() , gives the same value of
, gives the same value of ![]() obtained earlier.
obtained earlier.
Although the model has been analyzed with fixed timeout c, the analysis can be extended to the case where the timeout is a random variable T with mean ![]() and the s-transform of the PDF of T is
and the s-transform of the PDF of T is![]() . In this case only a slight modification is required in the results. Specifically, we replace the factor
. In this case only a slight modification is required in the results. Specifically, we replace the factor ![]() with
with![]() .
.
Numerical Results
We assume that X is exponentially distributed with mean![]() . Also, if we define the PDF of X by
. Also, if we define the PDF of X by![]() ,
, ![]() , then
, then ![]() and
and![]() . Similarly, we assume that V has an exponential distribution with a mean of 5. This means that
. Similarly, we assume that V has an exponential distribution with a mean of 5. This means that![]() ,
,![]() ;
;![]() ;
; ![]() and
and
![]()
Thus we have that
![]()
Table 1 shows the values of ![]() for different values of c.
for different values of c.
From the table we observe that at low values of ![]() (i.e., low offered load), the mean delay decreases as c increases. However, at high values of offered load, the mean delay becomes almost identical for all values of c. The reason for this is because at high values of offered load the server is likely to be serving customers more than he takes vacations.
(i.e., low offered load), the mean delay decreases as c increases. However, at high values of offered load, the mean delay becomes almost identical for all values of c. The reason for this is because at high values of offered load the server is likely to be serving customers more than he takes vacations.
![]()
Table 1. Values of ![]() for different values of c.
for different values of c.
4. The N-Policy with Timeout
The N-policy was introduced by Yadin and Naor [23] and operates as follows. The server goes on vacation at the end of a busy period. The vacation ends with the arrival of the Nth customer since the end of the last busy period.
The N-policy scheme with timeout operates as follows. Consider cycles of busy periods and let ![]() denote the arrival time of the ith customer in the lth cycle, where
denote the arrival time of the ith customer in the lth cycle, where ![]() and
and ![]() Starting from the arrival of the first customer in a given cycle, if less than
Starting from the arrival of the first customer in a given cycle, if less than ![]() other customers arrive within the time interval c, then the server’s vacation ends and service is performed exhaustively at the end which another vacation begins. Assume that the system is empty and, therefore, the server is on the lth vacation. The vacation ends at time
other customers arrive within the time interval c, then the server’s vacation ends and service is performed exhaustively at the end which another vacation begins. Assume that the system is empty and, therefore, the server is on the lth vacation. The vacation ends at time ![]() given by
given by
![]()
That is, the vacation ends at time ![]() (when the Nth customer arrives) or (if less than
(when the Nth customer arrives) or (if less than ![]() other customers arrive within the timeout period c measured from when the first customer arrived), whichever comes first. This means that each busy period begins with either N customers, if
other customers arrive within the timeout period c measured from when the first customer arrived), whichever comes first. This means that each busy period begins with either N customers, if![]() , or n customers,
, or n customers, ![]() , otherwise. The server serves exhaustively and takes another vacation when the system becomes empty, whatever number of customers the busy period begins with.
, otherwise. The server serves exhaustively and takes another vacation when the system becomes empty, whatever number of customers the busy period begins with.
The scheme is illustrated in Figure 2, where it is assumed that![]() . In the figure, during the server’s first server vacation customer
. In the figure, during the server’s first server vacation customer ![]() arrives and thus activates the timer. By the time the timeout expired only one other customer,
arrives and thus activates the timer. By the time the timeout expired only one other customer, ![]() , arrived. Since the timeout has expired with less than 3 customers in the system, the server initiates a busy period with two customers at time
, arrived. Since the timeout has expired with less than 3 customers in the system, the server initiates a busy period with two customers at time![]() . Another customer,
. Another customer, ![]() , arrived during this busy period. After serving all 3 customers, the server takes a vacation. While the server is on vacation, customer
, arrived during this busy period. After serving all 3 customers, the server takes a vacation. While the server is on vacation, customer ![]() arrives to activate the timer for the next cycle. The time expires at time
arrives to activate the timer for the next cycle. The time expires at time ![]() and the server initiates a busy period at that time with only one customer. During this busy period, customers
and the server initiates a busy period at that time with only one customer. During this busy period, customers ![]() and
and ![]() arrive and are served before the server commences another vacation. While the server is on vacation, customer
arrive and are served before the server commences another vacation. While the server is on vacation, customer ![]() arrives and activates the time. Before the timer expires customer
arrives and activates the time. Before the timer expires customer ![]() arrives. The timer expires at time
arrives. The timer expires at time ![]() and the server initiates a busy period at that time with two customers. During that busy period customer
and the server initiates a busy period at that time with two customers. During that busy period customer ![]() arrives and is served before the server commences another vacation. The process continues, as shown in the figure. The intervals labeled
arrives and is served before the server commences another vacation. The process continues, as shown in the figure. The intervals labeled![]() ,
, ![]() , indicate the vacation intervals under the normal N-policy.
, indicate the vacation intervals under the normal N-policy.
The analysis of the model is similar to that for the single vacation with server timeout and the mean waiting time in the system is given by the following theorem:
Theorem 2: The mean waiting time in the system is given by
![]()
The proof of the theorem is given in Appendix 2 where it is also shown that
![]()
![]()
which are the results for a standard M/G/1 queue with no server vacation and a standard N-policy scheme without timeout, as shown in [23] , respectively. Also, we observe that
![]()
which means that the expected waiting time monotonically increases with c. Therefore, the optimal value of c is zero.
Numerical Results
We use the same parameters as in Section 3.1 and assume that![]() . Then we have that
. Then we have that
![]()
Table 2 shows the values of ![]() for different values of c.
for different values of c.
Observe that when ![]() the minimum value of
the minimum value of ![]() occurs around
occurs around![]() . This can easily be verified for the case of
. This can easily be verified for the case of ![]() by observing that
by observing that
![]()
Differentiating this function with respect to ![]() and setting the result to zero gives the optimal value at
and setting the result to zero gives the optimal value at![]() . Since the second derivative is greater than zero, we conclude that
. Since the second derivative is greater than zero, we conclude that ![]() gives the minimum mean delay. We can also rewrite the expression for
gives the minimum mean delay. We can also rewrite the expression for ![]() as follows:
as follows:
![]()
![]()
Table 2. Values of ![]() for different values of c at
for different values of c at![]() .
.
Thus, the factor ![]() has a damping effect on the mean delay at
has a damping effect on the mean delay at![]() . This means that as c increases, the mean delay tends to slightly increase, which agrees with the statement we made earlier that the optimal value of c is zero.
. This means that as c increases, the mean delay tends to slightly increase, which agrees with the statement we made earlier that the optimal value of c is zero.
Observe also that at low offered load, the value of the expected delay when ![]() is almost equal to the value at high offered load. This is due to the delay encountered by customers by waiting for the timeout to expire before they can be served.
is almost equal to the value at high offered load. This is due to the delay encountered by customers by waiting for the timeout to expire before they can be served.
5. Conclusions
We have derived expressions for the mean waiting time of a vacation queueing system in which the server does not immediately take another vacation upon returning from a vacation and finding the system empty, as in the multiple vacation scheme, or wait indefinitely for a customer to arrive, as in the single vacation scheme. In the proposed model, if the server returns from a vacation and finds the system empty, it waits for a fixed time c. If at the expiration of this time, no customer arrives, the server will take a vacation; otherwise it servers arriving customers exhaustively before taking another vacation. The results of the analysis are consistent with those of the multiple vacations scheme (where![]() ), and the single vacation scheme (where
), and the single vacation scheme (where![]() ). Numerical results are also given that show the impact of the timeout period on the mean delay. A linear cost model was assumed to obtain the optimal value of for the assumed model. Numerical results are obtained under a set of parameter assumptions, and the results indicate that there is a very small range of values of the offered where meaning optimization can be applied.
). Numerical results are also given that show the impact of the timeout period on the mean delay. A linear cost model was assumed to obtain the optimal value of for the assumed model. Numerical results are obtained under a set of parameter assumptions, and the results indicate that there is a very small range of values of the offered where meaning optimization can be applied.
The model is also extended to the N-policy scheme where the timeout is measured from the arrival of the first customer since the end of the last busy period. The results have also been shown to be consistent with earlier results for the case when![]() , which is the standard M/G/1 queue, and the case when
, which is the standard M/G/1 queue, and the case when![]() , which is the N-policy scheme without timeout. It is shown that the expected waiting time increases monotonically with c, which means that
, which is the N-policy scheme without timeout. It is shown that the expected waiting time increases monotonically with c, which means that ![]() gives the minimum expected waiting time. Numerical results are also obtained that show that the mean delay has a minimum value around
gives the minimum expected waiting time. Numerical results are also obtained that show that the mean delay has a minimum value around![]() .
.
Appendix 1
In this section we provide a formal proof of theorem proposed in Section 3. Let ![]() denote the z-transform of the PMF of the number of customers in the system is a standard M/G/1 queue (i.e., one in which the server never takes a vacation). As defined earlier, let
denote the z-transform of the PMF of the number of customers in the system is a standard M/G/1 queue (i.e., one in which the server never takes a vacation). As defined earlier, let ![]() denote the z-transform of the number of customers in the system at an arbitrary point in time and let
denote the z-transform of the number of customers in the system at an arbitrary point in time and let ![]() denote the z-transform of the PMF of the number of customers left behind by an arbitrary departing customer. From the stochastic decomposition result we have that
denote the z-transform of the PMF of the number of customers left behind by an arbitrary departing customer. From the stochastic decomposition result we have that
![]()
It is well known (see Kleinrock [24] , for example) that
![]()
Let T denote the total time that a customer spends in the system. Thus, applying Little’s law [25] we obtain the mean waiting time as
![]()
Thus, once ![]() is known, we can obtain
is known, we can obtain![]() . The remainder of the proof is devoted to deriving the expressions for
. The remainder of the proof is devoted to deriving the expressions for ![]() and
and![]() , the s-transform of the PDF of the waiting time.
, the s-transform of the PDF of the waiting time.
Consider the following mutually exclusive events associated with the server’s experience after returning from a vacation:
1) The server returns from vacation, waits and commences another vacation without serving a customer; the probability of this event is![]() .
.
2) The server returns from vacation, waits and serves at least one customer before taking another vacation; the probability of this event is![]() .
.
3) The server returns from vacation and finds at least one waiting customer; the probability of this event is![]() .
.
Under event 2, a busy period is initiated with exactly one customer in the system. Similarly, under event 3, a busy period is initiated with at least one customer in the system. Therefore, if we define ![]() as the probability of event k, given that a busy period was initiated before the server commences another vacation, where
as the probability of event k, given that a busy period was initiated before the server commences another vacation, where![]() , then we obtain the following result:
, then we obtain the following result:
![]()
where
![]()
From this we obtain the result
![]()
![]()
![]()
which completes the proof.
Appendix 2
In this appendix we prove Theorem 2 that was proposed in Section 4. For the current scheme, a busy period will commence with exactly N customers in the system with probability![]() , which is the probability of
, which is the probability of ![]() or more Poisson arrivals in an interval of length c and thus is given by
or more Poisson arrivals in an interval of length c and thus is given by
![]()
Similarly, a busy period will commence with n customers, ![]() , with probability
, with probability![]() , which is the probability of exactly
, which is the probability of exactly ![]() Poisson arrivals in an interval of length c and is given by
Poisson arrivals in an interval of length c and is given by
![]()
Therefore,
![]()
If we define D as the event that there are N customers at the beginning of a busy period and E as the event that there are less than N customers at the beginning of a busy period, then mimicking the method used in Takagi [4] we obtain the following conditional s-transforms of the PDF of the waiting time:
![]()
Thus, the unconditional s-transform of the PDF of the waiting time is given by
![]()
From this we obtain the mean waiting time as
![]()
Before considering the limiting values of c, recall that the expected value of A is given by
![]()
Thus, ![]() and
and![]() . This implies that
. This implies that
![]()
which are the results for a standard M/G/1 queue with no server vacation and a standard N-policy scheme without timeout, as shown in [23] , respectively. This completes the proof.