A Special Case on the Stability and Accuracy for the 1D Heat Equation Using 3-Level and θ-Schemes ()
1. Introduction
In this paper we have considered the heat equation 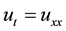 with
with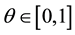 . Using
. Using 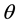 -scheme and 3-level scheme in space we compute the order of local accuracy in space and time and stability restriction as a function of
-scheme and 3-level scheme in space we compute the order of local accuracy in space and time and stability restriction as a function of 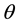 on the time step
on the time step . Much attention has been paid to the development, analysis and implementation of accurate methods for the numerical solution of this problem in the literature. Many problems are modeled by smooth initial conditions and Dirichlet boundary conditions. A number of procedures have been suggested (see, for instance [1] - [3] ). We can say that three classes of solution techniques have emerged for solution of PDE: the finite difference techniques, the finite element methods and the spectral techniques (see [4] and [5] ). The last one has the advantage of high accuracy attained by the resulting discretization for a given number of nodes [6] - [8] .
. Much attention has been paid to the development, analysis and implementation of accurate methods for the numerical solution of this problem in the literature. Many problems are modeled by smooth initial conditions and Dirichlet boundary conditions. A number of procedures have been suggested (see, for instance [1] - [3] ). We can say that three classes of solution techniques have emerged for solution of PDE: the finite difference techniques, the finite element methods and the spectral techniques (see [4] and [5] ). The last one has the advantage of high accuracy attained by the resulting discretization for a given number of nodes [6] - [8] .
We consider Scheme (1) for the 1D heat equation for some parameter . We compute the order of local accuracy in space and time as a function of
. We compute the order of local accuracy in space and time as a function of 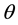 and its the stability restriction. Until
and its the stability restriction. Until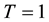 , we compute the solution with some fixed
, we compute the solution with some fixed 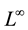 error with the smallest amount of CPU time, and finally we can see this findings producing the relevant convergence and efficiency plot. For the 3-level scheme we consider (11) for the 1D heat equation and we compute the local truncation error. For different values of
error with the smallest amount of CPU time, and finally we can see this findings producing the relevant convergence and efficiency plot. For the 3-level scheme we consider (11) for the 1D heat equation and we compute the local truncation error. For different values of 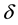 and
and 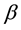 we find the stability criterion of the scheme and its accuracy.
we find the stability criterion of the scheme and its accuracy.
2.  -Scheme
-Scheme
Let
 (1)
(1)
be the ![]() -scheme applied to the one-dimensional heat equation
-scheme applied to the one-dimensional heat equation
![]() (2)
(2)
Now for the order of local accuracy in space and time as a function of ![]() we write the local truncation error. In time we have
we write the local truncation error. In time we have
![]()
where ![]() represents the exact solution of the heat equation. Now we perform Taylor expansion of
represents the exact solution of the heat equation. Now we perform Taylor expansion of ![]() at
at![]() .
.
![]()
We can write the LHS of (1) as
![]() (3)
(3)
![]() (4)
(4)
here ![]() represents the derivative with respect to time, of
represents the derivative with respect to time, of![]() . On the RHS, we have a centered difference approximating second derivative of
. On the RHS, we have a centered difference approximating second derivative of ![]()
![]() (5)
(5)
As we are solving the heat equation, the previous expression is
![]() (6)
(6)
Now, at time ![]() we have
we have
![]() (7)
(7)
![]() (8)
(8)
therefore, applying Taylor expansion with respect to ![]() we can write
we can write
![]()
![]()
![]()
So (8) becomes
![]() (9)
(9)
Here RHS of (1) becomes
![]()
After the elimination of some terms we have
![]()
Now simplifying we obtain
![]()
Cancelling ![]() and moving all terms to the right side, we get
and moving all terms to the right side, we get
![]() (10)
(10)
Scheme (10) is first order in time, second order in space. If for example![]() , it becomes second order, this is due to cancellation of the
, it becomes second order, this is due to cancellation of the![]() .
.
Stability Restriction as a Function of ![]()
Here we will apply Von Neumann stability. Let ![]() and
and![]() . Then Equation (1) can be written as
. Then Equation (1) can be written as
![]()
Now dividing by ![]() we have
we have
![]()
![]()
Therefore by using ![]() and
and ![]() we can rewrite the expression as
we can rewrite the expression as
![]()
![]()
![]()
![]()
![]()
By using the identity ![]() we have
we have
![]()
We can say this scheme is stable only for![]() . Now, let
. Now, let![]() . The inequality is
. The inequality is
![]()
thus
![]()
Now multiplying by the denominator we have
![]()
![]()
The expression in the absolute value becomes
![]()
Therefore by the Von Neumann stability condition, the scheme is stable if![]() .
.
In this case we can say the following about the best combination for ![]() and
and![]() . In order to have both local accuracy and stability, the optimal value of
. In order to have both local accuracy and stability, the optimal value of ![]() is
is ![]() and therefore this scheme represents the Crank-Ni- cholson scheme. Here
and therefore this scheme represents the Crank-Ni- cholson scheme. Here ![]() and
and ![]() appear in the form
appear in the form![]() .
.
In Figure 1 the convergence plot equation (varying the radio r) is
![]()
with matrix A described in the heat equation. We can say the scheme is unconditionally stable. We can see in Figure 1 that we have a linear convergence with respect to r.
3. Three-Level Scheme
We start by computing the stability restriction one has to impose on![]() . We apply Von Neumannstability analysis to the scheme.
. We apply Von Neumannstability analysis to the scheme.
Let
![]() (11)
(11)
where
![]() (12)
(12)
and
![]() (13)
(13)
By using (12) and (13) we can rewrite (11) as
![]() (14)
(14)
or as
![]()
The local truncation error for this scheme ![]() is as follow.
is as follow.
![]()
where ![]() represents the exact solution of the heat equation. Therefore we have
represents the exact solution of the heat equation. Therefore we have
![]() (15)
(15)
Now expanding ![]() operator on the left side, we can isolate the forward difference in time at
operator on the left side, we can isolate the forward difference in time at![]() , then
, then
![]()
however,
![]()
Expanded this expression becomes
![]()
Finally we have
![]()
4. Stability Criterion for the Three-Level Scheme and Its Accuracy When ![]() and
and ![]()
By using Equation (14) we have
![]()
Now applying Von Neumann stability again, the aim is to use ![]() and
and ![]() , therefore
, therefore
![]()
Multiplying both sides by ![]() and write
and write ![]() we obtained
we obtained
![]()
Using the cosine identity that ![]() we have
we have
![]()
We have a quadratic equation in![]() , where
, where![]() , therefore
, therefore
![]()
After some cancellations, we can write
![]()
Here, if all ![]() we need
we need
![]()
![]()
Acknowledgements
We would like to thank the referee for his valuable suggestions that improved the presentation of this paper.