1. Introduction
In 1963, R. P. Kerr [1] proposed a metric that describes a massive rotating object. Since then, a huge amount of papers about the structure and astrophysical applications of this spacetime appeared. Now, it is widely believed that this metric does not represent the spacetime of a rotating astrophysical object. In 1967, Hernández [2] stated that reasonable perfect fluid type solutions which might serve as source of the Kerr metric may not exist. In 1971, Thorne [3] [4] added that because of the relationship between multipole moments and angular momentum, the Kerr solution cannot represent correctly the external field of any realistic stars. Moreover, the Kerr metric has difficulties when matching it to a realistic interior metric according to [5] . However, there has been a con- siderable amount of efforts trying to match the Kerr metric with a realistic interior metric that represents a physical source, see for example [6] - [12] . For a concise and comprehensive review of the different methods that have been used in order to try and obtain an interior solution for the Kerr metric, see [13] .
In [14] and [15] , the Newman-Janis algorithm was applied to look for interior solutions. Drake and Turolla [14] also propose a general method for finding interior solutions with oblate spheroidal boundary surfaces and note that the boundary surfaces reduce to a sphere in the case with no rotation, however Vaggiu in [15] argues that it is more helpful to start with the Schwarzschild interior and then proceed to the Kerr interior. Vaggiu uses an anisotropic conformally flat static interior and is led to interior Kerr solutions with oblate spheroidal boun- dary surfaces, additionally he points out that his procedure can be applied to find interior solutions matching with a general asymptotically flat vacuum stationary spacetime.
Other exact rotating solutions to the Einstein field equations (EFE) containing mass multipoles and magnetic dipole were obtained by [16] - [23] . In the first four articles, they used the Ernst formalism [24] , while in the four last ones, the solutions were obtained with the help of the Hoenselaers-Kinnersley-Xanthopoulos (HKX) trans- formations [25] . These authors obtain new metrics from a given seed metric. These formalisms allow to include other desirable characteristics (rotation, multipole moments, magnetic dipole, etc.) to a given seed metrics. Furthermore, Quevedo in [26] not only presents an exact electrovacuum solution that can be used to describe the exterior gravitational field of a rotating charged mass distribution, but also considers the matching using the derivatives of the curvature eigenvalues, this leads to matching conditions from which one can expect to obtain the minimum radius at which the matching can be made.
In Nature, it is expected that astrophysical objects are rotating and slightly deformed as is pointed out in [27] and in [28] . In addition, Andersson and Comer in [27] use a two-fluid model for a neutron star, one layer with neutrons that has a differential rotation and another layer consisting of a solid crust with constant rotation. The aim of this article is to derive an appropriate analytical tractable metric for calculations in which the quadrupole moment can be treated as a perturbation, but for arbitrary angular momentum. Moreover, this metric should be useful to tackle astrophysical problems, for instance, accretion disk in compact stellar objects [27] - [30] , re- lativistic magnetohydrodynamic jet formation [31] , astrometry [32] [33] and gravitational lensing [34] . Further- more, software related with applications of the Kerr metric can be easily modified in order to include the quad- rupole moment [35] - [37] .
This paper is organized as follows. In Section 2, we give a succinct explanation of the Kerr metric, and the weak limit of the Erez-Rosen metric is presented. In Section 3, the Lewis metric is presented, and the pertur- bation method is discussed. The application of this method leads to a new solution to the EFE with quadrupole moment and rotation. It is checked by means of the REDUCE software [38] that the resulting metric is a solu- tion of the EFE. In section 4, we compare our solution with the exterior Hartle-Thorne metric in order to assure that our metric has astrophysical meaning. Forthcoming works with this metric are discussed in Section 6.
2. The Kerr Metric and the Erez-Rosen Metric
2.1. The Kerr Metric
The Kerr metric represents the spacetime of a non-deformed massive rotating object. The Kerr metric is given by [1] [39]
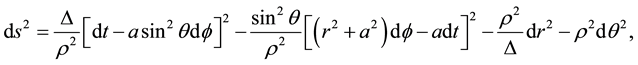 (1)
(1)
where 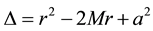 and
and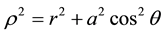 . M and a represent the mass and the rotation parameter, respectively. The angular momentum of the object is
. M and a represent the mass and the rotation parameter, respectively. The angular momentum of the object is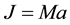 .
.
2.2. The Erez-Rosen Metric
The Erez-Rosen metric [39] - [42] represents the spacetime of a body with quadrupole moment. The principal axis of the quadrupole moment is chosen along the spin axis, so that gravitational radiation can be ignored. Here, we write down an approximate expression for this metric obtained by doing Taylor series [32]
 (2)
(2)
where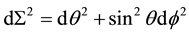 , and
, and
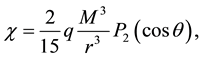 (3)
(3)
where . The quadrupole parameter is given by
. The quadrupole parameter is given by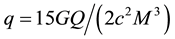 , with Q representing the quadrupole moment. This metric is valid up to the order
, with Q representing the quadrupole moment. This metric is valid up to the order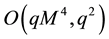 .
.
3. Perturbing the Kerr Metric
3.1. The Lewis Metrics
The Lewis metric is given by [39] [43]
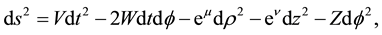 (4)
(4)
where we have chosen the canonical coordinates  and
and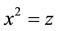 , V, W, Z, m and n are functions of r and z
, V, W, Z, m and n are functions of r and z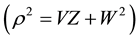 . Choosing
. Choosing 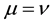 and performing the following changes of potentials
and performing the following changes of potentials
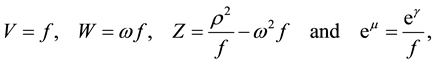
we get the Papapetrou metric
![]() (5)
(5)
3.2. The Perturbation Method
In order to include a small quadrupole moment into the Kerr metric we will modify the Lewis-Papapetrou metric (5). First of all, we choose expressions for the canonical coordinates r and z. For the Kerr metric [1] , one particular choice is [39] [44]
![]() (6)
(6)
where![]() .
.
From (6) we get
![]() (7)
(7)
If we choose
![]()
the term (7) becomes
![]()
where![]() .
.
From (5), we propose the following metric
![]() (8)
(8)
where
![]() (9)
(9)
where the potentials![]() , and
, and ![]() depend on
depend on ![]() and
and![]() . The potential
. The potential ![]() is then chosen to maintain the same cross components of the Kerr metric.
is then chosen to maintain the same cross components of the Kerr metric.
Now, let us choose
![]() (10)
(10)
The only potential we have to find is![]() . In order to obtain this potential, the EFE must be solved
. In order to obtain this potential, the EFE must be solved
![]() (11)
(11)
where ![]() are the Ricci tensor components and R is the curvature scalar. The Ricci tensor components and the curvature scalar R for this metric can be found in the Appendix.
are the Ricci tensor components and R is the curvature scalar. The Ricci tensor components and the curvature scalar R for this metric can be found in the Appendix.
In our calculations, we consider the potential ![]() as perturbation, i.e. one neglects terms of the form
as perturbation, i.e. one neglects terms of the form
![]()
Terms containing factors of the form
![]()
are also neglected. Substituting the known potentials ![]() into the expressions for the Ricci tensor and the curvature scalar (see Appendix) results only in one equation for
into the expressions for the Ricci tensor and the curvature scalar (see Appendix) results only in one equation for ![]() that we have to solve:
that we have to solve:
![]() (12)
(12)
The solution for this equation is
![]() (13)
(13)
where ![]() is a constant. To determine this constant, we compare the weak limit of the metric (8) with the approximate Erez-Rosen metric (2). The result is
is a constant. To determine this constant, we compare the weak limit of the metric (8) with the approximate Erez-Rosen metric (2). The result is ![]()
![]() .
.
Then, the new modified Kerr metric containing quadrupole moment is
![]() (14)
(14)
where the tilde over ![]() is now dropped.
is now dropped.
We verified that the metric (14) is indeed a solution of the EFE using REDUCE [38] up to the order![]() .
.
Note that (14) has four important limiting cases. One obtains the Kerr metric (1) if![]() , the weak metric of [32] if
, the weak metric of [32] if![]() , the Erez-Rosen-like metric (2) if
, the Erez-Rosen-like metric (2) if![]() , and the Schwarzchild metric if
, and the Schwarzchild metric if![]() .
.
4. Comparison with the Exterior Hartle-Thorne Metric
In order to validate the metric (14) as representing the gravitational field of a real astrophysical object, one should show that it is possible to construct an interior solution, which can appropriately be matched with our exterior solution. To this aim, we employed the exterior Hartle-Thorne metric [5] [32] [45] [46]
![]() (15)
(15)
where![]() ,
, ![]() , and
, and ![]() are related with the total mass, angular momentum, and mass quadrupole moment of the rotating object, respectively. This approximation for the Hartle-Thorne metric (15) was obtained by Frutos- Alfaro et al. using a REDUCE program [32] .
are related with the total mass, angular momentum, and mass quadrupole moment of the rotating object, respectively. This approximation for the Hartle-Thorne metric (15) was obtained by Frutos- Alfaro et al. using a REDUCE program [32] .
The spacetime (14) has the same weak limit as the metric obtained by Frutos-Alfaro et al. [32] . A comparison of the exterior Hartle-Thorne metric (15) with the weak limit of the metric (14) shows that upon defining
![]() (16)
(16)
both metrics coincide up to the order![]() . Hence, the metric (14) may be used to represent a compact astrophysical object. Moreover, Berti et al. [46] compared the Hartle-Thorne metric with Manko solu- tion and a numerical solution of the EFE finding that this Hartle-Thorne approximation is very reliable for most astrophysical applications. Our metric has no approximation in the rotation terms as in this metric, this could be advantageous for astrophysical problems. The first approximate solution was obtained by Sato and Tomimatsu [47] and the second one by Hernández [48] . These solutions do not have a simple form as the metric we pre- sented here.
. Hence, the metric (14) may be used to represent a compact astrophysical object. Moreover, Berti et al. [46] compared the Hartle-Thorne metric with Manko solu- tion and a numerical solution of the EFE finding that this Hartle-Thorne approximation is very reliable for most astrophysical applications. Our metric has no approximation in the rotation terms as in this metric, this could be advantageous for astrophysical problems. The first approximate solution was obtained by Sato and Tomimatsu [47] and the second one by Hernández [48] . These solutions do not have a simple form as the metric we pre- sented here.
5. Conclusions
The new Kerr metric with quadrupole moment was obtained by solving the EFE approximately. It may represent the spacetime of a rotating and slightly deformed astrophysical object, which is possible since it can match an interior solution. We showed this by comparison of our metric with the exterior Hartle-Thorne metric. The limit- ing cases for the new Kerr metric correspond to the Kerr metric, the Erez-Rosen-like metric, and the Schwarz- schild metric as expected.
The inclusion of the quadrupole moment in the Kerr metric is more suitable for astrophysical calculations than the Kerr metric alone and there are a large variety of applications which can be tackled with this new metric. Amongst the applications for this metric are astrometry, gravitational lensing, relativistic magnetohydrodynamic jet formation, and accretion disks in compact stellar objects, additionally we would like to point out that pre- vious works in superfluid neutron stars can be repeated using this new metric instead of the Hartle-Thorne me- tric as an exterior solution. Furthermore, existing software with applications of the Kerr metric can be easily modified to include the quadrupole moment.
Acknowledgements
We thank H. Quevedo for reading the manuscript.
Appendix
The non-null Ricci tensor components for the metric (8) are given by (with the tilde over ![]() dropped)
dropped)
![]()
![]()
![]()
![]()
![]()
![]()
Calculation of the scalar curvature (with the tilde over 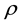 dropped)
dropped)
