Prediction and Derivation of the Hubble Constant from Subatomic Data Utilizing the Harmonic Neutron Hypothesis ()
1. Introduction
1.1. The Hubble Constant
Hubble’s law refers to the observation that objects at greater than 10 megaparsecs have a Doppler shift interpretable as a relative velocity. The Doppler shift is most commonly quoted as a velocity in (km/s)/Mpc. Galaxies appear to be moving at a rate proportional to their distance from the Earth. This is typically interpreted as evidence of the expansion of the Universe. A high precision Hubble constant H0, is an important physical constant, [1] -[6] . Hubble’s Law relates a velocity to H0 as a proportionality constant with units of s−1 times the proper distance, D. The reciprocal of H0 is the Hubble time. The reported velocities at one Mpc vary with the model and published values include: 76.9+3.9−3.4+10.0−8.0 km・s−1・Mpc−1, 69.32 ± 0.80 km・s−1・Mpc−1, 74.3 ± 2.1 km・s−1・Mpc−1, 67.3 ± 1.2 km・s−1・Mpc−1, Table 1, [1] -[6] . The methods, probes, of measurement and derivation of the H0 are different. This leads to divergent estimated values based on the methods and model. The methods include the Hubble telescope, Chandra and Sunyaev-Zeldovich Effect data from the Owens Valley Radio Observatory and the Berkeley-Illinois-Maryland Association interferometric arrays, Wilkinson Microwave Anisotropy Probe, and cosmic microwave background, CMB, temperature and lensing-potential power spectra The experimental Hubble rates range from 2.18(4) × 10−18 s−1 to 2.49(12) × 10−18 s−1. The reported Hubble time, 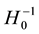 , equals approximately 4.35 × 1017 s or 13.8 byr. The approximate Hubble length equals
, equals approximately 4.35 × 1017 s or 13.8 byr. The approximate Hubble length equals 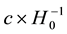 or 13.8 blyr. In this model the predicted H0 is assumed to be present experimental value with an
or 13.8 blyr. In this model the predicted H0 is assumed to be present experimental value with an 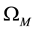 of 0.
of 0.
1.2. The Goals
The goal of this work is to derive a high precision H0, and subsequently a Hubble length, and Hubble time from natural unit frequency equivalents as integer sets of the neutron, 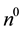 ,
, 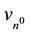 ,
, ; the hydrogen ionization energy; the Rydberg constant R,
; the hydrogen ionization energy; the Rydberg constant R,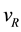 ; the Bohr radius
; the Bohr radius ,
,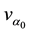 ; and the electron, e,
; and the electron, e,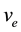 ; and the finite integer and harmonic integer set of N12
; and the finite integer and harmonic integer set of N12  and
and ![]() the harmonic fractions
the harmonic fractions ![]() [7] -[14] . N12 are referred to as integer fraction exponents,
[7] -[14] . N12 are referred to as integer fraction exponents,![]() . Another goal is to demonstrate that experimental Planck time squared,
. Another goal is to demonstrate that experimental Planck time squared, ![]() and H0 follow a previously predicted power law relationship used to derive
and H0 follow a previously predicted power law relationship used to derive![]() . [9] The proportionality constants of
. [9] The proportionality constants of![]() , and H0 ratios with
, and H0 ratios with ![]() are derived, and compared to the known experimental values.
are derived, and compared to the known experimental values.
1.3. The Harmonic Neutron Hypothesis (HNH)
The following is a review and explanation of the harmonic neutron hypothesis. It was initially copyrighted in 2006 and published in 2009, [7] -[14] . All of the physical constants are evaluated as frequency equivalents, and secondarily as dimensionless coupling constant ratios in an exponential integer or integer fraction system. Any single physical unit could be utilized, but Hertzian frequency (Hz) was arbitrarily chosen since the whole physical
system can logically be evaluated as a unified quantum spectrum. The primary natural unit is![]() . All possible physical values are defined by
. All possible physical values are defined by ![]() and integer fractions. The unit system of the HNH is maximally simplified with the units for Planck’s constant, charge, and speed of light all equaling 1. Energy, mass, frequency, temperature are all equal. The distance is 1 divided by frequency. The speed of light equals
and integer fractions. The unit system of the HNH is maximally simplified with the units for Planck’s constant, charge, and speed of light all equaling 1. Energy, mass, frequency, temperature are all equal. The distance is 1 divided by frequency. The speed of light equals ![]() times the dis-
times the dis-
tance![]() , Compton radius of the neutron. The maximum Lorentz factor equals
, Compton radius of the neutron. The maximum Lorentz factor equals![]() . Velocity squared is
. Velocity squared is![]() .
.
The primary hypothesis is that the fundamental constants are inter-related by simple, ubiquitous mathematical and geometric integer patterns. The first twelve integers, N12, and their harmonic fractions, ![]() , provide the basis for a coherent theory defining the first generation of bosons and particles, used in a power law computation for defining physical phenomena, Table 2. The model utilizes the dimensional analysis methods of Rayleigh’s method and the Buckingham Pi Theorem, where the exponential base is the dimensionless neutron annihilation frequency, Hz-s,
, provide the basis for a coherent theory defining the first generation of bosons and particles, used in a power law computation for defining physical phenomena, Table 2. The model utilizes the dimensional analysis methods of Rayleigh’s method and the Buckingham Pi Theorem, where the exponential base is the dimensionless neutron annihilation frequency, Hz-s, ![]() ,
, ![]() , and the exponents are combinations of 1 plus or minus
, and the exponents are combinations of 1 plus or minus![]() . Buckingham’s pi theorem states that physical laws are independent of the form of the physical units. Therefore, acceptable laws of physics are homogeneous in all dimensions.
. Buckingham’s pi theorem states that physical laws are independent of the form of the physical units. Therefore, acceptable laws of physics are homogeneous in all dimensions.
The Equality Pair Transformations (EPTs) inter―relate matter, electromagnetic energy, and kinetic energy transformations. EPT are common physical phenomena that can be described by Feynman diagrams, but necessitate a definitional approach when utilized in this model. Each EPT is associated with a point transformation from one state to another, or from one force to another, such as, kinetic energy to electromagnetic energy, electromagnetic energy to matter, or vice-versa. This occurs when there is a scale equality of two different states or forces. The pair is identically scaled phenomena, but can represent two different dual (paired) physical manifestations of different forces or states. This is the essence of particle-wave duality paradox. Examples are matter-antimatter pair production or annihilation; or the transformation of electromagnetic energy to kinetic energy as in the photoelectric effect. Not only is there a conservation-equality of total energy-matter, but also a transformation of state or force. These transformations are always associated with symmetric pairs.
![]()
Table 2. First generation particles and bosons. Table 2 lists the first generation physical constants related to neutron beta decay, nie, nife, and the partial harmonic fractions associated with![]() ,
,![]() . There is no physical entity associated with the nife, 9.
. There is no physical entity associated with the nife, 9.
The primary fundamental EPT scaling HNH is neutron anti-neutron pair production, and is the scaling factor used to derive further observable phenomena. The fundamental EPT ratio set is composed of a natural physical unit as a consecutive integer series representing the transformation of electromagnetic energy into frequency multiples matter associated with neutron/anti-neutron pair production. The integrally spaced dimensionless elements, vf in Vf, are based on the ratio of the respective annihilation frequencies of that physical constant to that of the neutron. At the point where the photon integer frequency series has enough energy to be scaled identically with elemental neutral matter equivalent represents the fundamental EPT. The series restarts again at 1 with each integer representing the number of nucleons in elemental matter or groups of nucleons at the EPT of pair production point. Elements in the set Vf scale all of the possible physical phenomena under consideration.
1.4. The Empirical Observations Leading to the HNH
The neutron annihilation frequency, ![]() , is the fundamental coupling constant, and the basis for EPTs on the set Vf. We assume that there exists a gravitational binding energy of the electron to the proton in hydrogen, equally as important to the units of gravitational energy, as the ionization energy of hydrogen is to the electromagnetic force. The genesis of this hypothesis was based on the empirical observation that there are integer exponent relationships of
, is the fundamental coupling constant, and the basis for EPTs on the set Vf. We assume that there exists a gravitational binding energy of the electron to the proton in hydrogen, equally as important to the units of gravitational energy, as the ionization energy of hydrogen is to the electromagnetic force. The genesis of this hypothesis was based on the empirical observation that there are integer exponent relationships of ![]() between the twice the frequency equivalent of the gravitational binding energy of the electron in hydrogen, the energy of Planck’s constant, h-Hz, and the frequency equivalent of the neutron.
between the twice the frequency equivalent of the gravitational binding energy of the electron in hydrogen, the energy of Planck’s constant, h-Hz, and the frequency equivalent of the neutron.
Twice the frequency equivalent of the gravitational binding energy of the electron in hydrogen, 2 × 2.90024(22) × 10−24 Hz equals 5.80048(44) × 10−24 Hz. We label here the gravitational binding energy of the electron in hydrogen as the elemental graviton. The frequency equivalent of Planck’s constant, h, is 1 Hz. Here,
![]() Hz is 2.271859078(50) × 1023 Hz. The reciprocal of
Hz is 2.271859078(50) × 1023 Hz. The reciprocal of ![]() is 4.4016815(1) × 10−24, and is almost iden-
is 4.4016815(1) × 10−24, and is almost iden-
tical to twice the binding gravitational frequency of the electron in hydrogen.
The factor two in the gravitational binding energy of the electron to the proton arises from the fact that it is a kinetic energy. This “2” has the same origin as the “2” in the Schwarzschild radius equation, ![]() , and both transform kinetic energy into an electromagnetic equivalent. This is also the “2” associated with an equality “pair”. All three force-state unit values are separated by a ratio of
, and both transform kinetic energy into an electromagnetic equivalent. This is also the “2” associated with an equality “pair”. All three force-state unit values are separated by a ratio of ![]() Each represents unit step values for elemental gravitational kinetic, electromagnetic, and the elemental strong nuclear forces. The frequency
Each represents unit step values for elemental gravitational kinetic, electromagnetic, and the elemental strong nuclear forces. The frequency
equivalent of the gravitational electron binding energy when multiplied by ![]() equals 1.3178, and the nor-
equals 1.3178, and the nor-
malized value of 1 Hz for Planck’s constant h, times![]() , equals
, equals ![]() in Hz. The coupling constant ratios are
in Hz. The coupling constant ratios are
represented by an injective mapping of the sequence: {−1, 0, 1, 2} to exponents of ![]() Hz. These integer
Hz. These integer
exponents, are referred to as ![]() for integer exponents. Each
for integer exponents. Each ![]() is associated with a different force and state. Thus there is a discrete quantum relationship similar to blackbody spectra, and a power law. The distribution of energy over time is exponential for many physical systems including magnetic resonance relaxation.
is associated with a different force and state. Thus there is a discrete quantum relationship similar to blackbody spectra, and a power law. The distribution of energy over time is exponential for many physical systems including magnetic resonance relaxation.
Energy multiples of Planck’s constant, h, is also an integer based wavelength or frequency system. This is identical to the resonant modes of a vibrating string. Planck’s constant represents integral units of electromagnetic energy. Though h is quantum by definition, its actual physical manifestation in black body radiation appears to be continuous. When the divisions between the physical values associated with each n unit are smaller than experimental accuracy then the physical system appears to be Almost Everywhere (A.E.) continuous, but is none the less conceptually and mathematically integer-based Figure 1.
If this initial EPT observation is valid, then there logically should be a similarly scaled transformation between the unit values of the gravitational and electromagnetic forces. At ![]() integral steps of gravitational units, i.e. twice the elemental graviton, this energy could represent an electromagnetic wave with a frequency of
integral steps of gravitational units, i.e. twice the elemental graviton, this energy could represent an electromagnetic wave with a frequency of
1 Hz. At ![]() integral steps of electromagnetic units, at 1 Hz, this energy could represent a neutron, at a fre-
integral steps of electromagnetic units, at 1 Hz, this energy could represent a neutron, at a fre-
quency of ![]() Hz. At
Hz. At ![]() integral steps of nucleon units,
integral steps of nucleon units, ![]() Hz, this mass could represent the unit mass
Hz, this mass could represent the unit mass
of a black hole, at a frequency of ![]() Hz, 5.16134367(12) × 1046 Hz. This is an extremely dense from of
Hz, 5.16134367(12) × 1046 Hz. This is an extremely dense from of
matter, and must be the mass of individual unit forming a black hole analogous of neutrons forming elemental matter. This latter mass’s Compton radius is smaller than its Schwarzschild radius, and must represent the matter of a black hole.
![]()
Figure 1. Point plots of a consecutive integer series in linear, 1/n, and loge(n) formats. Figure 1 plots three different geometric, mathematical formats of the consecutive integer sequence of n from −∞ to ∞. All three of these are seen in the model, but each in the appropriate physical and mathematical context. All are discrete series of individual points. The top row is a standard linear plot which is bound on both extremes by −∞ to ∞. The middle plot is 1/n. It is bound from −1 to +1. This is the origin of the fundamental constants where there is dense clustering the closer the mass is to the neutron, and increasingly sparse at the extremes. Figure 2, Figure 3 demonstrates that a 2d unit based system is associated with these identical harmonic fraction possibilities. The lower plot is loge(n). It also extends from by −∞ to ∞. This pattern also has a pseudo-continuous appearance as n increases. For a large Vf system only those n values that are small will appear to be discrete.
1.5. Assignment of Fundamental Physical Constants to Principal Quantum Numbers, nief
In this method all of the physical phenomena are evaluated as exponents of![]() . Each physical constant is associated with an integer identical to all quantum systems. The known exponent, expk, of the base
. Each physical constant is associated with an integer identical to all quantum systems. The known exponent, expk, of the base ![]()
for any physical constant is the natural log ![]() of the frequency equivalent of that constant divided by
of the frequency equivalent of that constant divided by
![]() . This is a classic exponent base transformation. The difference between the known exponent and
. This is a classic exponent base transformation. The difference between the known exponent and
its associated partial fraction represents the δ factor.
Inspection of an integer-based exponent system of the forces/states, ![]() Hz is a linear plot in the ex-
Hz is a linear plot in the ex-
ponential domain Figures 1-4. The only other possible point values are the harmonic fractions, ±1/nife and harmonic mixed partial fractions, 1 ± 1/nife. These integer based exponents are associated with the observable fundamental constants. For this paper the only nife utilized are points in N12, since they are associated with the first generation of kinetic energies, particles, and bosons of neutron beta decay, Table 2, Table 3.
Assignment of the nife is dependent on that value fulfilling a power law relationship with the natural unit values of the first two natural integer sets. For the simplest situation the fundamental constant is related to the nife closest to 1 divided by 1 minus the exponent of the constant. If that value is positive then the partial harmonic fraction is 1 − 1/nife. If the value is negative then the partial harmonic fraction is 1 + 1/nife. This is not the greatest integer function. However, the nife value can be driven far from the closest nife value by the power law imperative or the fact that some of the constants are divided or multiple by 2. Utilizing these relationships it is possible to logically assign the physical phenomena of the neutron beta decay process to a specific partial harmonic fraction, Table 2 [7] -[14] .
The simplest sinusoidal system that is related to a consecutive integer series is the possible wavelengths and frequencies of a vibrating string. This is associated with the harmonic sequence, ![]() , and the origin of “harmonic” in the model’s name. Figure 1. Many of the properties of the model are analogous to or identical with the mathematics and physics of music. Pure number properties are important in music, and the HNH physical model such as positive or negative, even or odd, and prime, and composite. These properties also represent imperatives that define the nife of associated entities and the hierarchy of the physical constants.
, and the origin of “harmonic” in the model’s name. Figure 1. Many of the properties of the model are analogous to or identical with the mathematics and physics of music. Pure number properties are important in music, and the HNH physical model such as positive or negative, even or odd, and prime, and composite. These properties also represent imperatives that define the nife of associated entities and the hierarchy of the physical constants.
Thus, the HNH model hypothesizes that physical constants represent a multi-layered simultaneously linear and exponential inter-locking, transformational integer series, with classic harmonic properties, in both the linear and exponential domains. These types of harmonic/repeating pattern systems are remarkably unified, where if any frequency and its associated integer value are known, then an infinite number of associated possible harmonic fractions and frequencies of the system are defined in Tables 2-4, Figure 1 of reference [14] .
![]()
Figure 2. Combined integer point and exponential plot of the fundamental unit forces separated by a ratio of![]() ; multi- physical units of the X-axis. Figure 2 is an exponential plot of the multiple X-axis unit values and their associated degenerate integer possibilities for energy, mass, frequency, distance dimension, velocity, density, gravitational, EM, elemental strong, and black hole elements. Each is a series of
; multi- physical units of the X-axis. Figure 2 is an exponential plot of the multiple X-axis unit values and their associated degenerate integer possibilities for energy, mass, frequency, distance dimension, velocity, density, gravitational, EM, elemental strong, and black hole elements. Each is a series of ![]() points starting at
points starting at ![]() and n increasing from left to right. They start as individual points, red circles, but become pseudo-continuous to the right. Each force unit value is separated by a ratio of
and n increasing from left to right. They start as individual points, red circles, but become pseudo-continuous to the right. Each force unit value is separated by a ratio of![]() , red dots and vertical blue lines. The upper row represents the distances, EM wavelengths, and mass Compton radii. Points to left of
, red dots and vertical blue lines. The upper row represents the distances, EM wavelengths, and mass Compton radii. Points to left of ![]() represent possible degenerate velocity ratios
represent possible degenerate velocity ratios ![]() values, of
values, of![]() . The points to the right of
. The points to the right of ![]() represent all of the possible kinetic elemental graviton energy levels, two times the gravitational binding energy of the electron in hydrogen. Points to the right of
represent all of the possible kinetic elemental graviton energy levels, two times the gravitational binding energy of the electron in hydrogen. Points to the right of ![]() are identical to Planck’s equation E equals n Hz times h, and black body radiators. The points to the right of
are identical to Planck’s equation E equals n Hz times h, and black body radiators. The points to the right of ![]() represent the chemical periodic chart and continues to any combination of elemental masses. The points to the right of
represent the chemical periodic chart and continues to any combination of elemental masses. The points to the right of ![]() must represent highly dense element units of matter of black holes, BH.
must represent highly dense element units of matter of black holes, BH.
![]()
Figure 3. A universal harmonic 2d plane with an exponential base of 4 demonstrating the properties of a universal ratio, exponent, 1/n calculator. Figure 3 is a 2d plot of a system identical in character to the universal harmonic exponent plane, Figure 4. This is a simplified example where the Vf = 4. This is both an integer and exponential series. The number, 4, is chosen to illustrate the nature of this 2d space in a comprehensible fashion. This 2d space represents a very powerful geometry that is similar to a slide rule, but with infinite flexibility. This includes all of the possibilities that cannot be displayed on a line plot. The blue points represent the only valid integer exponents of Vf. In this case any absolute sum of an x and y vector that adds to 1 is a potentially valid integer exponent point. The only other possible valid points are those that fall on lines that connect between two integer points, blue dots. Any absolute x plus y orthogonal distance of 1 is identical to multiplying or dividing that number by 4 in the frequency domain. Therefore an absolute unit distance from the (0,0) point forms a diamond pattern. This is identical to the actual physical constants seen in Figure 4 from [7] . The exponent of Vf equals x + y at any point. The red lines are identity lines, all with the same exponent and frequency. The δ-values represent the exponent minus the x value, or (x + y) − x, and therefore equals y. The black solid and dashed lines all converge on (0,0), which equals a frequency of 1. In this specialized case these lines define vf of 1, 4, 16, and 64. The vertical dashed blue lines represent the fractional exponents of each vf of 1/2 and 2/3. The X-axis literally represents any exponent. In a continuous system any exponent of any Vf represents the intersection of a vertical line at x, and the line connecting (0,0) to any Vf value at x equals 1. The values of any point on a line in this space is defined totally from the perspective of Vf. Two points can define any ratio, and simultaneously define any δ-line. Lines not passing through (0,0) also define a well-defined pattern, but are more complicated to describe.
![]()
Figure 4. Universal 2d harmonic plane plot of the known and derived subatomic entities, ![]() , H0. Figure 4 is a universal harmonic exponent plot of the relevant physical constants. The X-axis equals the qf − 1 or sum of qfd − 1. The Y-axis is the difference between the known or derived exponents and their qfs, and δs known or derived. This is a power law test of the model. The slopes and y-intercepts of the three lines are sums and differences of the three published values. The previously published points related to h, n0, e, R,
, H0. Figure 4 is a universal harmonic exponent plot of the relevant physical constants. The X-axis equals the qf − 1 or sum of qfd − 1. The Y-axis is the difference between the known or derived exponents and their qfs, and δs known or derived. This is a power law test of the model. The slopes and y-intercepts of the three lines are sums and differences of the three published values. The previously published points related to h, n0, e, R, ![]() ,
, ![]() are plotted. These points define three lines. The electron and
are plotted. These points define three lines. The electron and ![]() define the wk-line with slope of awk and y-intercept, bwk (blue solid line). The EM line is defined by h and R (dashed blue line). The green dashed line is the derived
define the wk-line with slope of awk and y-intercept, bwk (blue solid line). The EM line is defined by h and R (dashed blue line). The green dashed line is the derived ![]() line for
line for![]() . The known
. The known ![]() point is plotted as a green dot. The derived
point is plotted as a green dot. The derived ![]() point is centered at the red circle and the derived line fit value are all superimposed. The blue points are four of the experimental values for H0 with their associated
point is centered at the red circle and the derived line fit value are all superimposed. The blue points are four of the experimental values for H0 with their associated![]() . These are plotted at the x-value of −3/4-1 since the derived qf = −3/4. The line fit of the experimental
. These are plotted at the x-value of −3/4-1 since the derived qf = −3/4. The line fit of the experimental ![]() point and the four H0 points is plotted at the green dot. The solid green
point and the four H0 points is plotted at the green dot. The solid green ![]() -line is the best fit of the experimental data and closely parallels the derived
-line is the best fit of the experimental data and closely parallels the derived ![]() -line. The experimental solid green
-line. The experimental solid green ![]() -line fit data for
-line fit data for ![]() and
and ![]() are very close to their derived values, the dashed green line, Table 1. None of the other qfs of −1/2, −5/6, or −7/8 are within orders of magnitude of the H0, and do not represent valid qfs for H0. The vertical thin red lines are associated with the hypothesized possible negative even harmonic fractions, −1/2, −3/4, −5/6, −7/8. The thick vertical red lines are the values along the wk-line used to derive the energy lost in the neutron beta decay process, qf +1/2, +3/4, +5/6, and +7/8.
are very close to their derived values, the dashed green line, Table 1. None of the other qfs of −1/2, −5/6, or −7/8 are within orders of magnitude of the H0, and do not represent valid qfs for H0. The vertical thin red lines are associated with the hypothesized possible negative even harmonic fractions, −1/2, −3/4, −5/6, −7/8. The thick vertical red lines are the values along the wk-line used to derive the energy lost in the neutron beta decay process, qf +1/2, +3/4, +5/6, and +7/8.
![]()
Table 3. List of natural units used in the derivations. Table 3 lists the published values of![]() , and the slopes and intercepts of the wk and EM lines used for the derivation of H0. These are the only natural values used for all of the derivations. See Equations (13)-(15).
, and the slopes and intercepts of the wk and EM lines used for the derivation of H0. These are the only natural values used for all of the derivations. See Equations (13)-(15).
![]()
Table 4. Comparison of derived and known proportionality constants of H0, ![]() , and n0. Table 4 is a comparison of derived and now proportionality constants of H0,
, and n0. Table 4 is a comparison of derived and now proportionality constants of H0, ![]() , and n0. The derived values fall within the range of the known values.
, and n0. The derived values fall within the range of the known values.
1.6. Previous Derivations of the HNH and the Relationship to the Derivation of the Hubble Constant
The Harmonic Neutron Hypothesis was previously used to derive the energy/matter lost in the transformation of a neutron to hydrogen, the masses of the quarks, the Higgs boson, and the Planck time [9] [10] [14] . Purely kinetic factors of neutron beta are related to the even-numbered denominators in the harmonic fractions, 1/2, 3/4, 5/6, and 7/8. It is logically hypothesized that the additive inverse partial harmonic fractions, which includes −1/2, −3/4, −5/6, and −7/8 should be related to the cosmic kinetic fundamental constants including, the![]() , cosmic microwave background radiation, CMB, and dark matter/dark energy.
, cosmic microwave background radiation, CMB, and dark matter/dark energy.
The HNH has accurately derived Planck time, ![]() , from this same sets of integers. [9] . It is also logical to hypothesize that other cosmic fundamental constants should be related to
, from this same sets of integers. [9] . It is also logical to hypothesize that other cosmic fundamental constants should be related to![]() . Our derivation shows that
. Our derivation shows that ![]() is identical to the Newtonian gravitational constant, G, in the frequency domain. The product of
is identical to the Newtonian gravitational constant, G, in the frequency domain. The product of ![]() and the frequency equivalents of two masses and distance separating them equals the gravitational binding energy as a frequency equivalent of that system. The derived values associated with the
and the frequency equivalents of two masses and distance separating them equals the gravitational binding energy as a frequency equivalent of that system. The derived values associated with the ![]() -line at the partial harmonic fractions −1/2, −3/4, −5/6, and −7/8 should be related to the cosmic kinetic fundamental constants including
-line at the partial harmonic fractions −1/2, −3/4, −5/6, and −7/8 should be related to the cosmic kinetic fundamental constants including![]() , cosmic microwave background radiation, CMB, dark matter and energy.
, cosmic microwave background radiation, CMB, dark matter and energy.
1.7. Similarities of the HNH and Magnetic Resonance Imaging
None of the individual elements of the HNH are new or radically depart from standard physics or mathematical methods. The perspective taken, the nomenclature used, and methods are not standard, but are nonetheless logically and mathematically valid. To understand this method, a significant intellectual investment is essential since it is not intuitively obvious. The model is from a global perspective very similar to magnetic resonance imaging. MRI, which was assumed to be impossible at the time of its introduction based on classical physics interpretations of optical imaging criteria, yet disproven [15] [16] . Both MRI and the HNH are spectral analysis methods. Both have two different domains that simultaneously define the identical object/system. One domain is in standard linear physical 3d space, and the other is in a mathematically transformed domain related to phase and frequency, the k-space for MRI. In this model it relates to an exponential universal harmonic plane, Figures 2-4. Both represent the identical physical system, but are defined in different mathematical terms.
1.8. Why the Harmonic Neutron Hypothesis Is Based on Classical Physics and Not Numerology
The standard components of the HNH will be highlighted in italics. The HNH model is not in conflict with the Standard Model or overturns its methods or tenants. The actual physical values used are equivalent to standard unit values, but they are all transformed into frequency; harmonic fraction plus![]() ; or exponential equivalents. They are evaluated as dimensionless coupling constant ratios, and proportionality constants. For example the ratio of the mass of the electron divided by the mass of the neutron equals the frequency equivalent of the electron divided by the frequency equivalent of the neutron independent of unit.
; or exponential equivalents. They are evaluated as dimensionless coupling constant ratios, and proportionality constants. For example the ratio of the mass of the electron divided by the mass of the neutron equals the frequency equivalent of the electron divided by the frequency equivalent of the neutron independent of unit.
This model is independent of any specific physical unit system. Converting the standard units to this unit 1 format does not change the absolute ![]() integer value, The reason for this non-intuitive mathematical imperative is that any arbitrary mass unit changes the arbitrary Avogadro’s number,
integer value, The reason for this non-intuitive mathematical imperative is that any arbitrary mass unit changes the arbitrary Avogadro’s number, ![]() , canceling out any effect of the initial mass unit. Transforming the arbitrary distance, time, and speed of light units to 1 are canceled out by changing the unit distance ratio with the fixed Compton radius, and changing the time unit to 1. Time and distance in the speed of light are proportional so the changes parallel each other, and cancel out any choice of those initial arbitrary values.
, canceling out any effect of the initial mass unit. Transforming the arbitrary distance, time, and speed of light units to 1 are canceled out by changing the unit distance ratio with the fixed Compton radius, and changing the time unit to 1. Time and distance in the speed of light are proportional so the changes parallel each other, and cancel out any choice of those initial arbitrary values.
The combined components of the hypothesis are controversial because they are not well understood, are different from standard nomenclature, and novel. The concepts and mathematics are actually not complicated, but require a significantly different conceptual approach. All of the physical relationships are viewed solely as ex-
ponents (integer fractions plus![]() ) or ratios of
) or ratios of![]() .In the linear domain these are ratios, coupling con-
.In the linear domain these are ratios, coupling con-
stants/proportionality constants. One example would be the ratio of the frequency equivalent of the ionization energy of hydrogen divided by the frequency equivalent of the Bohr Radius, ![]() [11] . This is equivalent to Coulomb’s constant in the frequency domain.
[11] . This is equivalent to Coulomb’s constant in the frequency domain.
All of the ratios are scaled by ![]()
![]() , and therefore proportionality constants. Therefore, in this paper there should be a derivable proportionality constant that inter-relates
, and therefore proportionality constants. Therefore, in this paper there should be a derivable proportionality constant that inter-relates![]() ,
, ![]() , and H0, Table 4. Presently there is no known proportionality constant relating these three physical constants.
, and H0, Table 4. Presently there is no known proportionality constant relating these three physical constants.
In this model the identical consecutive integer and harmonic fraction sequences are seen, as exponents of the fundamental frequency, ![]() , of the system, Figures 1-3. The origin of this exponential pattern is not from a standing wave sinusoidal pattern, but from a consecutive integer exponential sequence defining the forces. In this type of ratio system, when
, of the system, Figures 1-3. The origin of this exponential pattern is not from a standing wave sinusoidal pattern, but from a consecutive integer exponential sequence defining the forces. In this type of ratio system, when ![]() is raised to an exponent in the sequence, the results represent the only possible observable frequencies of the derived or known physical constants. When this sequence of points is plotted on a 2d-plane, the only possible exponents are the integer, the harmonic fraction, and the partial fractional sequence of 1/n and 1 ± 1/n, where n equals N12, Figure 3, Figure 4. The resulting 2d-plane represents a universal 2d-exponential “slide rule”, Figure 3 [17] .
is raised to an exponent in the sequence, the results represent the only possible observable frequencies of the derived or known physical constants. When this sequence of points is plotted on a 2d-plane, the only possible exponents are the integer, the harmonic fraction, and the partial fractional sequence of 1/n and 1 ± 1/n, where n equals N12, Figure 3, Figure 4. The resulting 2d-plane represents a universal 2d-exponential “slide rule”, Figure 3 [17] .
The hypothesis is based on classic harmonic fractions, ![]() and partial harmonic fractions, 1 ± 1/n for
and partial harmonic fractions, 1 ± 1/n for![]() . This offers a tremendously powerful, predictive attribute of the model since associating a physical constant with a specific harmonic fraction creates a series of other discrete harmonics and characterizes the whole system from an initial two-element data set. This is how H0 can be derived with no direct physical measurement. An analogy is Moseley’s law on ion emission spectra.
. This offers a tremendously powerful, predictive attribute of the model since associating a physical constant with a specific harmonic fraction creates a series of other discrete harmonics and characterizes the whole system from an initial two-element data set. This is how H0 can be derived with no direct physical measurement. An analogy is Moseley’s law on ion emission spectra.
Another important concept is resonance and products of harmonic numbers. Resonance is the tendency of a system to oscillate with greater amplitude at some frequencies rather than at others. If two systems have common frequency components there will be greater coupling and potential transfer of energy between them. For a musical example, two prime number frequencies can only resonant at the product of the two prime frequencies. This pure number property defines a higher order hierarchy of physically associated entities.
The HNH presents itself as a natural unit system. A natural unit system incorporates known physical units rather than arbitrary units. A natural unit model with all of the other constants driven to 1 greatly simplify the mathematics. This model is based on the annihilation frequency of the neutron, as the fundamental frequency similar to Planck units. In Planck units all of the different fundamental constants are converted into a single common standard unit such as Hz, seconds, kilograms, or meters. The neutron is a logical unified fundamental physical entity that is centered between atomic, subatomic, and cosmic entities.
1.9. Why ![]() Are Not the Exact Fundamental Constants’ Physical Values, and Why Are δ-Values Essential?
Are Not the Exact Fundamental Constants’ Physical Values, and Why Are δ-Values Essential?
In the simplest exponential harmonic series, all of the possible frequency values could be defined and related solely to a single fundamental frequency and the harmonic fraction series, Figure 2, Figure 3 [14] . The HNH and physical reality are far more complicated. This arises from a mathematical imperative. Known fixed number values of the products of 2 and pi are associated with specific exponent integer-fraction values. These arise from the product ratio relationships of R, ![]() , e, and,
, e, and, ![]() [11] .
[11] .
There are four product ratio relationships of these entities associated with the hydrogen atom. For example the
integer fraction associated with 2 must be related to ![]() raised to (10/1155). Also 2pi must be related to
raised to (10/1155). Also 2pi must be related to ![]() raised to (39/1155). Additionally, 2 raised to (1/(10/1155)) is 5.8744 × 1034, and (2pi) raised to
raised to (39/1155). Additionally, 2 raised to (1/(10/1155)) is 5.8744 × 1034, and (2pi) raised to
(1/(39/1155)) is 4.34916 × 1023. There is no common fundamental frequency that can fulfill these conflicting mathematical imperatives. Nature’s solution is to have small δ-values added to the quantum harmonic fractions that “shim” these various values to a common fundamental frequency, in this case ![]() Hz. These δ-values represent the known or derived exponent minus the harmonic fraction. This makes the system more complicated, but fulfills the imperative of a resonant system.
Hz. These δ-values represent the known or derived exponent minus the harmonic fraction. This makes the system more complicated, but fulfills the imperative of a resonant system.
1.10. Computations Using the Universal Harmonic 2d Exponential Plane
Each physical constant is plotted as a harmonic fraction minus one on the X-axis and the Y-axis is the plot of δ (the exponent minus the harmonic fraction), Figure 3, Figure 4. This is described as the universal harmonic plane. It is universal since it can perform any ratio, product, or power calculation, and all of the physical constants are plotted on this common 2d space. [7] [14] [17] . It is harmonic since the X-axis is defined by sums and differences of integers and harmonic fractions only.
The physical datum of each point has the identical value as its standard exponent, and can be translated to its standard routine physical value. The difference between two points on the 2d universal plane represents a proportionally constant, a ratio in the linear domain, a power law. This harmonic plane also has all of the classic mathematical properties of lines. A line connecting any two points can define a proportionality relationship of two or more physical constants. It is possible to derive any harmonic value from the slope and y-intercept of a
δ-line and![]() , if the harmonic fraction is known or derived. Different forces can be associated with different
, if the harmonic fraction is known or derived. Different forces can be associated with different
or common δ-lines.
1.11. Derivation of Experimentally Unmeasured Physical Constants
In Physics, under most circumstances if one knows a natural unit within a ratio or product relationship that value can be used as a constant, but it does not have inherent predictive value to other multiple other related physical constants. In a harmonic system if the natural unit is known and its associated quantum integer value then an infinite series of other values/constants, can potentially be derived. [14] This is a classic property or quantum spectrum.
Many of these constants can be derived since the actual δ-values can be derived from the three finite point sets described above sets, provided the harmonic fraction is logically derived. [7] . The data define two lines on
the universal harmonic plane. Their slopes and y-intercepts along with ![]() are all that is necessary to derive
are all that is necessary to derive
many of the other physical constants in this model. One line is related to the weak kinetic entities, and one related to the electromagnetic entities. The only other possible valid force δ lines are related to sums and differences of the slopes and y-intercepts of those two lines, Figure 4. Harmonic fractions, other than the very limited set used here, opens the possibility to derive the actual δ-values since they would represent just another point on a valid line following the power law and quantum spectrum properties.
1.12. Value of the HNH Method and New Insights into the Meaning and Origin of Hubble’s Constant
The value of the HNH method is that it can derive and predict physical constants beyond what can be experimentally measured [9] [10] [14] . The Standard Model today cannot unify or scale quantum and cosmic phenomena simultaneously. The HNH also demonstrates the inter-relationship of the constants. The derived values have high precision since the calculations are based on high precision atomic data to begin with, and not on experimental data related to the physical constant in question [14] . In the present paper no astronomical data is utilized in the derivation of H0.
The methodology of HNH derivation generates new insights into connections between the subatomic entities of neutron beta decay, kinetic energy, and the neutrinos, leading to frequency expressions of the neutron, tP, gravity, H0; and the apparent expansion of the universe.
2. Methods and Results
2.1. Conversion of Physical Constants to Frequency Equivalents
Floating point accuracy is based upon known experimental atomic data, of approximately 5 × 10−8. All of the known fundamental constants are converted to frequency equivalents, ![]() ,
, ![]() , for the four (4) physical constants used in the HNH derivation of H0. Equations (1)-(4), Table 3. The masses are converted by multiplying by c2 (speed of light squared) then dividing by h (Planck’s constant). The distances are converted by dividing the wavelength into c. Energies in Joules are converted by dividing by h. The eV value for the neutron is 939.565378(21) × 106. Its frequency in Hz is converted to eV by multiplying by the constant, 4.13566750(21) × 10?15 eV/Hz. The eV was converted to frequency by multiplying by the constant 2.41798930(13) × 1014 Hz/eV. NA is Avogadro’s number, 6.02214129(27) × 1023 mol−1. Converting the standard units to where they are all 1’s does not change
, for the four (4) physical constants used in the HNH derivation of H0. Equations (1)-(4), Table 3. The masses are converted by multiplying by c2 (speed of light squared) then dividing by h (Planck’s constant). The distances are converted by dividing the wavelength into c. Energies in Joules are converted by dividing by h. The eV value for the neutron is 939.565378(21) × 106. Its frequency in Hz is converted to eV by multiplying by the constant, 4.13566750(21) × 10?15 eV/Hz. The eV was converted to frequency by multiplying by the constant 2.41798930(13) × 1014 Hz/eV. NA is Avogadro’s number, 6.02214129(27) × 1023 mol−1. Converting the standard units to where they are all 1’s does not change![]() .
.
![]()
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
All of the data for the fundamental constants were obtained from the websites (http://physics.nist.gov/cuu/Constants/ and www.wikipedia.org. The NIST site http://physics.nist.gov/cuu/Constants/energy.html has an online physical unit converter that can be used for these types of conversions.
2.2. The Frequency Equivalent and Exponential Domains; Calculation of Known Exponents, expk, nifek, qfk, and Known δk Values from Frequency Equivalents
This model has two parallel domains both describing the identical physical values. One domain is the frequency
equivalent of any physical value. The other domain is the exponent of the base![]() ,which when raised to
,which when raised to
that exponent equals the frequency equivalent of that specific value. Equation (5). The known exponent, expk, of
a fundamental constant is the ratio of the loge of the frequency equivalent, nks, divided by the![]() , Equation (5). Here,
, Equation (5). Here,![]() . Subscript k denotes a known experimental value and
. Subscript k denotes a known experimental value and
subscript d represents a derived value.
![]() (5)
(5)
Every value in the physical domain is defined completely in terms of its ratio and exponent relationship with
![]() . All other constants are 1. Each domain describes the identical physical value, but one does so in the
. All other constants are 1. Each domain describes the identical physical value, but one does so in the
standard physics linear/frequency domain, and the other in the exponential domain which is unique to the HNH model. The value of viewing the fundamental constants in the exponential domain is that their harmonic integer inter-relationships are clearly defined. The other is that any physical relationship can be displayed and calculated across all of the forces, and at any scale in this virtual 2d space. Despite the fact the HNH model utilizes virtual space, that space accurately defines true physical phenomena.
In the Standard Model, only a subset of physical values are quantum by definition or computational in character. In the HNH model every aspect of physical systems is quantized by integral steps. There are regions where the system appears to be experimentally continuous in the Standard Model, but this is not true in the HNH model, Figure 1. In the Standard Model there are physical values that equal 0, such as a velocity, but in the HNH this is not the case. In regions that are A.E. continuous the true quantum values can be evaluated in the HNH model.
The known expk minus the harmonic/quantum fraction, qf, equals the known δk, Equation (6). The known
frequency equivalent of a constant, vk, is calculated by raising ![]() to the expk in Equations (6). Equation (7) shows that many of the fundamental constants do not have nf equal to
to the expk in Equations (6). Equation (7) shows that many of the fundamental constants do not have nf equal to![]() , but
, but![]() .
.
![]() (6)
(6)
![]() (7)
(7)
The nife (integer-fractional exponents, “ife”) and the associated quantum fractions, qf, the harmonic fractions, and the partial harmonic fractions must fulfill a power law relationship with a natural unit constant. The closest nife to the experimental value is derived from the expk, Equations (8), but that value may not be the actual nife since it may not fulfill a power law relationship [10] . The first nife assignments from 1 to 12 are listed in Table 2. The higher principal quantum number values are harder to assign unless the constant is known with a high precision. There have been errors in assignment in the past, for example, the strange quark was initially assigned to the qf 29/30, but later corrected to 27/28, [10] [14] .
![]()
![]() (8)
(8)
2.3. Association of Individual Physical Constants to Harmonic Fractions and Their Degenerate Frequency Equivalents
As ![]() is raised to exponents of a consecutive harmonic quantum fraction
is raised to exponents of a consecutive harmonic quantum fraction ![]()
![]() for
for
![]() it represents many of the degenerate exponent values of the fundamental constants, Equations (9)-(11). The degenerate ratios of the constant’s frequency when divided by
it represents many of the degenerate exponent values of the fundamental constants, Equations (9)-(11). The degenerate ratios of the constant’s frequency when divided by ![]() represent
represent ![]() raised to the quantum fractions qf, where the harmonic quantum fraction exponents equal 1/±n where the natural number,
raised to the quantum fractions qf, where the harmonic quantum fraction exponents equal 1/±n where the natural number,![]() . These represent the degenerate proportionality constants relating
. These represent the degenerate proportionality constants relating ![]() to the degenerate n value.
to the degenerate n value.
![]() for principal quantum number
for principal quantum number ![]() to ∞ (9)
to ∞ (9)
![]() for principal quantum number (10)
for principal quantum number (10)
![]() for principal quantum number (11)
for principal quantum number (11)
Equation (12) calculates the X-axis value for a specific quantum fraction, partial fraction, and nife.
![]() (12)
(12)
2.4. Calculation of Known Exponents, expk and δk Values for n0, e, α0, R, α−1, h
By definition the expk of the n0 is 1, and the expk of h is 0. Both have a δk of 0. All of the electromagnetic spectrum, quantized n-Hz, have an effective ![]() (i.e. degenerate). All photons are actually not degenerate, but split with a Lorentz factor of
(i.e. degenerate). All photons are actually not degenerate, but split with a Lorentz factor of ![]() for energy and Lorentz factor of
for energy and Lorentz factor of ![]() for time dilation. The other quantized numbers used for e,
for time dilation. The other quantized numbers used for e, ![]() , R,
, R, ![]() are related to the first four odd prime numbers. The frequency equivalent of the
are related to the first four odd prime numbers. The frequency equivalent of the![]() ,
, ![]() , is 5.66525639(28) × 1018 Hz; where
, is 5.66525639(28) × 1018 Hz; where ![]() is 0.80291631(05). The qf is 4/5, on the X-axis location of −1/5, with principal quantum number 5, and its
is 0.80291631(05). The qf is 4/5, on the X-axis location of −1/5, with principal quantum number 5, and its ![]() equals 2.91631043(14) × 10−3. The exponent
equals 2.91631043(14) × 10−3. The exponent ![]() of
of ![]() is 1 + 3.6453880(02) × 10−3,
is 1 + 3.6453880(02) × 10−3, ![]() 3.6453880(02) × 10−3, and
3.6453880(02) × 10−3, and ![]() of 2.76391359(14) × 1023 Hz. The y-intercept of
of 2.76391359(14) × 1023 Hz. The y-intercept of ![]() line is referred to as the b entity
line is referred to as the b entity ![]() value, in this case
value, in this case![]() .
.
The frequency equivalent of the electron ne, is 1.23558996(05) × 1020 Hz; expe is 8.6023061(06). The qf is 6/7, X-axis location of −1/7, principal quantum number, 7, and its ![]() is 3.08775982(21) × 10?3. The exponent
is 3.08775982(21) × 10?3. The exponent ![]() of e is 1 + 3.60238646(18) × 10?3, be 3.60238646(18) × 10?3,
of e is 1 + 3.60238646(18) × 10?3, be 3.60238646(18) × 10?3, ![]() of 2.7575290(01) × 1023 Hz.
of 2.7575290(01) × 1023 Hz.
The frequency equivalent of hydrogen ionization energy![]() , is 3.28984196(17) × 1015 Hz;
, is 3.28984196(17) × 1015 Hz; ![]() is 6.64365544(33). The qf is 2/3, X-axis location of −1/3, principal quantum number 3, and its
is 6.64365544(33). The qf is 2/3, X-axis location of −1/3, principal quantum number 3, and its ![]() is −2.30112231(11) × 10−3. The exponent
is −2.30112231(11) × 10−3. The exponent ![]() of R is 1 −3.45168347(17) × 10−3,
of R is 1 −3.45168347(17) × 10−3, ![]() −3.45168347(17) × 10−3,
−3.45168347(17) × 10−3, ![]() of 1.88695938(09) × 1023 Hz.
of 1.88695938(09) × 1023 Hz.
The frequency equivalent of ![]() is 1.370359991(69) × 102;
is 1.370359991(69) × 102; ![]() is 9.14882590(46) × 10−2. The qf is 1/11, X-axis location of −10/11, principal quantum number 11, and its
is 9.14882590(46) × 10−2. The qf is 1/11, X-axis location of −10/11, principal quantum number 11, and its ![]() is 5.7916811(03) × 10−4.
is 5.7916811(03) × 10−4.
2.5. Plotting, Transformation, of Known Exponents and δk Values on to the 2d Universal Harmonic Exponential Plane for n0, h, e, α0, and R
The known and derived exponents of physical constants are plotted/ transformed to the 2d universal harmonic plane. The X-axis is a multi-dimensional physical descriptor, Figures 2-4. The point (0, 0) represents the neutron since that is the exponent of ![]() Hz divided by
Hz divided by ![]() Hz. The Y-axis is the related to the difference of the known exponent minus its associated qf, Equation (6). The Y-axis is not continuous in terms of the inter-relationships of the fundamental constants either. The slopes and y intercepts of the wk and EM
Hz. The Y-axis is the related to the difference of the known exponent minus its associated qf, Equation (6). The Y-axis is not continuous in terms of the inter-relationships of the fundamental constants either. The slopes and y intercepts of the wk and EM ![]() lines also represent three “quantum” unit values though not integers. The only possible δ-values are a function of qf-1, and are discrete.
lines also represent three “quantum” unit values though not integers. The only possible δ-values are a function of qf-1, and are discrete.
The points for the e, ![]() and
and ![]() fall above the X-axis since their
fall above the X-axis since their ![]() are positive. Their respective X-axis values are −1/7 = (6/7 − 1), −1/5 = (4/5 − 1), −10/11 = (1/11 − 1). The point for R falls below that X-axis at x equals −1/3 = (2/3 − 1) since the
are positive. Their respective X-axis values are −1/7 = (6/7 − 1), −1/5 = (4/5 − 1), −10/11 = (1/11 − 1). The point for R falls below that X-axis at x equals −1/3 = (2/3 − 1) since the ![]() is negative. The differences between these points on the universal harmonic exponent plane represent the classic ratios of these same values in the frequency domain [12] .
is negative. The differences between these points on the universal harmonic exponent plane represent the classic ratios of these same values in the frequency domain [12] .
2.6. Calculation of Derived Exponents, expd, Derived δd Values; and Calculation of Derived δd Slopes and Intercepts at x = −1 and x = 0
The only possible derived exponents are discrete since the only possible qf and ![]() values are discrete. The lines described below transpose the natural unit sets to the harmonic 2d plane. The line connecting the e,
values are discrete. The lines described below transpose the natural unit sets to the harmonic 2d plane. The line connecting the e, ![]() , and
, and![]() ,
, ![]() , points is logically related to the weak kinetic force,
, points is logically related to the weak kinetic force, ![]() -line. Here,
-line. Here, ![]() is a distance and related to a length dimension and velocity, therefore kinetic properties. The electron is a mass related to the weak force. The other 1/±n points on the wk line represent the other possible derived
is a distance and related to a length dimension and velocity, therefore kinetic properties. The electron is a mass related to the weak force. The other 1/±n points on the wk line represent the other possible derived ![]() s that are logically related to the weak force. These possibilities graphically represent the intersection points of the
s that are logically related to the weak force. These possibilities graphically represent the intersection points of the ![]() line with x values of ±1/n. The slope is awk, 3.000364286(15) × 10−3 and the y-intercept is bwk, 3.51638329(18) × 10−3, Equations (13), (14).
line with x values of ±1/n. The slope is awk, 3.000364286(15) × 10−3 and the y-intercept is bwk, 3.51638329(18) × 10−3, Equations (13), (14).
![]() (13)
(13)
![]() (14)
(14)
These derived ![]() values when proposed had no known physical significance. [7] It was assumed that these other “possible valid” harmonic fraction points along a
values when proposed had no known physical significance. [7] It was assumed that these other “possible valid” harmonic fraction points along a ![]() line are identical in concept and physical reality to other possible “spectral lines” in a standard quantum spectrum where each spectral line is associated with a different quantum integer. In the interval these hypothesized
line are identical in concept and physical reality to other possible “spectral lines” in a standard quantum spectrum where each spectral line is associated with a different quantum integer. In the interval these hypothesized ![]() points have been shown to be associated with many known physical entities. [9] [10] [14]
points have been shown to be associated with many known physical entities. [9] [10] [14]
The EM, line is defined by the points for the Planck constant, (−1, 0) and Rydberg R![]() , Figure 4, Equation (15). This is the second line that was previously published, [7] . This is logical since h is the unit for electromagnetic energy, and R is the unit for the atomic ionization energy. It is referred to as the electromagnetic, EM
, Figure 4, Equation (15). This is the second line that was previously published, [7] . This is logical since h is the unit for electromagnetic energy, and R is the unit for the atomic ionization energy. It is referred to as the electromagnetic, EM ![]() -line. Its slope and y-intercept, bem, are identical and equal to −3.45168347(17) × 10−3, Equation (15). This line is related to the principal quantum number 3, qf, 2/3. The other potential qf values have also been shown to be related to the quarks and mesons, [10] .
-line. Its slope and y-intercept, bem, are identical and equal to −3.45168347(17) × 10−3, Equation (15). This line is related to the principal quantum number 3, qf, 2/3. The other potential qf values have also been shown to be related to the quarks and mesons, [10] .
![]() (15)
(15)
The derived ![]() values are a linear function of the qf-1, and the slope and y intercepts of the
values are a linear function of the qf-1, and the slope and y intercepts of the ![]() -lines. An alternate definitions of slope and y intercept are the y values at x equals 0, and −1, Equations (16). These are interchangeably equivalent, and both are used in this method, Figure 4. It is possible to predict the exact exponents of unmeasured fundamental constants from these
-lines. An alternate definitions of slope and y intercept are the y values at x equals 0, and −1, Equations (16). These are interchangeably equivalent, and both are used in this method, Figure 4. It is possible to predict the exact exponents of unmeasured fundamental constants from these ![]() lines just like it is possible to derive lines of quantum spectrum without a physical measure if its natural unit and principal quantum number are known, Equation (17), (18).
lines just like it is possible to derive lines of quantum spectrum without a physical measure if its natural unit and principal quantum number are known, Equation (17), (18).
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
2.7. Calculation and Plotting of Compound Derived Exponents, qfd, expd, and Derived δd Values
Many of the fundamental constants are compound product/ratios of other fundamental constants. Therefore ![]() is a compound of four other entities. All of the possible valid force
is a compound of four other entities. All of the possible valid force ![]() lines of these composite forces can be derived since they must represent sums and differences of the slopes and y intercepts of the wk and EM lines, bwk, awk, and bem, as in the
lines of these composite forces can be derived since they must represent sums and differences of the slopes and y intercepts of the wk and EM lines, bwk, awk, and bem, as in the ![]() -line, Equations (19), (20). [14] These are the only possible valid values in a unified harmonic system, Figure 3, Figure 4. All of the compound values are derived.
-line, Equations (19), (20). [14] These are the only possible valid values in a unified harmonic system, Figure 3, Figure 4. All of the compound values are derived.
![]() for
for ![]() to 12 and products (19)
to 12 and products (19)
![]() (20)
(20)
The compound values are plotted at their qfd − 1 X-axis values and their ![]() Y-axis values identical to the other single physical value constants, Figure 4.
Y-axis values identical to the other single physical value constants, Figure 4.
2.8. Calculation of Known and Derived Proportionality Constants
Equation (21) is the proportionality constant, known or derived ![]() or
or![]() , multiplied with
, multiplied with ![]() that is associated with another fundamental constant. Equation (22) is the basic form of this relationship used in the proportionality constant derivations.
that is associated with another fundamental constant. Equation (22) is the basic form of this relationship used in the proportionality constant derivations.
![]() (21)
(21)
![]() (22)
(22)
2.9. Calculation and Plotting of the Known Frequency Equivalent![]() , expk, δk, and 2d Point
, expk, δk, and 2d Point
The known experimental h-bar ![]() is 5.39106(32) × 10−44 s, relative error 6 × 10−5. The known experimental non h-bar
is 5.39106(32) × 10−44 s, relative error 6 × 10−5. The known experimental non h-bar ![]() is 1.35134(81) × 10−43 s, Table 1. The
is 1.35134(81) × 10−43 s, Table 1. The ![]() s2 non h-bar is 1.82611(11) × 10−86 s2. The known mean experimental non h-bar expk is −3.670879(12). The known experimental non h-bar
s2 non h-bar is 1.82611(11) × 10−86 s2. The known mean experimental non h-bar expk is −3.670879(12). The known experimental non h-bar ![]() is −1.37371(1) × 10−2. The qf of
is −1.37371(1) × 10−2. The qf of ![]() is the sum of −1, −1, −6/7, −4/5 or −128/35 or −3.657142857142. The
is the sum of −1, −1, −6/7, −4/5 or −128/35 or −3.657142857142. The ![]() point is plotted at x = −128/35 −1, which equals −163/35.
point is plotted at x = −128/35 −1, which equals −163/35.
2.10. Calculation and Plotting of the Derived Frequency Equivalent![]() , expd, δd Point, δd Line
, expd, δd Point, δd Line
The harmonic neutron hypothesis has derived a high accuracy Planck time![]() . [9] The qf for these four entities defining
. [9] The qf for these four entities defining ![]() are −1, the gravitation binding energy of the electron −1, negative qf proton, −6/7, negative qf electron; −4/5; negative qf Bohr radius. The sum equals −128/35. This is plotted at the x-value of −163/35, −128/35-1.
are −1, the gravitation binding energy of the electron −1, negative qf proton, −6/7, negative qf electron; −4/5; negative qf Bohr radius. The sum equals −128/35. This is plotted at the x-value of −163/35, −128/35-1.
The derived ![]() compound
compound ![]() line has a slope of awk ? bwk ? bem, and a y intercept of ?bwk ? bem at x equals 0, and y intercept of ?awk at x equals −1, Equations (23)-(25), Figure 4. [9] The derived
line has a slope of awk ? bwk ? bem, and a y intercept of ?bwk ? bem at x equals 0, and y intercept of ?awk at x equals −1, Equations (23)-(25), Figure 4. [9] The derived ![]() is −3.670879366(1), the
is −3.670879366(1), the ![]() is −1.3736509(1) × 10−2 and the derive
is −1.3736509(1) × 10−2 and the derive ![]() is 1.82617126(91) × 10−86 s2 relative errors of 5 × 10−8. The derived no h-bar
is 1.82617126(91) × 10−86 s2 relative errors of 5 × 10−8. The derived no h-bar ![]() equals 1.35135904(68) × 1043. The equivalent
equals 1.35135904(68) × 1043. The equivalent ![]() h-bar value is 5.39114257(27) × 10−44 s. All these values are within the known experimental values.
h-bar value is 5.39114257(27) × 10−44 s. All these values are within the known experimental values.
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
2.11. The Known Experimental Velocities, H0 s−1, expk, and δk Ranges
The known experimental velocities at Mpc−1 are 76.9+3.9−3.4+10.0−8.0 km・s−1・Mpc−1, 74.3 ± 2.1 km・s−1・Mpc−1, 69.32 ± 0.80 km・s−1・Mpc−1, 67.3 ± 1.2 km・s−1・Mpc−1, Table 1. These are converted to standard s−1 ![]() values by dividing the velocity by one Mpc, 3.085677580 × 1022 meters. These value are 2.49(12) × 10−18 s−1, 2.408(67) × 10−18 s−1, 2.24(2) × 10−18 s−1, and 2.18(4) × 10−18 s−1. Their respective expk are −7.53(12) × 10−1, −7.543(8) × 10−1, −7.556(16) × 10−1, and −7.562(3) × 10−1. The respective
values by dividing the velocity by one Mpc, 3.085677580 × 1022 meters. These value are 2.49(12) × 10−18 s−1, 2.408(67) × 10−18 s−1, 2.24(2) × 10−18 s−1, and 2.18(4) × 10−18 s−1. Their respective expk are −7.53(12) × 10−1, −7.543(8) × 10−1, −7.556(16) × 10−1, and −7.562(3) × 10−1. The respective ![]() are: −3.70(90) × 10−3, −4.33(50) × 10−3, −5.62(20) × 10−3, and lastly, −6.17(32) × 10−3.
are: −3.70(90) × 10−3, −4.33(50) × 10−3, −5.62(20) × 10−3, and lastly, −6.17(32) × 10−3.
2.12. The Known Experimental Line Fit Values for H0k and![]() , expk, δk, Slope and yk-Intercept at x = 0
, expk, δk, Slope and yk-Intercept at x = 0
A line fit of the known ![]() and
and ![]() data points was completed. The line fit
data points was completed. The line fit ![]() and
and ![]() values are respectively 1.82611(11) × 10−86 s2 and 2.33(11) × 10−18 s−1. The slope is 3.021 × 10−3, and the y-intercept at x = 0 is 3.315 × 10−4. The line fit
values are respectively 1.82611(11) × 10−86 s2 and 2.33(11) × 10−18 s−1. The slope is 3.021 × 10−3, and the y-intercept at x = 0 is 3.315 × 10−4. The line fit ![]() and
and ![]() for
for ![]() are −3.670879(12), and −1.37371(1) × 10−2. This is compared to the derived values in Table 1, Figure 4. The derived and known values correlate well.
are −3.670879(12), and −1.37371(1) × 10−2. This is compared to the derived values in Table 1, Figure 4. The derived and known values correlate well.
2.13. Derivation of the expd, δd for qf Values of −1/2, −3/4, −5/6, and −6/7 on the ![]() δd Line
δd Line
The generalized ![]() line for any qf value is Equations (26)-(28). This equation is used to derive the possible hypothesized negative value harmonic fractions of beta neutron decay, −1/2, −3/4, −5/6, −7/8. One of these is hypothesized be related to
line for any qf value is Equations (26)-(28). This equation is used to derive the possible hypothesized negative value harmonic fractions of beta neutron decay, −1/2, −3/4, −5/6, −7/8. One of these is hypothesized be related to![]() .
.
![]() (26)
(26)
![]() (27)
(27)
![]() (28)
(28)
The derived![]() , exponents, and s−1 calculated values from the
, exponents, and s−1 calculated values from the ![]() line for the possible qfs of −1/2, −3/4, −5/6, −7/8 are respectively for −1/2: −4.4681966(3) × 10−3, −5.0446820(13) × 10−1, 1.6498650(1) × 10−12 s−1, for −3/4: −5.20211263(26) × 10−3, −7.5520211(04) × 10−1, 2.2972668(2) × 10−18 s−1, for −5/6: −5.4467515(3) × 10−3, −8.3878008(4) × 10−1, 2.5652661(7) × 10−20 s−1, for −7/8: −5.5690708(3) × 10−3, −8.8056907(5) × 10−1, 2.7107717(3) × 10−21 s−1, Figure 4. The qf of −3/4 is most the associated qf of
line for the possible qfs of −1/2, −3/4, −5/6, −7/8 are respectively for −1/2: −4.4681966(3) × 10−3, −5.0446820(13) × 10−1, 1.6498650(1) × 10−12 s−1, for −3/4: −5.20211263(26) × 10−3, −7.5520211(04) × 10−1, 2.2972668(2) × 10−18 s−1, for −5/6: −5.4467515(3) × 10−3, −8.3878008(4) × 10−1, 2.5652661(7) × 10−20 s−1, for −7/8: −5.5690708(3) × 10−3, −8.8056907(5) × 10−1, 2.7107717(3) × 10−21 s−1, Figure 4. The qf of −3/4 is most the associated qf of![]() . The derived
. The derived ![]() from this method is the intercept of the
from this method is the intercept of the ![]() line at an x value of −3/4-1. This is the harmonic fraction x location of −3/4-1, −7/4. The specific derivation of these factors for
line at an x value of −3/4-1. This is the harmonic fraction x location of −3/4-1, −7/4. The specific derivation of these factors for ![]() are shown in Equations (29)-(31).
are shown in Equations (29)-(31).
![]() (29)
(29)
![]() (30)
(30)
![]() (31)
(31)
2.14. Derived Hubble Time, Hubble Length
The derived Hubble time is the inverse of![]() , 4.3529990(17) × 1017 seconds. There are 3.1556926 × 107 seconds per year. The derived Hubble time equals 13.7941161(13) × 109 years. The derived Hubble length is 13.7941161(13) × 109 light years. The reported experimental value is approximately 13.8 × 109 light years.
, 4.3529990(17) × 1017 seconds. There are 3.1556926 × 107 seconds per year. The derived Hubble time equals 13.7941161(13) × 109 years. The derived Hubble length is 13.7941161(13) × 109 light years. The reported experimental value is approximately 13.8 × 109 light years.
2.15. Comparison of Known and Derived Proportionality Constants of![]() , H0 and the Neutron
, H0 and the Neutron
The known proportionally constant of the ratio of ![]() line fit
line fit ![]() divided by
divided by ![]() is 1.02(15) × 10−41. The derived value is 1.01118370(16) × 10−41, Equation (32), Table 4.
is 1.02(15) × 10−41. The derived value is 1.01118370(16) × 10−41, Equation (32), Table 4.
![]() (32)
(32)
The known proportionally constant of the ratio from the ![]() line fit
line fit ![]() divided by
divided by ![]() is 8.03(40) × 10−110. The derived value is 8.0382241(5) × 10−110, Equation (33).
is 8.03(40) × 10−110. The derived value is 8.0382241(5) × 10−110, Equation (33).
![]() (33)
(33)
The known proportionally constant of the ratio from the ![]() line fit
line fit ![]() divided by
divided by ![]() is 1.272(64) × 1068. The derived
is 1.272(64) × 1068. The derived ![]() value is 1.25796898(7) × 1068, Equation (34).
value is 1.25796898(7) × 1068, Equation (34).
![]() (34)
(34)
3. Discussion
A robust physics model that explains many of the mysteries of today remains elusive [18] [19] . A dominant unsolved problem is how to scale sub-atomic quantum, classical physics, and cosmologic phenomena simultaneously in a coherent mathematical and physical model. The HNH answers some of these questions, and actually derives accurate values of the physical cosmological and high energy constants that cannot be accurately experimentally measured [7] -[14] .
Many critics of the HNH suspect that these findings are simply coincidence or numerology. The HNH is however a classic dimensionless physical system of the Buckingham Pi theorem type. The speed of light is finite, and constant within any setting. It is logical that the whole system should be based on a finite constant as well. The harmonic neutron hypothesis is highly restricted. Only three starting finite number sets are used. The derivations are not made directly from the original subatomic data, but from the unified scaling of the whole universal harmonic 2d plane, Figure 3, Figure 4. Therefore it is incorrect to interpret that H0 was derived from a product ratio relationship of the four subatomic constants that would be utilized in a classic physics’ method. It is impossible to manipulate the results since all of the components are fixed previously published natural units, and harmonic integer fractions. It is not possible to derive any value by manipulating the nife value. An argument by analogy is that it is not possible to derive any wavelength from the Rydberg series by changing the n1 and n2 values since R is a natural unit
The hypothesis logically states that related physical constants will naturally all fall on a single ![]() line since they are all scaled by the same proportionality constant. The derivation of H0 from the
line since they are all scaled by the same proportionality constant. The derivation of H0 from the ![]() -line is support of the hypothesis that these two are related to the same proportionality constant, Equations (32)-(34). The proportionality constants of the neutron,
-line is support of the hypothesis that these two are related to the same proportionality constant, Equations (32)-(34). The proportionality constants of the neutron, ![]() , and H0 are accurately derived. This is viewed as impossible utilizing standard methods.
, and H0 are accurately derived. This is viewed as impossible utilizing standard methods.
The typical interpretation of the H0 is that it is not felt to be a true constant, but changes with other variables defining the nature of the cosmos. It has been described as the Hubble parameter. It is experimentally impossible to prove that the H0 is actually changing from the present value. In the HNH H0 is felt to constant, and is analogous to the free space constants of permeability, and permittivity. Interpretation of quantum systems using classical physics concepts is inaccurate and inappropriate. In the HNH the same is true for cosmology phenomena.
It is logical that the H0 should be closely related to the gravitational force, and therefore![]() . H0 is related to an expansive kinetic phenomenon, and so is the neutron beta decay process. H0 and the beta decay qfs have inverse signs, 3/4 and −3/4, but identical harmonic fractions. The harmonic neutron hypothesis has shown multiple examples of this type of harmonic fraction sign symmetry with inverse sign relationships. The top quark is 1+1/10 and the up quark is 1 − 1/10. The Higgs boson is 1 + 1/11, and the down quark is 1 − 1/11. This is a non-coincidental relationship as seen with the Rydberg series and with Moseley’s law, which in the exponential domain represent inverse exponents.
. H0 is related to an expansive kinetic phenomenon, and so is the neutron beta decay process. H0 and the beta decay qfs have inverse signs, 3/4 and −3/4, but identical harmonic fractions. The harmonic neutron hypothesis has shown multiple examples of this type of harmonic fraction sign symmetry with inverse sign relationships. The top quark is 1+1/10 and the up quark is 1 − 1/10. The Higgs boson is 1 + 1/11, and the down quark is 1 − 1/11. This is a non-coincidental relationship as seen with the Rydberg series and with Moseley’s law, which in the exponential domain represent inverse exponents.
Perhaps the other qfs −1/2, −5/6, or −7/8 represent the properties of dark matter and energy. It is possible to accurately derive CMB peak spectral radiance from the same ![]() line using the partial fractions 1/2 and 2 × −3/4, −3/2. It is likely that dark matter and dark energy are related to the partial fraction −1/2. The properties of black holes can also be interrogated with the HNH without limitations of singularities since the Schwarzschild radius relationship can be evaluated using
line using the partial fractions 1/2 and 2 × −3/4, −3/2. It is likely that dark matter and dark energy are related to the partial fraction −1/2. The properties of black holes can also be interrogated with the HNH without limitations of singularities since the Schwarzschild radius relationship can be evaluated using ![]() s2. The derived
s2. The derived ![]() can be used to derive the masses and dimensions of black holes. Also the HNH has no singularities since the number
can be used to derive the masses and dimensions of black holes. Also the HNH has no singularities since the number ![]() is finite, and also represents the maximum Lorentz factor.
is finite, and also represents the maximum Lorentz factor.
The HNH also explains the precise logical origin of H0 and unification with other fundamental constants including the neutron, hydrogen, neutrinos, ![]() , G, and the kinetic energy lost in the beta decay process. The +3/4 qf is associated with kinetic energy lost during neutron beta decay. It is also associated with the muon antineutrino, as yet unpublished data. The expectation values of the neutrinos all fall on the wk line. The expectation value of the muon neutrino is related to the qf sum of 3/4 and 1/10 for the up quark on the wk line. The expectation value of the electron neutrino is related to the qf sum of 1/2 and 1/7 for the electron on the wk line. The expectation value of the Tau neutrino is related to the qf sum of 5/6 and 1/10, and for the up quark on the wk line.
, G, and the kinetic energy lost in the beta decay process. The +3/4 qf is associated with kinetic energy lost during neutron beta decay. It is also associated with the muon antineutrino, as yet unpublished data. The expectation values of the neutrinos all fall on the wk line. The expectation value of the muon neutrino is related to the qf sum of 3/4 and 1/10 for the up quark on the wk line. The expectation value of the electron neutrino is related to the qf sum of 1/2 and 1/7 for the electron on the wk line. The expectation value of the Tau neutrino is related to the qf sum of 5/6 and 1/10, and for the up quark on the wk line.
4. Conclusion
H0 can be derived from four finite integer natural units and N12. H0 is logically related by harmonic fractions to the beta decay kinetic energy based on a common harmonic fraction, 3/4, but with opposite sign. The experimental Planck time and H0 data power law data is closely linked to the predicted data. The derived H0 can be evaluated in the future to see if this is an accurate prediction. Derivation of accurate coupling constants of the neutron with ![]() and H0 has never been achieved before so this is a significant result.
and H0 has never been achieved before so this is a significant result.
Acknowledgements
I would like to thank Tom Budinger Ph.D. for his sage advice, and help. I would also like to thank Richard White MD for his support of this work.