1. Introduction
In our precursor paper [1] , we carried out Einstein’s general relativized quantum mechanics approach by re-imagining the basic geometry of local spacetime [2] . This was accomplished in an analogous way to the how Max Planck solved the blackbody radiation problem―through light quanta absorption and emission. However, instead of a perfect absorber and emitter of light, we proposed a background of fluctuating vacuum energy intermingled with gravitons. Under the principle of general relativity, vacuum energy fluctuations will induce graviton oscillations. Taken together this was enough information to construct a modified flat spacetime metric from normal coordinates describing graviton oscillations [3] . After a straightforward general relativistic calculation on the modified metric, the covariant and contravariant energy momentum tensors emerged as raising and lowering operators describing n-valued graviton excitement. From these operators, we were able to generate all three boson masses (including the Higgs mass) in precise agreement with 2010 CODATA (NIST) [4] ; moreover, accelerated spacetimes were shown to naturally manifest from this approach.
Continuing on with the general relativized quantum physics approach, in this paper, we produce an n-valued Coulombs Force Law, which leads directly to light quanta generating the atomic energy spectrum of hydrogen. We are able to accomplish this without artificially assuming, as Bohr did, quantized: momentum, radii, or velocity for the orbiting electron. Such n-valued atomic energy states emerge naturally from the general relativistic equations (acting on the modified flat spacetime metric), just as Einstein had hoped they would.
2. Energy Momentum Operators
Our general relativistic strategy is to consider flat spacetime at the microscopic level, where vacuum energy fluctuations induce graviton oscillations. Under such a scenario, no longer can the flat spacetime metric be described by the Minkowski metric:
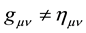 (1)
(1)
Instead, we construct a spacetime metric describing graviton oscillations, from normal coordinates [5] , i.e.,
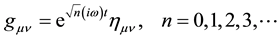 (2)
(2)
(Note, at first we did not introduce 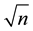 into the spacetime metric. That occurred later when we observed the contravariant energy momentum tensor was describing complex energies phasing cyclically into real and imaginary energies as a function of
into the spacetime metric. That occurred later when we observed the contravariant energy momentum tensor was describing complex energies phasing cyclically into real and imaginary energies as a function of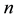 . Furthermore, when
. Furthermore, when , or when
, or when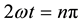 , spacetime reduces to Minkowski, and results in spacetime nodes both at the local level and then through superposition at the macroscopic level. Whereas the covariant momentum tensor generates only real energy; moreover, the covariant and contravariant operators―acting on the same point in spacetime, display constructive and destructive spacetime interference, as can be understood by:
, spacetime reduces to Minkowski, and results in spacetime nodes both at the local level and then through superposition at the macroscopic level. Whereas the covariant momentum tensor generates only real energy; moreover, the covariant and contravariant operators―acting on the same point in spacetime, display constructive and destructive spacetime interference, as can be understood by:
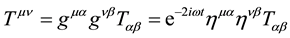 (3)
(3)
This relationship between the mass-energy momentum operators, helps to explain why ordinary matter dominates over antimatter. This is so, because, whereas the covariant energy momentum tensor is always real, the contravariant energy momentum tensor continually phases from real to complex energy-matter. Hence, the energy tensor-operators act destructively or constructively on the same spacetime point to either cancel out antimatter (except under narrow constraints between the phasing), or to add constructively to produce ordinary matter throughout the cosmos.
The following covariant and contravariant n-valued energy momentum tensor-operators were calculated directly from the general relativistic wave equations acting on the modified flat spacetime metric: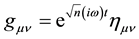 :
:
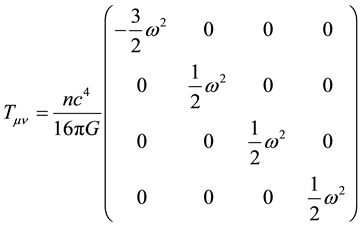 (4)
(4)
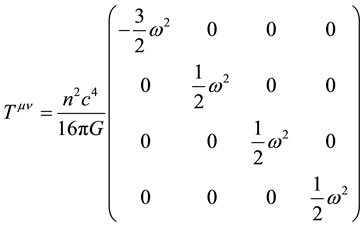 (5)
(5)
Because 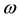 is the fundamental angular graviton frequency, the n-valued covariant and contravariant energy operators describe graviton excitement. Furthermore, this remarkable n-valued feature of spacetime, is the reason hierarchal particle mass is generated.
is the fundamental angular graviton frequency, the n-valued covariant and contravariant energy operators describe graviton excitement. Furthermore, this remarkable n-valued feature of spacetime, is the reason hierarchal particle mass is generated.
We conclude this section, by showing the energy operators obey the conservation of energy:
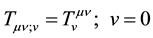 (6)
(6)
Historically, when this condition was applied to the electromagnetic equations by James Clerk Maxwell, he realized the four electromagnetic equations were not mathematically consistent. To make them consistent (so they obeyed conservation of energy), Maxwell altered Ampere’s Law. Upon so doing, he was able to solve one the greatest mystery throughout all time, that of the composition of light. Today, we understand conservation principles provide a powerful tool in ascertaining the laws and workings of natural phenomena. Just as importantly, such consistency conditions provide a means to legitimize (or negate) proposed physical theories. This was indeed the case for classical electromagnetic theory, and now for the general relativized quantum physics approach, we are applying in this paper. The most generalized consistency condition (conservation principle) for gravity interacting with all particle fields, was put into its complete and final form by J. Fang, and is referred to as the Maxwell-Fang consistency condition (MFCC) [6] -[9] .
3. Boson Mass
By assuming the two energy momentum operators described above can be detached from the general relativistic wave equations, (without losing their basic spin-like structure), and then applied to more extreme spacetime conditions where gravitons can be excited into higher energy states, in our precursor paper we were able to generate all three boson masses (including Higgs) in precise agreement with CODATA (NIST) [10] . These calculated mass values are as follows:
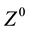 -boson mass value:
-boson mass value:
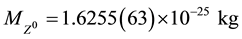 (7)
(7)
Table 1 of the CODATA (2013) reports a 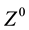 boson mass of 91.1876(21) GeV/c2, where 1 GeV/c2 = 1.782661758(44) × 10−27 kg; hence the Z-boson mass in kilograms is: 1.6255(66) × 10−25 kg. As can be seen, RQP Z-boson mass is in strong agreement with the experimental
boson mass of 91.1876(21) GeV/c2, where 1 GeV/c2 = 1.782661758(44) × 10−27 kg; hence the Z-boson mass in kilograms is: 1.6255(66) × 10−25 kg. As can be seen, RQP Z-boson mass is in strong agreement with the experimental 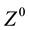 boson mass value.
boson mass value.
W-boson mass value:
![]() (8)
(8)
The CODATA reports a W-boson mass of: 1.433(32) × 10−25 kg, thus we have a second precise match with experiment.
Higgs mass value:
![]() (9)
(9)
CERN and others report a Higgs mass of 126.0 GeV or 2.246 × 10−25 kg.
All three boson masses calculated from RQP, are in precise agreement with experiment, and so offers confirmation of our general relativized quantum physics approach. Since the Standard Model for particle physics is unable to obtain these hierarchal boson mass values, this is one of the first indications that Einstein’s approach to general relativizing quantum physics (RQP), is more fundamental and successful, than is the quantum mechanical approach to nature. In addition to generating boson mass, in our precursor paper [11] , we were able to produce a set of graviton characteristic capable of generating: Planck’s constant; speed of light constant; gravitational constant; fine constant structure; electron mass; electric permeability constant, magnetic permeability constant; uncertainty principle, all in precise agreement with CODATA (NIST). The set of four graviton characteristics are denoted by:
![]() (10)
(10)
where the graviton characteristic operator ![]() is given by:
is given by:
![]() (11)
(11)
And the graviton frequency, mass and wavelength have values of:
![]() (12)
(12)
In this paper we continue on with RQP approach, and now show Coulombs Force Law becomes n-valued, leading to quantized atomic energy states for the hydrogen atom.
4. Electron Mass Generated from RQP
After detaching the covariant and contravariant energy momentum operators (calculated on modified flat spacetime), these gravitational operators were then applied to extreme spacetime, whereupon graviton excitations would naturally occur (namely inside the galactic core). The result being, that gravitons represented by the time component in the energy momentum tensor-operator, would switch sign to become repulsive, and so flux from the core at speeds near light. By assuming so, allowed us to calculate the galactic dark halo number density.
![]() (13)
(13)
By dividing this number density into the relativized energy momentum tensor-operators, yielded the energy per graviton, which we then converted into n-valued boson mass.
In this paper, we follow the same procedure, except rather than generating boson mass, we generate lepton electron mass. To do so means we need to apply a fundamental electron creation frequency to the energy momentum operators. That is to say, we replace the graviton angular frequency by the creation electron-lepton frequency: ![]() (Note: within RQP all physical values are ultimately generated from the four graviton characteristics discussed previously; and so
(Note: within RQP all physical values are ultimately generated from the four graviton characteristics discussed previously; and so ![]() serves only as intermediary step to bring clarity to the methodology of RQP). For the covariant energy tensor we have:
serves only as intermediary step to bring clarity to the methodology of RQP). For the covariant energy tensor we have:
![]() , (14)
, (14)
(Moreover, RQP allows for n-valued energy momentum operators; this is useful in explaining atomic transition frequencies [12] -[14] and any current discrepancies, however this is not the topic of this paper, and so will not be addressed in any greater detail.)
Converting this energy per particle formula into the well known electron mass:
![]() (15)
(15)
Then solving for the coefficient value:![]() , we have:
, we have:
![]() (16)
(16)
Changing notation for purposes of visual understanding![]() , we solve for the n-value that can generate electron mass:
, we solve for the n-value that can generate electron mass: ![]() ground state:
ground state: ![]() yields the value:
yields the value:
![]() (17)
(17)
From this coefficient, the general relativistic contravariant energy momentum tensor-operator, becomes n-valued mass-energy generator for electrons:
![]() (18)
(18)
What is being said here, is that, the mass-energy of an electron may become discretely elevated or reduced, due to various spacetime conditions (rather than as Bohr did, by artificially proposing quantized electron angular momentum). This RQP understanding of discrete n-valued changes in the mass-energy of an electron caused by spacetime conditions, is fundamentally congruous to a relativistic understanding―as initially described by special relativity. From a general relativistic approach, if quanta is to manifest, it must do so from causal mass- energy relationships involving spacetime. This is the key feature of RQP; in particular to bound, n-valued electron mass―leading to atomic light quanta emission and absorption.
We now apply n-valued electron mass-energy to Coulombs force law:
![]() (19)
(19)
where ![]() is the atomic number of the atom, that we set to
is the atomic number of the atom, that we set to ![]() for hydrogen. Assuming centripetal acceleration, for orbiting electrons, we have:
for hydrogen. Assuming centripetal acceleration, for orbiting electrons, we have:
![]() (20)
(20)
We now solve the n-valued atomic hydrogen energy levels. By rearranging terms, we have:
![]() (21)
(21)
This immediately yields the kinetic energy for an electron orbiting about the hydrogen nucleus:
![]() (22)
(22)
By the Virial Theorem the total energy is half the potential energy, and so the total energy is:
![]() (23)
(23)
This last energy relationship reveals quantized mass leads to n-valued energy states for the hydrogen atom (and in theory, any atom). From a relativity point-of-view, it makes far more sense that atomic spectral energies be derived from n-valued mass-energy, simply because mass and energy are fundamental aspects of Nature; and not with particular electron radii or velocity. Furthermore, RQP is able to provide a theoretical reason as to why discrete energy emission and absorption arise from n-valued mass. This is immediately understood via the relationship between the covariant and contravariant energy momentum tensor-operators, which reveal that the gravitational fields continually undergo constructive and destructive spacetime interference (while generating fundamental n-valued matter):
![]() (24)
(24)
This type of interference is different than electromagnetic wave interference; its derivative is spacetime. What this means in regards to electrons bound to the nucleus of a hydrogen atom, is that these electrons are not simply stuck in an orbiting groove. Rather one must try to imagine all the complexity of a collection of hydrogen gas molecules interacting with each other. And in this collection, for each hydrogen molecule, there also occurs electron-proton interaction. All the while, this unimaginable number comprising the hydrogen soup, consists also of electrons moving about with various velocities and orbiting radii. Yet, because of the constructive and destructive interference nature of spacetime itself, all these interacting complexities are expressed in the form of n-valued hydrogen energy absorption and emission spectra. In short, both electron position and velocity lose their significance, whereas n-valued mass becomes the predominant theme in a general relativized quantum physics theory. This means position, charge and the electron constant k, are simply parameters that may be converted to the well known empirical relationship:
![]() (25)
(25)
where h is Planck’s constant, c is the speed of light, q the charge of an electron, and R is Rydberg’s constant (all these constants derivable from the four graviton characteristics). This implies the general relativized atomic hydrogen energy values are then given by:
![]() (26)
(26)
5. Conclusion
Following Einstein’s General Relativized Quantum approach (RQP), we were able to generate an n-valued Coulombs Law [15] , which led to light quanta and the atomic hydrogen energy spectrum. In terms of relativity, and RQP theory, it makes far more sense to associate n-valued atomic energy levels with mass-energy, rather than with a particular electron radii or orbiting velocity. Furthermore, since general relativity is completely a covariant theory, this implies RQP theory (from which it is founded), has the advantage of providing new spectral predictions manifesting within extreme spacetime conditions, whereas, flat spacetime radiation theories, simply cannot. For example, there is no way for quantum mechanics to make spectral predictions within the galactic core where supermassive black hole exists. However, under the RQP schemata, this determination is possible. In fact, with the RQP energy momentum energy-operators describing constructive and destructive spacetime interference and the formation of matter and antimatter particles, it may help correct Hawking Radiation predictions [16] , so as to be in better agreement with empirical observation. Finally, we mention that we are currently calculating lepton mass from RQP theory. Taken together, RQP theory supports Einstein’s vision to have quantum phenomenon emerge from the general relativistic wave equations.
Acknowledgements
My foremost respect and gratitude goes to John Fang; a great friend and physicist whom developed Maxwell’s consistency formulation into its final and complete form for gravity interacting with all other particle fields. Fang’s consistency formulation was applied to the RQP theory presented in this paper, and thus validated the quantized Coulomb’s law resulting in the n-valued spectral emission and absorption for atomic hydrogen. I also wish to thank Stephanie Fang for her kindness, hospitality and goodness. Special thanks also goes to Kai Lam, Steven McCauley, Peter Siegel, Antonio Aurilia, Mary Mogge, Alfonso Agnew, Konrad Stein, Jim Feagin, Hedi Fearn and Harvey Leff, for their years in guiding me through the world of physics and mathematics, also thanks goes to Vann Priest in guiding me toward new approaches in teaching physics. Finally, without Natalie Valle and her little Scarlet Rembrandt (artist), life would not have been filled with so many happy and meaningful moments, providing me with the emotional courage and stamina to endure years of reflective thought leading to the General Relativized Quantum Physics approach. Parissa Djafari and Pamela Hope have provided me with much inspiration and world hope. Of course, I am indebted to my mother, Camilla Christensen, who suffered “bowtie Fenster”, and all his pet lizards and frogs, as did my grandfather, father and sons Walter and Cleo. Finally, deep respect and admiration goes to Camille Paglia, whose writings concerning art, science and religion, are invaluable to those seeking “deeper meaning”.