A Regime Switching Model for the Term Structure of Credit Risk Spreads ()
1. Introduction
When pricing of credit instruments subject to default risk, market participants typically assume that default is unpredictable, using dynamics derived from rating information in order to take advantage of credit events (cf. [1] ). Generally, they fall into a loose hierarchy known as reduced-form models. The most ubiquitous approach involving hazard rate models wherein default risk via unexpected events is modeled by a jump process. In this framework, credit-risky securities are priced as discounted expectation under the risk neutral probability mea- sure with modified discount rate (cf. [2] , [3] ). Although conceptually simple and easy to implement, these models are limited by the appropriate calibration of the hazard rate process. More generally, spread modeling represents spreads directly and eliminates the need to make assumptions on recovery (cf. [4] , [5] ). Finally, rating based models consider the creditworthiness of the issuer to be a key state variable used to calibrate the risk-neutral hazard rate (cf. [6] - [8] ). A progressive drift in credit quality toward default (an absorbing state) is now allowed as opposed to a single jump to bankruptcy, as in many hazard rate models. Rating based models are particularly useful for the pricing of securities whose payoffs depend on the rating of the issuer.
In this paper, we consider a rating based regime switching model for the term-structure of credit risk spreads in continuous time (cf. [9] , [10] ). A unique feature of our model is the inclusion of stochastic transition pro- babilities. Credit instruments are then characterized as the solution to a ultraparabolic Hamilton-Jacobi system of equations for which we develop a methods-of-lines finite difference method. Computations are presented for a rating based callable bond which validates the applicability and efficiency of the method.
2. Model of the Economy
In this section, we introduce the dynamics of the risk-less and risky term structures of interest rates as well as the bankruptcy process. To this end, we assume the existence of a unique equivalent martingale measure such that all risk-less and risky zero-coupon bond prices are martingales after normalization by the money market account (cf. [11] , [12] ). Without loss of generality, we suppose a single risky zero-coupon bond price and continuous trading over a finite time interval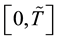 . We let
. We let 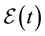
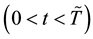 denote a continuous time Markov process on the regime (or états) space
denote a continuous time Markov process on the regime (or états) space 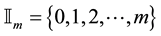 with associated transition probabilities
with associated transition probabilities
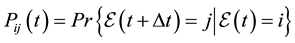 , for all
, for all ; it follows that
; it follows that
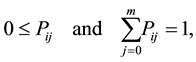 (2.1)
(2.1)
for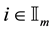 . Let
. Let 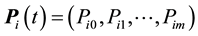 represent the
represent the 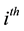 -state transition distribution.
-state transition distribution.
We define the transition probabilities as follows. The 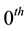 -state we associate with default, in which case
-state we associate with default, in which case 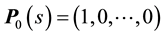 . For
. For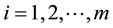 , we define the
, we define the 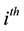 -state transition dynamics consistent with the non- negativity constraint in (2.1) such that
-state transition dynamics consistent with the non- negativity constraint in (2.1) such that 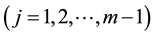
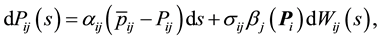 (2.2a)
(2.2a)
![]() (2.2b)
(2.2b)
for![]() , where
, where
![]()
and ![]() is the mean transition level satisfying
is the mean transition level satisfying![]() ,
, ![]() is the rate of reversion to the mean,
is the rate of reversion to the mean,
![]() and
and ![]() is a Wiener process. From (2.1), it follows that
is a Wiener process. From (2.1), it follows that ![]() and so
and so
![]() (2.2c)
(2.2c)
![]() (2.2d)
(2.2d)
We relate the transition matrix ![]() to the regime dynamics via the infinitesimal generator
to the regime dynamics via the infinitesimal generator![]() ,
,
![]()
such that
![]()
for![]() , and
, and
![]()
where ![]() is the vector of probabilities
is the vector of probabilities![]() . Without loss of generality, we associate
. Without loss of generality, we associate ![]() with the vector
with the vector![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() , subject to the dynamics
, subject to the dynamics
![]() (2.3a)
(2.3a)
![]() (2.3b)
(2.3b)
for![]() , where
, where ![]() is a martingale with respect to the filtration generated by
is a martingale with respect to the filtration generated by ![]() and
and
![]() ( [13] , Chap 4.8; [14] , Part III, App. B; [15] , Chap 8). In particular, the state of the system
( [13] , Chap 4.8; [14] , Part III, App. B; [15] , Chap 8). In particular, the state of the system
is known at inception such that![]() , for some
, for some![]() .
.
We suppose that the risky interest rate R follows a state specific Cox-Ingersall-Ross dynamic given by
![]() (2.4a)
(2.4a)
for![]() , with mean reversion level
, with mean reversion level ![]() and rate of reversion to the mean
and rate of reversion to the mean![]() , such that
, such that
![]() (2.4b)
(2.4b)
where ![]() is a Wiener process. In default
is a Wiener process. In default![]() , otherwise
, otherwise ![]() and
and![]() . The risky bond price
. The risky bond price ![]() associated with a maturity
associated with a maturity ![]() satisfies
satisfies
![]() (2.5a)
(2.5a)
![]() (2.5b)
(2.5b)
We consider the risk-less interest rate ![]() to satisfy
to satisfy
![]()
![]()
where in default ![]() for convenience, and
for convenience, and ![]() otherwise.
otherwise.
For a given contract![]() , we define the value function associated with the joint Markov ultradiffusion process (2.2)-(2.5) such that
, we define the value function associated with the joint Markov ultradiffusion process (2.2)-(2.5) such that
![]() (2.6)
(2.6)
for![]() , where
, where![]() .
.
In particular, for a non-coupon paying bond ![]() and
and ![]() otherwise, where
otherwise, where ![]() is the de- fault recovery rate, whereas for a callable bond
is the de- fault recovery rate, whereas for a callable bond ![]() and
and ![]() other- wise, for some rating based exercise price
other- wise, for some rating based exercise price![]() . Generalization of (2.6) and the subsequent analysis to include early exercise features follows routinely and will not be considered here.
. Generalization of (2.6) and the subsequent analysis to include early exercise features follows routinely and will not be considered here.
3. Characterization
Letting ![]() and
and
![]() (3.1a)
(3.1a)
we recover (2.6) succinctly as
![]() (3.1b)
(3.1b)
for![]() . By Itô’s rule, the value function (2.6) is characterized via (3.1) as the solution to the ultraparabolic Hamilton-Jacobi system of equations
. By Itô’s rule, the value function (2.6) is characterized via (3.1) as the solution to the ultraparabolic Hamilton-Jacobi system of equations
![]()
![]()
![]()
![]()
![]()
![]()
![]()
where
![]()
Let ![]() denote the temporal variable and
denote the temporal variable and
![]() the spatial, we define
the spatial, we define
![]()
and![]() , such that the above can be written
, such that the above can be written
![]() (3.2a)
(3.2a)
for all![]() , subject to the terminal constraint
, subject to the terminal constraint
![]() (3.2b)
(3.2b)
for![]() , where
, where ![]()
4. Approximation Solvability
Towards obtaining a constructive approximation of (3.2), we consider an exhaustive sequence of bounded open domains ![]() such that
such that ![]() and
and ![]() as well as a sequence of monotonically increasing real numbers
as well as a sequence of monotonically increasing real numbers![]() , as
, as![]() . Let
. Let ![]() and
and![]() , we seek
, we seek ![]() satisfying
satisfying
![]() (4.1a)
(4.1a)
for all![]() , subject to the boundary condition
, subject to the boundary condition
![]() (4.1b)
(4.1b)
for![]() , and terminal constraint
, and terminal constraint
![]() (4.1c)
(4.1c)
where![]() . As (3.2) is an infinite horizon problem in
. As (3.2) is an infinite horizon problem in![]() , we remark to the necessity of intro- ducing the artificial terminal condition
, we remark to the necessity of intro- ducing the artificial terminal condition ![]() along the frontier
along the frontier ![]() (cf. [16] ). In particular,
(cf. [16] ). In particular, ![]() as
as![]() , on any compact subset of
, on any compact subset of![]() , for any fixed
, for any fixed![]() .
.
We next place (4.1) into standard form by setting![]() ,
, ![]() ,
, ![]() , in which case
, in which case![]() . Letting
. Letting
![]()
Equation (4.1) becomes
![]() (4.2a)
(4.2a)
for all![]() , subject to the boundary condition
, subject to the boundary condition
![]() (4.2b)
(4.2b)
for![]() , and initial condition
, and initial condition
![]() (4.2c)
(4.2c)
where![]() , where
, where![]() .
.
We consider the discretization of (4.2) by the backward Euler method temporally and central differencing in
space. To this end, we introduce the temporal step sizes ![]() and mesh sizes
and mesh sizes![]() , such
, such
that ![]() and
and![]() . Spatially, we utilize the step sizes
. Spatially, we utilize the step sizes ![]() and mesh sizes
and mesh sizes
![]() ; we denote the value of
; we denote the value of ![]() on the grid by
on the grid by
![]()
where![]() ,
, ![]() ,
, ![]() ,
, ![]() , and so forth. Notationally, we let
, and so forth. Notationally, we let
![]() , where
, where![]() ,
, ![]() ,
, ![]() , and
, and
![]() . For
. For
![]()
the difference quotients are then backward first order in time:
![]()
![]()
and central second-order in space:
![]()
![]()
and so forth, and
![]()
![]()
and so forth.
Given the above, we define the method-of-lines finite difference discretization of (4.2) such that
![]() (4.3a)
(4.3a)
for all![]() , subject to the boundary condition
, subject to the boundary condition
![]() (4.3b)
(4.3b)
for![]() , and initial condition
, and initial condition
![]() (4.3c)
(4.3c)
where![]() ,
, ![]() ,
,
![]()
![]()
and![]() . We solve (4.3) utilizing the pseudo-code (cf. [16] , [17] ):
. We solve (4.3) utilizing the pseudo-code (cf. [16] , [17] ):
do ![]()
do ![]()
solve for ![]() via (4.3).
via (4.3).
5. Numerical Experiment
In this section, we present a representative computation for the valuation of a callable bond relative to three credit ratings:
![]()
and rating’s dependent pay-off contract
![]()
with expiry![]() . We suppose a solvent risk-free rate of return of
. We suppose a solvent risk-free rate of return of![]() . For simplicity, we will con- sider the following transition matrix
. For simplicity, we will con- sider the following transition matrix
![]()
in which only the default probability ![]() is stochastic.
is stochastic.
For![]() , we have the economy;
, we have the economy;
![]() (5.1a)
(5.1a)
![]() (5.1b)
(5.1b)
![]() (5.1c)
(5.1c)
where
![]()
and
![]()
Letting ![]() and
and![]() , the ultraparabolic Hamilton-Jacobi system of Equations (4.1) for the value function
, the ultraparabolic Hamilton-Jacobi system of Equations (4.1) for the value function ![]() associated with the ultradiffusion (5.1) is then
associated with the ultradiffusion (5.1) is then
![]() (5.2)
(5.2)
for all![]() ,
,
![]() (5.3a)
(5.3a)
for all![]() , such that
, such that
![]() (5.3b)
(5.3b)
for ![]() and
and
![]() (5.3c)
(5.3c)
![]() (5.3d)
(5.3d)
and
![]() (5.4a)
(5.4a)
for all![]() , such that
, such that
![]() (5.4b)
(5.4b)
for ![]() and
and
![]() (5.4c)
(5.4c)
![]() (5.4d)
(5.4d)
Figure 1 and Figure 2 show the value function components ![]() and
and![]() , respectively, for
, respectively, for![]() . Relative to the discretization of (5.2)-(5.4), we utilized
. Relative to the discretization of (5.2)-(5.4), we utilized![]() ,
, ![]() ,
, ![]() ,
,![]() . In particular, we note the effect of the rating based exercise prices on
. In particular, we note the effect of the rating based exercise prices on ![]() and
and ![]() and the de- creasing value of
and the de- creasing value of ![]() with increasing
with increasing![]() , as expected.
, as expected.