The Effective Chiral Model of Quantum Hadrodynamics Applied to Nuclear Matter and Neutron Stars

Hiroshi Uechi

Osaka Gakuin University, Suita, Japan.

DOI: 10.4236/jamp.2015.32017                

Abstract

We review theoretical relations between macroscopic properties of neutron stars and microscopic quantities of nuclear matter, such as consistency of hadronic nuclear models and observed masses of neutron stars. The relativistic hadronic field theory, quantum hadrodynamics (QHD), and mean-field approximations of the theory are applied to saturation properties of symmetric nuclear and neutron matter. The equivalence between mean-field approximations and Hartree approximation is emphasized in terms of renormalized effective masses and effective coupling constants of hadrons. This is important to prove that the direct application of mean-field (Hartree) approximation to nuclear and neutron matter is inadequate to examine physical observables. The equations of state (EOS), binding energies of nuclear matter, self-consistency of nuclear matter, are reviewed, and the result of chiral Hartree-Fock  approximation is shown. Neutron stars and history of nuclear astrophysics, nuclear model and nuclear matter, possibility of hadron and hadron-quark neutron stars are briefly reviewed. The hadronic models are very useful and practical for understanding astrophysical phenomena, nuclear matter and radiation phenomena of nuclei. 

Keywords

A Relativistic Field Theory of Nuclei: Quantum Hadrodynamics (QHD), The Equivalence of Mean-Field Approximations and Hartree Approximation, Density Functional Theory (DFT), Maximum Masses of Neutron Stars

1. Introduction

1.1. Brief History of Supernova and Neutron Stars

A neutron star is a high density object that is anticipated from the gravitational collapse of a massive star during a supernova explosion. Such stars are hypothesized as high density objects mainly composed of neutrons and supported against further collapse because of Pauli exclusion principle exerted by nuclear particles. Hence, the balance between gravitational force and quantum mechanical force produced by nucleons is considered as the reason for stable existence of neutron stars.

The Fermi energy and pressure are produced by nuclear strong interactions, and therefore, properties of astrophysical phenomena and nuclear strong interactions can be directly interconnected.

This is an active research field of nuclear astrophysics. Several relations between many-body system of strongly interacting particles (nuclear matter) and high density matter, such as neutron, hyperon and quark matter are theoretically expected and explained by using relativistic models of nuclear physics [1].

In seeking an explanation for the origin of supernova and high density stars, neutron stars were proposed to be formed in a supernova explosion process (see, Figure 1). Supernovae are suddenly appearing dying stars expected to occur once in 500 - 1000 years in our galaxy, whose luminosity outshines an entire galaxy for days and weeks.

It is proposed that the release of the gravitational binding energy of neutron stars powers the supernova and if the central part of a massive star before its collapse contains about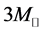, a neutron star of 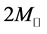can be formed (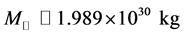: the solar mass). An observed, typical neutron star has a mass from 1.35 to about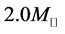, with a radius R ~ 12 km. Theoretical calculations of neutron stars were performed by Tolman, Oppenheimer and Volkoff, and in 1967, a radio pulsar was discovered. Radio pulsars are rapidly rotating with periods in the range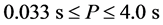. Non-rotating and non-accreting neutron stars were also discussed, whose temperature is expected to be and a radius.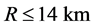

1.2. Observables of Neutron Stars and High Density Equations of State (EOS)

A magnetar is a type of neutron star with an extremely powerful magnetic field, and the emission of copious amounts of high energy electromagnetic radiation is considered as X-rays and gamma rays. The radiation can only be observed when the beam of emission is pointing towards the Earth, which is called the lighthouse effect. The strong magnetic field may have significant effects on both the equation of state (EOS) and the structure of neutron stars.

The magnitude of the magnetic field strength, 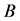, is estimated as,

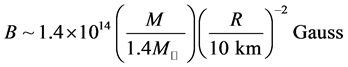(1)

where 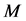and 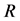are mass and radius of a neutron star. The effect of strong magnetic field on EOS of magnetars is one of the important problems to be investigated. An image and hypothetical structure of a neutron star are shown in Figure 2. The inside of neutron stars is assumed to be composed of hadrons and possibly quarks.

The polytropic equation of state is a useful approximation to consider many cosmological phenomena, because any material will be expected to behave like an ideal gas at a high enough temperature. When the temperature is far enough above the chemical potential or single particle energy of material, its macroscopic behavior is considered well described by a polytropic EOS, for example,

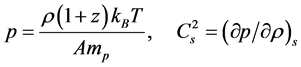(2)

Figure 1. An image of neutron star formation after supernova explosion.

Figure 2. A schematic picture of a magnetized neutron star with magnetic field, B, and the rotation axis Ω.

and

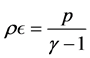(3)

where is the single particle energy (internal energy per particle or internal energy per molecular weight), and and are the Boltzmann constant and temperature, respectively. is the average ionization number; is assumed to be a constant; is the molecular weight (the particle mass divided by 1 amu) and is the proton mass (divided by 1 amu).

The radiation pressure of blackbody and systems in which radiation is important or dominant is expressed as

(4)

where is the temperature; is the speed of light, and is the Stefan-Boltzmann constant familiar from blackbody radiation. Because this pressure depends on T to the fourth power, the radiation pressure will completely dominate at sufficiently high temperature, while material pressures generally depend on T to the first power [2]. It is important to check whether or not it is the case near and inside neutron stars, black holes and within matter during supernova explosions.

The radius and mass of neutron stars are important macroscopic observables. For example, the radiation radius

(5)

is implied from thermal observations of neutron star’s surface. Redshift is defined as

(6)

Moments of inertia, I, the Eddington limit flux from burst sources, and the total neutrino emission released in the gravitational collapse to form a neutron star, etc., are used to check theoretical calculations and consistency of EOSs [3].

The physics of neutron stars offers an interesting interplay between nuclear physics and astrophysical observables. The relevant densities of neutron stars are far from the normal nuclear matter density,. Hence, the determination of EOS for dense matter is essential for calculations of neutron star properties. Nonrelativistic and relativistic many-body approximations, various hadronic models and effective QCD (Quantum Chromodynamics) models are employed to construct EOS of neutron stars. As shown briefly, the EOS determines many properties such as the mass, moments of inertia, mass-radius relation, redshifts, cooling rate, and the total neutrino emission in a supernova explosion.

The relevant degrees of freedom may not be the same in the crust region where the density is much smaller than the saturation density of nuclear matter, and also, hadronic models may be questionable in the center of the star where density is so high. It is essential to study these questions quantitatively by comparing hadronic and QCD equations of state, and discrepancies of predictions or model-independent predictions of both hadronic and quark theories are important in order to understand nuclear physics and sub-nuclear microscopic dynamics.

Within non-relativistic lowest-order Brueckner theory, it suggests that all the new phase-shift equivalent nucleon-nucleon potentials yield essentially similar equations of state up to densities of for both pure neutron matter and -stable matter. Other properties such as symmetry energy and proton fractions show a similar quantitative agreement. The inclusion of complicated many-body terms at the level of two-body interactions does not alter the conclusion [4], which implies that all the non-relativistic many-body approaches mentioned just above give similar equations of state around nuclear matter saturation densities,.

However, the relativistic approaches, three-body interactions, onset of hyperons, pion and kaon condensations, superfluidity, and hadron-quark phase transitions are known to yield significant corrections to EOS above saturation density. In order to obtain consistent results from different approaches, it is essential to examine conditions and constraints to nuclear models and calculations.

2. Nuclear Matter as the Assemblage of Protons and Neutrons

B. D. Serot and J. D. Walecka started applications and analyses of relativistic field theory of nucleons known as quantum hadrodynamics (QHD) [5] [6] to properties of nuclear matter and neutron stars. Since then, so many papers concerning nuclear astrophysics have been published and the field has developed as an active interdisciplinary discipline between nuclear physics and astrophysics.

As one of the extended QHD models, the chiral effective hadronic mean-field approximation (Hartree approximation) and the conserving Dirac-Hartree-Fock approximation are generated. The chiral nonlinear mean-field approximation is an extension of the conserving chiral and nonchiral hadronic mean-field approximation which is a thermodynamically consistent, relativistic and Lorentz-covariant mean-field theory of hadrons [1] [7] [8]. All the masses of hadrons are produced by spontaneous symmetry breaking (SSB) of the following Lagrangian:

(7)

where, and. The chiral symmetry breaking term is given by, and is an infinitesimal parameter.

If coulomb forces were negligible and the number of nucleus was so large that the nucleus was the size of neutron stars, then, mass formula of nucleons becomes simple with binding energies proportional to the number of nucleons. The hypothetical system with equal numbers of protons and neutrons is called nuclear matter (see, Figure 3). If a nuclear model could not produce saturation curve as Figure 3, the model will be rejected. The saturation curve is fundamental to check the theory of nuclear physics.

Figure 3. Nuclear matter is a self-bound system.

The mean-field approximation of (7) and other analogous nonlinear hadronic models are defined by replacing meson quantum fields with classical fields as,

(8)

and pion does not appear directly in the level of mean-field (Hartree) approximation, but the pion contributions appear from HF approximation. The definition of mean-field approximation is equivalent to Hartree approximation [6]-[8].

When J. D. Walecka introduced the mean-field approximation by replacing meson fields with classical fields, it was shown by B. D. Serot [6] that the mean-field approximation is equivalent to Hartree (tadpole diagrams) approximation (see, Figure 4). This fact is important to understand and extend calculations of the mean-field approximations.

3. The Equivalence between Mean-Field Approximations and the Hartree Approximation

Although the QHD calculations have been successful during the last quarter of 20^th century, the original QHD model and approximations to QHD have been extended by including nonlinear interactions of mesons and chiral symmetry (reviews in Chapters 2, 3 and 5, 6 in [1] and references are highly recommended to interested readers).

Nonlinear hadronic models and chiral effective models based on QHD generate nonlinear interaction terms in the form of (the nonlinear parameters, , are expansion coefficients expected to be

much less than 1). The requirement of renormalizability in the level of Lagrangian is abandoned in the effective model of hadrons, but the nonlinear terms are considered as effective interactions in the level of approximations to QHD.

It is shown that nonlinear interactions are interpreted as manifestations of many-body interactions of hadrons and renormalized as effective masses, effective coupling constants and sources of meson equations of motions [8]. This reveals that any mean-field approximations of nonlinear interactions of mesons are equivalent to Hartree approximation when effective masses (see, Figure 5), coupling constants and sources of meson equations of motions are self-consistently renormalized.

Figure 4. The mean-field (Hartree) approximation in terms of tadpole diagrams.

Figure 5. Effective masses of nucleons and mesons in the mean-field approximation of nonlinear chiral Hartree approximation (CHA) [7].

The self-consistency of approximations is essential to prove that all nonlinear approximations with meson interactions are equivalent to the mean-field approximation (Hartree approximation). The requirement of self- consistency is rigorously examined by the functional derivative of energy density, , with respect to density of particles,:

(9)

where is the single particle energy of nucleons. This is consistent with the self-consistent requirement of the theory of conserving approximations [9] and the density functional theory (DFT) [10]. The effective masses and coupling constants are determined to maintain the self-consistency requirement, which become density-de- pendent quantities. Their values are, , , , at nuclear matter saturation density. The nuclear incompressibility and symmetry energy are respectively obtained as, and.

4. The Dirac-Hartree-Fock Approximation as the Basis of the Mean-Field Approximation

The equivalence of the mean-field approximation with the Hartree approximation indicates that the mean-field approximation is not sufficient as the first approximation to nuclear matter. The exchange contributions, Fock terms, should be included, which are as important as the Hartree approximation. Hence, the self-consistent Dirac-Hartree-Fock approximation is sufficient for the first approximation to nuclear matter.

It is important to emphasize that the fundamental requirement (9) is necessary to construct the self-consistent DHF approximation, which is termed as the conserving DHF approximation (CDHF) [11] [12]. The Feynman diagram representation of Hartree-Fock approximation is shown in Figure 6.

One should be careful that the construction of HF approximation as well as other sophisticated approximations by way of Feynman diagram method or the functional derivative method are not necessarily equivalent [8]. The retardation interactions (energy transfers) in interaction processes cause the discrepancy between the Feynman diagram and density functional methods. The self-consistent renormalization of interactions should be carefully defined in an approximation and should be checked by the Equation (9).

The CDHF approximation improves experimental values derived from Hartree (mean-field) approximation, and physical reasons for the improvement can be explained by the binding energy curve at nuclear matter saturation density (Figure 7) and the saturation curves given by Hartree-sector and Fock-sector contributions, respectively (Figure 8).

Figure 6. The Feynman diagram for nucleons and mesons in HF approximation.

Figure 7. Binding energy curves derived from CHA and CHFA. VFC means the vacuum fluctuation corrections.

Figure 8. The contributions to binding energy from Hartree and Fock terms, respectively.

The exchange interactions (Fock contributions) to binding energy are important at low densities compared to Hartree contributions and should not be neglected for nuclear matter calculations.

Therefore, mean-field (Hartree) approximations with nonlinear interactions proposed by other researchers are not sufficient to examine nuclear matter calculations. One can conclude that Hartree-Fock approximation is the correct ground state for nuclear matter calculations.

The equation of state (EOS) derived from the conserving effective CDHF approximation [11] to Lagrangian (7) produces nuclear incompressibility, , and neutron star mass, , as

(10)

where is the solar mass. The CDHF calculation generates reasonable corrections to the mean-field approximation.

The exchange interactions produce attractive interactions at low densities similar to those of Hartree contributions, which render the EOS of Hartree approximation softer around saturation density. The parameters of the effective chiral mean-field model are, and, and they are fixed by conditions of spontaneous symmetry breaking (SSB) and properties at saturation:, and pressure,.

It shows that self-consistency and chiral-symmetry are essentially related to saturation mechanism and confined by physical quantities, such as self-energies, effective masses of baryons and mesons, effective meson- nucleon coupling constants and properties of neutron stars.

In the calculation, nuclear symmetry energy, , is given by

(11)

where is the difference between the proton and neutron density: at a fixed baryon density,. The numerical calculation of requires energy density in

the conserving effective DHF approximation, and MeV in the DHF approximation, which improves the results of the mean-field (Hartree) approximation.

5. Hadron and Hadron-Quark (H-Q) Neutron Stars

The stability criterion for neutron stars is given by the derivative of neutron star mass with respect to central energy: [13], and it is the stability condition for single phase compact stars, such as pure hadronic stars or quark stars (is a central energy density for a neutron star).

The MIT-bag model of QCD is employed to the equation of state for quark-phase calculations. The equation of state generated by MIT-bag model is connected to the hadronic phase (assumed the first-order phase transition) to calculate hadron-quark neutron stars [14].

As hadron-quark (H-Q) stars are 2-phase compact stars (i.e., the quark phase for a star’s core and hadron phase for a mantle), the stability of H-Q stars should be considered carefully. One can see that the quark-core (monotonically increasing dotted line in Figure 9) has a simple positive slope, , with one critical point,.

Hence, the stability criterion, , can be applicable to the quark-core, but may not be applicable to the total mass of the H-Q star. It indicates that a stable quark-core is developing; however, the total mass of H-Q star (a quark-core and a hadron mantle, see Figure 10) shows a decreasing curve (solid line in Figure 9), which may suggest that the hadron mantle would be unstable because of hadron-quark phase transition.

The Figure 9 indicates that stable pure hadronic stars in the central energy range, , will undergo a phase transition (dotted horizontal line), reaching H-Q stars (,is a bag constant of MIT-bag model of nucleons).

The total mass of H-Q stars decreases at high densities (, solid line in Figure 9), but a stable quark-core develops (monotonically increasing dotted line,). The hadron mantle provides the

star-core with quark particles by way of hadron-quark phase transition, resulting in the development of a stable quark-core.

Therefore, the H-Q star is stable in the sense that a stable quark-core is developing, although the total mass of the star decreases. The decreasing mass of hadron-mantle or equivalently the decreasing energy of hadron-man- tle could be used to convert hadrons to produce free quark particles in the deconfined vacuum relative to the confined vacuum, which may be the concept of the bag-constant, , in MIT-bag model.

By comparing stable energy densities of the quark phase with those of H-Q stars, the central energy density of stable H-Q stars is found to be extended at higher densities than that of single phase stars. This suggests that compact stars consisting of a mantle and a high density core are more stable at extremely high densities than stars in a homogeneous single phase structure [15] [16].

When the QCD coupling constant, , increases, the H-Q phase transition density and quark-core will shift to higher densities, but the quark-core is stable and extends to higher densities. If the bag constant is small, such as, one will obtain a saturation curve (an inflection point for stability) within. The appropriate values of and to produce the observed data of neutron stars in the current EOS are related to each other so that if is increased, should be decreased, such as in (,)

Figure 9. Hadron (solid curve) and hadron-quark (dotted-curve) neutron stars.

Figure 10. Imaginary pictures of pure hadron (left) and hadron- quark (right) neutron stars.

and (,). The property of in the analysis of H-Q infinite matter agrees with the results of bag-model fits to light-hadron spectra and renormalization group analyses in the paper by Farhi and Jaffe [16].

Although neutron stars and high density objects have been discussed in a rigorous fashion, they are still in a state of conjecture because of unknown, uncertain observables and parameters of theories and experiments. The interactions of related fields are important for the progress of science and understanding of nuclear astrophysics.

6. Conclusions on the Hadronic Nuclear Mean-Field Theory

The mean-field approximations by replacing meson quantum fields with classical fields in nuclear hadronic models are all equivalent to the Hartree approximation when nonlinear interactions are properly renormalized [17]. It immediately suggests that exchange contributions (Fock interactions) should be included and the Hartree-Fock approximation must be employed as a correct ground state approximation to examine properties of nuclear matter and neutron stars. The contributions from Fock exchange interactions are important to evaluate experimental values of nuclear and neutron stars, and mean-field calculations should be extended.

The hadronic model employed in Section 4 yields reasonable results for properties of nuclear and neutron stars. However, the scalar -meson field is an effective degree of freedom and the lagrangian is considered as an effective nonrenormalizable hadronic model (see, detailed discussions of chapters 2 and 3 in [1]). The mass of scalar -meson is, which is very small compared to -meson masses used by other hadronic models. But, the -meson mass should be considered together with coupling constant in the model. As discussed in [6], when the dimensionless value, , is compared to other models, with gives similar contributions to properties of nuclear matter. The HF approximations should be extended and applicability of effective hadronic models should be investigated further.

The nuclear physics and astrophysics are interrelated on the fundamental level, and hence, discoveries of each field would generate remarkable progresses on theories and technologies for both fields. The knowledge of nuclear physics is important for applications to diverse fields of science. Nuclear energy has been investigated to maintain the energy requirement for our societies. Radioactive materials are very useful for studies and applications of diverse fields. The progress of technologies to control energies is therefore essential, and we have to understand nuclear energies as clearly as possible both in theoretical structures and technological applications in order to control them for the purpose of our societies and environments.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Uechi, H., Uechi, S.T. and Serot, B.D. (2012) Neutron Stars: The Aspect of High Density Matter, Equations of State and Observables. Nova Science Publishers, New York.
[2]	Baym, G. and Pethick, C. (1978) In: Bennemann, K.H. and Ketterson, J.B., Eds., The Physics of Liquid and Solid Helium, Part II, John Wiley, New York.
[3]	Lattimer, J.M. and Prakash, M. (2007) Phys. Rep., 442, 109. http://dx.doi.org/10.1016/j.physrep.2007.02.003
[4]	Heiselberg, H. and Hjorth-Jensen, M. (2000) Phys. Rep., V328, 237. http://dx.doi.org/10.1016/S0370-1573(99)00110-6
[5]	Walecka, J.D. (1974) A Theory of Highly Condensed Matter. Annals of Physics (N.Y.), 83, 491. http://dx.doi.org/10.1016/0003-4916(74)90208-5 Walecka, J.D. (1995) Theoretical Nuclear and Subnuclear Physics. Oxford University Press, New York.
[6]	Serot, B.D. and Walecka, J.D. (1986) Advances in Nuclear Physics, Vol. 16. Negele, J.W. and Vogt, E., Eds., Plenum, New York.
[7]	Uechi, S.T. and Uechi, H. (2009) The Open Nuclear and Particle Physics Journal, V2, 47. Uechi, S.T. and Uechi, H. (2010) arXiv:1003.3630 [nucl-th]. http://arxiv.org/abs/1007.3630
[8]	Uechi, H. (2004) Progress of Theoretical Phys., 111, 525. http://dx.doi.org/10.1143/PTP.111.525
[9]	Baym, G. and Kadanoff, L.P. (1961) Phys. Rev., 124, 287. http://dx.doi.org/10.1103/PhysRev.124.287 Baym, G. (1962) Phys. Rev., 127, 1391. http://dx.doi.org/10.1103/PhysRev.127.1391
[10]	Kohn, W. and Sham, L.J. (1965) Phys. Rev., 140, A1133. Kohn, W. (1999) Rev. Mod. Phys., 71, 1253. http://dx.doi.org/10.1103/RevModPhys.71.1253
[11]	Uechi, H. (2012) The Annual Meeting of Japan Physical Society (JPS), Sept. 26aHB-6.
[12]	Takada, Y. (1995) Phys. Rev., B52, Article ID: 12708.
[13]	Misner, C.W., Thorne, K.S. and Wheeler, J.A. (1973) Gravitation. W. H. Freeman and Company.
[14]	Serot, B.D. and Uechi, H. (1989) Ann. of Phys., 179, 272. http://dx.doi.org/10.1016/0003-4916(87)90137-0 Uechi, S.T. and Uechi, H. (2009) Advances in High Energy Phys., Article ID: 640919. Uechi, S.T. and Uechi, H. (2010) arXiv:1003.4815 [nucl-th]. http://arxiv.org/pdf/1003.4815v1.
[15]	Witten, E. (1984) Phys. Rev., D30, 272. http://dx.doi.org/10.1103/PhysRevD.30.272
[16]	Farhi, E. and Jaffe, R.L. (1984) Phys. Rev., D30, 2379. http://dx.doi.org/10.1103/PhysRevD.30.2379
[17]	Uechi, H. (2006) Nucl. Phys. A, 780, 247. http://dx.doi.org/10.1016/j.nuclphysa.2006.10.015 Uechi, H. (2008) Nucl. Phys. A, 799, 181. http://dx.doi.org/10.1016/j.nuclphysa.2007.11.003