Characteristics Collocation Method of Compressible Miscible Displacement with Dispersion ()
1. Introduction
The mathematical controlling model for compressible miscible displacement in porous media with dispersion is given by
 (1)
(1)
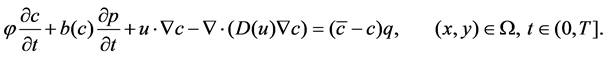 (2)
(2)
where 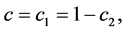
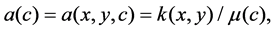
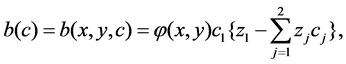
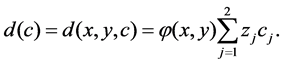
 and
and  denote the concentration and constant compressibility factor for the i component of the fluid mixture respectively. Let
denote the concentration and constant compressibility factor for the i component of the fluid mixture respectively. Let 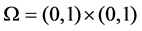 with the boundary
with the boundary ,
, 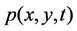 the pressure in the mixture, u is the Darcy velocity of the fluid, and
the pressure in the mixture, u is the Darcy velocity of the fluid, and 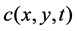 is the relative concentration of the injected fluid.
is the relative concentration of the injected fluid.  and
and 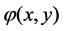 are the permeability and the porosity of porous media,
are the permeability and the porosity of porous media,  is the viscosity of the fluid.
is the viscosity of the fluid. 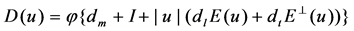 are the molecular dissipation and dispersion terms, where
are the molecular dissipation and dispersion terms, where 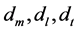 are the molecular dissipation, longitudinal and tangential dispersion coefficients. I is a 2 unit matrix,
are the molecular dissipation, longitudinal and tangential dispersion coefficients. I is a 2 unit matrix, ![]() is a matrix representing orthogonal projection along the velocity vector and
is a matrix representing orthogonal projection along the velocity vector and ![]() is the complementary projection. q and
is the complementary projection. q and ![]() etc. refer to the definition and significance of [1] [2].
etc. refer to the definition and significance of [1] [2].
We shall assume that no flow occurs across the boundary
![]() (3)
(3)
where v is the outer normal to![]() , and the initial conditions are
, and the initial conditions are
![]() (4)
(4)
The compressible flow problems are strongly nonlinear coupling system for partial differential equations of two different types, and we consider the system with dispersion in non-periodic space, so these factors lead to many difficulties for convergence analysis of algorithms. The collocation methods are widely used for solving practice problems in engineering due to its easiness of implementation and high-order accuracy. But the most parts of mathematical theory focused on one-dimensional or two-dimensional constant coefficient problems [3] [4]. [5] proposes the collocation method of two-dimensional variable coefficients elliptic problems. The characteristics collocation scheme for the incompressible flow is given in [6]. The characteristics finite element method for the compressible miscible flow is proved in [7]. In the paper we shall use different technique to treat different types of equations, the orthogonal collocation methods solve the pressure equation and the characteristics collocation scheme approximate the concentration equation. We develop some technique to analyze convergence of these algorithms for this strongly nonlinear system with dispersion in non-periodic space. Finally we can obtain the optimal order error estimate. We shall assume the coefficients ![]()
![]() etc. and their partial derivatives have positive upper and lower bounds independently as well as smoothly. Throughout, the symbols K and
etc. and their partial derivatives have positive upper and lower bounds independently as well as smoothly. Throughout, the symbols K and ![]() will denote, respectively, a generic constant and a generic small positive constant.
will denote, respectively, a generic constant and a generic small positive constant.
The organization of the rest of the paper is as follows. In Section 2, we will present the formulation of the characteristic collocation scheme for nonlinear system (1) (2). In Section 3, we will analyze convergent rate of the scheme defined in Section 2.
2. Characteristic Collocation Scheme (CCS)
2.1. Preliminaries
In this subsection, we will give some basic notations and definition for the characteristics collocation methods, which will be used in this article. We make the partition of the domain![]() , which is quasi-uniform and equally spaced rectangular grid by
, which is quasi-uniform and equally spaced rectangular grid by ![]() and
and ![]() steps along x-direction and y-direction. Let
steps along x-direction and y-direction. Let
![]()
![]()
![]()
![]() .
.
Define function spaces as follows:
![]() ,
,
where ![]() denotes the set of polynomials of degree
denotes the set of polynomials of degree![]() , similarly we can define
, similarly we can define![]() . Let
. Let![]() then let
then let ![]() be the spaces of piecewise Hermite bicubics.
be the spaces of piecewise Hermite bicubics.
Next, we take four Gauss points as collocation points in![]() , and
, and![]() ,
, ![]() , where
, where![]() . Introduce the following summation notation:
. Introduce the following summation notation:
![]()
![]()
Let ![]() be the interpolation operator of piecewise Hermite bicubics on
be the interpolation operator of piecewise Hermite bicubics on![]() , and
, and ![]() and
and ![]() be the interpolation operators of piecewise Hermite bicubics in x and in y, respectively, which may be defined by
be the interpolation operators of piecewise Hermite bicubics in x and in y, respectively, which may be defined by ![]() for sufficiently smooth function v.
for sufficiently smooth function v.
2.2. CCS
In this subsection we will present the fully discrete characteristic collocation scheme for nonlinear system (1) (2) with dispersion term in non-periodic space. At first time ![]() can be discretized:
can be discretized: ![]()
![]() We consider the concentration Equation (2), let
We consider the concentration Equation (2), let![]() , and the characteristic direction associated with the operator
, and the characteristic direction associated with the operator ![]() is denoted by
is denoted by![]() , hence
, hence![]() .
.
The Equation (2) can be put in the form
![]() (5)
(5)
For (5), we use a backward difference quotient for ![]() along the characteristic line:
along the characteristic line:
![]() (6)
(6)
where![]() .
.
So we can obtain the following discrete equation:
![]()
Now that use the interpolation operator ![]() and the Gauss points
and the Gauss points![]() , we give the fully discrete characteristics collocation scheme (CCS):
, we give the fully discrete characteristics collocation scheme (CCS):
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
and ![]() (10)
(10)
for ![]() computed in the order: at first
computed in the order: at first ![]() can be computed from (8), then from (10) and (9) we can solve
can be computed from (8), then from (10) and (9) we can solve![]() . Because the system is non-periodic, we need to do a continuation as shown in Figure 1.
. Because the system is non-periodic, we need to do a continuation as shown in Figure 1.
We can understand the following method intuitively from above schematic diagram. When ![]() is through the boundary
is through the boundary![]() , we will do continuation according to specular reflection method, namely when
, we will do continuation according to specular reflection method, namely when ![]() is outside
is outside![]() , we do the normal from
, we do the normal from ![]() to
to![]() , and the normal intersects
, and the normal intersects ![]() at
at![]() . Then we do inner normal at
. Then we do inner normal at![]() , and we choose point
, and we choose point ![]() so as to
so as to![]() , and the value of
, and the value of ![]() replaces the one of
replaces the one of![]() , in this way c and C etc. functions are certain meaning. Because c satisfies (3), the continuation is logical [7].
, in this way c and C etc. functions are certain meaning. Because c satisfies (3), the continuation is logical [7].
3. Convergence Analysis
In this section we consider the existence and uniqueness of the numerical solution, and obtain the optimal error estimate. CCS (8) (9) can be rewritten as the discrete Galerkin method given by [3] [6] [8]
![]() (11)
(11)
![]() (12)
(12)
We can get the following convergence conclusion for the above numerical Scheme (11) (12).
Theorem 3.1 Suppose![]() , then there exists a constant K such that, for h sufficiently small,
, then there exists a constant K such that, for h sufficiently small,
![]()
Proof: Let ![]() Subtracting (11) from the discrete Galerkin scheme of (1), we obtain the pressure error equation
Subtracting (11) from the discrete Galerkin scheme of (1), we obtain the pressure error equation
![]() (13)
(13)
where![]() , and choosing the test function
, and choosing the test function ![]() in (13), and the right terms can be denoted by
in (13), and the right terms can be denoted by ![]() in turn. For error estimate, we shall need an induction hypothesis. We assume that
in turn. For error estimate, we shall need an induction hypothesis. We assume that
![]() (14)
(14)
We start this induction by seeing that ![]() for h sufficiently small. We shall check that if
for h sufficiently small. We shall check that if![]() , (14) is right at the end of the proof. So we get the error estimate of the pressure [6] [8].
, (14) is right at the end of the proof. So we get the error estimate of the pressure [6] [8].
![]() (15)
(15)
for ![]() sufficiently small.
sufficiently small.
Next we will consider the concentration equation, subtracting (12) from the discrete Galerkin scheme of (2),
![]() (16)
(16)
To obtain optical estimate for ![]() we choose
we choose ![]() as test function in (16), and we denote the resulting right-hand side terms by
as test function in (16), and we denote the resulting right-hand side terms by![]() . And we need another induction hypothesis, we assume that
. And we need another induction hypothesis, we assume that
![]() (17)
(17)
If![]() , we can start the induction by (15) to get
, we can start the induction by (15) to get![]() ,
,
for h sufficiently small and![]() . We shall check that if
. We shall check that if![]() , (17) is right at the end of the proof. Similar to the discussion in [6] [8], and the relations (15) (17) and Gronwall lemma, we can get
, (17) is right at the end of the proof. Similar to the discussion in [6] [8], and the relations (15) (17) and Gronwall lemma, we can get
![]() And it can be combined with (15) to show that
And it can be combined with (15) to show that
![]() .
.
At last we shall check the induction hypotheses (14) and (17)
![]()
for h sufficiently small , and the proof is complete.
Acknowledgements
We thank the fund “Basic Subjects Fund of China University of Petroleum (Beijing) (KYJJ2012-06-04)”.