Introduction
Geometry is equivalent to physics since Einstein has linked gravitation to the geometry of our Universe [1] [2]. The mathematical frame of this geometry is a 4-dimensional manifold where the dimension is this number of real parameters. Nowadays everyone in physics tries to produce a ToE (theory of everything), a theory including gravitation, electromagnetism, weak and strong interactions. String theory, supersymmetry, superstring theory, M-theory, loop quantum gravity, are most famous recent tentatives. This means that the problem is very hard. The aim of this paper is the analysis of these difficulties, preparing new trails to construct such a theory. The basic idea is: perhaps the solution is not so difficult, perhaps we have not be seeking in the right direction. After his discovery of general relativity, Einstein made numerous attempts [3] to get a theory unifying electromagnetism and gravitation. In the same time quantum mechanics was quickly growing, a relativistic wave equation was given by Dirac for the electron. It was then necessary to account not only for gravitation and electromagnetism, but also for the spin 1/2 of the electron and for the quantum wave. Difficulties here begin with the terrible difference between mathematical tools: the 4-dimensional real manifold of the general relativity versus quantum states using hermitical linear spaces over the complex field. Electromagnetism and weak interactions have been partially unified in the Weinberg-Salam model of electro-weak interactions [4], then strong interactions have been described by chromodynamics [5] and both are the main parts of the synthesis known as standard model of quantum physics.
All preceding attempts have supposed that the starting point was necessarily the standard model of quantum physics. The philosophical background of this choice is the believing in the necessity of the theoretical construction made from quantum mechanics. This comes historically from the fact that the first wave equation, found by E. Schrödinger, was able to account not only for one particle, but for a lot of them. Unhappily this wave equation is not relativistic. Consequently it is also unable to account for the spin 1/2, a common property for all fundamental fermions of relativistic quantum physics.
Since 1912 general relativity has made tremendous progress. Solutions were found justifying the behavior of stars with a very strong gravitational field, emitting gravitational waves. Calculations perfectly account for the measurements. On the contrary even if the quantum field theory claims still more precise results, such as the calculation of the Lamb effect or the calculation of the anomalous magnetic moment of the electron, the calculation is difficult: it is a process of successive approximations with the necessity to cut off not a small error but an infinite part of the result: this is not mathematically correct. In fact there are two quantum theories, the first and the second quantification. The first quantification uses for the electron a wave that is a function of space and time with value into the complex field or into a complex vector space. Calculations are exact in the case of the hydrogen atom and results are very precise. The second quantification transforms this wave into something very different, a field of operators operating on something, an object with no mathematical definition. Therefore on the mathematical point of view the departure of the ToE must be the general relativity and neither the second quantification nor any theory using the second quantification.
On the physical point of view it is the same from time properties. Time in physics is not space: in space we can go in any direction, in time we go only from past to future and there is strictly no way to go backwards. Gravitation propagates with gravitational waves that are emitted by stars and the move of these stars is changing with time. All laws of quantum physics are obtained from Lagrangian densities that give the wave equations from a principle of stationarity. This principle was inherited from classical mechanics where the time is not oriented if we forget frictions. Since the true time is the oriented time of thermodynamics, not the time of classical mechanics, only general relativity, allowing the use of an oriented time, is able to be the starting point of the ToE. General relativity and standard model are both obtained from a principle of stationarity, this is certainly another cornerstone to build the ToE (private discussion with D. Girardot).
1. Clifford Algebra of the 3-Dimensional Space
Clifford algebras on the real field are a necessary tool because particles with spin 1/2 exist. We use here all notations of “New insights in the standard model of quantum physics in Clifford Algebra” [6]. Its first chapter study at an elementary level the three Clifford algebras used in the present work. The algebra 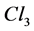 of the physical space is sufficient to describe the physical space-time because
of the physical space is sufficient to describe the physical space-time because
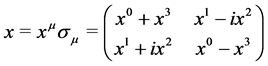 (1.1)
(1.1)
forms the auto-adjoint subspace of the Clifford algebra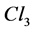 . The wave of an electron is a function of this part of
. The wave of an electron is a function of this part of 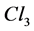 into the full algebra:
into the full algebra: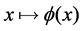 . The Dirac wave equation reads in this frame
. The Dirac wave equation reads in this frame
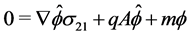 (1.2)
(1.2)
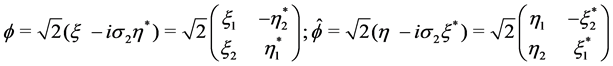
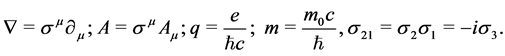 (1.3)
(1.3)
where 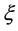 and
and 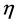 are respectively right and left Weyl spinors,
are respectively right and left Weyl spinors, 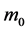 is the proper mass and
is the proper mass and 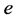 is the negative charge of the electron1. The Dirac equation is the linear approximation of our non-linear homogeneous wave equation
is the negative charge of the electron1. The Dirac equation is the linear approximation of our non-linear homogeneous wave equation
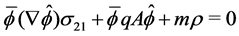 (1.4)
(1.4)
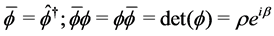 (1.5)
(1.5)
where ![]() is the Yvon-Takabayasi angle. The non-linear wave equation has the Dirac equation as linear approximation if this angle is null or very small.
is the Yvon-Takabayasi angle. The non-linear wave equation has the Dirac equation as linear approximation if this angle is null or very small.
I recall now how the wave equation is said form invariant: If ![]() is any element in
is any element in ![]() and if
and if ![]() is the transformation from the space-time into itself, which to any
is the transformation from the space-time into itself, which to any ![]() associates
associates ![]() such as
such as
![]() (1.6)
(1.6)
we note, if![]() :
:
![]() (1.7)
(1.7)
We then get:
![]()
![]()
![]() (1.8)
(1.8)
![]() multiplies then by
multiplies then by ![]() any space-time distance and is called “Lorentz dilation with ratio
any space-time distance and is called “Lorentz dilation with ratio![]() ”. If we let, with the usual convention summing the up and down indices:
”. If we let, with the usual convention summing the up and down indices:
![]() (1.9)
(1.9)
we get for![]() :
:
![]() (1.10)
(1.10)
![]() has then the same sign as
has then the same sign as ![]() at the origin:
at the origin: ![]() conserves the arrow of the time. Even more we get (the calculation is in [7] A.2.1 and A.2.4):
conserves the arrow of the time. Even more we get (the calculation is in [7] A.2.1 and A.2.4):
![]() (1.11)
(1.11)
![]() (1.12)
(1.12)
![]() conserves therefore the orientation of space-time and as it conserves the time orientation it conserves also the space orientation. Relativistic quantum mechanics lets
conserves therefore the orientation of space-time and as it conserves the time orientation it conserves also the space orientation. Relativistic quantum mechanics lets
![]() (1.13)
(1.13)
and non relativistic quantum mechanics uses the same relation with ![]() only in
only in![]() . All properties of par-
. All properties of par-
ticles with spin ![]() such as Clebsch-Gordon coefficients are deduced from (1.13) and from the properties of the
such as Clebsch-Gordon coefficients are deduced from (1.13) and from the properties of the
matrix representations of![]() . The wave Equation (1.4) is form invariant because
. The wave Equation (1.4) is form invariant because
![]() (1.14)
(1.14)
![]() (1.15)
(1.15)
![]() (1.16)
(1.16)
Here (1.14) comes from (1.11) and (1.13). The relation (1.15) is necessary to get the gauge invariance of the electromagnetism and comes from
![]() (1.17)
(1.17)
The relation (1.16) comes from (1.5), (1.7), (1.13) that give
![]() (1.18)
(1.18)
and (1.16) is then equivalent to
![]() (1.19)
(1.19)
The set ![]() of the
of the ![]() matrices is a 8-dimensional real Lie group. The application
matrices is a 8-dimensional real Lie group. The application ![]() is an homomorphism of
is an homomorphism of ![]() into the 7-dimensional Lie group
into the 7-dimensional Lie group ![]() of Lorentz dilations, each dilation being the product, in any order, of an element of the restricted Lorentz group
of Lorentz dilations, each dilation being the product, in any order, of an element of the restricted Lorentz group ![]() and of a homothety with ratio
and of a homothety with ratio![]() . The kernel of this homomorphism is 1-dimensional, it is the
. The kernel of this homomorphism is 1-dimensional, it is the ![]() set of the
set of the ![]() where
where ![]() gives the orientation of the physical space. We consider the
gives the orientation of the physical space. We consider the ![]() group as the true group of invariance of the Dirac wave and of the electromagnetism2 [6]-[8]. This group is greater than the
group as the true group of invariance of the Dirac wave and of the electromagnetism2 [6]-[8]. This group is greater than the ![]() group of relativistic quantum mechanics, then there are less invariant terms: now
group of relativistic quantum mechanics, then there are less invariant terms: now ![]() and
and ![]() are not separately invariant, (1.16) means that only the
are not separately invariant, (1.16) means that only the ![]() product remains invariant under
product remains invariant under![]() .
.
Our wave equation is gauge invariant under two gauges. The first one is well known since it is the electric gauge
![]() (1.20)
(1.20)
The second one is only a global gauge, it is the chiral gauge
![]() (1.21)
(1.21)
Each gauge is linked to a conserved current. The current linked to the electric gauge is the current of probability
![]() (1.22)
(1.22)
The second conserved current is the ![]() current satisfying
current satisfying
![]() (1.23)
(1.23)
Components ![]() and
and ![]() of these space-time vectors are 8 of the 36 components of tensorial densities available from the 8 real parameters of the wave of the electron (the Dirac theory knows only 16 of them). At each point
of these space-time vectors are 8 of the 36 components of tensorial densities available from the 8 real parameters of the wave of the electron (the Dirac theory knows only 16 of them). At each point ![]() the value of the wave
the value of the wave ![]() has exactly the same form as the
has exactly the same form as the ![]() matrix, then we can associate to this value the geometric transformation
matrix, then we can associate to this value the geometric transformation![]() , with ratio
, with ratio![]() :
:
![]() (1.24)
(1.24)
And the components ![]() of the four
of the four ![]() are the 16 terms of the matrix of the dilation because
are the 16 terms of the matrix of the dilation because
![]() (1.25)
(1.25)
There is no difference between the matrix product ![]() which gives the composition of dilations
which gives the composition of dilations ![]() and the product
and the product ![]() which gives the transformation of the wave under a dilation, and this induces then a composition of dilations
which gives the transformation of the wave under a dilation, and this induces then a composition of dilations![]() :
:
![]() (1.26)
(1.26)
This means that the ![]() introduced into (1.24) does not change, either seen by the observer of
introduced into (1.24) does not change, either seen by the observer of ![]() or by the observer of
or by the observer of![]() . It is independent on the observer, intrinsic to the wave.
. It is independent on the observer, intrinsic to the wave.
And since ![]() is function of
is function of![]() , the dilation is also a function of
, the dilation is also a function of![]() , and varies from a point to another in space-time:
, and varies from a point to another in space-time: ![]() is not an element of the global space-time, only of the local space-time. So we must see
is not an element of the global space-time, only of the local space-time. So we must see ![]() as the general element of the tangent space-time, at
as the general element of the tangent space-time, at![]() , to a space-time manifold which depends only on the wave, not on the observer, and that we will name “intrinsic manifold”. On the contrary the dilation depends on the observer, the observer of
, to a space-time manifold which depends only on the wave, not on the observer, and that we will name “intrinsic manifold”. On the contrary the dilation depends on the observer, the observer of ![]() sees
sees![]() , the one of
, the one of ![]() sees
sees![]() .
.
The geometric meaning of the Dirac wave is as follows: At each point of the space-time we have, not only one space-time manifold, but two space-time manifolds: the manifold of the ![]() and
and![]() , for which each relativistic observer is associated to a Lorentzian tangent space-time, and the intrinsic manifold, this of the
, for which each relativistic observer is associated to a Lorentzian tangent space-time, and the intrinsic manifold, this of the ![]() which is a manifold with torsion [7] [8]. Moreover each tangent space-time has an orthonormal basis allowing to construct a Clifford algebra. The fiber of each of these two manifolds is then a same Clifford algebra.
which is a manifold with torsion [7] [8]. Moreover each tangent space-time has an orthonormal basis allowing to construct a Clifford algebra. The fiber of each of these two manifolds is then a same Clifford algebra.
2. Wave of Electron + Neutrino in Cl1,3
The electric gauge is the reason of the electric interaction of the electron. Similarly the second gauge of the electron is linked to the weak interaction of the electron. The Weinberg-Salam model of electro-weak interactions [4] considers the right ![]() and left
and left ![]() waves of the electron and the left wave
waves of the electron and the left wave ![]() of the electronic neutrino. If a right
of the electronic neutrino. If a right ![]() wave exists it does not interact neither electrically nor weakly. Therefore the standard model supposes
wave exists it does not interact neither electrically nor weakly. Therefore the standard model supposes![]() .
.
Relativistic quantum mechanics supposes also a link between the wave of the particle and the wave of its anti-particle. Noting now ![]() the wave of the electron, this link reads in space algebra (see [6] 2.4.2)
the wave of the electron, this link reads in space algebra (see [6] 2.4.2)
![]() (2.1)
(2.1)
Then the wave of electron + positron + neutrino + antineutrino is a function of ![]() with value in a 12-dimen- sional subspace of
with value in a 12-dimen- sional subspace of![]() . The form invariance of the wave implies that
. The form invariance of the wave implies that ![]() and
and ![]() must transform similarly. The lepton wave
must transform similarly. The lepton wave ![]() is a function of
is a function of ![]() into the Clifford algebra of space-time
into the Clifford algebra of space-time ![]() [9]:
[9]:
![]() (2.2)
(2.2)
![]() (2.3)
(2.3)
![]() (2.4)
(2.4)
The link between ![]() and
and ![]() is made by the Pauli matrices
is made by the Pauli matrices ![]() and the matrix representation3
and the matrix representation3
![]() (2.5)
(2.5)
With this matrix representation the reverse of ![]() is
is
![]() (2.6)
(2.6)
The invariant form of the wave equation of electron + neutrino reads [10]
![]() (2.7)
(2.7)
where we have to define![]() ,
, ![]() and
and![]() . The covariant derivative
. The covariant derivative ![]() satisfies
satisfies
![]() (2.8)
(2.8)
![]() (2.9)
(2.9)
The ![]() are four operators so defined:
are four operators so defined:
![]() (2.10)
(2.10)
![]() (2.11)
(2.11)
![]() (2.12)
(2.12)
![]() (2.13)
(2.13)
![]() (2.14)
(2.14)
The ![]() term generalizes the
term generalizes the ![]() of the electron:
of the electron:
![]() (2.15)
(2.15)
![]() (2.16)
(2.16)
![]() (2.17)
(2.17)
![]() (2.18)
(2.18)
and ![]() satisfies
satisfies
![]() (2.19)
(2.19)
![]() (2.20)
(2.20)
The invariant wave Equation (2.7) has a real scalar part [10] that is simply
![]() (2.21)
(2.21)
where ![]() is the Lagrangian density that gives the whole Equation (2.7) by Lagrange equations. Another of the real equations equivalent to (2.7) is
is the Lagrangian density that gives the whole Equation (2.7) by Lagrange equations. Another of the real equations equivalent to (2.7) is
![]() (2.22)
(2.22)
Then there is only one conservative current, it is the sum of the current of the electron and the same current for the neutrino. The wave equation is gauge invariant [10] under the ![]() gauge group generated by operators
gauge group generated by operators![]() . The wave equation is form invariant under the dilation
. The wave equation is form invariant under the dilation ![]() generated by any
generated by any ![]() matrix satisfying (1.6), because, if
matrix satisfying (1.6), because, if
![]() (2.23)
(2.23)
![]() is a group isomorphism, the transformation of the wave satisfies
is a group isomorphism, the transformation of the wave satisfies
![]() (2.24)
(2.24)
which gives, with (1.19)
![]() (2.25)
(2.25)
In the space-time algebra we use
![]() (2.26)
(2.26)
We note ![]() the n-vector part of the multivector
the n-vector part of the multivector![]() . The geometric transformation
. The geometric transformation ![]() in (1.24) linked to the wave reads now
in (1.24) linked to the wave reads now
![]() (2.27)
(2.27)
Similarly to the electron case ![]() is independent from the observer, intrinsic to the wave since under the dilation
is independent from the observer, intrinsic to the wave since under the dilation ![]() we get
we get
![]() (2.28)
(2.28)
![]() (2.29)
(2.29)
Relation (2.27) is equivalent to
![]() (2.30)
(2.30)
![]() (2.31)
(2.31)
Then D is an affine transformation where indices 1 and 2 play a very different role. This is evidently linked to the fact that ![]() is present in the wave equation of the electron and
is present in the wave equation of the electron and ![]() is present in the wave of the electron + neutrino. This anisotropy is the reason of the existence of three kinds of leptons.
is present in the wave of the electron + neutrino. This anisotropy is the reason of the existence of three kinds of leptons.
We know three generations of leptons and quarks and the standard model study separately these three generations. The reason is simply that our physical space is three dimensional, and we get the wave equation of leptons three times. One of the three is (2.7) that reads:
![]() (2.32)
(2.32)
![]() (2.33)
(2.33)
![]() (2.34)
(2.34)
To go from one generation to another one is simple: we permute indices 1, 2, 3 of ![]() everywhere in all preceding formulas with the circular permutation
everywhere in all preceding formulas with the circular permutation ![]() or
or![]() :
:
![]() (2.35)
(2.35)
We do not know if the muon is obtained by ![]() or by
or by![]() . If it is
. If it is![]() , the wave of the pair muon-muonic neutrino follows (2.33) and this explains why a muon is like an electron, generally. But the covariant derivative is different, because in the place of (2.10) to (2.14) we must use
, the wave of the pair muon-muonic neutrino follows (2.33) and this explains why a muon is like an electron, generally. But the covariant derivative is different, because in the place of (2.10) to (2.14) we must use
![]() (2.36)
(2.36)
![]() (2.37)
(2.37)
![]() (2.38)
(2.38)
![]() (2.39)
(2.39)
![]() (2.40)
(2.40)
We must also change the link (2.1) between the wave of the particle and the wave of the antiparticle, link using a ![]() for the first generation. The wave of the anti-muon must satisfy:
for the first generation. The wave of the anti-muon must satisfy:
![]() (2.41)
(2.41)
and we shall have a 3 index in the case of the last generation. We must also change the definition of left and right wave. For the second generation this becomes
![]() (2.42)
(2.42)
and me must also permute the indexes in the geometric transformation (2.31). We can then understand why the Lagrangian density, which comes from the scalar part of the invariant equation, must be calculated separately for the pair electron-electronic neutrino and for the pair muon-muonic neutrino or tau-tauic neutrino.
If there are only three objects like![]() , there is one other term with square −1 in
, there is one other term with square −1 in![]() ,
,![]() . this fourth term allows a fourth neutrino [11].
. this fourth term allows a fourth neutrino [11].
3. Standard Model in Cl1,5
The standard model adds to the leptons (electron and its neutrino) in the first “generation” two quarks ![]() and
and ![]() with three states each. Weak interactions acting only on left waves of quarks (and right waves of antiquarks) the wave of all fermions of the first generation satisfies:
with three states each. Weak interactions acting only on left waves of quarks (and right waves of antiquarks) the wave of all fermions of the first generation satisfies:
![]() (3.1)
(3.1)
![]() (3.2)
(3.2)
![]() (3.3)
(3.3)
The ![]() wave is now a function of space and time with value into
wave is now a function of space and time with value into ![]() which is a sub-algebra (on the real field) of
which is a sub-algebra (on the real field) of ![]() 4. The covariant derivative (2.8) becomes
4. The covariant derivative (2.8) becomes
![]() (3.4)
(3.4)
![]() (3.5)
(3.5)
![]() (3.6)
(3.6)
![]() (3.7)
(3.7)
![]() (3.8)
(3.8)
We use two projectors satisfying
![]() (3.9)
(3.9)
Three operators act on quarks like on leptons:
![]() (3.10)
(3.10)
![]() (3.11)
(3.11)
The fourth operator acts differently on the lepton and on the quark sector:
![]() (3.12)
(3.12)
![]() (3.13)
(3.13)
These definitions are absolutely all that you have to change to go from the lepton case into the quark case, to get the gauge group of electro-weak interactions. We proved in [6] 6.3 that this gives:
![]() (3.14)
(3.14)
![]() (3.15)
(3.15)
![]() (3.16)
(3.16)
![]() (3.17)
(3.17)
This means that changing the coefficient 1 of ![]() into
into ![]() is sufficient to get the correct charges of
is sufficient to get the correct charges of ![]() and
and ![]() quarks, the correct charges of antiquarks
quarks, the correct charges of antiquarks ![]() and
and![]() . Moreover we get a doublet of left waves for the quarks and a doublet of right waves for the antiquarks:
. Moreover we get a doublet of left waves for the quarks and a doublet of right waves for the antiquarks:
![]() (3.18)
(3.18)
which gives
![]() (3.19)
(3.19)
![]() (3.20)
(3.20)
![]() (3.21)
(3.21)
Then all features of electro-weak interactions of leptons and quarks are simply obtained from the structure of the wave, itself linked to the structure of the space-time
The generators of the ![]() gauge group of chromodynamics use two projectors:
gauge group of chromodynamics use two projectors:
![]() (3.22)
(3.22)
and eight operators![]() ,
, ![]() so defined (with
so defined (with ![]() instead
instead![]() ):
):
![]() (3.23)
(3.23)
![]() (3.24)
(3.24)
![]() (3.25)
(3.25)
![]() (3.26)
(3.26)
![]() (3.27)
(3.27)
![]() (3.28)
(3.28)
We explained in [9] how these operators are equivalent to the eight generators ![]() of
of![]() . Everywhere in (3.23) to (3.28) the eight matrices
. Everywhere in (3.23) to (3.28) the eight matrices ![]() have a zero left up term, therefore all
have a zero left up term, therefore all ![]() project the wave on its quark sector. The physical translation is: leptons do not interact by strong interactions, this comes from the structure itself of the quantum wave. We consider this result as a great success of real Clifford algebras. Now with
project the wave on its quark sector. The physical translation is: leptons do not interact by strong interactions, this comes from the structure itself of the quantum wave. We consider this result as a great success of real Clifford algebras. Now with
![]()
![]() (3.29)
(3.29)
where the eight ![]() are part of what is named “gluons”, the covariant derivative reads
are part of what is named “gluons”, the covariant derivative reads
![]() (3.30)
(3.30)
The gauge group is obtained by exponentiation. We use four numbers ![]() and eight numbers
and eight numbers![]() . We let
. We let
![]() (3.31)
(3.31)
![]() (3.32)
(3.32)
We get
![]() (3.33)
(3.33)
in any order, because:
![]() (3.34)
(3.34)
![]() (3.35)
(3.35)
Therefore the set
![]() (3.36)
(3.36)
is a ![]() Lie group. The gauge transformation reads
Lie group. The gauge transformation reads
![]() (3.37)
(3.37)
![]() (3.38)
(3.38)
![]() (3.39)
(3.39)
![]() (3.40)
(3.40)
![]() (3.41)
(3.41)
The ![]() group of
group of ![]() operators, generated by projectors on the quark sector, acts only on this sector of the wave:
operators, generated by projectors on the quark sector, acts only on this sector of the wave:
![]() (3.42)
(3.42)
We then get the gauge group of the standard model, automatically, and not another group. It is impossible to get operators exchanging ![]() and
and ![]() like
like ![]() exchanging
exchanging ![]() and
and ![]() because
because ![]() is 12-dimensional on
is 12-dimensional on ![]() while
while ![]() is 8-dimensional on
is 8-dimensional on![]() . Then we cannot get a greater group than the preceding
. Then we cannot get a greater group than the preceding ![]() gauge group. This limitation is linked to the geometric structure of the wave. The physical consequence is the experimental fact that the proton cannot disintegrate. This is said in the language of quantum field theory by saying that the baryonic quantum number is conservative.
gauge group. This limitation is linked to the geometric structure of the wave. The physical consequence is the experimental fact that the proton cannot disintegrate. This is said in the language of quantum field theory by saying that the baryonic quantum number is conservative.
We have still supposed nothing on![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() . But the standard model uses only left waves for the particles in the case of electro-weak interactions (and right waves for the antiparticles). Why ? I think possible to give a mathematical reason to this physical hypothesis. If
. But the standard model uses only left waves for the particles in the case of electro-weak interactions (and right waves for the antiparticles). Why ? I think possible to give a mathematical reason to this physical hypothesis. If ![]() and
and ![]() quarks have only left wave, this means
quarks have only left wave, this means ![]() waves, we have:
waves, we have:
![]() (3.43)
(3.43)
and two similar equalities for colors g and b. Now we define two matrices ![]() and
and![]() :
:
![]() (3.44)
(3.44)
and we got the remarkable identity [6]
![]() (3.45)
(3.45)
Usually ![]() therefore
therefore ![]() is invertible. We can see the wave
is invertible. We can see the wave![]() , which implies by its structure itself the gauge group of the standard model, as having the maximum number (36) of degrees of freedom compatible with the existence of an inverse wave. And we need the existence of the inverse to allow the construction of the wave of systems of fermions (See [12] and [9] 4.4.1).
, which implies by its structure itself the gauge group of the standard model, as having the maximum number (36) of degrees of freedom compatible with the existence of an inverse wave. And we need the existence of the inverse to allow the construction of the wave of systems of fermions (See [12] and [9] 4.4.1).
To add two quarks with three colors each in the second and in the third generation we need
![]() (3.46)
(3.46)
and two similar definitions for colors g and b. Now since the ![]() generators of the
generators of the ![]() group of chromodynamics are unchanged by the circular permutation
group of chromodynamics are unchanged by the circular permutation ![]() used to pass from one generation to another, strong interactions are unperturbed by the change of generation. This allows physical quarks composing particles to mix the generations. For instance the physical quark
used to pass from one generation to another, strong interactions are unperturbed by the change of generation. This allows physical quarks composing particles to mix the generations. For instance the physical quark ![]() present in protons and neutrons is thought as a mixing of the d of the first generation and the s that is the equivalent of d in the second generation. Even if the wave of an antiquark is linked to the wave of the corresponding quark, the mixing of waves of different generations, and the difference between what we call “left” and “right” part in each generation, induce the wave of physical quarks to have both a left and a right wave.
present in protons and neutrons is thought as a mixing of the d of the first generation and the s that is the equivalent of d in the second generation. Even if the wave of an antiquark is linked to the wave of the corresponding quark, the mixing of waves of different generations, and the difference between what we call “left” and “right” part in each generation, induce the wave of physical quarks to have both a left and a right wave.
The link between the reverse in ![]() and the reverse in
and the reverse in ![]() is not trivial and is similar to ([6] A.2). This link reads
is not trivial and is similar to ([6] A.2). This link reads
![]() (3.47)
(3.47)
This link does not exist in ![]() nor in
nor in![]() . We can see the link as a consequence both of the one-dimensionality of the time and of (2.1) that reduces the dimension of the Clifford algebra. It has then also a geometric meaning. If this link (2.1) between the wave of the particle and the wave of the antiparticle is not used we need one dimension more, we loose the link between the different kinds of reverse, then we loose the geometric transformation linked to the wave. We have then good reasons to think that
. We can see the link as a consequence both of the one-dimensionality of the time and of (2.1) that reduces the dimension of the Clifford algebra. It has then also a geometric meaning. If this link (2.1) between the wave of the particle and the wave of the antiparticle is not used we need one dimension more, we loose the link between the different kinds of reverse, then we loose the geometric transformation linked to the wave. We have then good reasons to think that ![]() is the true frame necessary and sufficient to get the gauge group required by experimental results. And this is so more interesting than we can consider the space-time manifold with signature + - - - as embedded in a space-time manifold with signature + - - - - -. The wave equation for all objects of the first generation reads [13]
is the true frame necessary and sufficient to get the gauge group required by experimental results. And this is so more interesting than we can consider the space-time manifold with signature + - - - as embedded in a space-time manifold with signature + - - - - -. The wave equation for all objects of the first generation reads [13]
![]() (3.48)
(3.48)
where we use the scalar densities ![]() and
and ![]() terms satisfying
terms satisfying
![]() (3.49)
(3.49)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (3.50)
(3.50)
We use
![]() (3.51)
(3.51)
![]() (3.52)
(3.52)
![]() (3.53)
(3.53)
The wave Equation (3.48) is gauge invariant under the gauge transformation (3.37) to (3.41) [13]. It is form invariant under the transformation ![]() in (1.6) because with
in (1.6) because with
![]() (3.54)
(3.54)
we get [13]
![]() (3.55)
(3.55)
From (3.54) which is equivalent to
![]() (3.56)
(3.56)
and from the link ![]() between the wave of the particle and the wave of the antiparticle (3.54) is equivalent to
between the wave of the particle and the wave of the antiparticle (3.54) is equivalent to
![]() (3.57)
(3.57)
for any index![]() . It happens that
. It happens that ![]() because the n-vectors of
because the n-vectors of ![]() are the (6-n)-vectors of
are the (6-n)-vectors of![]() . The natural generalization of
. The natural generalization of ![]() uses vectors and pseudovectors of
uses vectors and pseudovectors of![]() . Noting with a 5 index all terms that are components of 5-vectors we let
. Noting with a 5 index all terms that are components of 5-vectors we let
![]() (3.58)
(3.58)
![]() (3.59)
(3.59)
![]() (3.60)
(3.60)
And since we can separate the different multivector parts, (3.60) is equivalent to the system:
![]() (3.61)
(3.61)
![]() (3.62)
(3.62)
![]() (3.63)
(3.63)
![]() (3.64)
(3.64)
With (1.7) (3.63) and (3.64) read
![]() (3.65)
(3.65)
![]() (3.66)
(3.66)
This separation between the different components of the global space-time explains why we usually see only the real components of the 4-dimensional space-time vector![]() . Only the usual space-time has real components. Relations (3.65) and (3.66) indicates both that these two supplementary real dimensions give one complex dimension and that they separate completely the usual space-time in the global space-time. A space-time with one or two supplementary conditions has been used early [3]. The problem was always to explain why classical physics do not see these supplementary dimensions. Here this problem is automatically solved by the difference coming from the invariance group of physical laws.
. Only the usual space-time has real components. Relations (3.65) and (3.66) indicates both that these two supplementary real dimensions give one complex dimension and that they separate completely the usual space-time in the global space-time. A space-time with one or two supplementary conditions has been used early [3]. The problem was always to explain why classical physics do not see these supplementary dimensions. Here this problem is automatically solved by the difference coming from the invariance group of physical laws.
The link (3.49) between the reversion into ![]() and the reversion into
and the reversion into ![]() allows to extend the transformation linked to the wave. We let
allows to extend the transformation linked to the wave. We let
![]() (3.67)
(3.67)
![]() (3.68)
(3.68)
![]() (3.69)
(3.69)
The transformation linked to the wave reads
![]() (3.70)
(3.70)
![]() (3.71)
(3.71)
Similarly to what we said from (1.26), ![]() is independent on the observer, intrinsic to the wave. Contrarily to the dilation
is independent on the observer, intrinsic to the wave. Contrarily to the dilation ![]() where the real space-time is well separated with (3.61), the transformation (3.70) is a transformation from the subspace of the
where the real space-time is well separated with (3.61), the transformation (3.70) is a transformation from the subspace of the ![]() into the same subspace of the relative manifold. We get from (3.1), (3.47) and (3.70)
into the same subspace of the relative manifold. We get from (3.1), (3.47) and (3.70)
![]() (3.72)
(3.72)
![]() (3.73)
(3.73)
![]() (3.74)
(3.74)
Next we let
![]() (3.75)
(3.75)
![]() (3.76)
(3.76)
![]() (3.77)
(3.77)
![]() (3.78)
(3.78)
and we get
![]() (3.79)
(3.79)
We consider now the geometric transformation![]() . It is much more complicated than (2.30), because it is not possible to separate 1-vector and 5-vector. This comes from the identity between
. It is much more complicated than (2.30), because it is not possible to separate 1-vector and 5-vector. This comes from the identity between ![]() and
and![]() . The
. The ![]() transformation applies the linear space
transformation applies the linear space ![]() onto
onto![]() .
.
4. Concluding Remarks
A quantum wave equation generalizing the Dirac wave equation has been proposed to explain the experimental results of the standard model of quantum physics. It does not require the second quantification nor the very tedious calculations brought by its method of approximation. The wave is a true function of space and time with value into well-defined Clifford algebras. It will then be easier to bring together this frame and the solid similar frame of general relativity.
It is very important to notice that these two frames use a same time. This time is our oriented time and the invariance group of the wave conserves this orientation. When the variational calculus is used to go from a Lagrangian density to the corresponding wave equations an integration by parts is necessary, and the assumption that it is possible to cancel solutions at infinity. This hypothesis seems physically equivalent to suppress the propagation. The result is that quantum fields theory is fully satisfactory for stationary states but is structurally unable to account for any irreversible process. Our study explains why Lagrangian densities take place everywhere in quantum physics: they are only the scalar part of the invariant wave equations of fermions. They are not at all fundamental, they are only a mathematical tool.
Fermions are useful and fundamental, but our Universe has not only fermions but also boson waves. We suspect that the boson part of our universe, that contains the massless photon, does not come from a Lagrangian density. For instance the theory of the photon made by L. de Broglie [14] [15] gives not one, but two Lagrangian densities. This is normal since his photon comes from two Dirac waves, and each one brings its own Lagrangian density.
Another important point is emphasized by T. Socroun [16]: in order to get the unification between gravitation and electromagnetism, it is necessary to incorporate charges into potentials terms. This is equivalent, in fact, to the prescription made by Einstein itself that all laws of physics are covariant. With ![]() as fundamental group of invariance the difference between contravariant and covariant terms is a physical one: a contravariant vector in space-time transforms as
as fundamental group of invariance the difference between contravariant and covariant terms is a physical one: a contravariant vector in space-time transforms as ![]() in (1.6) while a covariant vector transforms as
in (1.6) while a covariant vector transforms as ![]() in (1.11). These two transformations are not equivalent as soon as
in (1.11). These two transformations are not equivalent as soon as![]() . It is easy to see that the incorporation of the charges
. It is easy to see that the incorporation of the charges![]() ,
, ![]() ,
, ![]() into the potentials can be made inside each of our preceding equations. The electromagnetic potential gives instead (1.2), (1.3) and (1.15)
into the potentials can be made inside each of our preceding equations. The electromagnetic potential gives instead (1.2), (1.3) and (1.15)
![]() (4.1)
(4.1)
So the three charges disappear in the calculations. For electro-weak interactions and strong interactions we let
![]() (4.2)
(4.2)
Then the covariant derivative (3.4) is simply
![]() (4.3)
(4.3)
Why this has never been made? The reason is probably that theories of great unification consider the charges as slowly variable with the scale of energy and hope that when these charges become equal the structure of the gauge group is enlarged. This is strictly impossible when charges are integrated into potential terms. But this is a new scope as soon as we have linked the generators of the gauge group to the structure of the wave in (2.37) to (2.40), (3.10) to (3.13), (3.23) to (3.28). Since all attempts made to get the unification have failed, the incorporation of charges into potentials is a cornerstone for the ToE. To get the ToE perhaps will it be sufficient to link the Lagrangian density of the general relativity to the Lagrangian density coming from the standard model? (D. Girardot, private discussion) This density is the real scalar part of the invariant wave Equation (3.48)
![]() (4.4)
(4.4)
This density is easily generalized to three generations of fundamental fermions:
![]() (4.5)
(4.5)
It is indeed very sophisticated but on the mathematical point of view it is not so different from the Lagrangian density of general relativity, they are both real functions of space and time.
Another cornerstone of a future ToE is the fact that both theories use a covariant derivative. We must understand how these two covariant derivative coexists. A simple hypothesis coming from the double manifold encountered in (1.24) is that each one can be the covariant derivative on one of the two manifolds. Is one of these two manifolds simply embedded into the other?