Robust Optimization for a Multi-Product Integrated Problem of Planning and Scheduling under Products Uncertainty

Mengwen Chen^*, Cuiwen Cao

Key Laboratory of Advanced Control and Optimization for Chemical Processes, Ministry of Education, East China University of Science and Technology, Shanghai, China.

DOI: 10.4236/jamp.2015.31003                

Abstract

This paper presents robust optimization models for a multi-product integrated problem of planning and scheduling (based on the work of Terrazas-Moreno & Grossmann (2011) [1]) under products prices uncertainty. With the objective of maximizing the total profit in planning time horizon, the planning section determines the amount of each product, each product distributed to each market, and the inventory level in each manufacturing site during each scheduling time period; the scheduling section determines the products sequence, start and end time of each product running in each production site during each scheduling time period. The uncertainty sets used in robust optimization model are box set, ellipsoidal set, polyhedral set, combined box and ellipsoidal set, combined box and polyhedral set, combined box, ellipsoidal and polyhedral set. The genetic algorithm is utilized to solve the robust optimization models. Case studies show that the solutions obtained from robust optimization models are better than the solutions obtained from the original integrated planning and scheduling when the prices are changed.

Keywords

Uncertainty, Robust Optimization, Integrated Problem of Planning and Scheduling, GA

1. Introduction

The integration technology of product planning and scheduling has received wide attentions in recent years [2]-[6]. Traditionally, these types of problems are treated under certain conditions. But as we all know, the environment changes every second, such as products prices, cost, and demands etc. Each of these changes can lead to the solutions not optimal or worse. So we must consider the uncertainty factors in the integration problem of planning and scheduling.

Robust optimization concept was first proposed by Soyster [7]; he used robust optimization to solve linear programming problems and found solutions which can be feasible with uncertainty under all possible distribution. The works of Ben-Tal & Nemirovski [8]-[11] made a clear direction to the robust optimization for future study. Since then, a considerable number of papers have appeared on the subject of robust optimization. Lin et al. (2004) [12] proposed a robust optimization approach for the scheduling of batch plants under processing times of tasks, market demands of product, prices of products and raw materials uncertainty. And the uncertain parameters are bounded. Janak et al. (2007) [13] proposed a new robust optimization approach for scheduling under uncertainty with known probability distribution base on the work of Lin et al. (2004) [12]. Verderame et al. (2009) [14] proposed a novel framework to address the problem of integration of operational planning and medium-term scheduling for large-scale industrial batch plants under demand and processing time uncertainty. The prices uncertainty was taken into account at planning level and processing time uncertainty was taken into account at scheduling level. They solved the proposed integrated mixed integer linear programming problem by means of a rolling horizon framework used in conjunction with a novel feedback loop. Li, Ding, Floudas (2011) [15] reviewed the robust optimization works before 2011, and studied six uncertainty sets (box set, ellipsoidal set, polyhedral, combined box and ellipsoidal set, combined box and polyhedral set, combined box, ellipsoidal and polyhedral set). They derived robust optimization formulations for the uncertainty on the left hand side, right hand side, and objective function of the classic model. Li et al. (2012) [16] concerned the planning model of large scale multiproduct continuous plants. They developed a MILP planning model based on discrete-time representation and presented robust optimization approach for demand and due date uncertainty.

To the best of our knowledge, until we write this paper, we first study the robust optimization model for the multi-product integrated problem of planning and scheduling under products prices uncertainty, and solve them with a bi-level genetic algorithm. At first, six uncertain sets are utilized to describe different products prices uncertainty. Then the robust models are proposed by the aforementioned uncertain sets and solved by genetic algorithm.

This paper is organized as follows: Section 1 is the history of the problem studied; Section 2 introduces the deterministic multi-product integrated model of planning and scheduling developed by Terrazas-Moreno & Grossmann [1]; Section 3 discusses the six uncertainty sets used to describe different uncertain prices; in Section 4, we present robust optimization models with the uncertainty sets in Section 3; Section 5 is the solution method based on genetic algorithm; Section 6 is the case studies of different robust optimization models; the last section is the conclusions.

2. Deterministic Multi-Product Integrated Problem of Planning and Scheduling

The deterministic multi-product integrated problem of planning and scheduling we based on in this paper is the work of Terrazas-Moreno & Grossmann (2011) [1]. With the objective of maximizing the total profits in planning time horizon, the planning section determines the amount of each product, each product distributed to each market, and the inventory level in each manufacturing site during each scheduling time period; the scheduling section determines the products sequence, start and end time of each product running in each production site during each scheduling time period.

The objective function of the deterministic integrated model of planning and scheduling under certain is as follows:

(2-1)

where i denote index of products, I denote set of products, m denote index of markets, M denote set of markets, s denote index of production site, S denote set of production site, t denote index of time periods, T denote set of time periods, 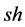denote the amount of product ship to the market, 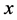denote the amount of product produced in site, 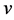denote inventory, 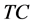denote transform cost, 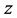and 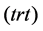denote transition between products.

Constraint formulations please refer the work of Terrazas-Moreno & Grossmann (2011) [1] to see more details. And there are 51 constraints in their model.

3. Six Uncertainty Sets Used in Robust Optimization

Firstly, we give the sets to describe the uncertain prices.

The box set: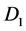

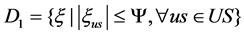(3-1)

where 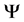is the adjustable parameter controlling the size of the uncertainty set, 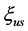denotes uncertainty,.

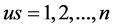The ellipsoidal set: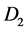

(3-2)

where is the adjustable parameter controlling the size of the uncertainty set.

The polyhedral set:

(3-3)

where is the adjustable parameter controlling the size of the uncertainty set.

The combined box and ellipsoidal set:

(3-4)

In order to ensure that the intersection between box and ellipsoidal set do not reduce to any one of them, the parameters should satisfy the following formulation

(3-5)

The combined box and polyhedral set:

(3-6)

In order to ensure that the intersection box and polyhedral set do not reduce to any one of them, the parameters should satisfy the following formulation.

(3-7)

The combined box, ellipsoidal and polyhedral set:

(3-8)

In order to ensure that the intersection box, ellipsoidal and polyhedral do not reduce to any one of them, the parameters should satisfy the following formulation.

(3-9)

(3-10)

4. Robust Models for the Integrated Planning and Scheduling under Products Prices Uncertainty

The constraint formulations are the same as the deterministic integrated model of planning and scheduling proposed by Terrazas-Moreno & Grossmann (2011) [1]. The products prices are in the objective function. We rewrite the objective function as (4-1).

(4-1)

“other” in (4-1) denotes production cost, shipment cost, inventory cost and transition cost.

The prices of products are denoted as (4-2).

(4-2)

where represent the uncertain prices of products i in market m; represent the nominal value of prices of products i in market m; represent constant value; are random values in uncertainty set.

We use the Formulations (4-3) and (4-4) to replace the Formulations (4-1) and (4-2).

(4-3)

(4-4)

Then, the robust optimization models for prices of products with different uncertainty sets are proposed.

The robust formulation for the box set

(4-5)

The robust formulation for ellipsoidal set

(4-6)

The robust formulation for polyhedral set

(4-7)

where is auxiliary variable.

The robust formulation for combined box and ellipsoidal set

(4-8)

where , are auxiliary variables.

The robust formulation for combined box and polyhedral set

(4-9)

where, are auxiliary variables.

The robust formulation for combined box, ellipsoidal and polyhedral set

(4-10)

where, , are auxiliary variables.

5. Solution Method Based on Genetic Algorithm

In this paper we use a bi-level genetic algorithm to solve the proposed robust optimization models in section 4. The flow diagram is described in Figure 1. Where denote whether product i is produced in site s in time period t, denote the production time variables for upper level problem, denote the production time variables for lower level problem, denote part of the transition time between time periods for lower level problem, denote part of the transition time between time periods for upper level problem, UB represent the upper level objective function values, UL represent the lower level objective objectives function values. The constraint formulations are the same as the deterministic integrated model of planning and scheduling proposed by Terrazas-Moreno & Grossmann (2011) [1].

6. Case Studies

We use the robust model proposed in section 4 and consider the products prices are uncertain. The parameters of the bi-level genetic algorithm are the population size (POP_SIZE = 30), max generations (GEN = 2000), cross rate (P_CROSSOVER = 0.3), mutation rate (P_MUTATION = 0.2), and tolarance (tol = 0.2). The uncertain products prices are as follows:

(6-1)

If the uncertain sets is described by box set, and. Then. Other uncertain sets are like the same.

Figure 2 shows the objectives of robust optimization under different uncertain sets. Figures 3-8 give the objectives of robust optimizaiton under the different uncertain sets compare to the objectives of deterministic integrated planning and scheduling model when the adjustable parameters are changed. In the combined box and ellipsoidal set, combined box and polyhedral set, combined box, ellipsoidal and polyhedral set,.

We can find that when the adjustable parameters () which controlling the size of the uncertainty sets are small, the difference between the objectives of deterministic integrated planning and scheduling model and

Figure 1. Flow chart of the genetic algorithm.

Figure 2. Robust optimization of different uncertain sets.

Figure 3. Box set.

Figure 4. Polyhedral set.

the objectives of the robust optimization models are small. But when the adjustable parameters () become larger, the objectives of the deterministic integrated planning and scheduling model are much smaller than

Figure 5. Ellipsoidal set.

Figure 6. Box+ polyhedral set.

Figure 7. Box+ ellipsoidal set.

the objectives of the robust model. We can conclude that the proposed robust optimization model are much better than the deterministic integrated planning and scheduling model when the products prices are changed.

Figure 8. Box+ polyhedral+ ellipsoidal set.

7. Conclusion

In this paper, we studied a robust optimization model for a multi-product integrated problem of planning and scheduling under products prices uncertainty. Six uncertain sets were utilized to describe different products prices uncertainty. Then the robust models were proposed by the aforementioned uncertain sets and solved by a bi-level genetic algorithm. The computing results from the case studies show that the proposed robust optimization models are much better than the deterministic integrated planning and scheduling model when the products prices are changed.

Acknowledgements

Financial support from the Shanghai commission of Nature Science (No. 12ZR1408100) is grateful appreciated.

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Terrazas-Moreno, S. and Grossmann, I.E. (2011) A Multiscale Decomposition Method for the Optimal Planning and Scheduling of Multisite Continuous Multiproduct Plants. Chemical Engineering Science, 66, 4307-4818. http://dx.doi.org/10.1016/j.ces.2011.03.017
[2]	Papageorgiou, L.G. and Pantelides, C.C. (1996) Optimal Campaign Planning/Scheduling of Multipurpose Batch/Semi- Continuous Plants. 1. Mathematical Formulation. Industrial and Engineering Chemistry Research, 35, 488-509. http://dx.doi.org/10.1021/ie950081l
[3]	Karimi, I.A. and Mcdonald, C.M. (1997) Planning and Scheduling of Parallel Semicontinuous Processes. 2. Short- Term Scheduling. Industrial and Engineering Chemistry Research, 36, 2691-2700. http://dx.doi.org/10.1021/ie9609022
[4]	Grossmann, I.E., Van Den Heever, S.A. and Harjunkoski, I. (2002) Discrete Optimization Methods and Their Role in the Integration of Planning and Scheduling. AIChE Symposium Series, 326, 150-168.
[5]	Lin, X., Floudas, C.A., Modi, S., et al. (2002) Continuous-Time Optimization Approach for Medium-Range Production Scheduling of a Multiproduct Batch Plant. Industrial and Engineering Chemistry Research, 41, 3884-3906. http://dx.doi.org/10.1021/ie011002a
[6]	Erdirik-Dogan, M. and Grossmann, I.E. (2006) A Decomposition Method for the Simultaneous Planning and Scheduling of Single-Stage Continuous Multiproduct Plants. Industrial and Engineering Chemistry Research, 45, 299-315. http://dx.doi.org/10.1021/ie050778z
[7]	Soyster, A.L. (1973) Convex Programming with Set-Inclusive Constraints and Appplications to Inexact Linear Programming. Operational Research, 21, 1154-1157. http://dx.doi.org/10.1287/opre.21.5.1154
[8]	Ben-Tal, A. and Nemirovski, A. (1998) Robust Convex Optimization. Mathematics of Operations Research, 4, 769- 805. http://dx.doi.org/10.1287/moor.23.4.769
[9]	Ben-Tal, A. and Nemirovski, A. (1999) Robust Solutions of Linear Programs. Operation, 25, 1-13.
[10]	Ben-Tal, A. and Nemirovski, A. (2000) Robust Solutions of Linear Programming Problems Contaminated with Uncertain Data. Methematical Programming, 88, 411-424. http://dx.doi.org/10.1007/PL00011380
[11]	Ben-Tal, A. and Nemirovski, A. (2002) Robust Optimization: Methodology and Applications. Math. Program. Ser. B, 92, 453-480. http://dx.doi.org/10.1007/s101070100286
[12]	Lin, X., Janak, S.L. and Floudas, C.A. (2004) A New Robust Optimization Approach for Scheduling under Uncertainty: I. Bounded Uncertainty. Computers & Chemical Engineering, 6, 1069-1085. http://dx.doi.org/10.1016/j.compchemeng.2003.09.020
[13]	Janak, S.L., Lin, X. and Floudas, C.A. (2007) A New Robust Optimization Approach for Scheduling under Uncertainty: II. Uncertainty with Known Probability Distribution. Computers & Chemical Engineering, 3, 171-195. http://dx.doi.org/10.1016/j.compchemeng.2006.05.035
[14]	Verderame, P.M. and Floudas, C.A. (2009) Operational Planning of Large-Scale Industrial Batch Plants under Demand Due Date and Amount Uncertainty. I. Robust Optimization Framework. Industrial & Engineering Chemistry Research, 48, 7214-7231. http://dx.doi.org/10.1021/ie9001124
[15]	Li, J., Verderame, P.M. and Floudas, C.A. (2012) Operational Planning of Large-Scale Continuous Processes: Deterministic Planning Model and Robust Optimization for Demand Amount and Due Date Uncertainty. Industrial & Engineering Chemistry Research, 51, 4347-4362. http://dx.doi.org/10.1021/ie202670a
[16]	Li, Z., Ding, R. and Floudas, C.A. (2011) A Comparative Theoretical and Computational Study on Robust Counterpart Optimization: I. Robust Linear Optimization and Robust Mixed Integer Linear Optimization. American Chemical Society, 50, 10567-10603.