1. Introduction
Natural electromagnetic fields in the ocean have two types of the sources: external (ionospheric and magnetospheric current systems) and internal one [1] . Internal source of electromagnetic field is the dynamo interaction of moving seawater with the Earth’s magnetic field [2] . From this point of view, seawater is considered as conducting continuum only and physical theory is used for suggested experiments and for interpretation of experimental data [3] [4] . However seawater is electrochemical system (multicomponent electrolytes solution) which is not uniform regarding to temperature and concentrations (salinity). Also seawater is subjected hydrostatic pressure along depth. Thermodynamics of electrolyte solutions experimentally and theoretically well establishes existence electric fields induced by gradients of concentrations, temperature and pressure (for example, [5] ). Nevertheless, experimental and theoretical considerations of the electrochemistry are never used for study of the electromagnetic fields in the ocean, excepting the case of preparation of electrodes, which are considered as “inert”. This paper attempts to partly eliminate gap between physics and electrochemistry in the study of electromagnetic field of the ocean. Some results have been published elsewhere [6] [7] .
2. Thermodynamic Background
Three important fluxes occur in a multicomponent electrolyte solutions: those of matter, heat, and electricity. These three fluxes are described by well-known laws of Fick, Fourier, and Ohm as being proportional to appropriate thermodynamic force. The more general case, where interactions between these processes occur, leads to a set of simultaneous equations which are formulated by non-equilibrium thermodynamics [8] .
Let us to consider seawater as n-components fully dissociated electrolyte solutions where each ion is assuming as component. When such electrolyte is subjected by thermodynamic forces then  fluxes should be induced which defined by equations:
fluxes should be induced which defined by equations:
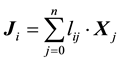 (1)
(1)
where 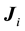 is the flux of
is the flux of 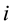 species;
species;  is
is 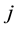 generalized thermodynamic force;
generalized thermodynamic force; 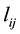 is the phenomenological coefficient which may be considered as generalized conductivity; index “0” corresponds to solvent (water). In further it will be used Hittorff’s reference frame for fluxes which means that
is the phenomenological coefficient which may be considered as generalized conductivity; index “0” corresponds to solvent (water). In further it will be used Hittorff’s reference frame for fluxes which means that
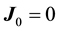 (2)
(2)
when system is in mechanical equilibrium. In the Equation (1)  thermodynamic forces are connected by generalized form of Gibbs-Duhem equation:
thermodynamic forces are connected by generalized form of Gibbs-Duhem equation:
 (3)
(3)
Here 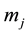 is molality of species
is molality of species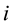 . Taking into account of Equations (2) and (3) the thermodynamic force and flux regarding to water can be excluded, then n independent fluxes may be expressed via
. Taking into account of Equations (2) and (3) the thermodynamic force and flux regarding to water can be excluded, then n independent fluxes may be expressed via  independent forces as follows
independent forces as follows
 (4)
(4)
Kirkwood et al. [9] demonstrated that when fluxes defined by the Hittorff’s reference frame (Equation (4)) then Onsager’s reciprocal relationships between phenomenological coefficients,  are fulfillment
are fulfillment
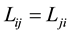 (5)
(5)
Existence of temperature, concentration, and gravitational field defines thermodynamic forces and Equation (4) can be rewritten as follows [8] :
![]() (6)
(6)
Here ![]() is molar mass of
is molar mass of ![]() species;
species; ![]() is the downward directed acceleration due to gravitational field;
is the downward directed acceleration due to gravitational field; ![]() is the charge number of ion
is the charge number of ion![]() ;
; ![]() is Fraday number;
is Fraday number; ![]() is electrical potential;
is electrical potential; ![]() is partial molal volume of the
is partial molal volume of the ![]() ion;
ion; ![]() is the entropy of transfer [10] ;
is the entropy of transfer [10] ; ![]() is temperature in Kelvin scale;
is temperature in Kelvin scale; ![]() is chemical potential of
is chemical potential of ![]() ion; upward direction is accepted as positive. At non-steady states, the electroneutral rule for electrolyte solutions is following [10] :
ion; upward direction is accepted as positive. At non-steady states, the electroneutral rule for electrolyte solutions is following [10] :
![]() (7)
(7)
where ![]() is electrical current. From mechanical equilibrium condition, the relationship is following:
is electrical current. From mechanical equilibrium condition, the relationship is following:
![]() (8)
(8)
Here ![]() is density of the solution. From the Equations (6), (7) and taking into account (8) the equation for gradient of electrical field is following
is density of the solution. From the Equations (6), (7) and taking into account (8) the equation for gradient of electrical field is following
![]() (9)
(9)
Due to reciprocal Onsager’s relationships (Equation (5)), the equation for transference number of species ![]() in Hittorff’s reference frame,
in Hittorff’s reference frame, ![]() , may be derived [11] as follows
, may be derived [11] as follows
![]() (10)
(10)
Taking into account that
![]() (11)
(11)
the equation for gradient of the chemical potential is following:
![]() (12)
(12)
Here![]() ,
, ![]() are activity and activity coefficient of the
are activity and activity coefficient of the ![]() ion, respectively;
ion, respectively; ![]() is gas universal constant. The final fundamental equation for gradient of electrical field in the electrolyte subjected under temperature, concentration and gravitational fields becomes from Equations (9)-(12)
is gas universal constant. The final fundamental equation for gradient of electrical field in the electrolyte subjected under temperature, concentration and gravitational fields becomes from Equations (9)-(12)
![]() (13)
(13)
3. Numerical Calculations of Electric Fields Induced in Seawater by Temperature, Concentration and Gravitational Fields
There are two problems of rigorous calculation of the Equation (13). Main problem is that thermodynamic properties of the individual ions cannot be strictly determined from thermodynamic point of view. Second problem is that there are a few experiments, which may to be used for numerical estimations of the Equation (13). Nevertheless, I try to carry out of numerical calculations of the Equation (13) using extrathermodynamic assumptions. These calculations have been approximated by empirical algorithms which provide a valuable tool for non-spe- cialists in thermodynamics working in the other research of the electromagnetic fields of the ocean.
The main feature of the seawater is that molality of major constituents of seawater exhibit an almost constant ratios to one another throughout the oceans. Therefore it is can be written as follows:
![]() (14)
(14)
Here, ![]() is proportional coefficient for
is proportional coefficient for ![]() species. This feature permits to introduce salinity,
species. This feature permits to introduce salinity, ![]() , into derivatives of chemical potential that simplifies the Equation (13)
, into derivatives of chemical potential that simplifies the Equation (13)
![]() (15)
(15)
Let us to introduce following notations:
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
Here ![]() is the module of the
is the module of the![]() ;
; ![]() is the barodiffusion potential with dimension [V/M];
is the barodiffusion potential with dimension [V/M]; ![]() is the thermodiffusion potential with dimension [V/grad];
is the thermodiffusion potential with dimension [V/grad]; ![]() is the diffusion potential with dimension [V/psu] where notation of psu (dimensionless “practical salinity unit”) expresses salinity as a mass fraction in per mill.
is the diffusion potential with dimension [V/psu] where notation of psu (dimensionless “practical salinity unit”) expresses salinity as a mass fraction in per mill.
3.1. Calculation of the Diffusion Potential in Seawater
For calculation diffusion potential, the composition of major constituents of seawater was taken from [12] and presented in Table 1. Transference numbers for given composition of seawater (Table 1) have been calculated from partial electrical conductances of major ions [13] and obtained values are listed in Table 1.
The derivatives of the activity coefficients of ions from salinity in the Equation (18) have been calculated by means of the Pitzer method (for example, [14] [15] ). The Pitzer method starts with a virial expansion of the excess Gibbs energy, ![]() , of the solution. The expressions for activity coefficients are obtained by appropriate derivatives of excess Gibbs energy with respect to weight of the solution,
, of the solution. The expressions for activity coefficients are obtained by appropriate derivatives of excess Gibbs energy with respect to weight of the solution, ![]() , and molality of the component
, and molality of the component![]() , respectively. Equations (19), (20) give the expressions for the activity coefficients of cations
, respectively. Equations (19), (20) give the expressions for the activity coefficients of cations![]() , anions
, anions ![]() species, respectively.
species, respectively.
![]() (19)
(19)
![]() (20)
(20)
The parameters appearing in the Equations (19)-(20) are defined as follows:
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
Here “a”, “c” and “n” are cations, anions and neutral species, respectively. ![]() is the Debye-Hueckel limiting slope with numerical values calculated according to an empirical equation suggested by Clegg and Whitfield [16] . For non-associated electrolytes
is the Debye-Hueckel limiting slope with numerical values calculated according to an empirical equation suggested by Clegg and Whitfield [16] . For non-associated electrolytes ![]() and
and ![]() take values of 2 and 0, respectively, whereas for 2 - 2 electrolytes the optimized values of
take values of 2 and 0, respectively, whereas for 2 - 2 electrolytes the optimized values of ![]() and
and ![]() are 1.4 and 12 kg1/2∙mol−1/2, respectively.
are 1.4 and 12 kg1/2∙mol−1/2, respectively. ![]() and
and ![]() are the ionic strength derivatives of
are the ionic strength derivatives of ![]() and
and![]() ,
, ![]() is ionic strength, and
is ionic strength, and![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , are measurable empirical constants (Pitzer parameters);
, are measurable empirical constants (Pitzer parameters);![]() ,
, ![]() are immeasurable second and third viral coefficients, respectively in the Pitzer method. The Equations (19), (20) contain measurable and immeasurable segment. Fortunately, the immeasurable virial coefficients contained in brackets for many cases are not significant and can be neglected. The Pitzer parameters applied in our calculations of the Equations (19), (20) were taken from the literatures which cited elsewhere [17] . Numerical calculations were carried out for 30 - 40 salinity range and for 273 - 298 K temperature range. Results of calculations were approximated by following empirical relationship.
are immeasurable second and third viral coefficients, respectively in the Pitzer method. The Equations (19), (20) contain measurable and immeasurable segment. Fortunately, the immeasurable virial coefficients contained in brackets for many cases are not significant and can be neglected. The Pitzer parameters applied in our calculations of the Equations (19), (20) were taken from the literatures which cited elsewhere [17] . Numerical calculations were carried out for 30 - 40 salinity range and for 273 - 298 K temperature range. Results of calculations were approximated by following empirical relationship.
![]() (26)
(26)
3.2. Calculation of the Barodiffusion Potential in Seawater
For calculations of Equation (16), needed the partial molal volumes of the major ions of seawater are given as function salinity and temperature elsewhere [18] . Used molar masses of ions are tabulated in the Table 1. Densities of seawater were calculated using EOS of seawater [19] . Numerical calculations of the Equation (16) were carried out for 30 - 40 salinity range and for 273 - 298 K temperature range. Results of the calculations were approximated by following empirical relationship
![]() (27)
(27)
3.3. Calculation of the Thermodiffusion Potential in Seawater
Non-isothermal properties of the electrolyte solutions are weakly studied as experimentally and theoretically as well. On this reason, the thermodiffusion properties of the 0.7 m NaCl have been used for estimation of the thermodiffusion potential in seawater. In this case Equation (17) is significantly simplified
![]() (28)
(28)
The “absolute” entropies of transfer of sodium and chloride ions for 298 K have been published elsewhere [20] . The transference numbers in Hittorff’s reference frame for 0.7 molality sodium chloride solution have been taken from [21] . Numerical calculation of the Equation (28) gives relationship
![]() (29)
(29)
4. Discussion
The scalar fields of the salinity, temperature and gravity cause diffusion of ions. Due to differences in physicochemical properties for each species of the electrolyte solution (mobility, activity coefficients, entropy of transfer, molar masses, and partial molal volume), the diffusion of ions induces electric field inside in seawater. Main feature of the diffusion processes in the electrolyte solutions is fulfillment of electroneutrality on the macroscopic space scale [22] . Another feature is that for diffusion process the electric relaxation time is about 10−8 sec or less [23] . Last feature means that during 10−8 sec electric field becomes steady state after sharp formed scalar fields. On these reasons diffusion-induced electric field can be considered as distribution of dipoles.
With the purpose of an estimation of possible impact![]() ,
, ![]() fields of the ocean on electric field, the diffusion-induced electric field have been calculated for given
fields of the ocean on electric field, the diffusion-induced electric field have been calculated for given![]() ,
, ![]() profiles (
profiles (![]() is temperature in centigrade scale). These profiles were measured on R/V Sonne S0178 in July 2004 on the slope of the Sakhalin Island (Sea of Okhotsk) (Figure 1(a)). For these profiles, the differences in diffusion potentials between surface and given depth have been calculated using Equations (26), (27), and (29) and results are presented on the Figure 1(b). As it is seen from Figure 1, the order of magnitude of the electric field induced by diffusion has similar order
is temperature in centigrade scale). These profiles were measured on R/V Sonne S0178 in July 2004 on the slope of the Sakhalin Island (Sea of Okhotsk) (Figure 1(a)). For these profiles, the differences in diffusion potentials between surface and given depth have been calculated using Equations (26), (27), and (29) and results are presented on the Figure 1(b). As it is seen from Figure 1, the order of magnitude of the electric field induced by diffusion has similar order
![]()
Table 1. Parameters of seawater used for calculations of the diffusion potential.
![]()
Figure 1. (a) t, S profiles obtained from CTD data on R/V Sonne S0178 in July 2004 (St. 39) on the slope of the Sakhalin Island (Sea of Okhotsk); (b) Calculated profiles of differences in diffusion potentials between surface and given depth using Equations (26), (27), (29).
with those induced by geostrophic currents. Obviously, time-space variations in temperature-salinity structure of the sea have to generate variations in the structure of the electric field. For estimations of these fluctuations, ![]() ,
, ![]() profiles obtained for two hydrological stations implemented in 13-th and 15-th August 2004 at the same place (54˚26.8'N, 144˚4.1'E) were taken. Variations in
profiles obtained for two hydrological stations implemented in 13-th and 15-th August 2004 at the same place (54˚26.8'N, 144˚4.1'E) were taken. Variations in![]() ,
, ![]() profiles were generated by simple subtraction of
profiles were generated by simple subtraction of![]() ,
, ![]() data between stations 53 (15-th Aug.) and 39 (13-th Aug.), respectively. Figure 2(a) demonstrates them. Since these stations situated in the area of the intermediate water formation of the Okhotsk Sea, then strong time-variations of
data between stations 53 (15-th Aug.) and 39 (13-th Aug.), respectively. Figure 2(a) demonstrates them. Since these stations situated in the area of the intermediate water formation of the Okhotsk Sea, then strong time-variations of![]() ,
, ![]() parameters are observed. Variations of the electrical field corresponded variations of
parameters are observed. Variations of the electrical field corresponded variations of![]() ,
, ![]() parameters are shown on Figure 2(b).
parameters are shown on Figure 2(b).
From Figure 1, Figure 2 it is following that for interpretation of the oceanic electric field measurements, the contribution of diffusion processes into electric field should be taken into account. For this reason, implementation of the electric field measurements should be supplemented by hydrological observations.
Geological and geochemical processes may cause thermal and concentration anomalies, which give anomalies in the electric field. For example, magnetic and electric field variations associated with eruption of volcano where observed and summarized elsewhere [24] . In coastal area incursion of seawater into fresh-water aquifers may to create strong concentration gradients, which induce anomaly of electric field [25] . I think that commonly known in thermodynamic electrolyte solutions, the Equation (13), must be involved into interpretation of observed anomalies of the electric field.
Numerical calculations of Equation (13) in application to seawater have two different sources of uncertainty. One of them is fundamental problem, which may be formulated as impossibility of rigorous determination of thermodynamic properties of the individual ions. It means that thermodynamic properties of electroneutral combination of ions can be determined (measured) only. For example, entropies of transfer, activity coefficients (or derivatives of them), and partial molar volumes for salts (NaCl, Na2SO4, etc.) in multicomponents of electrolyte solution can be determined but not for individual ions. On this reason extrathermodynamic assumptions are necessary for evaluation of the thermodynamic properties of individual ions. Activity coefficients of the individual ions and them derivatives were calculated by means of Equations (19)-(25) neglecting by last bracket in Equations (19), (20). There are many evidences that adequately experimental uncertainty, the Equations (19) and (20) describe non-ideal behavior of salts for any components of electrolyte solutions (activity coefficients, osmotic coefficients and them derivatives from concentrations, temperature, and pressure). Moreover, contributions of the Pitzer parameters, taking into account interactions between like-charged ions and interactions between three species are very small as rule. It is should be noted that Pitzer parameters are electroneutral combination of the corresponding virial coefficients. The last bracket of the Equations (19), (20) contains just the second virial
![]()
Figure 2. (a) Variations of t, S-profile obtained by simple subtraction of t. S data between stations 53 and 39 implemented on R/V Sonne S0178 in 15-th and 13- th July, respectively; (b) Variations of the electrical field corresponded variations of t, S parameters.
coefficients taking into account interactions between the same ions (for example, ![]() or
or![]() ) and third virial coefficients taking into account triplet interactions. All available experimental data demonstrate that contribution of this type of interactions as in last bracket may be neglected for simple ions such as major ions of seawater and ionic strength less 1 (
) and third virial coefficients taking into account triplet interactions. All available experimental data demonstrate that contribution of this type of interactions as in last bracket may be neglected for simple ions such as major ions of seawater and ionic strength less 1 (![]() at
at![]() ). Another words, the Pitzer method is enough accurate for estimation the activity coefficients and them derivatives for individual ions of seawater. Poisson and Chanu [26] discussed splitting of the partial molar volumes of major seawater salts on ionic constituents. They made a number of assumptions which discussion beyond of this report. De Bethune and Daley [20] obtained ionic entropies of transfer using Agar’s reasonable assumption that
). Another words, the Pitzer method is enough accurate for estimation the activity coefficients and them derivatives for individual ions of seawater. Poisson and Chanu [26] discussed splitting of the partial molar volumes of major seawater salts on ionic constituents. They made a number of assumptions which discussion beyond of this report. De Bethune and Daley [20] obtained ionic entropies of transfer using Agar’s reasonable assumption that ![]() in 0.01 m KCl solution.
in 0.01 m KCl solution.
Another important source of uncertainty of the suggested Equations (26), (27), and (29) is quality of available experimental data. At present time, there is a very good dataset of the Pitzer parameters [27] . Partial molal volumes of sea salts are well studied also [18] . The partial electrical conductances of major ions in seawater were actually measured at ![]() and
and![]() . However, they are used calculations of transference numbers for 30‰ - 40‰ and 273 - 298 K salinity and temperature ranges, respectively. Using of these transference numbers for expanded salinity and temperature range gives some error in our calculation which difficult to estimate. Thermodiffusion properties of electrolyte solutions are weakly studied, especially in multicomponent electrolyte solutions as experimentally and theoretically as well. Therefore, estimation gradient of electric potential induced by temperature gradient by means of relationship (29) is rather qualitative. There is way of “experimental determination” of contributions of salinity, temperature, and pressure gradients into formation of the electric potential gradient in seawater. I take “experimental determination” into inverted commas because it was below suggested that experiments should be supplemented additional extrathermodynamic assumptions.
. However, they are used calculations of transference numbers for 30‰ - 40‰ and 273 - 298 K salinity and temperature ranges, respectively. Using of these transference numbers for expanded salinity and temperature range gives some error in our calculation which difficult to estimate. Thermodiffusion properties of electrolyte solutions are weakly studied, especially in multicomponent electrolyte solutions as experimentally and theoretically as well. Therefore, estimation gradient of electric potential induced by temperature gradient by means of relationship (29) is rather qualitative. There is way of “experimental determination” of contributions of salinity, temperature, and pressure gradients into formation of the electric potential gradient in seawater. I take “experimental determination” into inverted commas because it was below suggested that experiments should be supplemented additional extrathermodynamic assumptions.
I suggest to measure diffusion, thermodiffusion, and barodiffusion potential by means of measurements of electromotive forces (EMF) following cells:
EMF of the cells (A), (B), (C) may be writing respectively:
![]() (30)
(30)
![]() (31)
(31)
![]() (32)
(32)
where, ![]() and
and ![]() are respectively, temperature and pressure coefficients of the
are respectively, temperature and pressure coefficients of the
following electrode reaction:
![]() (33)
(33)
Here, subscription “s” means solid. I suggest using of rather synthetic seawater than natural seawater because natural seawater contains ![]() and
and ![]() ions which interference potential of silver-silver chloride electrode. Estimation diffusion, thermodiffusion and barodiffusion potentials via measurements of the EMF of cells (A)-(C) is shortest way with minimum amount of extrathermodynamic assumptions. However, noise of the silver electrode does not permit to carry out accurate measurements of the
ions which interference potential of silver-silver chloride electrode. Estimation diffusion, thermodiffusion and barodiffusion potentials via measurements of the EMF of cells (A)-(C) is shortest way with minimum amount of extrathermodynamic assumptions. However, noise of the silver electrode does not permit to carry out accurate measurements of the ![]() even when seawater column would has a few meters because expected measured magnitude has order about 10−6 V. In this case centrifugal cells should be used [28] . It is should be noted that contribution of barodiffusion into electric field of the ocean is almost constant (about −3 × 10−7 V/M) and in many cases of electrical fields study it can be negligible.
even when seawater column would has a few meters because expected measured magnitude has order about 10−6 V. In this case centrifugal cells should be used [28] . It is should be noted that contribution of barodiffusion into electric field of the ocean is almost constant (about −3 × 10−7 V/M) and in many cases of electrical fields study it can be negligible.
5. Conclusions
Electrochemical processes such as diffusion, thermodiffusion, and barodiffusion induce electric field in the ocean due to existence of natural salinity, temperature, and gravitational fields. Diffusion-induced electric field can be considered as distribution of dipoles.
Natural variations of hydrological properties cause variations of electric field in seawater.
Geological and geochemical processes, which induce thermal and concentration anomalies, may result in anomalies in the electric field.
Using of the chemical model of seawater, the Pitzer method for calculations of non-ideal behavior of electrolyte solutions, and available thermodynamic data for major ions of seawater, the numerical calculation of Equation (13) was carried out. Results of numerical calculations are represented by empirical relationships which are easy to apply to any modeling.
Modern theoretical and experimental knowledge of the thermodynamic properties of multicomponent electrolyte solutions does not permit to quantitatively describe diffusion-induced electric field in the ocean. On this reason it is suggested to carry out special potentiometric experiments with synthetic seawater for accurate estimation diffusion-induced electric field in seawater.