Unsteady Incompressible Flow of a Generalized Oldroyd-B Fluid between Two Oscillating Infinite Parallel Plates in Presence of a Transverse Magnetic Field ()
1. Introduction
The magneto hydrodynamic flow problem between two parallel plates has shown immense attention during the last several decades. The study has significant applications in the field of hydrodynamical machines and apparatus, magnetic storage devices, computer storage devices, lubrication, crystal growth processes, radial diffusers, MHD pumps, MHD power generators, purification of crude oil, petroleum industries etc. Bandelli et al. [1] discussed start-up flows of second grade fluids in domains with one finite dimension. Fetecau et al. [2] investigated exact solutions for the flow of a generalized Oldroyd-B fluid induced by a constantly accelerating plate between two side walls perpendicular to the plate. Hayat et al. [3] made homotopy analysis of MHD boundary layer flow of an upper-convected Maxwell fluid. Jamil and Khan [4] studied slip effects on fractional viscoelastic fluids. Shen et al. [5] studied the Rayleigh-Stokes problem for a heated generalized second grade fluid with fractional derivative model. Vieru et al. [6] discussed the flow of a generalized Oldroyd-B fluid due to a constantly accelerating plate. Wenchang et al. [7] investigated unsteady flows of a viscoelastic fluid with the fractional Maxwell model between two parallel plates. Vieru et al. [8] studied the unsteady flow of a generalized Oldroyd-B fluid due to an infinite plate subject to a time-dependent shear stress.
In the present paper we consider the flow of a generalized Oldroyd-B fluid between two oscillating infinite parallel plates in presence of transverse magnetic field. We have formulated the expression for the velocity field for the said flow in terms of Mittage-Leffler function. In the constitutive equation of the fluid model, the time derivative of integral order has been replaced by Riemann-Liouville fractional calculus operator. The exact solution for the velocity field is obtained by using the method of integral transformations and the dependence of the said field on the material as well as fractional calculus parameters is illustrated graphically.
2. Mathematical Formulation and Basic Equation
Let us consider an incompressible generalized Oldroyd-B fluid bounded by two infinite parallel plates as shown in Figure 1. The plates are initially at rest and at 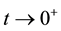 the plates start to oscillate in its plane with the velocity
the plates start to oscillate in its plane with the velocity 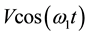 and
and 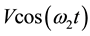 where
where  is the fluid velocity. Due to the shear, the fluid is moved gradually. We have taken Cartesian coordinate system. x- and y-coordinates are taken along and perpendicular to the parallel plates respectively. Accordingly, the initial condition is given by
is the fluid velocity. Due to the shear, the fluid is moved gradually. We have taken Cartesian coordinate system. x- and y-coordinates are taken along and perpendicular to the parallel plates respectively. Accordingly, the initial condition is given by ,
,  and the boundary conditions are given by
and the boundary conditions are given by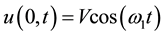 ,
,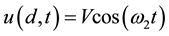 .
.
We take the velocity and stress of the form
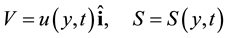 (1)
(1)
where  is the velocity component in the x-direction.
is the velocity component in the x-direction.
The constitutive relationship for the fluid associated with the present problem is given by,
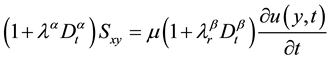 (2)
(2)
In the relation (2),  and
and 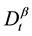 are Caputo operators defined by
are Caputo operators defined by
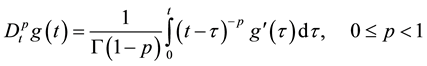 (3)
(3)
According to our problem,
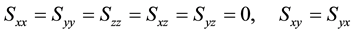
We consider a generalized Oldroyd-B fluid between two infinite parallel disks in presence of an imposed magnetic field ![]() that acts in the direction of the positive y-axis. Then in the presence of the body force
that acts in the direction of the positive y-axis. Then in the presence of the body force![]() , the momentum equation is given by
, the momentum equation is given by
![]() (4)
(4)
where “![]() ” is constant and “
” is constant and “![]() ” is the density of the fluid.
” is the density of the fluid.
Eliminating ![]() between the Equations (2) and (4) we have the governing equation
between the Equations (2) and (4) we have the governing equation
![]() (5)
(5)
where ![]() is the kinematic viscosity and
is the kinematic viscosity and ![]()
Introducing the non-dimensional quantities,
![]()
![]()
we get the governing equation in non-dimensional quantities as
![]() (6)
(6)
(Omitting the dimensionless mark “*”)
![]() (7)
(7)
and the boundary conditions![]() , for
, for ![]()
![]() (8)
(8)
Taking finite Fourier sine transformation we get from Equation (6)
![]() (9)
(9)
where ![]() is the finite Fourier sine transformation of
is the finite Fourier sine transformation of![]() .
.
Using the boundary conditions (8) the Equation (9) can be rewritten as
![]() (10)
(10)
Taking Laplace transformation and using ![]() we get from the above equation
we get from the above equation
![]() (11)
(11)
Now in order to avoid the lengthy procedure of residues and contour integrals, we rewrite the Equation (11) into series form as
![]() (12)
(12)
Now we have an important Laplace transformation of the nth order derivative of Mittage-Leffler function ![]() given by
given by
![]() (13)
(13)
where
![]() (14)
(14)
Taking Laplace Inverse transformation we get from the Equation (12)
![]() (15)
(15)
Taking inverse finite Fourier sine transformation we get the velocity profile from the Equation (18) as
![]() (16)
(16)
3. Limiting Cases
Case-I If![]() ,
, ![]() then the equation of motion is given by
then the equation of motion is given by
![]() (17)
(17)
subject to the initial and boundary conditions given by the Equations (7) and (8) respectively.
The Equation (17) represents the governing equation of a classical Newtonian fluid and the corresponding velocity field is given by
![]() (18)
(18)
Case-II If![]() ,
, ![]() then the equation is given by
then the equation is given by
![]() (19)
(19)
subject to the initial and boundary conditions given by the Equations (7) and (8).
The Equation (19) represents the governing equation of a generalized Maxwell fluid and the corresponding velocity field is given by
![]() (20)
(20)
Case-III If![]() ,
, ![]() then the equation of motion is given by
then the equation of motion is given by
![]() (21)
(21)
subject to the initial and boundary conditions given by the Equations (7) and (8) respectively.
The Equation (21) is the governing equation for a generalized second grade fluid and the velocity field is given by
![]() (22)
(22)
Case-IV If![]() ,
, ![]() then the equation of motion is given by
then the equation of motion is given by
![]() (23)
(23)
subject to the initial and boundary conditions given by the Equations (7) and (8) respectively.
The Equation (23) represents the governing equation of an ordinary Oldroyd-B fluid and the corresponding velocity field is given by
![]() (27)
(27)
4. Conclusions and Numerical Results
In this paper we have presented the flow of a generalized Oldroyd-B fluid between two oscillating infinite parallel plates. The velocity field has been determined by means of Laplace and finite Fourier sine transformations in series form in terms of Mittage-Leffler function. The dependence of the velocity field on the fractional calculus parameters and material parameters has been illustrated graphically. The solutions for the four limiting cases have been discussed from the solution of the flow problems of a generalized Oldroyd-B fluid.
In Figure 2 the velocity is depicted against the distance from the lower plate for different values of the fractional calculus parameter![]() . As
. As ![]() increases, the fluid velocity increases and there are points of local minimum and local maximum in the velocity curves which are oscillatory in nature. Negative velocity can be observed near the upper plate for values of
increases, the fluid velocity increases and there are points of local minimum and local maximum in the velocity curves which are oscillatory in nature. Negative velocity can be observed near the upper plate for values of ![]() near zero in Figure 2. The velocity is depicted against the distance from the lower plate for different values of fractional calculus parameter
near zero in Figure 2. The velocity is depicted against the distance from the lower plate for different values of fractional calculus parameter ![]() in Figure 3. As
in Figure 3. As ![]() increases, the fluid velocity decreases, which is opposite to the case in Figure 2 and the points of local minimum and maximum can be observed in the velocity curves. The flow patterns are oscillatory in nature. In Figure 4 the velocity is plotted against the distance from the lower plate for different values of the parameter M. As the parameter M takes increasing values, the fluid velocity increases and the velocity curves are oscillatory in nature. The velocity profile is plotted against the distance from the lower plate for different values of the frequency of oscillation
increases, the fluid velocity decreases, which is opposite to the case in Figure 2 and the points of local minimum and maximum can be observed in the velocity curves. The flow patterns are oscillatory in nature. In Figure 4 the velocity is plotted against the distance from the lower plate for different values of the parameter M. As the parameter M takes increasing values, the fluid velocity increases and the velocity curves are oscillatory in nature. The velocity profile is plotted against the distance from the lower plate for different values of the frequency of oscillation ![]() of the lower plate in Figure 5. It is evident from the figure that the fluid velocity decreases for higher values of the parameter
of the lower plate in Figure 5. It is evident from the figure that the fluid velocity decreases for higher values of the parameter![]() . The initial points of the velocity curves near the lower plate are different in domain of spatial
. The initial points of the velocity curves near the lower plate are different in domain of spatial
variable Y for different values of frequency of oscillation ![]() of the lower plate. There is negative velocity in Figure 5 near the lower plate for values for higher frequency of oscillation of the lower plate. In Figure 6 as the frequency of the oscillation
of the lower plate. There is negative velocity in Figure 5 near the lower plate for values for higher frequency of oscillation of the lower plate. In Figure 6 as the frequency of the oscillation ![]() of the upper plate changes, the terminal points of the velocity curves near the upper plate differ. The fluid velocity decreases with the increase of the frequency of oscillation
of the upper plate changes, the terminal points of the velocity curves near the upper plate differ. The fluid velocity decreases with the increase of the frequency of oscillation ![]() of the upper plate near that one. It can be noticed that there are points of local minimum and maximum for velocity curves for all the three cases. Negative velocity can be observed near the upper plate in Figure 6 for higher values of the frequency of oscillation of the upper plate. In Figure 7 the velocity profile is depicted against the distance from the lower plate for different values of the parameter
of the upper plate near that one. It can be noticed that there are points of local minimum and maximum for velocity curves for all the three cases. Negative velocity can be observed near the upper plate in Figure 6 for higher values of the frequency of oscillation of the upper plate. In Figure 7 the velocity profile is depicted against the distance from the lower plate for different values of the parameter ![]() in which the frequencies of oscillations of the plates are equal i.e.
in which the frequencies of oscillations of the plates are equal i.e.![]() . The fluid velocity increases with increasing values of
. The fluid velocity increases with increasing values of ![]() and the velocity curves are oscillatory in nature. It can be noticed that for equal frequency of oscillations of the two plates, the heights of the initial and terminal points on the velocity curve in the domain of spatial variable are equal.
and the velocity curves are oscillatory in nature. It can be noticed that for equal frequency of oscillations of the two plates, the heights of the initial and terminal points on the velocity curve in the domain of spatial variable are equal.