Using the Resistance Depending on the Magnetic and Electric Susceptibility to Derive the Equation of the Critical Temperature ()
1. Introduction
In superconductors, the resistance is zero at temperatures less than the critical temperature [1] ; in this work, the above concept is proved by taking the conductivity as a function of the permittivity and permeability, and within the existence of the conditions that make the resistance be equal to zero or approach to infinity.
2. Resistivity Formula Due to the Permeability and Permittivity
When the temperature of a conductor approach to the absolute zero, the friction resistance can be ignored [2] , if an electron e is induced by an electric field E, then the force on it is given by
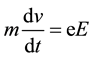 (1)
(1)
Including the position variable  in Equation (1) it can be written as
in Equation (1) it can be written as
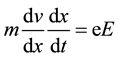 (2)
(2)
Then
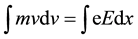 (3)
(3)
According to the definition of the potential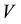 , we get
, we get
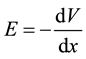 (4)
(4)
From Equation (3)
 (5)
(5)
Then
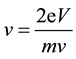 (6)
(6)
While  is constant, and when the potential difference is constant, then the velocity
is constant, and when the potential difference is constant, then the velocity 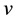 is being also constant.
is being also constant.
Using Equation (6) and substituting the value of 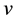 in the equation of current, that given due to the electron velocity
in the equation of current, that given due to the electron velocity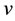 , charges density
, charges density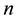 , and the area
, and the area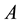 ,
, 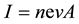 , then the current
, then the current 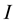 is found to be
is found to be
![]() (7)
(7)
Then the resistance ![]() is given
is given
![]() (8)
(8)
On other hand ![]() can be written due to the resistivity
can be written due to the resistivity![]() , the length
, the length![]() , and the crossection area as
, and the crossection area as
![]() (9)
(9)
Considering the electron as a wave, its velocity becomes [3]
![]() (10)
(10)
Accordingly the resistivity is given by
![]() (11)
(11)
3. Critical Temperature at a Changing Permeability µ
If a magnetic field with a flux density![]() , an electric force
, an electric force![]() , besides a friction resistance
, besides a friction resistance![]() , and a pressure
, and a pressure
force ![]() act together, then the centripetal forces which balance this force is given by [4] .
act together, then the centripetal forces which balance this force is given by [4] .
![]() (12)
(12)
where ![]() is the radial velocity, while the friction force and the pressure are given by
is the radial velocity, while the friction force and the pressure are given by
![]() (13)
(13)
where ![]() is the friction coefficient.
is the friction coefficient.
![]()
when the outer magnetic field vanishes, then the radial velocity becomes
![]() (14)
(14)
And
![]() (15)
(15)
where ![]() denotes the inner magnetic field.
denotes the inner magnetic field.
And when an outer magnetic field ![]() is applied, then
is applied, then
![]() (16)
(16)
where ![]() is the radial force, and
is the radial force, and![]() ,
, ![]() are the magnetic and the electric forces respectively, which are given by
are the magnetic and the electric forces respectively, which are given by
![]() (17)
(17)
The equation of motion in the presence of the outer magnetic field is given in the form [5] .
![]() (18)
(18)
where ![]() is the radial velocity, and while
is the radial velocity, and while ![]() then
then
![]() (19)
(19)
when ![]() is so closed to
is so closed to ![]() then
then
![]() and
and
![]()
where ![]() is Larmar frequency, substitute Equation (15) and Equation (19) one gets?
is Larmar frequency, substitute Equation (15) and Equation (19) one gets?
![]()
![]()
![]()
Dividing both sides by ![]() we get
we get
![]() (20)
(20)
![]() (21a)
(21a)
The current for one atom with ![]() electrons, moving around its nucleus with a frequency f is
electrons, moving around its nucleus with a frequency f is
![]() (21b)
(21b)
where ![]() is the atomic number,
is the atomic number, ![]() is the electron charge, and
is the electron charge, and ![]() is Larmar frequency.
is Larmar frequency.
The magnetic torque for one atom is given by
![]() (22)
(22)
where ![]() is the area surrounded by the current which is equal
is the area surrounded by the current which is equal
![]()
And from Figure 1, one get:
![]()
But
![]()
![]() (23)
(23)
So the magnetic torque for one atom ![]() becomes
becomes
![]()
Figure 1. Magnetic torque in Z direction.
![]() (24)
(24)
If the number of atoms per unit volume is assumed to be ![]() then, the magnetic torque for the matter is
then, the magnetic torque for the matter is
![]() (25)
(25)
![]() (26)
(26)
According to the definition of susceptibility ![]() then [6] .
then [6] .
![]() (27)
(27)
Comparing Equations (26) and (27) the susceptibility being
![]() (28)
(28)
Then the resistivity in Equation (11) becomes
![]() (29)
(29)
where ![]() denotes the photon energy.
denotes the photon energy.
The resistivity ![]() is imaginary, and the real resistivity vanishes when
is imaginary, and the real resistivity vanishes when
![]()
or ![]() (30)
(30)
Accordingly the critical temperature becomes
![]() (31)
(31)
4. Calculating the Critical Temperature Due to the Conductivity
Assuming that the charges in the conductor are acted by a resistance force![]() , and a magnetic force
, and a magnetic force![]() , besides the electric force
, besides the electric force![]() , and then the equation of motion becomes [7] .
, and then the equation of motion becomes [7] .
![]() (32)
(32)
The previous forces are given by the formulas
![]()
where ![]() and
and ![]() denotes the density, rigidity coefficient, displacement, mass, velocity, electron charge, magnetic flux density, resolving time, and the electric field respectively.
denotes the density, rigidity coefficient, displacement, mass, velocity, electron charge, magnetic flux density, resolving time, and the electric field respectively.
The equation of motion takes the formula
![]() (33)
(33)
When the electron moves with a uniform constant velocity, the Equation (33) becomes
![]() (34)
(34)
And the conductivity is given by
![]() (35)
(35)
where ![]() the electrons density, while
the electrons density, while ![]() denotes the density of the medium atoms, accordingly the conductivity being
denotes the density of the medium atoms, accordingly the conductivity being
![]() (36)
(36)
And the conductivity approaches to infinity when
![]() (37)
(37)
According to the Maxwell-Boltzmann statistics the density of the atoms in the medium takes the formula [8] .
![]()
Then
![]()
![]()
![]() (38)
(38)
Equation (38) represents the critical temperature in which the conductivity becomes very huge, and when
![]() (39)
(39)
The conductivity also becomes very high, and then
![]() (40)
(40)
![]()
![]() (41)
(41)
And finally the critical temperature is found to be
![]() (42)
(42)
5. Discussion
The classical rules of the electron motion in Equation (1) are used to find the classical formula of the resistivity given in Equation (11), and the electron is considered to be a wave according to the quantum principles and this clarified that the resistivity is a function of the electric and magnetic susceptibility.
The interpretation of Equation (28)―in which we derived the magnetic susceptibility from the electron equation of motion, that depend on the friction force within the friction coefficient![]() , the inner magnetic field
, the inner magnetic field![]() , the grad of the electrons density
, the grad of the electrons density![]() , and the atom radius
, and the atom radius![]() ―is that when Equation (28) is substituted in Equation (11) the critical temperature at which the resistance vanishes, was found to be in the form that given by Equation (31), which was completely depends on the inner magnetic field
―is that when Equation (28) is substituted in Equation (11) the critical temperature at which the resistance vanishes, was found to be in the form that given by Equation (31), which was completely depends on the inner magnetic field![]() , and the friction, within the coefficient
, and the friction, within the coefficient![]() , the radius
, the radius![]() , and the grad of the electron density
, and the grad of the electron density![]() .
.
When we considered the electron motion due to the impact of an inner magnetic field, and a friction resistance, the conductivity was found to be as shown in Equation (36).
The mathematical analysis interprets that the conductivity becomes very high at temperatures less than the critical temperature, which depends on the friction resistance and the inner magnetic field as shown in Equations (41)-(42).
6. Conclusion
The model in which the resistance depends on the electric and magnetic susceptibility, clarifies that the resistance vanishes, and the metal becomes a superconductor at the critical temperature and the temperatures less than it; this relation is not clear in the famous models of the superconductivity.