1. Introduction
In the Keplerian problem, a body of mass  follows a conic orbit, for which the focus is identified to the center of attracting body (with mass
follows a conic orbit, for which the focus is identified to the center of attracting body (with mass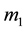 ). The Keplerian motion is described by the fundamental differential equation of the physical two-body problem:
). The Keplerian motion is described by the fundamental differential equation of the physical two-body problem:
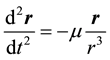 (1)
(1)
where 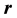 is the vector position of the moving body related to the attraction center and
is the vector position of the moving body related to the attraction center and 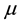 the gravitational parameter defined by
the gravitational parameter defined by 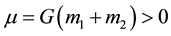 (where
(where 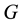 the Newtonian gravitational constant) (see [1] , Equation (6.2.3)).
the Newtonian gravitational constant) (see [1] , Equation (6.2.3)).
The traditional form of Kepler’s equation, which can be obtained directly from Equation (1) (see [1] , Section 6.3 and [2] ), is normally written as:
For elliptic orbits 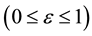
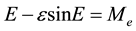 (2a)
(2a)
for hyperbolic orbits 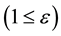
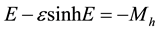 (2b)
(2b)
where 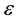 is the eccentricity,
is the eccentricity, 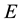 the eccentric anomaly and
the eccentric anomaly and 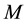 the mean anomaly, which is defined as
the mean anomaly, which is defined as
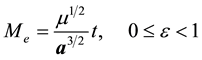 (2c)
(2c)
![]() (2d)
(2d)
![]() (2e)
(2e)
(see [2] , Equation (11) and [3] , Equations (4.35) and (4.51)). Remark that the time ![]() is measured from pericenter and
is measured from pericenter and ![]() is the semimajor axis, which is positive for ellipses, negative for hyperbolas, and infinite for parabolas; also,
is the semimajor axis, which is positive for ellipses, negative for hyperbolas, and infinite for parabolas; also, ![]() is the pericenter distance of the orbit. The case of
is the pericenter distance of the orbit. The case of ![]() leads to a circular orbit and the simple solution
leads to a circular orbit and the simple solution ![]() (cf., Equation (2a)), so that we will regard
(cf., Equation (2a)), so that we will regard ![]() hereafter in the present work.
hereafter in the present work.
Johannes Kepler announced the relevant laws of above equation early in 1609 and 1619 [4] . He has used physics as a guide in this discovery [5] . For four centuries, the Kepler’s problem is to solve the nonlinear Kepler’s Equation (2) for the eccentric anomaly.
Early analytical solution of Kepler’s equation was considered in a comprehensive study of Tisserand [6] . Recently, analytical works of the solution and use of Kepler’s equation have been proposed by various authors (see, e.g., [7] - [12] ).
In virtually every decade from 1650 to the present, there have appeared papers devoted to the solution of this Kepler’s equation. Its exact analytical solution is unknown, and therefore, efficient procedures to solve it numerically have been well discussed in many standard text books of Celestial Mechanics and Astrodynamics as well as in a large number of papers. Colwell [13] contains extensive references to the Kepler problem in his book. During last two decades, studies were carried out by several investigators of the present problem [2] [14] -[18] . In these studies, they used numerical or approximations methods for solution of the Kepler’s equation. Hence, it appears that an analytical solution of the Kepler’s equation will be of great interest.
In the current study, an analytical investigation of the Kepler’s equation real roots in closed form is presented. In Section 2, we will establish the general form of Kepler’s equation and will clear up the useful identities of the universal functions. In Section 3, using the two-dimensional Laplace transform technique, we will present an analytical solution for the universal Kepler’s equation, obtaining the universal functions ![]() as function of the universal anomaly
as function of the universal anomaly ![]() and the time
and the time![]() . In Section 4, in the first step we will establish one new biquadratic equation for universal anomaly
. In Section 4, in the first step we will establish one new biquadratic equation for universal anomaly ![]() for all conics with the help of Newman’s equation (cf. Equation (23)) and some identities of the new expressions of universal functions. Then, the solution
for all conics with the help of Newman’s equation (cf. Equation (23)) and some identities of the new expressions of universal functions. Then, the solution ![]() of the present problem has been obtained, solving this biquadratic equation for all conics.
of the present problem has been obtained, solving this biquadratic equation for all conics.
Finally, discussion of the results, thus obtained, is presented in Section 5; the new solution of the problem will prove that verifies the traditional form of Kepler’s equations for elliptic, hyperbolic or parabolic orbits. The elliptic, hyperbolic or parabolic Keplerian motion is easily plotted, using this new solution.
2. General Form of Kepler’s Equation
In order to solve the Kepler’s Equation (2), we use here the generalized form of this equation with the universal functions and the universal anomaly instead of the eccentric anomaly (see [3] , Section 4.5).
Working for the Kepler’s Equation (2), we consider an object following a path of same eccentricity ![]() about the center of attracting body; the object is at time
about the center of attracting body; the object is at time ![]() in (vector) position
in (vector) position ![]() with (vector) velocity
with (vector) velocity![]() . The time t is measured from the pericenter passage; so, when
. The time t is measured from the pericenter passage; so, when ![]() this object was at position
this object was at position ![]() (with
(with![]() ) of the pericenter with velocity
) of the pericenter with velocity ![]() (with
(with![]() ) and eccentric anomaly
) and eccentric anomaly![]() . We emphasize that the vectors
. We emphasize that the vectors ![]() and
and ![]() originate at the center of attraction. Then, we introduce the universal anomaly
originate at the center of attraction. Then, we introduce the universal anomaly![]() , which is defined by Sundman transformation:
, which is defined by Sundman transformation:
![]() (3)
(3)
(see [3] , Equation (4.71)) and related to the classical eccentric anomaly by
![]() (4a)
(4a)
![]() (4b)
(4b)
![]() (4c)
(4c)
where E is the eccentric anomaly angle of elliptic or hyperbolic orbit and D the parabolic eccentric anomaly of parabolic orbit with dimension ![]() (see [9] , Equation (18)). The
(see [9] , Equation (18)). The ![]() denotes the reciprocal of the semimajor axis
denotes the reciprocal of the semimajor axis![]() , namely
, namely
![]() (5a,b,c)
(5a,b,c)
Depending on the sign of ![]() or the value of the eccentricity
or the value of the eccentricity![]() , the type of the orbit is determined such that:
, the type of the orbit is determined such that: ![]() (or
(or![]() ) for elliptic orbits;
) for elliptic orbits; ![]() (or
(or![]() ) for hyperbolic orbits and
) for hyperbolic orbits and ![]() (or
(or![]() ) for parabolic orbits. Note that the universal anomaly
) for parabolic orbits. Note that the universal anomaly ![]() is a new independent variable with dimension
is a new independent variable with dimension ![]() (see [3] , Equation (4.70)).
(see [3] , Equation (4.70)).
From the initial condition ![]() and the known relations:
and the known relations:![]() ,
, ![]() for elliptic orbits and
for elliptic orbits and![]() ,
, ![]() for hyperbolic orbits (see [3] , Sections 4.3 and 4.4), we have also for the present problem
for hyperbolic orbits (see [3] , Sections 4.3 and 4.4), we have also for the present problem
![]() (6a,b)
(6a,b)
where ![]() stands for the pericenter distance of the orbit related to the parameter
stands for the pericenter distance of the orbit related to the parameter ![]() with the relation
with the relation
![]() (7)
(7)
Remark that the ![]() is a non-negative parameter and the pericenter distance
is a non-negative parameter and the pericenter distance ![]() may be positive or zero; both of them have dimensions of length (see [3] , Section 4.1).
may be positive or zero; both of them have dimensions of length (see [3] , Section 4.1).
Now, using the universal functions defined by
![]() (8)
(8)
with their following useful properties:
![]() (9a)
(9a)
![]() (9b)
(9b)
![]() (9c)
(9c)
![]() (9d)
(9d)
(see [3] , Equation (9.73)), the two forms of Kepler’s Equation (2) are incorporated in one universal equation
![]() (10)
(10)
which is a standard form of the traditional Kepler’s Equations (2) with the epoch at pericenter passage (see [9] , Equation (23) and [2] , Equation (29)). The general formula (10) is valid for all values of ![]() and
and![]() ; in particular, it is good for parabolic orbits where
; in particular, it is good for parabolic orbits where![]() .
.
To find out the expression of many orbital quantities, e.g. the magnitude of the position vector![]() , we must solve the standard universal form (10) of the Kepler’s equation for the universal anomaly as function of the time, namely
, we must solve the standard universal form (10) of the Kepler’s equation for the universal anomaly as function of the time, namely![]() .
.
3. Solution of the Universal Kepler’s Equation
In order to obtain the analytical solution of the present problem, we shall solve first the universal Kepler’s equation Equation (10), obtaining the universal functions![]() ,
, ![]() as a function of the universal anomaly and the time. For this purpose, we will use the double Laplace transformation technique, which was analytically studied by Aghili and Salkhordeh-Moghaddam [19] and by Valkó and Abate [20] .
as a function of the universal anomaly and the time. For this purpose, we will use the double Laplace transformation technique, which was analytically studied by Aghili and Salkhordeh-Moghaddam [19] and by Valkó and Abate [20] .
The universal functions![]() : For this case, we introduce a new variable
: For this case, we introduce a new variable ![]() so that
so that
![]() (11a)
(11a)
![]() (11b)
(11b)
![]() (11c)
(11c)
(see Equations (9)) and the universal Kepler’s Equation (10) becomes
![]() (12a)
(12a)
From the initial condition ![]() or
or ![]() and Equation (9a), we have the corresponding initial conditions to the Equation (12a)
and Equation (9a), we have the corresponding initial conditions to the Equation (12a)
![]() (12b)
(12b)
The application of double Laplace transform (with respect to ![]() and
and![]() ) to the Equations (12) gives the solution
) to the Equations (12) gives the solution ![]() in transform domain as
in transform domain as
![]() (13)
(13)
where ![]() and
and ![]() are the transform variables of
are the transform variables of ![]() and time
and time![]() , respectively. For the solution of partial differential Equation (12a), we use the Appendix.
, respectively. For the solution of partial differential Equation (12a), we use the Appendix.
Now, the universal function ![]() can be obtained by taking the inverse transform of Equation (13) (cf., Appendix). So, we get
can be obtained by taking the inverse transform of Equation (13) (cf., Appendix). So, we get
![]() (14)
(14)
where we have abbreviated
![]() (15)
(15)
with dimensions:![]() .
.
The universal functions![]() : For this case, we will use a new variable
: For this case, we will use a new variable ![]() so that
so that
![]() (16a)
(16a)
![]() (16b)
(16b)
![]() (16c)
(16c)
(see Equations (9c)) and the universal Kepler’s Equation (10) becomes
![]() (17a)
(17a)
For ![]() or
or ![]() and Equation (9a), we have the initial conditions to the Equation (17a)
and Equation (9a), we have the initial conditions to the Equation (17a)
![]() (17b)
(17b)
Similarly as in the case of![]() , using the double Laplace transform (with respect to
, using the double Laplace transform (with respect to ![]() and
and![]() ) for the Equations (17), we obtained the solution
) for the Equations (17), we obtained the solution ![]() in transform domain as
in transform domain as
![]() (18)
(18)
(cf., Appendix). Inverting ![]() we have the universal function
we have the universal function ![]()
![]() (19)
(19)
where we have defined the non-dimensional function
![]() (20)
(20)
Then, substituting the results of Equation (14) and (19) into the relations ![]() and
and ![]() (cf., Equation (9b)), respectively, we can easily obtain the new universal functions
(cf., Equation (9b)), respectively, we can easily obtain the new universal functions ![]() and
and ![]() as
as
![]() (21)
(21)
![]() (22)
(22)
where ![]() and
and ![]() are given from Equations (15) and (20), respectively.
are given from Equations (15) and (20), respectively.
4. Analytical Solution of the Problem
In order to obtain a solution for the universal anomaly![]() , we use the explicit expression for
, we use the explicit expression for![]() :
:
![]() (23)
(23)
where![]() . This relation was discovered by C. M. Newman and its
. This relation was discovered by C. M. Newman and its ![]() does not involve any of the universal functions
does not involve any of the universal functions ![]() (see [3] , Equation (4.86)). The
(see [3] , Equation (4.86)). The ![]() can be also given by the known equation (see [3] , Equation (4.83))
can be also given by the known equation (see [3] , Equation (4.83))
![]() (24)
(24)
Substituting Equation (24) (with ![]() given by (21)) into Equation (23), the following relation is obtained
given by (21)) into Equation (23), the following relation is obtained
![]() (25)
(25)
To find out two more relations between![]() ,
, ![]() and
and![]() , similar to Equation (25), we will use the basic relation
, similar to Equation (25), we will use the basic relation ![]() and the definitions of
and the definitions of ![]() and
and ![]() Equations (15) and (20), respectively. Thus, we can easily obtain the relation
Equations (15) and (20), respectively. Thus, we can easily obtain the relation
![]() (26)
(26)
Further, we can find one more relation using the basic identity ![]() (see [3] , Equation (4.93)); indeed, with the help of Equations (14), (21) and (22), we obtain the relation
(see [3] , Equation (4.93)); indeed, with the help of Equations (14), (21) and (22), we obtain the relation
![]() (27)
(27)
The three Equations (25), (26) and (27) are a system of the three unknowns:![]() ,
, ![]() and
and![]() . Solving this system, we get from two Equations (25) and (26) the following relations
. Solving this system, we get from two Equations (25) and (26) the following relations
![]() (28a)
(28a)
![]() (28b)
(28b)
Finally, substituting Equations (28) into Equation (27), we obtain the following biquadratic equation for universal anomaly ![]()
![]() (29)
(29)
where we have abbreviated
![]() (30a)
(30a)
![]() (30b)
(30b)
![]() (30c)
(30c)
with dimensions:![]() ,
, ![]() and
and![]() .
.
The solution of the biquadratic Equation (29) gives the relation between the universal anomaly ![]() and the time
and the time ![]() for all conics: ellipse, hyperbola or parabola. The solution of this equation can be obtained using the standard formula of the solution for biquadratic equation.
for all conics: ellipse, hyperbola or parabola. The solution of this equation can be obtained using the standard formula of the solution for biquadratic equation.
Solving the new biquadratic Equation (29), we get the solution of the present problem for the universal anomaly ![]() at time
at time ![]() as shown below
as shown below
![]() (31)
(31)
where we have abbreviated
![]() (32a)
(32a)
particularly, for elliptic orbits ![]() we have
we have
![]() (32b)
(32b)
for hyperbolic orbits ![]()
![]() (32c)
(32c)
and for parabolic orbits ![]()
![]() (32d)
(32d)
Remark that the discriminant of the biquadratic Equation (29) is![]() , for
, for![]() . Consequently, the solution (31) is real in the cases of hyperbolic and parabolic cases since the corresponding
. Consequently, the solution (31) is real in the cases of hyperbolic and parabolic cases since the corresponding![]() , given from Equations (32c,d), are always real-valued. In the case of the elliptic Keplerian orbits, the Equation (31) is real only in the special case for which
, given from Equations (32c,d), are always real-valued. In the case of the elliptic Keplerian orbits, the Equation (31) is real only in the special case for which![]() , given from Equation (32b), becomes real, namely for the case
, given from Equation (32b), becomes real, namely for the case
![]() (32e,f)
(32e,f)
where ![]() is the mean anomaly defined by Equation (2c). The upper limit of this mean anomaly
is the mean anomaly defined by Equation (2c). The upper limit of this mean anomaly ![]() is defined from the relation (32f) for every completed trip of the orbiting body in its elliptic orbit about the center of the attracting body; this limit is useful for determination of each Keplerian ellipse (cf., the applications in the next section).
is defined from the relation (32f) for every completed trip of the orbiting body in its elliptic orbit about the center of the attracting body; this limit is useful for determination of each Keplerian ellipse (cf., the applications in the next section).
In the case of parabolic orbits where the limiting case ![]() (or
(or![]() ) and
) and ![]() corresponds to
corresponds to ![]() and
and![]() , the equation (29) and its solution (31) are reduced to
, the equation (29) and its solution (31) are reduced to
![]() (33a)
(33a)
![]() (33b)
(33b)
The Equation (31) is the solution of the present problem for all conics (ellipse, hyperbola or parabola) and expresses the relation between the universal anomaly ![]() and the time t.
and the time t.
Knowing the solution of the universal anomaly![]() , we establish the exact expressions of the universal functions
, we establish the exact expressions of the universal functions![]() , n = 0, 1, 2, 3 as functions of the time
, n = 0, 1, 2, 3 as functions of the time![]() . Indeed, using Equation (31), the Equation (28) are obtained as functions of the time
. Indeed, using Equation (31), the Equation (28) are obtained as functions of the time![]() :
:
![]() (34a)
(34a)
![]() (34b)
(34b)
Then, the universal functions (19), (14), (21) and (22) are expressed as functions of the time t as show below
![]() (35a)
(35a)
![]() (35b)
(35b)
![]() (35c)
(35c)
![]() (35d)
(35d)
The magnitude of the position vector ![]() of the orbiting body is
of the orbiting body is
![]() (36a,b)
(36a,b)
(see [3] , Equation (4.82) and [14] , Equation (8)). Substituting into Equation (36b) the new expressions of![]() , given by Equation (35b), we obtain the time-dependent distance
, given by Equation (35b), we obtain the time-dependent distance ![]() of the orbiting body from the center of attraction as
of the orbiting body from the center of attraction as
![]() (37)
(37)
Furthermore, if we work in the orbital reference system with the origin at the attracting center (or focus), we chose the ![]() plane to be the plane of motion with
plane to be the plane of motion with ![]() -axis pointing toward pericenter and
-axis pointing toward pericenter and ![]() -axis in the direction for which the true anomaly
-axis in the direction for which the true anomaly ![]() is 90˚; in this way the
is 90˚; in this way the ![]() -axis is parallel to the angular momentum. Then, if
-axis is parallel to the angular momentum. Then, if ![]() and
and ![]() are the coordinates of a point
are the coordinates of a point ![]() on the conic orbit, we have
on the conic orbit, we have ![]() and
and
![]() (38)
(38)
where ![]() is the non-negative quantity given by Equation (7) (see [3] , Equation (4.3)). Thus, the
is the non-negative quantity given by Equation (7) (see [3] , Equation (4.3)). Thus, the ![]() and
and ![]() coordinates can be expressed as function of the time
coordinates can be expressed as function of the time![]() , using Equations (38) and the identities:
, using Equations (38) and the identities:![]() ,
,![]() ; namely, we get
; namely, we get
![]() (39a)
(39a)
![]() (39b)
(39b)
where ![]() and
and ![]() are given from Equations (35) (see [14] , Equations (6)-(7)).
are given from Equations (35) (see [14] , Equations (6)-(7)).
5. Discussion
Using the standard form of the universal Kepler’s equation (10) with the epoch at pericenter passage, we have derived a new biquadratic equation (29) for universal anomaly ![]() as a function of the time
as a function of the time![]() . This equation governs the motion of an orbiting body following a path with position vector
. This equation governs the motion of an orbiting body following a path with position vector ![]() from the center of attracting body and with velocity vector
from the center of attracting body and with velocity vector![]() .
.
The new solution (31) of the present problem was obtained solving Equation (29) with initial-value conditions for the orbiting body at time ![]() passages from the pericenter, with minimum position vector
passages from the pericenter, with minimum position vector![]() , velocity vector
, velocity vector ![]() and eccentric anomaly
and eccentric anomaly![]() .
.
The solution (31) is a solution of the present problem. Indeed, the new expressions of the universal functions![]() , and
, and ![]() given by (35a,c) verify universal Kepler’s Equation (10). Moreover, the solution (31) is a solution of the Equation (29), since it can be easily verified by substitution of (31) into (29).
given by (35a,c) verify universal Kepler’s Equation (10). Moreover, the solution (31) is a solution of the Equation (29), since it can be easily verified by substitution of (31) into (29).
The solution (31) verifies also the traditional forms of Kepler’s Equation (2). Particularly, in the case of elliptic orbits ![]() the solution (31) of the problem is reduced for the eccentric anomaly (cf. Equation (4a)) to the form
the solution (31) of the problem is reduced for the eccentric anomaly (cf. Equation (4a)) to the form
![]() (40)
(40)
where ![]() is the mean anomaly given by Equation (2c) and
is the mean anomaly given by Equation (2c) and
![]() (41)
(41)
Note that ![]() and
and ![]() (cf. Equation (32f)) for
(cf. Equation (32f)) for![]() .
.
Similarly, in the case of hyperbolic orbits ![]() the solution (31) of the problem is reduced, for the eccentric anomaly (cf. Equation (4b)), to
the solution (31) of the problem is reduced, for the eccentric anomaly (cf. Equation (4b)), to
![]() (42)
(42)
where ![]() is the mean anomaly given by Equation (2d) and
is the mean anomaly given by Equation (2d) and
![]() (43)
(43)
Finally, in the case of parabolic orbits ![]() the solution (33b) gives for the parabolic eccentric anomaly (cf. Equations (4c) and (2e)):
the solution (33b) gives for the parabolic eccentric anomaly (cf. Equations (4c) and (2e)):
![]() (44)
(44)
From the other hand, the standard and hyperbolic trigonometric functions of Equations (2) are expressed as
![]() (45a)
(45a)
![]() (45b)
(45b)
where we have use Equation (35) and the relationship between the function U1 and the standard and hyperbolic
trigonometric functions of Equations (2): ![]() and
and ![]() for ellipse
for ellipse
and hyperbola, respectively (see [3] , Problem 4 - 21 and [9] , Equation (24)).
Now, we will prove that the Equations (40) and (42) represent the solutions of the traditional forms of Kepler’s Equations (2). Indeed, it can be shown that the left-hand sides of Equations (2) are reduced to the right- hand sides, namely
![]() (46a)
(46a)
![]() (46b)
(46b)
in accordance with the Equations (40), (42) and (45).
It should be pointed out that our solutions for eccentric anomaly (cf., Equations (40) and (42)) are ready for physical applications in the corresponding Keplerian orbits.
In addition to above Keplerian orbits, the new solution (33b) of the present problem for the case of parabola (![]() and
and![]() ) verifies the traditional Barker’s equation for parabolic orbits
) verifies the traditional Barker’s equation for parabolic orbits
![]() (47)
(47)
Remark that the parabolic Keplerian equation is called Barker’s equation (see [3] , Equation (4.24)). Indeed, from the definition (8) for the universal functions we have ![]() and
and![]() . Using the solution (33b), these universal functions are expressed from Equations (35a,c), so that
. Using the solution (33b), these universal functions are expressed from Equations (35a,c), so that
![]() (48a,b)
(48a,b)
where ![]() is given from Equation (32d). Then, the left-hand side of Equations (47) is reduced to the right- hand side, namely
is given from Equation (32d). Then, the left-hand side of Equations (47) is reduced to the right- hand side, namely
![]() (49)
(49)
In order to study the Keplerian orbits with the help of the new solutions, we use also the cartesian coordinates ![]() and
and ![]() with the origin at the center of the ellipse or hyperbola. In this case the
with the origin at the center of the ellipse or hyperbola. In this case the ![]() and
and ![]() coordinates of the orbital
coordinates of the orbital ![]() plane system given by Equations (39) are related to the system
plane system given by Equations (39) are related to the system ![]() with the relations
with the relations ![]() and
and ![]() (see [3] , Equation (4.4)); so, for the case
(see [3] , Equation (4.4)); so, for the case![]() , these new coordinates can be obtained in the explicit forms
, these new coordinates can be obtained in the explicit forms
![]() (50a)
(50a)
![]() (50b)
(50b)
where we have defined the non-dimensional relation
![]() (51)
(51)
in accordance to the Equations (39). Then, we introduce the non-dimensional coordinates
![]() (52a)
(52a)
![]() (52b)
(52b)
The new expressions (52) verify the following equations of ellipse ![]() and hyperbola
and hyperbola![]() , respectively:
, respectively:
![]() (53a)
(53a)
![]() (53b)
(53b)
where ![]() is defined by Equation (51). Remark that the equations (53) are the non-dimensional forms of the ellipse and hyperbola, respectively, in the cartesian system
is defined by Equation (51). Remark that the equations (53) are the non-dimensional forms of the ellipse and hyperbola, respectively, in the cartesian system ![]() with the origin at the center of the ellipse or hyperbola (see [1] , Equations (A.2.1) and (A.4.2)).
with the origin at the center of the ellipse or hyperbola (see [1] , Equations (A.2.1) and (A.4.2)).
In the other hand, for the case of parabola![]() , the coordinates
, the coordinates ![]() and
and ![]() can be also obtained, from Equations (39), as following
can be also obtained, from Equations (39), as following
![]() (54a)
(54a)
![]() (54b)
(54b)
Then, we have, from Equations (54),
![]() (55a,b)
(55a,b)
The last Equation (55) is the equation of parabola, which passes through its pericenter with coordinates ![]()
(see [3] , Equation (3.22)). The non-dimensional form of Equation (55) is
![]() (56)
(56)
with the non-dimensional coordinates
![]() (57a,b)
(57a,b)
In addition to above results for the non-dimensional coordinates we have (for physical application) the corresponding expressions:
For elliptic orbits ![]() the Equation (51) becomes
the Equation (51) becomes
![]() (58a)
(58a)
for hyperbolic orbits ![]() the Equation (51) becomes
the Equation (51) becomes
![]() (58b)
(58b)
for parabolic orbits ![]() the Equation (57a) yields
the Equation (57a) yields
![]() (58c)
(58c)
where![]() ,
, ![]() and
and ![]() are the mean anomalies of ellipse, hyperbola and parabola, respectively (cf., Equations (2c,d,e)). These mean anomalies can be varied from 0 to
are the mean anomalies of ellipse, hyperbola and parabola, respectively (cf., Equations (2c,d,e)). These mean anomalies can be varied from 0 to![]() , where
, where ![]() is an integer. Note that the non- dimensional coordinates of attractive center (or focus)
is an integer. Note that the non- dimensional coordinates of attractive center (or focus) ![]() in the non-dimensional cartesian system
in the non-dimensional cartesian system ![]() is given by
is given by ![]() for all Keplerian orbits (ellipse, hyperbola or parabola).
for all Keplerian orbits (ellipse, hyperbola or parabola).
In order to get a physical insight into the new solution of the Kepler’s problem, we apply the above results for the system Earth-Moon. For this system the eccentricity of the Moon is ![]() and the upper limit for the mean anomaly can be obtained from relation (32f) as
and the upper limit for the mean anomaly can be obtained from relation (32f) as![]() . So, varying the mean anomaly
. So, varying the mean anomaly ![]() (with
(with![]() ) and using Equations (58a) and (52b), the elliptic Keplerian motion of the Moon about the Earth can be easily plotted in the non-dimensional cartesian system
) and using Equations (58a) and (52b), the elliptic Keplerian motion of the Moon about the Earth can be easily plotted in the non-dimensional cartesian system ![]() (Figure 1). Remark that the non-dimen- sional coordinates of the Earth are obtained as
(Figure 1). Remark that the non-dimen- sional coordinates of the Earth are obtained as![]() .
.
Note that the use of the upper limit of the mean anomaly, given from the relation ![]() (cf. relation (32f)), is import for the plotting of all elliptic Keplerian orbits. To confirm that we give two more examples: (a) We consider an object following an elliptic orbit with eccentricity
(cf. relation (32f)), is import for the plotting of all elliptic Keplerian orbits. To confirm that we give two more examples: (a) We consider an object following an elliptic orbit with eccentricity ![]() about the center of attracting body; the upper limit of the mean anomaly, from relation (32f), is
about the center of attracting body; the upper limit of the mean anomaly, from relation (32f), is![]() ; then, varying the mean anomaly
; then, varying the mean anomaly ![]() (with
(with![]() ) and using Equations (58a) and (52b), we plot the elliptic Keplerian orbit in the non-dimensional cartesian system
) and using Equations (58a) and (52b), we plot the elliptic Keplerian orbit in the non-dimensional cartesian system ![]() (Figure 2). (b) We consider another object in an elliptic orbit with
(Figure 2). (b) We consider another object in an elliptic orbit with
![]()
Figure 1. The elliptic orbit of the Moon ![]() about the Earth.
about the Earth.
![]()
Figure 2. Two elliptic Keplerian orbits with eccentricities ![]() and
and![]() .
.
eccentricity ![]() about the center of another attracting body; the upper limit of the new mean anomaly, from relation (32f), is
about the center of another attracting body; the upper limit of the new mean anomaly, from relation (32f), is![]() ; and, varying the mean anomaly
; and, varying the mean anomaly ![]() (with
(with![]() ), we plot the elliptic Keplerian orbit in the non-dimensional cartesian system
), we plot the elliptic Keplerian orbit in the non-dimensional cartesian system ![]() (Figure 2).
(Figure 2).
Now, varying the mean anomaly ![]() (with
(with ![]() for the present plot) and using equations (58b) and
for the present plot) and using equations (58b) and
![]() (cf., Equation (52b), we plot of the hyperbolic Keplerian motion of an orbiting body
(cf., Equation (52b), we plot of the hyperbolic Keplerian motion of an orbiting body
with the eccentricity ![]() about the attractive center
about the attractive center ![]() (Figure 3).
(Figure 3).
Finally, varying the mean anomaly ![]() (with
(with ![]() for the present plot) and using Equations (58c), and (56), we plot of the parabolic Keplerian motion of an orbiting body with the eccentricity
for the present plot) and using Equations (58c), and (56), we plot of the parabolic Keplerian motion of an orbiting body with the eccentricity ![]() about the attractive center
about the attractive center ![]() (Figure 4).
(Figure 4).
6. Conclusions
This work presents a solution to the well known Keplerian two body physical problem. From the investigation
![]()
Figure 3. The hyperbola of an orbiting body (with![]() ) about the attractive centre
) about the attractive centre![]() .
.
![]()
Figure 4. The parabola of an orbiting body (with![]() ) about the attractive centre
) about the attractive centre![]() .
.
for this new solution, the main conclusions have been drawn as following:
1) An analytical solution for the universal Kepler’s equation has been determined, obtaining the universal functions![]() , n = 0, 1, 2, 3 as function of the universal anomaly
, n = 0, 1, 2, 3 as function of the universal anomaly ![]() and the time
and the time ![]() with the help of the two-dimensional Laplace transform technique.
with the help of the two-dimensional Laplace transform technique.
2) Using an explicit expression for the universal anomaly ![]() without any of the
without any of the ![]() functions (cf., Equation (23)) and some identities of the new obtained universal functions, we developed a biquadratic equation for universal anomaly
functions (cf., Equation (23)) and some identities of the new obtained universal functions, we developed a biquadratic equation for universal anomaly ![]() for all conics: ellipse, hyperbola or parabola.
for all conics: ellipse, hyperbola or parabola.
3) The solution ![]() of the present problem has been obtained, solving this biquadratic equation for all conics.
of the present problem has been obtained, solving this biquadratic equation for all conics.
4) This new analytical solution for the universal anomaly has been discussed and proved that verifies the universal Kepler’s equation (cf., Equation (10)), since the time depended universal functions U3 and U1 verify this equation. Then, the solutions for the eccentric anomaly (cf., Equations (40) and (42)) were also proved that verify the traditional form of Kepler’s equations for elliptic or hyperbolic orbits. This new solution for the universal anomaly has also proved that verifies the traditional Barker’s equation for parabolic orbits [11] . The elliptic, hyperbolic or parabolic Keplerian motion is plotted, using this analytical solution.
5) To our knowledge, this work gives in closed form the actual analytical solution of the Kepler’s problem. The advantage of the new solution is simple and ready for physical applications in the elliptic, hyperbolic or parabolic Keplerian orbits.
Appendix
Solution of partial differential equations using two-dimensional Laplace transforms
The general form of second-order linear partial differential equation in two variables is given as following
![]() (A1)
(A1)
where ![]() are constants and
are constants and ![]() is source function of
is source function of ![]() and
and ![]() or constant. We use also the abbreviations for the initial conditions
or constant. We use also the abbreviations for the initial conditions
![]() (A2)
(A2)
and their one-dimensional Laplace transformations![]() ,
, ![]() ,
, ![]() and
and![]() , where “
, where “![]() ” and “
” and “![]() ” the transform variables of
” the transform variables of ![]() and
and![]() , respectively (see [19] and [21] for details). Then, we get the relations for two-dimensional Laplace transforms
, respectively (see [19] and [21] for details). Then, we get the relations for two-dimensional Laplace transforms
![]() (A3a)
(A3a)
![]() (A3b)
(A3b)
![]() (A3c)
(A3c)
![]() (A3d)
(A3d)
![]() (A3e)
(A3e)
![]() (A3f)
(A3f)
![]() (A3g)
(A3g)
![]() (A3h)
(A3h)
![]() (A3i)
(A3i)
in accordance with the two-dimensional analysis formula, which can be written as one-dimensional analysis in the ![]() direction followed by one-dimensional analysis in the
direction followed by one-dimensional analysis in the ![]() direction:
direction:
![]() (A4)
(A4)
Now, applying double Laplace transformation to both sides of Equation (A1) and using Equations (A3), we obtain the solution of Equation (A1) in the transform domain as
![]() (A5a)
(A5a)
with the abbreviation
![]() (A5b)
(A5b)
In order to invert this two-dimensional Laplace transform![]() , we follow the double inversion as a two- step process [20] . In the first step we invert, say, on the “
, we follow the double inversion as a two- step process [20] . In the first step we invert, say, on the “![]() ” transform variable
” transform variable
![]() (A6)
(A6)
where we keep the second transform variable ![]() as a constant. In the second step we invert on the “
as a constant. In the second step we invert on the “![]() ” transform variable and obtain, finally,
” transform variable and obtain, finally,
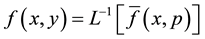
(A7)