Comparison of Simulation Methods of Ion-Atomic Collisions in PIC-MC ()
1. Introduction
The simulation of plasma by Particle-in-Cell Monte-Carlo (PIC-MC) method has received widespread application in calculations of ion current on probe and dust particle and plasma simulation of glow and high-frequency discharges [1] - [6] . The important stage in PIC-MC method is simulation of ion collisions with neutral atoms. It includes interval simulation between collisions, simulation of velocity and direction of ion motion after collision.
The drift time of an ion up to the next collision has probabilistic nature: probability of collisions for the time
 doesn’t depend on the previous way and proportional to
doesn’t depend on the previous way and proportional to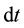 :
: ,
, ―concentration of atoms,
―concentration of atoms,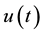 ―relative velocity ion-atom,
―relative velocity ion-atom, ―cross-section of collision.
―cross-section of collision.
Let us assume by this ―probability of absence of collision for the time
―probability of absence of collision for the time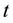 . Then the probability of collision for
. Then the probability of collision for  after non-collision time
after non-collision time , determining decrease of
, determining decrease of  as
as  increases to
increases to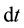 , is
, is
 ,
,
where  is probability density. Equations (1) are the expressions for probability of absence of collision for the time
is probability density. Equations (1) are the expressions for probability of absence of collision for the time  and for probability density
and for probability density
![]() (1)
(1)
Equation (2) is probability of collision since the time ![]() is:
is:
![]() (2)
(2)
The following methods of simulation of the interval between collisions are applied.
2. Review of Methods of Simulation of the Interval between Collisions
2.1. Constant Time between Collisions [7] - [9]
Equation (3) is approximation of constant time between collisions
![]() (3)
(3)
This approximation is correct at inverse dependence of cross-section on velocity.
In the supposition based on Equation (3) ![]() Simulation of the random value “
Simulation of the random value “![]() ” is done
” is done
with the help of uniformly distributed at [0,1] random value “rand”. Equation (4) shows the expression for random value “rand”
![]() (4)
(4)
In Equation (4) ![]() is replaced with
is replaced with![]() , as it is the random value as well.
, as it is the random value as well.
2.2. Constant Path Length [5] [6] [9] [10]
Equation (5) is the expression for path length in this case
![]() (5)
(5)
Let us replace a variable in Equation (1)![]() , then taking into account Equation (5) we will get Equation (6):
, then taking into account Equation (5) we will get Equation (6):
![]() (6)
(6)
For each ion path length is simulated after each collision. Equations (7) are the expressions for ion’s path length
![]() (7)
(7)
The achievement of individual path length by each ion is checked by summing up its ways on each time step![]()
The approximation of constant path length takes into account the change of ion velocity, however the cross- section of collisions is considered to be constant here that can be accepted with some approximation at resonant charge exchange. In [9] a problem of the method considered has been revealed. If the method of constant path length was used, the decrease of average ion energy was observed because of more frequent collisions of fast ions transferring energy to atoms and absence of direct Maxwellian process among charged particles in PIC.
2.3. Simulation of Collision Probability on Each Time Step [1] [3] [11]
For the time interval ![]() relative velocity and cross-section are considered to be constant. Equation (8) is probability of collision for the time
relative velocity and cross-section are considered to be constant. Equation (8) is probability of collision for the time![]() :
:
![]() (8)
(8)
While each ion is simulated, if ![]() the collision occurs. Values
the collision occurs. Values ![]() and
and ![]() cor-
cor-
respond to the current time point![]() . This method demands significant increase of computing time that makes it hardly applicable to large ensembles of particles.
. This method demands significant increase of computing time that makes it hardly applicable to large ensembles of particles.
2.4. “Null-Collision” Algorithm
This algorithm is considered in details in [2] and actively used [2] [4] [12] . At first, the maximum value of
product ![]() on the whole range of all possible relative ion-atom velocities is determined (or appointed). Upon the value
on the whole range of all possible relative ion-atom velocities is determined (or appointed). Upon the value ![]() the constant conditional collision probability for the time
the constant conditional collision probability for the time ![]() is calculated. Equa-
is calculated. Equa-
tion (9) is constant conditional collision probability for the time ![]()
![]() . (9)
. (9)
Then, in case of total number of ions N on each time step, the number of ion is simulated P0N times. For this ion rand is simulated again and the type of collision or the absence of it is defined. Equation (10) is the condition of event that k-type of collision occurs:
![]() (10)
(10)
At ![]() collision doesn’t occur. It compensates for the randomness of choice
collision doesn’t occur. It compensates for the randomness of choice![]() .
.
Treatment methods of collision probability are combined in the “null-collision” technique. At first, the number of the ion is determined in the ensemble, and then the type of collision or its absence is defined through the change of ion state in time. The number of arithmetic operations ![]() times is smaller than in the method of determination of collision probability on each time step.
times is smaller than in the method of determination of collision probability on each time step.
In [12] “null-collision” method is applied to define the collision probability on each time step. At ![]()
![]() is simulated and, if
is simulated and, if ![]() the collision doesn’t occur, and it occurs in the opposite case.
the collision doesn’t occur, and it occurs in the opposite case.
There is a variety of revisions of the “null-collision” algorithm used for simulation of electron-atom collisions when cross-sections are strongly dependent on electrons’ energy. Thus, in the method of constant time between
collisions the time interval is determined by maximum possible value of ![]() [13] . Individual time interval is simulated for each electron
[13] . Individual time interval is simulated for each electron ![]() and when this value is achieved then the event of collision should be treated by generation a new rand. If
and when this value is achieved then the event of collision should be treated by generation a new rand. If ![]() then the collision takes place, otherwise the absence of collision is assumed.
then the collision takes place, otherwise the absence of collision is assumed.
3. Improvement of Methods and Simulation Experiment
3.1. Improvement of Methods of Constant Path Lengths and Time between Collisions―The Method of Accumulation of Probability
It is possible to offer the following method taking into account the change of value ![]() on the ion path. Let us consider expression for density of probability by Equation (1). If according to Equation (11) new variable is introduced
on the ion path. Let us consider expression for density of probability by Equation (1). If according to Equation (11) new variable is introduced
![]() (11)
(11)
then we will have ![]() for density of probability. Equation (12) is collision probability for the time
for density of probability. Equation (12) is collision probability for the time![]() :
:
![]() (12)
(12)
Equations (13) are the expressions if individual ion is simulated:
![]() (13)
(13)
Summing up by steps in time lasts up to the reaching of equality in Equation (13). In such a way, this algorithm takes into account the change of ![]() as well as the change of
as well as the change of ![]() and
and![]() , having approximately the same number of arithmetic operations. At the same time, unlike in the “null-collision” method, both the probability of collision and change of particles’ state which determines this probability are taken into consideration for each particle independently in time. According to the algorithm features it is natural to call this technique “the method of accumulation of probability”.
, having approximately the same number of arithmetic operations. At the same time, unlike in the “null-collision” method, both the probability of collision and change of particles’ state which determines this probability are taken into consideration for each particle independently in time. According to the algorithm features it is natural to call this technique “the method of accumulation of probability”.
3.2. Simulation of Energy and Direction of Ion Motion after the Collision
Direction of ion motion after the collision is characterized by taking into account deviation from original direction ![]() and azimuth angle
and azimuth angle![]() . Angle
. Angle ![]() is equiprobable at symmetrical atoms
is equiprobable at symmetrical atoms![]() . In the process of recharge ion velocities after collision are usually taken as equal to atomic ones with Maxwell distribution function [1] [2] [5] [6] [10] . Equation (14) is the expression simulation of
. In the process of recharge ion velocities after collision are usually taken as equal to atomic ones with Maxwell distribution function [1] [2] [5] [6] [10] . Equation (14) is the expression simulation of ![]() in this case
in this case
![]() (14)
(14)
At elastic scattering of ion on atom in these works scattering goes only forward. Equation (15) is the formula for ![]() in this case:
in this case:
![]() (15)
(15)
Equation (16) is energy after scattering:
![]() (16)
(16)
In works [11] [14] at elastic collisions the law of ion-atom interaction is stated. Impact parameter and relative velocity are simulated by randomizer and then depending on the minimal radius of approximation the angles and ion energies are calculated after collision. This method makes simulation process significantly more difficult. At the same time Equations (15), (16) don’t take into account the transfer of energy from atoms to ions that is the most significant at weak fields.
Let us consider Monte-Carlo algorithm of simulation of elastic ion-atom collisions on the model of elastic spheres. In this model in Figure 1 normal and tangential components of ions’ velocity after collision are:
![]() ;
;![]() , where
, where ![]() and
and ![]() are weights of ion and atom, correspondingly.
are weights of ion and atom, correspondingly.
Further we consider ion motion in their own gas![]() , then
, then![]() . Angles
. Angles ![]() and
and![]() ―original angles
―original angles
of ion and atom velocities to normal. For the angle ![]() we have:
we have:![]() , where
, where![]() ―target pa-
―target pa-
rameter,![]() ―diameter of spheres. We have equal probability of the azimuth angle. Equation (17) is simulation formula for the azimuth angle:
―diameter of spheres. We have equal probability of the azimuth angle. Equation (17) is simulation formula for the azimuth angle:
![]() . (17)
. (17)
For the density of probability we have![]() , where
, where ![]() then
then ![]() . There from one can deduce Equation (18)
. There from one can deduce Equation (18)
![]() . (18)
. (18)
For strong fields if we ignore atom velocity![]() ,
, ![]() we get
we get![]() ;
; ![]() ;
;![]() , it corresponds to Equations (15), (16) taking into account that
, it corresponds to Equations (15), (16) taking into account that ![]() is the same random value like
is the same random value like![]() .
.
However, in weak fields an ion can get significant additional velocity from an atom in collisions.
Equation (19) is ions’ velocity after collision in this case
![]() , (19)
, (19)
![]() ,
,![]() . Equation (20) is the result for
. Equation (20) is the result for ![]() taking into account that
taking into account that![]() :
:
![]() . (20)
. (20)
Let us consider atom ![]() simulation. Equation (21) is the absolute velocity Maxwell distribution function:
simulation. Equation (21) is the absolute velocity Maxwell distribution function:
![]() (21)
(21)
Equation (20) is the expression for simulation after introducing the new parameter ![]()
![]() (22)
(22)
The integral can be replaced by an analytic expression, having approximation with accuracy up to 3%. Equation (23) is the approximation for ![]()
![]() (23)
(23)
The results of calculations presented in Table 1 reveal the approximation (23) to be close to the exact values.
Equation (24) is density of probability of ![]() angles and azimuth angle
angles and azimuth angle![]() :
:
![]() (24)
(24)
It determines![]() ;
;![]() .
.
Angle ![]() determines the ion deviation from its direction before collision. To determine the ion current in the given direction (along the field) it is necessary to know the angle to this direction (angle
determines the ion deviation from its direction before collision. To determine the ion current in the given direction (along the field) it is necessary to know the angle to this direction (angle ![]() in Figure 2).
in Figure 2).
Let us have angle ![]() to the axis х up to the collision,
to the axis х up to the collision, ![]() and
and ![]() are angles of scattering. Equation (25) is the expression for
are angles of scattering. Equation (25) is the expression for![]() :
:
![]() (25)
(25)
![]()
It is here that we need angle ![]() according to Equation (17).
according to Equation (17).
At resonant charge exchange angle ![]() is simulated immediately. Equations (26) are the formulae in this case
is simulated immediately. Equations (26) are the formulae in this case
![]() (26)
(26)
3.3. Simulation Experiment
To compare “null-collision” method and method of accumulation of probability the simulation experiment of ion motion in constant electric field ![]() in approximation to elastic spheres was carried out. The motion with the charge exchange on atoms and elastic interaction was considered separately.
in approximation to elastic spheres was carried out. The motion with the charge exchange on atoms and elastic interaction was considered separately.
![]()
Figure 2. Angles of ion deviation:![]() ―to the direction up to the collision,
―to the direction up to the collision,![]() ―to the direction of the electric field.
―to the direction of the electric field.
![]()
Table 1. Comparison of approximated ![]() and exact
and exact ![]() values.
values.
The number of ions was taken as equal to 105. Original ion velocities had Maxwell distribution with the temperature of atoms by Equations (23) and (24). The interval of time ![]() at integrating motion equations is chosen depending on the probability of collision for
at integrating motion equations is chosen depending on the probability of collision for ![]() according to Equation (9) within
according to Equation (9) within ![]() Value
Value ![]() was accepted in the range of (2 - 20) values, achieved between collisions for the average time. At the same time change
was accepted in the range of (2 - 20) values, achieved between collisions for the average time. At the same time change ![]() in the given range practically didn’t influence the average drift velocity. Value
in the given range practically didn’t influence the average drift velocity. Value ![]() was taken as constant. Collision process was simulated according to Equations (17)-(26).
was taken as constant. Collision process was simulated according to Equations (17)-(26).
Equations (27) are non-dimensional variables accepted:
![]() (27)
(27)
With equations of motion ![]()
![]()
![]()
Obtained average drift velocities were compared with theoretical ones [15] [16] .
Equations (28) are drift velocities for resonant charge exchange and elastic collision in weak fields when drift velocity is less than thermal velocity:
![]() (28)
(28)
at resonant charge exchange and elastic interaction correspondingly, where ![]() and
and![]() ―cross-sections for resonant charge exchange and elastic collision, respectively. Equations (29) are the corresponding values in strong fields:
―cross-sections for resonant charge exchange and elastic collision, respectively. Equations (29) are the corresponding values in strong fields:
![]() (29)
(29)
Equation (30) is the approximation used in intermediate fields:
![]() (30)
(30)
The results of simulation are given in Table 2 and Table 3![]() .
.
![]()
Table 2. Value of drift velocity ![]() at resonant charge exchange.
at resonant charge exchange.
![]()
Table 3. Value of drift velocity ![]() at elastic collisions.
at elastic collisions.
It is necessary to mention that computing time in “null-collision” method (in the same conditions) turned out to be 2 - 3 times less than in method of accumulation of probability. However, in case of large ![]() probability of collision increases more slowly than the velocity achieved for the time between collisions. That results in exceeding of drift velocity in the “null-collision” method. So at P = 0.2; 0.5; 0.8 this exceeding corresponded to approximately 4%; 16%; 40%, respectively.
probability of collision increases more slowly than the velocity achieved for the time between collisions. That results in exceeding of drift velocity in the “null-collision” method. So at P = 0.2; 0.5; 0.8 this exceeding corresponded to approximately 4%; 16%; 40%, respectively.
Method of accumulation of probability in strong and intermediate fields gives values close to theoretical ones. Accuracy is limited only by fluctuations of average velocity increasing when the total number of ions decreases and their temperature goes up. In weak fields calculated values of drift velocity in both methods exceed theoretical values to some extent (up to 5%). It can be caused by the fact that when Equations (28) are obtained inte-
grated square velocity is accepted as an average relative velocity:![]() .
.
4. Conclusion
The given effective models of calculating time between collisions by the method of accumulation of probability and ion angle velocities’ simulation after collision on the basis of solid spheres result in ion drift velocities close to theoretical ones and can be applied in the process of simulation of ion motion in heterogeneous plasma with non-constant concentration of atoms and ions and dependence of cross-section on velocity.
Acknowledgements
The work is done by the support of Program of strategic development of Petrozavodsk State University from 2012 to 2016, Ministry of Education of Russian Federation, contract No. 3.757.2014/K.