1. Introduction
The first known appearance of the Ince equation,
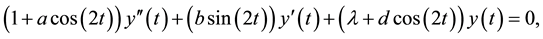
is in Whittaker’s paper ( [1] , Equation (5)) on integral equations. Whittaker emphasized the special case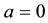 , and this special case was later investigated in more detail by Ince [2] [3] . Magnus and Winkler’s book [4] contains a chapter dealing with the coexistence problem for the Ince equation. Also Arscott [5] has a chapter on the Ince equation with
, and this special case was later investigated in more detail by Ince [2] [3] . Magnus and Winkler’s book [4] contains a chapter dealing with the coexistence problem for the Ince equation. Also Arscott [5] has a chapter on the Ince equation with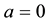 .
.
One of the important features of the Ince equation is that the corresponding Ince differential operator when applied to Fourier series can be represented by an infinite tridiagonal matrix. It is this part of the theory that makes the Ince equation particularly interesting. For instance, the coexistence problem which has no simple solution for the general Hill equation has a complete solution for the Ince equation (see [6] ).
When studying the Ince equation, it became apparent that many of its properties carry over to a more general class of equations “the generalized Ince equation”. These linear second order differential equations describe important physical phenomena which exhibit a pronounced oscillatory character; behavior of pendulum-like systems, vibrations, resonances and wave propagation are all phenomena of this type in classical mechanics, (see for example [7] ), while the same is true for the typical behavior of quantum particles (Schrödinger’s equa- tion with periodic potential [8] ).
2. The Differential Equation
We consider the Hill differential equation
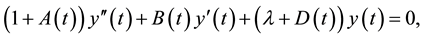 (2.1)
(2.1)
where
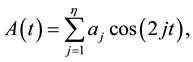
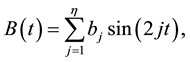
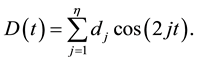
Here 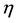 is a positive integer, the coefficients
is a positive integer, the coefficients 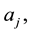

![]() for
for ![]() are specified real numbers.
are specified real numbers.
The real number ![]() is regarded as a spectral parameter. We further assume that
is regarded as a spectral parameter. We further assume that ![]() Unless stated otherwise solutions
Unless stated otherwise solutions ![]() are defined for
are defined for ![]() We will at times represent the coefficients
We will at times represent the coefficients ![]()
![]()
![]() for
for ![]() in the vector form:
in the vector form: ![]()
![]()
![]()
The polynomials
![]() (2.2)
(2.2)
will play an important role in the analysis of (2.1). For ease of notation we also introduce the polynomials
![]() (2.3)
(2.3)
Equation (2.1) is a natural generalization to the original Ince equation
![]() (2.4)
(2.4)
Ince’s equation by itself includes some important particular cases, if we choose for example ![]()
![]() we obtain the famous Mathieu’s equation
we obtain the famous Mathieu’s equation
![]() (2.5)
(2.5)
with associated pzlynomial
![]() (2.6)
(2.6)
If we choose ![]()
![]() and
and ![]() where
where ![]()
![]() are real numbers, Ince’s equation becomes Whittaker-Hill equation
are real numbers, Ince’s equation becomes Whittaker-Hill equation
![]() (2.7)
(2.7)
with associated polynomial
![]() (2.8)
(2.8)
Equation (2.1) can be brought to algebraic form by applying the transformation ![]() For example when
For example when ![]() and
and ![]() we obtain
we obtain
![]() (2.9)
(2.9)
3. Eigenvalues
Equation (2.1) is an even Hill equation with period![]() . We are interested in solutions which are even or odd and have period
. We are interested in solutions which are even or odd and have period ![]() or semi period
or semi period ![]() i.e.
i.e. ![]() We know that
We know that ![]() is a solution to (2.1) then
is a solution to (2.1) then ![]() and
and ![]() are also solutions. From the general theory of Hill equation (see [9] , Theorem 1.3.4); we obtain the following lemmas:
are also solutions. From the general theory of Hill equation (see [9] , Theorem 1.3.4); we obtain the following lemmas:
Lemma 3.1. Let ![]() be a solution of (2.1), then
be a solution of (2.1), then ![]() is even with period
is even with period ![]() if and only if
if and only if
![]() (3.1)
(3.1)
![]() is even with semi period
is even with semi period ![]() if and only if
if and only if
![]() (3.2)
(3.2)
![]() is odd with semi period
is odd with semi period ![]() if and only if
if and only if
![]() (3.3)
(3.3)
![]() is odd with period
is odd with period ![]() if and only if
if and only if
![]() (3.4)
(3.4)
Equation (2.1) can be written in the self adjoint form
![]() (3.5)
(3.5)
where
![]() (3.6)
(3.6)
Note that ![]() is even and
is even and ![]() -periodic since the function
-periodic since the function ![]() is continuous, odd, and
is continuous, odd, and ![]() - periodic.
- periodic.
Proof. Let ![]() (3.5) can be written as,
(3.5) can be written as,
![]() (3.7)
(3.7)
which is equivalent to
![]() (3.8)
(3.8)
Noting that
![]()
and
![]()
we see that
![]()
Therefore, (3.8) can be written as
![]() (3.9)
(3.9)
Since ![]() is strictly positive, the lemma follows. □
is strictly positive, the lemma follows. □
In the case of Ince’s Equation (2.4), we have the following formula for the function ![]()
![]() (3.10)
(3.10)
When ![]() the function can be computed explicitly using Maple. For example, let us consider the case
the function can be computed explicitly using Maple. For example, let us consider the case ![]() with
with ![]()
![]() Applying (3.6), we obtain
Applying (3.6), we obtain
![]()
Equation (2.1) with one of the boundary conditions in lemma 3.1 is a regular Sturm-Liouville problem. From the theory of Sturm-Liouville ordinary differential equations it is known that such an eigenvalue problem has a sequence of eigenvalues that converge to infinity. These eigen values are denoted by ![]()
![]()
![]() and
and ![]()
![]() to correspond to the boundary conditions in lemma 3.1 respectively. This notation is consistent with the theory of Mathieu and Ince’s equations (see [4] [10] ). Lemma 3.1 implies the following theorem.
to correspond to the boundary conditions in lemma 3.1 respectively. This notation is consistent with the theory of Mathieu and Ince’s equations (see [4] [10] ). Lemma 3.1 implies the following theorem.
Theorem 3.2. The generalized Ince equation admits a nontrivial even solution with period ![]() if and only if
if and only if ![]() for some
for some ![]() it admits a nontrivial even solution with semi-period
it admits a nontrivial even solution with semi-period ![]() if and only if
if and only if ![]() for some
for some ![]() it admits a nontrivial odd solution with semi-period
it admits a nontrivial odd solution with semi-period ![]() if and only if
if and only if ![]() for some
for some ![]() it admits a nontrivial odd solution with period
it admits a nontrivial odd solution with period ![]() if and only if
if and only if ![]() for some
for some ![]()
Example 3.3. To gain some understanding about the notation we consider the almost trivial completely solvable example, the so called Cauchy boundary value problem
![]() (3.11)
(3.11)
subject to the boundary conditions of lemma 3.1. We have the following for the eigenvalues ![]() in terms of
in terms of![]() .
.
1) Even with period ![]() we have
we have ![]()
2) Even with semi-period ![]() we have
we have ![]()
3) Odd with semi-period ![]() we have
we have ![]()
4) Odd with semi-period ![]() we have
we have![]() .
.
The formal adjoint of the generalized Ince equation is
![]() (3.12)
(3.12)
By introducing the functions
![]()
![]()
we note that the adjoint of (2.1) has the same form and can be written in the following form:
![]() (3.13)
(3.13)
Lemma 3.4. If ![]() is twice differentiable defined on
is twice differentiable defined on ![]() then,
then, ![]() is a solution to the generalized Ince equation if and only if
is a solution to the generalized Ince equation if and only if ![]() is a solution to its adjoint.
is a solution to its adjoint.
Proof. We Know that
![]()
and
![]()
For ease of notation, let
![]()
then
![]()
Substituting for ![]()
![]()
![]() and
and ![]() and simplifying we obtain
and simplifying we obtain
![]() □
□
From lemma 3.4 we know that if ![]() is twice differentiable,
is twice differentiable, ![]() is a solution to the generalized Ince’s equation with parameters
is a solution to the generalized Ince’s equation with parameters ![]()
![]()
![]() and
and ![]() if and only if
if and only if ![]() is a solution to its formal adjoint. Since the function
is a solution to its formal adjoint. Since the function ![]() is even with period
is even with period![]() , the boundary condition for
, the boundary condition for ![]() and
and ![]() are the same. Therefore we have the following theorem.
are the same. Therefore we have the following theorem.
Theorem 3.5. We have for ![]()
![]() (3.14)
(3.14)
![]() (3.15)
(3.15)
From Sturm-Liouville theory we obtain the following statement on the distribution of eigenvalues.
Theorem 3.6. The eigenvalues of the generalized Ince equation satisfy the inequalities
![]() (3.16)
(3.16)
The theory of Hill equation [4] gives the following results.
Theorem 3.7. If ![]() or
or ![]() belongs to one of the closed intervals with distinct endpoints
belongs to one of the closed intervals with distinct endpoints ![]()
![]()
![]() then the generalized Ince equation is unstable. For all other real values of
then the generalized Ince equation is unstable. For all other real values of ![]() the equation is stable. In the case
the equation is stable. In the case
![]() (3.17)
(3.17)
for some positive integer ![]() and the parameters
and the parameters ![]()
![]()
![]() the degenerate interval
the degenerate interval ![]() is not an instability interval: The generalized Ince equation is stable if
is not an instability interval: The generalized Ince equation is stable if
![]()
4. Eigenfunctions
By theorem 3.2, the generalized Ince’s equation with ![]() admits a non trivial even solution with period
admits a non trivial even solution with period![]() . It is uniquely determined up to a constant factor. We denote this Ince function by
. It is uniquely determined up to a constant factor. We denote this Ince function by ![]() when it is normalized by the conditions
when it is normalized by the conditions ![]() and
and
![]() (4.1)
(4.1)
The generalized Ince’s equation with ![]() admits a non trivial even solution with semi-period
admits a non trivial even solution with semi-period![]() . It is uniquely determined up to a constant factor. We denote this Ince function by
. It is uniquely determined up to a constant factor. We denote this Ince function by ![]() when it is normalized by the conditions
when it is normalized by the conditions ![]() and
and
![]() (4.2)
(4.2)
The generalized Ince equation with ![]() admits a non trivial odd solution with semi-period
admits a non trivial odd solution with semi-period![]() . It is uniquely determined up to a constant factor. We denote this Ince function by
. It is uniquely determined up to a constant factor. We denote this Ince function by ![]() when it is normalized by the conditions
when it is normalized by the conditions ![]() and
and
![]() (4.3)
(4.3)
The generalized Ince equation with ![]() admits a non trivial odd solution with period
admits a non trivial odd solution with period![]() . It is uniquely determined up to a constant factor. We denote this Ince function by
. It is uniquely determined up to a constant factor. We denote this Ince function by ![]() when it is normalized by the conditions
when it is normalized by the conditions ![]() and
and
![]() (4.4)
(4.4)
From Sturm-Liouville theory ( [11] Chapter 8, Theorem 2.1) we obtain the following oscillation properties.
Theorem 4.1. Each of the function systems
![]() (4.5)
(4.5)
![]() (4.6)
(4.6)
![]() (4.7)
(4.7)
![]() (4.8)
(4.8)
is orthogonal over ![]() with respect to the weight
with respect to the weight![]() , that is, for
, that is, for ![]()
![]() (4.9)
(4.9)
![]() (4.10)
(4.10)
![]() (4.11)
(4.11)
![]() (4.12)
(4.12)
Moreover, each of the previous system is complete over![]() .
.
Using the transformations that led to Theorem 3.5, we obtain the following result.
Theorem 4.2. We have
![]() , (4.13)
, (4.13)
![]() , (4.14)
, (4.14)
where ![]() and
and ![]() are positive and independent of
are positive and independent of ![]() and
and
![]()
with
![]()
The adopted normalization of Ince functions is easily expressible in terms of the Fourier coefficients of Ince functions and so is well suited for numerical computations [6] ; However, it has the disadvantage that Equations (4.13) and (4.14) require coefficients ![]() and
and ![]() which are not explicitly known.
which are not explicitly known.
Of course, once the generalized Ince functions ![]() and
and ![]() are known we can express
are known we can express ![]() and
and ![]() in the form
in the form
![]() (4.15)
(4.15)
![]() (4.16)
(4.16)
If we square both sides of (4.13) and (4.14) and integrate, we find that
![]() (4.17)
(4.17)
![]() (4.18)
(4.18)
If ![]() is very simple, then it is possible to evaluate the integrals in (4.17), (4.18) in terms of the Fourier coefficients of the generalized Ince functions. This provides another way to to calculate
is very simple, then it is possible to evaluate the integrals in (4.17), (4.18) in terms of the Fourier coefficients of the generalized Ince functions. This provides another way to to calculate ![]() and
and![]() .
.
Once we know ![]() and
and![]() , we can evaluate the integrals on the left-hand sides of the following equations
, we can evaluate the integrals on the left-hand sides of the following equations
![]() (4.19)
(4.19)
![]() (4.20)
(4.20)
The integrals on the right-hand sides of (4.19) and (4.20) are easy to calculate once we know the Fourier series of Ince functions.
5. Operators and Banded Matrices
In this section we introduce four linear operators associated with Equation (2.1), and represent them by banded matrices of width ![]() It is this simple representation that is fundamental in the theory of the generalized Ince equation. We assume known some basic notions from spectral theory of operators in Hilbert space.
It is this simple representation that is fundamental in the theory of the generalized Ince equation. We assume known some basic notions from spectral theory of operators in Hilbert space.
Let ![]() be the Hilbert space consisting of even, locally square-summable functions
be the Hilbert space consisting of even, locally square-summable functions ![]() with period
with period![]() . The inner product is given by
. The inner product is given by
![]() (5.1)
(5.1)
By restricting functions to ![]()
![]() is isometrically isomorphic to the standard
is isometrically isomorphic to the standard![]() . We also consider a second inner product
. We also consider a second inner product
![]() (5.2)
(5.2)
We consider the differential operator
![]() (5.3)
(5.3)
The domain ![]() of definition of consists of all functions
of definition of consists of all functions ![]() for which
for which ![]() and
and ![]() are absolutely continuous and
are absolutely continuous and![]() , by restricting functions to
, by restricting functions to![]() , this corresponds to the usual domain of a Sturm- Liouville operator associated with the boundary conditions (3.1). It is known ( [12] Chapter V, Section 3.6) that
, this corresponds to the usual domain of a Sturm- Liouville operator associated with the boundary conditions (3.1). It is known ( [12] Chapter V, Section 3.6) that ![]() is self-adjoint with compact resolvent when considered as an operator in
is self-adjoint with compact resolvent when considered as an operator in![]() , and its eigenvalues are
, and its eigenvalues are ![]()
![]() All eigenvalues of
All eigenvalues of ![]() are simple. If we consider
are simple. If we consider ![]() as an operator in the Hilbert space
as an operator in the Hilbert space ![]() then its adjoint
then its adjoint ![]() is given by the operator
is given by the operator
![]()
on the same domain ![]() see ( [12] , Chapter III, Example 5.32). The adjoint
see ( [12] , Chapter III, Example 5.32). The adjoint ![]() is of the same form as
is of the same form as ![]() but with
but with ![]()
![]() replaced by
replaced by ![]()
![]() respectively. By Theorem 3.5, we see that
respectively. By Theorem 3.5, we see that ![]() has the same eigen- values as
has the same eigen- values as ![]() Let
Let ![]() be the space of square-summable sequences
be the space of square-summable sequences ![]() with its standard inner product
with its standard inner product ![]() Then
Then
![]()
defines a bijective linear map ![]() Consider the operator
Consider the operator ![]() defined on
defined on
![]() (5.4)
(5.4)
Let ![]() denotes the sequence with a 1 in the
denotes the sequence with a 1 in the ![]() position and 0’s in all other positions, we also define
position and 0’s in all other positions, we also define ![]() i.e.
i.e. ![]() and
and ![]() for
for ![]() We find that the operator
We find that the operator ![]() can be represented in the following way,
can be represented in the following way,
![]() (5.5)
(5.5)
where ![]() and
and ![]() if
if ![]() and
and ![]()
![]() Note that the factor
Note that the factor ![]() should appear only with
should appear only with ![]()
![]() is self-adjoint with compact resolvent in
is self-adjoint with compact resolvent in ![]() equipped with the inner product
equipped with the inner product ![]() This inner product generates a norm that is equivalent to the usual
This inner product generates a norm that is equivalent to the usual ![]() The operator
The operator ![]() has the eigenvalues
has the eigenvalues ![]() and the corresponding eigenvectors form sequences of Fourier coefficients for the functions
and the corresponding eigenvectors form sequences of Fourier coefficients for the functions ![]()
Now consider the operator ![]() that is defined as
that is defined as ![]() in (5.3) but in the Hilbert space
in (5.3) but in the Hilbert space ![]() consisting of even functions with semi-period
consisting of even functions with semi-period![]() . This operator has eigenvalues
. This operator has eigenvalues ![]() with eigenfunctions
with eigenfunctions ![]()
![]() Using the basis
Using the basis ![]()
![]() then,
then,
![]()
defines a bijective linear map ![]() Consider the operator
Consider the operator ![]() defined on
defined on
![]()
Let ![]() for
for ![]() we get the following formula for
we get the following formula for ![]()
![]() (5.6)
(5.6)
where
![]()
Now consider the operator ![]() that is defined as
that is defined as ![]() but in the Hilbert space
but in the Hilbert space ![]() consisting of odd functions with semi-period
consisting of odd functions with semi-period![]() . This operator has the eigenvalues
. This operator has the eigenvalues ![]() with eigenfunctions
with eigenfunctions ![]()
![]() Using the basis functions
Using the basis functions ![]()
![]()
![]()
defines a bijective linear map ![]() Consider the operator
Consider the operator ![]() defined on
defined on
![]()
Let ![]() for
for ![]() we have the following formula for
we have the following formula for ![]()
![]() (5.7)
(5.7)
where
![]()
and
![]()
Finally, consider the operator ![]() that is defined as
that is defined as ![]() but in the Hilbert space
but in the Hilbert space ![]() consisting of odd functions with period
consisting of odd functions with period![]() . This operator has the eigenvalues
. This operator has the eigenvalues ![]() with eigenfunctions
with eigenfunctions ![]()
![]() Using the basis
Using the basis ![]()
![]()
![]()
defines a bijective linear map![]() . Consider the operator
. Consider the operator ![]() defined on
defined on
![]()
Let ![]() for
for ![]() Then, the formula for
Then, the formula for ![]() is
is
![]() (5.8)
(5.8)
where
![]()
Example 5.1. For the Whittaker-Hill Equation (2.7) in the following form [8]
![]() (5.9)
(5.9)
the function ![]() from (3.6) is equal to 1, therefore the operators
from (3.6) is equal to 1, therefore the operators ![]()
![]() are self-adjoint on the Hilbert spaces
are self-adjoint on the Hilbert spaces ![]()
![]() respectively. Hence the infinite matrices
respectively. Hence the infinite matrices ![]()
![]() are sy- mmetric. They are represented by
are sy- mmetric. They are represented by
![]() (5.10)
(5.10)
![]() (5.11)
(5.11)
![]() (5.12)
(5.12)
![]() (5.13)
(5.13)
6. Fourier Series
The generalized Ince functions admit the following Fourier series expansions
![]() (6.1)
(6.1)
![]() (6.2)
(6.2)
![]() (6.3)
(6.3)
![]() (6.4)
(6.4)
We did not indicate the dependence of the Fourier coefficients on ![]()
![]() The normalization of Ince functions implies
The normalization of Ince functions implies
![]() (6.5)
(6.5)
![]() (6.6)
(6.6)
![]() (6.7)
(6.7)
![]() (6.8)
(6.8)
Using relations (4.13) and (4.14), we can represent the generalized functions in a different way
![]() (6.9)
(6.9)
![]() (6.10)
(6.10)
where
![]()
Therefore, we can write
![]() (6.11)
(6.11)
![]() (6.12)
(6.12)
![]() (6.13)
(6.13)
![]() (6.14)
(6.14)
where
![]()
and the Fourier coefficients ![]() and
and ![]() belong to the parameters
belong to the parameters ![]() Properties of the coefficients
Properties of the coefficients ![]() and
and ![]() follow from those of
follow from those of ![]() and
and ![]()
A generalized Ince function is called a generalized Ince polynomial of the first kind if its Fourier series (6.1), (6.2), (6.3), or (6.4) terminate. It is called a generalized Ince polynomial of the second kind if its expansion (6.11), (6.12), (6.13), or (6.14) terminate. If they exist, these generalized Ince polynomials and their corresponding eigenvalues can be computed from the finite subsections of the matrices ![]()
![]() of Section 5.
of Section 5.
Example 6.1. Consider the equation
![]() (6.15)
(6.15)
one can check that if we set ![]() any constant function
any constant function ![]() is an eigenfunction corresponding to the eigenvalue
is an eigenfunction corresponding to the eigenvalue ![]() The adopted normalization of Section 4 implies that
The adopted normalization of Section 4 implies that ![]() It is a generalized Ince polynomial (even with period
It is a generalized Ince polynomial (even with period![]() ).
).