Compactness of Composition Operators from the p-Bloch Space to the q-Bloch Space on the Classical Bounded Symmetric Domains ()
1. Introduction
Let  be a bounded homogeneous domain in
be a bounded homogeneous domain in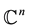 . The class of all holomorphic functions on
. The class of all holomorphic functions on 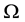 will be denoted by
will be denoted by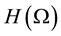 . For
. For 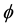 a holomorphic self-map of
a holomorphic self-map of  and
and , the composition
, the composition  is denoted by
is denoted by![]() , and
, and ![]() is called the composition operator with symbol
is called the composition operator with symbol![]() .
.
The composition operators as well as related operators known as the weighted composition operators between the weighted Bloch spaces were investigated in [1] [2] in the case of the unit disk, and in [3] - [7] for the case of the unit ball. The study of the weighted composition operators from the Bloch space to the Hardy space ![]() was carried out in [8] [9] for the unit ball. Characterizations of the boundedness and the compactness of the composition operators and the weighted ones between the Bloch spaces were given in [10] - [12] for the polydisc case, and in [13] - [18] for the case of the bounded symmetric domains. Furthermore, we will give some results about the composition operators for the case of the weighted Bloch space on the bounded symmetric domains.
was carried out in [8] [9] for the unit ball. Characterizations of the boundedness and the compactness of the composition operators and the weighted ones between the Bloch spaces were given in [10] - [12] for the polydisc case, and in [13] - [18] for the case of the bounded symmetric domains. Furthermore, we will give some results about the composition operators for the case of the weighted Bloch space on the bounded symmetric domains.
In 1930s all irreducible bounded symmetric domains were divided into six types by E. Cartan. The first four types of irreducible domains are called the classical bounded symmetric domains, the other two types, called exceptional domains, consist of one domain each (a 16 and 27 dimensional domain).
The first three types of classical bounded symmetric domains can be expressed as follows [19] :
![]() ,
,
where ![]() and
and ![]() is the
is the ![]() identity matrix,
identity matrix, ![]() is the transpose of
is the transpose of![]() ;
;
![]()
![]()
Let ![]() and
and![]() . The Kronecker product
. The Kronecker product ![]() of
of ![]() and
and ![]() is defined as the
is defined as the ![]()
matrix ![]() such that the element at the
such that the element at the ![]() -th row and
-th row and ![]() -th column
-th column ![]() [19] . Then the Berg- man metric of
[19] . Then the Berg- man metric of ![]() is as follows (see [19] ):
is as follows (see [19] ):
![]() (1.1)
(1.1)
where ![]() is a complex vector,
is a complex vector, ![]() is the conjugate transpose of
is the conjugate transpose of![]() , and
, and
![]() .
.
Following Timoney’s approach (see [18] ), a holomorphic function ![]() is in the Bloch space
is in the Bloch space![]() , if
, if
![]()
Now we define a holomorphic function ![]() to be in the p-Bloch space
to be in the p-Bloch space![]() , if
, if
![]() (1.2)
(1.2)
where
![]()
![]()
We can prove that ![]() is a Banach space with norm
is a Banach space with norm ![]() which is similar
which is similar
with the case on ![]()
Let ![]() be a holomorphic self-map of
be a holomorphic self-map of![]() . We are concerned here with the question of when
. We are concerned here with the question of when
![]() will be a compact operator.
will be a compact operator.
Let ![]() denote a diagonal matrix with diagonal elements
denote a diagonal matrix with diagonal elements![]() . In this work,we shall de- note by
. In this work,we shall de- note by ![]() a positive constant, not necessarily the same on each occurrence.
a positive constant, not necessarily the same on each occurrence.
In Section 2, we prove the equivalence of the norms defined in this paper and in [20] .
In Section 3, we state several auxiliary results most of which will be used in the proofs of the main results.
Finally, in Section 4, we establish the main result of the paper. We give a sufficient and necessary condition for the composition operator Cf from the p-Bloch space ![]() to the q-Bloch space
to the q-Bloch space ![]() to be compact, where
to be compact, where ![]() and
and![]() . Specifically,we prove the following result:
. Specifically,we prove the following result:
Theorem 1.1. Let ![]() be a holomorphic self-map of
be a holomorphic self-map of![]() . Then
. Then ![]() is compact if and only if, for every
is compact if and only if, for every![]() , there exists a
, there exists a ![]() such that
such that
![]() (1.3)
(1.3)
for all ![]() whenever
whenever![]() ,
,![]() .
.
The compactness of the composition operators for the weighted Bloch space on the bounded symmetric domains of ![]() is similar with the case of
is similar with the case of![]() ; we omit the details.
; we omit the details.
2. The Equivalence of the Norms
Denote [20] ![]() .
.
Lemma 2.1. (Bloomfield-Watson) [21] Let ![]() be an
be an ![]() Hermitian matrix. Then
Hermitian matrix. Then
![]() (2.1)
(2.1)
where ![]() is any
is any ![]() matrix and satisfies
matrix and satisfies![]() .
.
Theorem 2.1. ![]() and
and ![]() are equivalent.
are equivalent.
Proof. The metric matrix of ![]() is
is
![]()
For any![]() , let
, let ![]() with
with![]() . Then
. Then
![]()
Denote ![]() then
then![]() ,
, ![]() and
and
![]()
Thus
![]()
Hence
![]()
Furthermore,
![]()
Since
![]()
Thus
![]() (2.2)
(2.2)
For
![]()
then we have
![]() (2.3)
(2.3)
Combining (2.2) and (2.3),
![]()
Next,
![]()
and
![]()
Therefore, the proof is completed. □
3. Some Lemmas
Here we state several auxiliary results most of which will be used in the proof of the main result.
Lemma 3.1. [18] Let ![]() be a bounded homogeneous domain. Then there exists a constant
be a bounded homogeneous domain. Then there exists a constant![]() , depending only on
, depending only on![]() , such that
, such that
![]() (3.1)
(3.1)
for each ![]() whenever f holomorphically maps
whenever f holomorphically maps ![]() into itself. Here
into itself. Here ![]() denotes the Bergman metric
denotes the Bergman metric
on![]() ,
, ![]() denotes the Jacobian matrix of
denotes the Jacobian matrix of![]() .
.
Lemma 3.2. Let ![]() be a holomorphic self-map of
be a holomorphic self-map of ![]() and
and ![]() a compact subset of
a compact subset of![]() .Then there exists a constant
.Then there exists a constant ![]() such that
such that
![]() (3.2)
(3.2)
for all ![]() whenever
whenever![]() .
.
Proof. For![]() , let
, let ![]()
For any compact![]() , there exists a constant
, there exists a constant ![]() such that
such that![]() . Then there exists
. Then there exists
![]() such that
such that![]() , whenever
, whenever![]() .
.
Thus
![]() (3.3)
(3.3)
Combining Lemma 3.1 with (3.3) shows that (3.2) holds. □
Lemma 3.3. (Hadamard) [21] Let ![]() be an
be an ![]() Hermitian matrix. Then
Hermitian matrix. Then
![]() (3.4)
(3.4)
and equality holds if and only if ![]() is a diagonal matrix.
is a diagonal matrix.
Lemma 3.4. Let![]() . Then
. Then
![]() (3.5)
(3.5)
Proof. For any![]() , we have
, we have ![]()
Thus we have![]() ,
, ![]()
It follows from Lemma 3.3 that ![]() □
□
Lemma 3.5. Let ![]() be a classical bounded symmetric domain, and
be a classical bounded symmetric domain, and ![]() denote its metric matrix. Then a holomorphic function
denote its metric matrix. Then a holomorphic function ![]() on
on ![]() is in
is in ![]() if and only if
if and only if
![]() (3.6)
(3.6)
If (3.6) holds, then
![]() (3.7)
(3.7)
Proof. We can get the conclusion by the process of the proof on Theorem 2.1. □
Lemma 3.6. [18] Let
![]()
![]()
![]()
where ![]() and
and ![]() are unitary matrices and
are unitary matrices and ![]()
Denote![]() ,
,![]() . Then
. Then
(1) ![]()
(2) ![]()
(3)![]() ;
;
(4) ![]() for
for![]() ;
;
(5) ![]() for
for![]() ;
;
(6) ![]() for
for![]() .
.
Lemma 3.7. ![]() is compact if and only if
is compact if and only if ![]() as
as ![]() for
for
any bounded sequence ![]() in
in ![]() that converges to 0 uniformly on compact subsets of
that converges to 0 uniformly on compact subsets of![]() .
.
Proof. The proof is trial by using the normal methods. □
4. Proof of Theorem 1.1
Proof. Let ![]() be a bounded sequence in
be a bounded sequence in ![]() with
with![]() , and
, and ![]() uniformly on compact subsets of
uniformly on compact subsets of![]() .
.
Suppose (1.3) holds. Then for any![]() , there exists a
, there exists a![]() , such that
, such that
![]() (4.1)
(4.1)
for all ![]() whenever
whenever ![]() and
and![]() .
.
By the chain rule, we have![]() .
.
If ![]() and
and![]() , then we get
, then we get![]() . If
. If ![]() and
and![]() , then
, then
![]() (4.2)
(4.2)
It follows from (4.1) and (4.2) that
![]()
![]() (4.3)
(4.3)
![]() (4.4)
(4.4)
whenever ![]() and
and![]() .
.
On the other hand, there exists a constant ![]() such that
such that
![]()
So if![]() , then
, then
![]()
We assume that ![]() converges to 0 uniformly on compact subsets of
converges to 0 uniformly on compact subsets of![]() . By Weierstrass Theorem, it is easy to see that
. By Weierstrass Theorem, it is easy to see that ![]() converges to 0 uniformly on compact subsets of
converges to 0 uniformly on compact subsets of![]() . Thus, for given
. Thus, for given![]() , there exists
, there exists ![]() large enough such that
large enough such that
![]() (4.5)
(4.5)
for any![]() ,
, ![]() whenever
whenever ![]() and
and![]() . Then by in- equalities (4.3) and (4.5) and Lemma 3.2, it follows that, for
. Then by in- equalities (4.3) and (4.5) and Lemma 3.2, it follows that, for ![]() large enough,
large enough,
![]() (4.6)
(4.6)
whenever ![]() and
and![]() .
.
Combining (4.4) and (4.6) shows that ![]() as
as ![]() large enough. So
large enough. So
![]() is compact.
is compact.
For the converse, arguing by contradiction, suppose ![]() is compact and
is compact and
the condition (1.3) fails. Then there exist an![]() , a sequence
, a sequence ![]() in
in ![]() with
with
![]() as
as ![]() and a sequence
and a sequence ![]() in
in![]() , such that
, such that
![]() (4.7)
(4.7)
for all![]() .
.
Now we will construct a sequence of functions ![]() satisfying the following three conditions :
satisfying the following three conditions :
(I) ![]() is a bounded sequence in
is a bounded sequence in![]() ;
;
(II) ![]() tends to 0 uniformly on any compact subset of
tends to 0 uniformly on any compact subset of![]() ;
;
(III) ![]()
The existence of this sequence will contradict the compactness of![]() .
.
We will construct the sequence of functions ![]() according to the following four parts: A - D.
according to the following four parts: A - D.
Part A: Suppose that ![]()
where ![]() is the
is the ![]() matrix whose element at the
matrix whose element at the ![]() row and
row and ![]() column is 1 and the other elements are 0. Since
column is 1 and the other elements are 0. Since ![]() maps
maps ![]() into itself,
into itself, ![]() and
and ![]()
Denote ![]() by
by ![]() Using formula (1.1), we have
Using formula (1.1), we have
![]()
Denote
![]()
then
![]() (4.8)
(4.8)
We construct the sequence of functions ![]() according to the following three different cases.
according to the following three different cases.
Case 1. If for some![]() ,
,
![]() (4.9)
(4.9)
then set
![]() (4.10)
(4.10)
where ![]() is any positive number.
is any positive number.
Case 2. If for some![]() ,
,
![]() (4.11)
(4.11)
then set
![]() (4.12)
(4.12)
where![]() , if for some
, if for some![]() ,
, ![]() or for some
or for some![]() ,
, ![]() , replace the corresponding term
, replace the corresponding term ![]() by 0 (the same below).
by 0 (the same below).
Case 3. If for some![]() ,
,
![]() (4.13)
(4.13)
then set
![]() (4.14)
(4.14)
Next, we will prove that the sequences of functions ![]() defined by (4.10), (4.12) and (4.14) all satisfy the conditions (I), (II) and (III).
defined by (4.10), (4.12) and (4.14) all satisfy the conditions (I), (II) and (III).
To begin with, we will prove the sequence of functions ![]() defined by (4.10) satisfies the three con- ditions. We can get that
defined by (4.10) satisfies the three con- ditions. We can get that
![]()
It follows from Lemma 3.5 that![]() .
.
This proves that the sequence of functions ![]() defined by (4.10) satisfies condition (I).
defined by (4.10) satisfies condition (I).
Let ![]() be any compact subset of
be any compact subset of![]() . Then there exists a
. Then there exists a ![]() such that
such that
![]() (4.15)
(4.15)
for any![]() . By (4.10), we have
. By (4.10), we have
![]()
Since
![]()
But ![]() as
as![]() . Thus,
. Thus, ![]() converges to 0 uniformly on
converges to 0 uniformly on![]() . Therefore,
. Therefore,
![]() converges to 0 uniformly on
converges to 0 uniformly on ![]() as
as![]() . Thus, the sequence of functions
. Thus, the sequence of functions ![]() defined by (4.10) satisfies the condition (II).
defined by (4.10) satisfies the condition (II).
Now (4.8) and (4.9) mean that
![]() (4.16)
(4.16)
Combining (4.7) and (4.16), we have
![]()
Since
![]()
This proves that ![]() as
as![]() , which means that the sequence of functions
, which means that the sequence of functions ![]() defined by (4.10) satisfies condition (III).
defined by (4.10) satisfies condition (III).
We can prove that the sequence of functions ![]() defined by (4.12) or (4.14) satisfies the conditions (I) - (III) by using the analogous method as above.
defined by (4.12) or (4.14) satisfies the conditions (I) - (III) by using the analogous method as above.
Part B: Now we assume that
![]()
It is clear that ![]() and for
and for ![]() we can assume that
we can assume that ![]() and
and ![]() as
as![]() , where
, where![]() .
.
If![]() , we can use the same methods as in Part A to construct a sequence of functions
, we can use the same methods as in Part A to construct a sequence of functions ![]() satisfy- ing conditions (I)-(III).
satisfy- ing conditions (I)-(III).
Using formula (1.1), we have
![]()
Denote
![]()
Then,
![]() (4.17)
(4.17)
We construct the sequence of functions ![]() according to the following six different cases.
according to the following six different cases.
Case 1. If for some![]() ,
,
![]()
then set
![]() (4.18)
(4.18)
Case 2. If for some![]() ,
,
![]()
then set
![]() (4.19)
(4.19)
Case 3. If for some![]() ,
,
![]()
then set
![]() (4.20)
(4.20)
Case 4. If for some![]() ,
,
![]()
then set
![]() (4.21)
(4.21)
Case 5. If for some![]() ,
,
![]()
then set
![]() (4.22)
(4.22)
Case 6. If for some![]() ,
,
![]()
then set
![]() (4.23)
(4.23)
By using the same methods as in Part A, we can prove the sequences of functions ![]() defined by (4.18)-(4.23) satisfying conditions (I) - (III).
defined by (4.18)-(4.23) satisfying conditions (I) - (III).
Now, as an example,we will prove that the sequence of functions ![]() defined by (4.19) satisfying the conditions (I) - (III).
defined by (4.19) satisfying the conditions (I) - (III).
For any![]() , we have
, we have
![]() (4.24)
(4.24)
Thus
![]()
By Lemma![]() , we have
, we have
![]() (4.25)
(4.25)
It follows from Lemma 3.5 and (4.25) that![]() . This proves that the sequence of functions
. This proves that the sequence of functions ![]() defined by (4.19) satisfy the condition (I).
defined by (4.19) satisfy the condition (I).
Let ![]() be any compact subset of
be any compact subset of![]() . Since there exists a
. Since there exists a ![]() such that
such that![]() ,
, ![]() Thus
Thus
![]()
Since
![]()
So ![]() as
as![]() . Thus,
. Thus, ![]() converges to 0 uni-
converges to 0 uni-
formly on E. Therefore,the sequence of ![]() converges to 0 uniformly on
converges to 0 uniformly on ![]() as
as![]() . Thus, the sequence of functions
. Thus, the sequence of functions ![]() defined by (4.19) satisfies the condition (II).
defined by (4.19) satisfies the condition (II).
For case 2,
![]() (4.26)
(4.26)
Combining (4.7) and (4.26), we have
![]()
Since
![]()
This proves that ![]() as
as![]() , which means that the sequence of functions
, which means that the sequence of functions ![]() defined by (4.19) satisfies condition (III).
defined by (4.19) satisfies condition (III).
If![]() , then by Lemma 3.6, there exist
, then by Lemma 3.6, there exist ![]() and
and ![]() in
in ![]() such that
such that
![]()
If we denote![]() , then
, then ![]() and
and
![]() , where.
, where.
Denote![]() , where the sequence of functions
, where the sequence of functions ![]() is the sequence obtained in Part A. We have
is the sequence obtained in Part A. We have
![]() (4.27)
(4.27)
where ![]() and
and![]() . Now (4.27) implies that
. Now (4.27) implies that
![]()
and
![]()
It is clear that![]() , and combining the discussion in Part A,we can get that
, and combining the discussion in Part A,we can get that
![]() as
as![]() ; that means the sequence of functions
; that means the sequence of functions ![]() satisfies condition (III).
satisfies condition (III).
We prove that the sequence of functions ![]() is a bounded sequence in
is a bounded sequence in![]() .
.
Since![]() ,
,
![]()
So ![]() is bounded.
is bounded.
Next we prove that ![]() converges to 0 uniformly on any compact subset
converges to 0 uniformly on any compact subset ![]() of
of![]() . Let
. Let
![]() then by the definition of
then by the definition of ![]() and Lemma 3.6, we can get a calculation directly that
and Lemma 3.6, we can get a calculation directly that
![]()
It is clear that ![]() converges uniformly to
converges uniformly to ![]() in
in![]() .
.
Since ![]() and
and![]() , there similarly exist
, there similarly exist ![]() in
in ![]() such that
such that
![]() , and the first component of
, and the first component of ![]() is
is![]() . It is clear that
. It is clear that ![]() is holo-
is holo-
morphic on![]() . Let
. Let ![]() for
for![]() . For
. For![]() , we know
, we know
![]() . We may choose
. We may choose ![]() such that
such that![]() . Thus, for
. Thus, for ![]() large enough,
large enough,
![]() and from this it follows that
and from this it follows that
![]()
by the definition of![]() ,
, ![]() converges to 0 uniformly on
converges to 0 uniformly on![]() .
.
Hence ![]() satisfies conditions (I)--(III), and this contradicts the compactness of
satisfies conditions (I)--(III), and this contradicts the compactness of![]() .
.
Part C: Assume that
![]()
where![]() . For
. For ![]() we may assume that
we may assume that![]() ,
, ![]() ,
, ![]()
![]() as
as![]() , where
, where![]() ,
,![]() .
.
Just as in Part B, we can use the same methods to prove the conclusion. And for![]() ,
, ![]() , we may only show the sequence of functions
, we may only show the sequence of functions ![]() which satisfy the conditions (I) - (III) here.
which satisfy the conditions (I) - (III) here.
Using formula (1.1), we have
![]()
Denote
![]()
then,
![]() (4.28)
(4.28)
We construct the sequence of functions ![]() according to the following three different cases.
according to the following three different cases.
Case 1. If for some![]() ,
,
![]()
then set
![]() (4.29)
(4.29)
Case 2. If for some![]() ,
,
![]()
then set
![]() (4.30)
(4.30)
Case 3. If for some![]() ,
,
![]()
then set
![]() (4.31)
(4.31)
Using the same methods as in Part A and Part B, we can prove the sequences of functions ![]() defined by (4.29)-(4.31) satisfying conditions (I) - (III).
defined by (4.29)-(4.31) satisfying conditions (I) - (III).
Part D: In the general situation. For![]() , there exist an
, there exist an ![]() unitary matrix
unitary matrix ![]() and an
and an ![]() unitary matrix
unitary matrix ![]() such that
such that
![]()
We may assume that ![]() and
and ![]() as
as![]() . Let
. Let ![]() and
and![]() ;
; ![]() means
means
that ![]() as
as ![]() for any
for any![]() ,
,![]() . Let
. Let ![]() and
and ![]() for
for
![]() . Of course, P is an
. Of course, P is an ![]() unitary matrix,
unitary matrix, ![]() is an
is an ![]() unitary matrix, and
unitary matrix, and ![]() con-
con-
verges uniformly to ![]() on
on![]() .
.
Let![]() ,
, ![]() where the sequence of
where the sequence of ![]() are the functions obtained in Part C.
are the functions obtained in Part C.
From the same discussion as that in Part B, we know that ![]() satisfies conditions (I) and (III). For the compact subset
satisfies conditions (I) and (III). For the compact subset![]() ,
, ![]() is also a compact subset of
is also a compact subset of![]() , so we can choose an open sub-
, so we can choose an open sub-
set ![]() of
of ![]() such that
such that![]() . Since
. Since ![]() converges uniformly to
converges uniformly to
![]() on
on![]() , it follows that
, it follows that ![]() as
as![]() . Since
. Since ![]() tends to 0 uniformly on
tends to 0 uniformly on![]() , we know
, we know ![]() tends to 0 uniformly on
tends to 0 uniformly on![]() . Thus,
. Thus, ![]() satisfies condition (II). □
satisfies condition (II). □
Acknowledgements
We thank the Editor and the referee for their comments. Research is funded by the National Natural Science Foundation of China (Grant No. 11171285) and the Postgraduate Innovation Project of Jiangsu Province of China (CXLX12-0980).
NOTES
*Corresponding author.