Obtaining a New Representation for the Golden Ratio by Solving a Biquadratic Equation

Leonardo Mondaini^1,2*

¹Department of Oncology, University of Alberta, Edmonton, Canada.
²Grupo de Física Teórica e Experimental, Departamento de Ciências Naturais, Universidade Federal do Estado do Rio de Janeiro, Rio de Janeiro, Brazil.

DOI: 10.4236/jamp.2014.213134                

Abstract

In the present work we show how different ways to solve biquadratic equations can lead us to different representations of its solutions. A particular equation which has the golden ratio and its reciprocal as solutions is shown as an example.

Keywords

Golden Ratio, Algebraic Equations, Recreational Mathematics, History of Mathematics

1. Introduction

The study of algebraic equations has occupied the brightest mathematical minds throughout many centuries. We must highlight among the main results of the studies in this area, the attainment of the formula for resolution of the general quadratic equations which, along with the formula for resolution of the general cubic equations achieved by Niccolo Fontana (Tartaglia)¹, led to the creation of complex numbers, since the application of these formulas led to a “misterious” thing: the square root of a negative number. The solution of general quartic equations by Ludovico Ferrari (a pupil of Cardano) comes to complete this picture, once it was established that a solution by radicals for generic equations of degree equal to or greater than 5 cannot be achieved (a result proved for the first time by the prodigies Niels Abel and Evariste Galois). In the present work, which may be classified into the field of recreational mathematics and is devoted to stimulate the interest of readers with pre- university level mathematical background as a way of inspiring their further study on the subject, we will focus on an interesting aspect associated to a particular kind of quartic equation, namely, the biquadratic one.

The rest of this work is organized as follows. A particular equation which has the golden ratio and its reciprocal as solutions is presented in Section 2. In Sections 3 and 4, we solve this equation by using two different algorithms. Finally, in Section 5, we present our concluding remarks.

2. An Interesting Equation

We start by considering the following characteristic equation [2] [3]

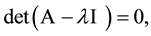(1)

where 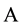is a symmetric real matrix defined by

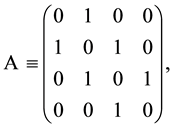(2)

and is the corresponding 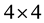identity matrix. Notice that we can rewrite Equation (1) in the following way

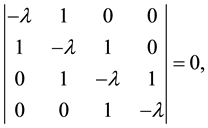(3)

or

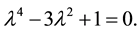(4)

This simple biquadratic equation displays an interesting feature. The form its solutions are expressed depends, apparently, on the algorithm used for solving it. Even more interesting is the fact that one of these algorithms yields the numbers and 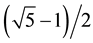(as well as their respective symmetrical ones) as solutions, which are the most known representation of this ubiquitous mathematical phenomenon, namely, the golden ratio [4] , and its reciprocal. This famous number appears historically as the solution of the quadratic equation

(5)

which is related to the geometrical problem of dividing a given line segment into what is called the golden section, which the celebrated astronomer Johannes Kepler called “one of the two Jewels of Geometry” (the second one being the Pythagorean theorem). Translated into mathematical language, the golden section means that the segment 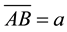is cut at a point 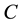so that the whole segment is in the same ratio to the larger part as 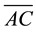is to the other part,. That is

(6)

This, in turn, leads to the quadratic equation already mentioned, the positive root of which is. Notice that when, the value is the reciprocal of the golden ratio, i.e., 0.6180339887... In the next sections we will apply two different algorithms in order to solve the Equation (4).

3. First Algorithm

Firstly, we will solve Equation (4) by using an algorithm very similar to the one originally employed by Ludovico Ferrari in his solution for the quartic equations (polynomial equations of the fourth degree)² [5] . In order to do that, we start by observing that Equation (4) can be also rewritten in the following way:

(7)

or

(8)

The left side of this equation, a perfect square, may be trivially simplified as

(9)

which implies that

(10)

or

(11)

When solving the above equations by using the well-known quadratic formula, we find that the solutions for the equation with are given by

(12)

whereas for the equation with (which is identical to Equation (5) with) we have the following solutions

(13)

Thus, the complete set of solutions of the original biquadratic equation is given by

(14)

where we remind again the reader that is the usual representation for the golden ratio, and is its reciprocal.

4. Second Algorithm

The second algorithm follows the conventional method to solve biquadratic equations. In such method we start by considering the following change of variables

, (15)

which allows us to reduce the Equation (4) to the form

(16)

A direct application of the quadratic formula yields the solutions

(17)

Since, we then have the following set of solutions for the original equation³

(18)

5. Concluding Remarks

We saw that apparently distinct solutions are obtained by solving Equation (4) by two different algorithms.

However, we can easily verify that they are identical. Just compute the square of and check it! We have then obtained a new representation for the golden ratio, namely

(19)

Acknowledgements

This work has been supported in part by CNPq.

NOTES

¹Usually the formula for resolution of the general cubic equation is attributed to Girolamo Cardano, and being thus it receives his name. A more detailed description about the dispute for the priority of this solution can be found in [1] .

²The goal of Ferrari’s algorithm for solving the general quartic is to have perfect squares in both sides of the equation.

³The solutions are displayed so as to indicate a direct correspondence with the set of solutions obtained with the first algorithm.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Boyer, C.B. and Merzbach, U.C. (1991) A History of Mathematics. 2nd Edition, John Wiley & Sons, Inc., New York.
[2]	Weisstein, E.W. Characteristic Equation. MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/CharacteristicEquation.html
[3]	Lipschutz, S. and Lipson, M. (2013) Linear Algebra—Schaum’s Outlines. 5th Edition, The McGraw-Hill Companies, Inc., New York.
[4]	Livio, M. (2002) The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number. Broadway Books, New York.
[5]	Cardano, G. (1993) Ars Magna or the Rules of Algebra. Dover Publications, Mineola.