1. Introduction
Tackling the Hillber’s 6th problem (mathematical treatment of the axioms of physics), axiomatization of quantum mechanics has been a success. The problem known as stair goes on the development of physics and mathematics. In the long view of history, Galileo was one of the first modern thinkers to clearly state that the laws of nature were mathematical. In his book The Assayer he wrote “Philosophy is written in this grand book, the universe... It is written in the language of mathematics, and its characters are triangles, circles, and other geometric figures; ...” [1] . Generally, the modern era in cosmology began with Albert Einstein’s 1915 formulation of general relativity [2] , which made it possible to quantitatively predict the origin, evolution, and conclusion of the universe as a whole; his sweeping extension of Newton’s theory of gravity, and the differential geometry is the mathematical basis of general relativity. By embedding gravity in a geometrical picture of space and time, Einstein was able to think in grand terms about the global structure of the universe [3] [4] . The positive energy theorem in general relativity demonstrated―sixty years after its discovery―that Einstein’s theory was consistent and stable [5] [6] . Most modern, accepted theories of cosmology are based on general relativity and, more specifically, the predicted Big Bang [7] [8] . In the universe, the axiom field represents a particularly attractive candidate for the dark matter [9] . Dark matter’s existence is inferred from gravitational effects on visible matter and gravitational lensing of background radiation [10] . Likewise, a significant amount of non-baryonic, cold matter is necessary to explain the large-scale structure of the universe [11] [12] . Hawking was able to come to his proof using mathematical techniques that had been developed by Roger Penrose [13] [14] . To solve the problem of the singularity, Hawking, Hertog and Reall introduced a virtual time and constructed the no-boundary universe model [15] . The Lambda Cold Dark Matter (abbreviated ΛCDM) model affords no explanation for dark energy and dark matter in physical cosmology. It is merely a useful parametric form of the Big Bang cosmological model [16] . In a manner of speaking, the matter and the antimatter have a close relationship and a mutual influence; matter plays a central role in cosmology, and black holes are a favorite testing ground for quantum gravity [17] . However, in this case, quantum-logic is a set of rules for reasoning about propositions which takes the principles of quantum theory into account [18] [19] . It seems that what is “logical system of cosmology” in physics is unknown. The problem will get surprisingly little attention from the cosmology world, yet this paper is an interesting step forward in exploring cosmological logic to some extent. So, we need an accurate law, no need for a hasty approximation. Let us start out by understanding set theory of the universe that axiom holds [20] . First of all, it is interesting to note that the set theory, cosmology and quantum mechanics have showed blood relationship, but then we also discover that the global geometry has a deep kinship with them. The aim of the research is to provide a powerful tool, and it is tempting to use the tool to solve big problems of cosmology, such as overcoming physical singularity of space-time using set operations. In cosmology, to introduce the principle of duality and the laws of mathematics is translated into the physical laws, i.e. use quantifiers to express the quantum mechanics object and cosmology object as a logical expression. The study found some of the physics laws such as the zero-point symbiosis law. We introduce the large-scale structure model of the universe. For explanation, we discuss some basic theories on the closed universe, open universe and lattice angle. How can we make mathematics model for antimatter? For example, when matter and antimatter meet, do they annihilate in a big explosion and convert their mass to energy? Still, to conclude this section, I am pushing to bring forward the axiom cosmology.
2. Cosmological Set Theory and Large-Scale Structure Models
The concept of set to appear in cosmology, only when the cosmology and set theory, which neatly unifies. In the background of the conception are the matter set and the antimatter set, and how to work with the operation and the rules. The universe axiom systems contain these set laws, that is, domination laws, identity laws, complementation laws, difference-set law and Liu’s law, etc. (see [20] ).
In addition, the cosmic set is a kind of application logic. This logic is said to be mathematical logic of the universe. The domination logic has a natural cosmology interpretation, and the explanation does not depend on experience, so we can use it to structure the cosmological mathematical structure. These logical inconsistencies can be avoided by building set theory starting with basic assumptions, called axioms; for instance, the identities of universe algebraic is used to model the astrophysics.
In this section, we will briefly describe some components of the cosmological sets, and go on to describe later in the article. Let us to view universe mathematically first and establish a geometry for it later. Sets can be represented graphically using curve. We draw a curved surface to indicate the universal set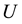 , which is the set of the curve. We use notation
, which is the set of the curve. We use notation 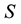 to denote the curve diagram of the sets,
to denote the curve diagram of the sets, 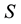 is a finite set. In curved surface, let
is a finite set. In curved surface, let  and
and 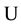 be a coordinate set of operation. Let
be a coordinate set of operation. Let 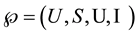 be a universe operation. The tow operations in cosmology that we will use most are
be a universe operation. The tow operations in cosmology that we will use most are  and
and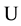 .
.
From general topology, a set 1 (one), called the space, whose elements are called points. So the following theorem will help us to compute a convex for the universe, and it will also be useful when we apply global geometry theory to depicting dark matter, dark energy and black holes.
2.1. Theorem (Curl of U)
In space, let 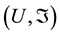 be a topological space, so
be a topological space, so
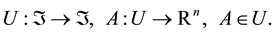 (1)
(1)
Let . The sector between the curve
. The sector between the curve 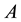 and the curve
and the curve 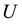 be a convex in Figure 1(a).
be a convex in Figure 1(a).
Explicit proof for the theorem: Let 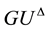 and
and 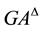 be drawing out two geodesics from vertex
be drawing out two geodesics from vertex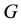 , and minimal neighborhood of the vertex G is split into two sectors
, and minimal neighborhood of the vertex G is split into two sectors ![]() and
and![]() . Let
. Let ![]() and
and ![]() be two points in sector P, and X, Y adjacent to
be two points in sector P, and X, Y adjacent to ![]() so that geodesic
so that geodesic ![]() cannot bypass the curve
cannot bypass the curve ![]() and
and ![]() in Figure 1(b). Let point
in Figure 1(b). Let point ![]() on
on![]() . Then:
. Then:
1) Point ![]() on
on ![]() in Figure 1(b) and,
in Figure 1(b) and,
2) Point ![]() on
on ![]() in Figure 1(c).
in Figure 1(c).
For part 1), let geodesic ![]() and
and ![]() on the outside of sector P, than the intersection of the G and
on the outside of sector P, than the intersection of the G and![]() . Notice that
. Notice that ![]() be a segment of geodesic
be a segment of geodesic![]() . With the same
. With the same ![]() on
on![]() , and also on
, and also on![]() , as in the
, as in the ![]() on
on![]() , and also on
, and also on![]() , then geodesic:
, then geodesic:
![]() . (2)
. (2)
So we conclude that ![]() on the outside of
on the outside of![]() . However, this is impossible.
. However, this is impossible.
For part 2), let![]() ,
, ![]() on geodesic
on geodesic![]() , with the same
, with the same ![]() on
on![]() , and also on
, and also on![]() , so the
, so the ![]()
![]() (a)
(a)![]() (b)
(b)![]() (c)
(c)
Figure 1. (a) The sector between the curve A and the curve U be a convex; (b) (c) The diagram showing that the sector P is convex; (b) Point F on GA; (c) Point F on GU.
of the geodesic ![]() replaced by the
replaced by the ![]() of the
of the![]() , as in all segment on geodesic
, as in all segment on geodesic![]() , substitute them completely, (in universal logic, the substitution principle we could use here) and though it is outside sector
, substitute them completely, (in universal logic, the substitution principle we could use here) and though it is outside sector![]() . Prove that
. Prove that ![]() is convex.
is convex.
Interpretations for the theorem: In this proof, we often went further than that, if using a parametric equation, such as the differential equation of the geodesic, only work on differential geometry―nothing else. As far as curve goes, we know, convex closed curve and circumference are homeomorphism. The shape of the curved surface, on the other hand, is associated with the curvature. If they exist, it as a point on the convex surface can be divided into three categories as its own characteristics, namely, smoothing-point (tangent cone is a plane), diamond-point (tangent cone is a dihedral), and cone-point (tangent cone is less than![]() ). Let
). Let ![]() be plane angle and let
be plane angle and let ![]() be dihedral, then
be dihedral, then![]() . So, the distortion of the convex polyhedron is predictable for us, by contrast, the galaxy can distort the space-time in which it sits. Beyond that, we may see integral geometry for the convex surface in sector
. So, the distortion of the convex polyhedron is predictable for us, by contrast, the galaxy can distort the space-time in which it sits. Beyond that, we may see integral geometry for the convex surface in sector![]() . We will continue to discuss on this sector as a top priority. But there is much more to it than that. What does it mean to say that a sector is convex surface? The convex sector is a curved universe, physically. It’s this curving of the fabric of the universe that gravitational waves are fluctuations in the curvature of space which propagate through the universe as gravitational waves, so outward from its source, and we feel as gravity. Meanwhile, that the light travels in curve lines is certain in the large-scale universe.
. We will continue to discuss on this sector as a top priority. But there is much more to it than that. What does it mean to say that a sector is convex surface? The convex sector is a curved universe, physically. It’s this curving of the fabric of the universe that gravitational waves are fluctuations in the curvature of space which propagate through the universe as gravitational waves, so outward from its source, and we feel as gravity. Meanwhile, that the light travels in curve lines is certain in the large-scale universe.
The convex two sectors ![]() and
and ![]() (Figure 1(b))―the malleable fabric whose geometry can be changed by the gravity of stars, planets and matter―was born.
(Figure 1(b))―the malleable fabric whose geometry can be changed by the gravity of stars, planets and matter―was born.
For the large-scale universe, we need to have a stable large-scale structure and critical cosmological angle because, candidly, the critical cosmological angle is possible in physics. Our standard from for the critical cosmological angle![]() , is
, is ![]()
In Figure 2(a) show the matter and dark matter for the cosmic angles![]() . This curved space
. This curved space ![]() is characterized by two properties:
is characterized by two properties:
3) If cosmic angles is ![]() (or
(or![]() ), then the universe is a closed universe in Figure 2(b).
), then the universe is a closed universe in Figure 2(b).
4) If cosmic angles is![]() , then the universe is a open universe in Figure 2(c).
, then the universe is a open universe in Figure 2(c).
Now we remark that for convex multiple sector, in general, we have the following laws.
2.2. All Angle Law
Let ![]() be a lattice angle (i.e. all angle), and let
be a lattice angle (i.e. all angle), and let![]() . Then
. Then
![]() . (3)
. (3)
2.3. Impossibility Law
If a lattice angle ![]() and around a point in convex sector, then for any a shortest distance (i.e. geodesic) shalt not go through the point (i.e. not sucked into the singularity).
and around a point in convex sector, then for any a shortest distance (i.e. geodesic) shalt not go through the point (i.e. not sucked into the singularity).
3. The Cosmic Laws
We could prove the existence of antimatter by cosmological argument, such as empty law:
![]() . (4)
. (4)
It is a spirit in the pointer type, but we will arrive at meaning empty set, and we will give the set identities of the physical meaning. The following physical laws illustrate the relationship of matter and antimatter.
3.1. Black Hole Law
Let ![]() be a black hole, and let A represent the matter sets, B represent the antimatter sets. If that is so, then
be a black hole, and let A represent the matter sets, B represent the antimatter sets. If that is so, then
![]() . (5)
. (5)
We’ve gotten to this point now: Our ![]() model for physics and explain observed phenomenon. It’s rare to find antimatter
model for physics and explain observed phenomenon. It’s rare to find antimatter ![]() in the large-scale universe
in the large-scale universe![]() , since it annihilates almost instantly when antimatter comes into contact with matter
, since it annihilates almost instantly when antimatter comes into contact with matter![]() . The
. The ![]() only occasionally appears in high-energy collisions. Antimatter comes
only occasionally appears in high-energy collisions. Antimatter comes
into contact with regular matter, the two annihilate, disappearing in a high-energy flash of light. But remember to follow the black hole law so you don’t inadvertently get yourself in trouble, and do some careful calculations (or operations).
Similarly, we can also illustrate the physical significance of![]() , we have the following physical law.
, we have the following physical law.
3.2. Universe Law
If the universe ![]() is compose of matter
is compose of matter ![]() and antimatter
and antimatter![]() , then
, then
![]() . (6)
. (6)
Interpretations for the universe law: The antimatter area is used to existing in universe. Actually, this black hole law and universe law mean matter and antimatter is independent existence, but they have relevance.
3.3. Natural Law (Mirror Image of U)
Antimatter is a mirror image of matter that is ![]() in Figure 3(a). Similarly, the universe is a mirror image of black hole (empty set) that is
in Figure 3(a). Similarly, the universe is a mirror image of black hole (empty set) that is ![]() in Figure 3(b).
in Figure 3(b).
Interpretations for the mirror image of U: In essence, understanding and controlling mirror images has led to the creation of many important matters. For every matter particle (say an electron, for example), a matching
antimatter particle is thought to exist (in this case, a positron) with the same mass, but an opposite charge. This is the physical evidence of illustrated matter and antimatter. From a molecular perspective, the atoms in certain molecules can often take up two different configurations that are mirror images (chirality) of each other. From the particle physics perspective, particles and anti-particles to abide by the black hole law (upon collision), the conversion of a PARTICLE and its corresponding antiparticle into pure electromagnetic ENERGY (called annihilation radiation). The mesons to abide by the Universe law (each containing a quark and an antiquark). Of course, a particle can be out of the event horizon to infinitely far away and to abide by the universe law.
3.4. Particle Law
If the black hole engulf the antiparticle![]() , then
, then
![]() (7)
(7)
where, the particle ![]() must become outgoing Hawking radiation [6] .
must become outgoing Hawking radiation [6] .
Interpretations for the particle law: So the matter-antimatter relationship is annihilation, yes, but it’s also a form of symbiosis.
3.5. Zero-Point Symbiosis Law
Let ![]() be matter, and let
be matter, and let ![]() be antimatter. If antimatter exist in symbiosis with matter, then
be antimatter. If antimatter exist in symbiosis with matter, then
![]() (8)
(8)
Interpretations for the zero-point symbiosis law: From this point of view, the relationship between matter and antimatter is more symbiotic, we call the process “zero-point symbiosis”.
3.6. Ideal Law (Minimal with Constraints i.e. End of Quantum Theory)
In principle, we exclaim the existence of the minimal matter (or minimal antimatter) in the universe, i.e. denoted
by![]() , and partially ordered structure denoted by
, and partially ordered structure denoted by![]() .
.
Interpretations for the ideal law: We show, in the ![]() case, without superpartners (or supersymmetry) quantum cosmology theory (or particle physics) does not exist, and this could be another major discovery in the sense that we would have to completely review completely our vision of universe.
case, without superpartners (or supersymmetry) quantum cosmology theory (or particle physics) does not exist, and this could be another major discovery in the sense that we would have to completely review completely our vision of universe.
3.7. Main Theorem (Non-Singular Point of U)
Let any![]() . Then
. Then
![]() . (9)
. (9)
Proof: By black hole law and particle law, we have
![]() . (10)
. (10)
The proof is complete.
In fact, we have got it all settled through the matter and the antimatter obey the same laws of physics, which is that the universe must be completely satisfying. So, the universe seems to be dominated by matter and not antimatter.
4. Conclusions
・ In attempting to explain the matter and antimatter, we have put forward the concept of axiom cosmology. Our “axiom” method is very simple, when in terms of some set operations we can write the theory in a very brief space, without a lot of complication, and the conclusions could be invaluable for the presence of dark matter and dark energy.
・ It is crucial for us to have a good understanding of the nature and results for the expansion of the universe. We raise a model touching the large-scale structure of the universe, so we begin to use it to explain cosmological mysteries of closed universe or open universe. As such, the axiom cosmology is one path to the final theory.
・ What matters is that cosmological set operations we have seen have played as a tool for cosmic research. In particular, we propose to solve the problem of physical singularity in space-time, which is full of infinite axiom cosmology charms and vitality.
Acknowledgements
The author is grateful to the anonymous referees for useful comments and suggestions.