The Influence Function of the Correlation Indexes in a Two-by-Two Table ()
1. Introduction
In this paper we analyze the influence of a minimal contamination of the bivariate Bernoulli distribution on the values of the index measuring the association in a two-by-two table, having as a scenario the estimation of the correlation parameter of that distribution.
2. Bivariate Bernoulli Model
Selecting a Template
Let us suppose that two dichotomous variables, denoted by X and Y, are relevant within a population. These variables take the values 1 and 0, depending on whether one of the dichotomous attributes is present or absent. The corresponding theoretical model is the bivariate Bernoulli distribution [1] , reported in Table 1.
The mean values of the two variables are
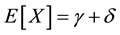 , (1)
, (1)
 . (2)
. (2)
The variances of the two variables are
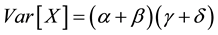 , (3)
, (3)
 . (4)
. (4)
The covariance between the two variables is
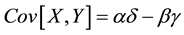 . (5)
. (5)
The correlation coefficient is
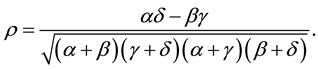 (6)
(6)
3. Properties of the Correlation Parameter Estimation
Several indexes, suggested by various authors (Yule, Quetelet and others), are available for the sample estimation of the above-mentioned correlation coefficient. We refer to such indexes as R1, R2 etc. For given indexes, Rh, all variable between −1 and +1, we must take into account unbiasedness, i.e.
 (7)
(7)
efficiency, i.e.
 , (8)
, (8)
and the limited influence of limited modification of the model.
With regard to this last fundamental property Hampel [2] in 1974 suggested the influence function as a tool for evaluating the effect caused on the value of an indexby a minimal contamination of the model. In our case the model is the bivariate Bernoulli distribution, the parameter is the correlation coefficient 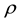 and the indexes are those proposed by various authors over time.
and the indexes are those proposed by various authors over time.
Basically the influence function  referred to the index R is given by
referred to the index R is given by
 , (9)
, (9)
where 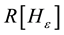 is the index computed for the contaminated bivariate Bernoulli distribution
is the index computed for the contaminated bivariate Bernoulli distribution ,
,  is the
is the
![]()
Table 1. The bivariate Bernoulli distribution.
index computed for the non-contaminated bivariate Bernoulli distribution and 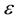 is the weight of the contamination.
is the weight of the contamination.
It is easily understood that such a function measures the effect of an infinitesimal contamination of the model on the value of the correlation index [3] . From now on we will denote by a, b, c and d the empirical frequencies of the four cells of the two-by-two table obtained for a sample of n units.
4. Influence Function of the Correlation Indexes
4.1. C Index
Let us first consider the elementary index given by
![]() (10)
(10)
A contamination in the cell (0,0) leads to the influence function value
![]() (11)
(11)
while a contamination in the cell (1,1) leads to the influence function value
![]() (12)
(12)
That is, a contamination in one of the two cells indicating concordance increases the value of the C index of a quantity, which is proportional to the sum of the frequencies of the two discordance cells.
A contamination in the cell (0,1) leads to the influence function value
![]() (13)
(13)
while a contamination in the cell (1,0) leads to the influence function value
![]() (14)
(14)
That is, a contamination in one of the two cells indicating discordance decreases the value of the C index of a quantity, which is proportional to the sum of the frequencies of the two concordance cells.
In short, the influence function can be displayed as
![]() , (15)
, (15)
in which v, in the case of a concordance cell, is equal to the sum of the discordance frequencies, while, in the case of a discordance cell, is equal to the sum of the frequencies of discordance cells, changed of sign. In other words, the influence of the contamination for each concordance cell is directly proportional to the sum of the discordant frequencies and vice versa, for each discordance cell, provided that it is positive for the concordance cells and negative for the discordance cells [4] .
4.2. Yule’s Q Index
Let us first consider the 1900 Yule’s index [5] given by
![]() (16)
(16)
A contamination in the cell (0,0) leads to the following value of the influence function
![]() (17)
(17)
while a contamination in the cell (1,1) leads to the value given by
![]() (18)
(18)
That is, a contamination in one of the two cells indicating concordance increases the value of the index Q by a quantity, which is proportional to the product of the frequencies of the three non-contaminated cells.
On the other hand a contamination in the cell (0,1) leads to the value of the influence function given by
![]() (19)
(19)
while a contamination in the cell (1,0) leads to the following value of the influence function
![]() (20)
(20)
That is, a contamination in one of the two cells indicating discordance decreases the value of the index Q by a quantity, which is proportional to the product of the frequencies of the three non-contaminated cells.
In short, the influence function can be displayed as
![]() (21)
(21)
in which v is equal to one of the frequencies with positive sign if it corresponds to a or to d, and to one of the frequencies with negative sign if it corresponds to b or to c. In other words, the influence of the contamination is inversely proportional to the frequency of the contaminated cell, provided that it is positive for the concordance cells and negative for the discordance cells.
4.3. Yule’s Y Index
Let us consider now the other index proposed by Yule [6] in 1912,
![]() . (22)
. (22)
A contamination in the cell (0,0) leads to the following value of the influence function
![]() (23)
(23)
while a contamination in the cell (1,1) leads to the value of the influence function given by
![]() (24)
(24)
That is, a contamination in one of the two cells indicating concordance increases the value of the index Y by a quantity proportional to the root of the product of the frequencies of the three non-contaminated cells divided by the root of the frequency of the contaminated cell.
A contamination in the cell (0,1) leads to the value of the influence function given by
![]() (25)
(25)
while a contamination in the cell (1,0) leads to the following value of the influence function
![]() (26)
(26)
That is, a contamination in one of the two cells indicating discordance decreases the value of the index Y by a quantity proportional to the root of the product of the frequencies of the three non-contaminated cells divided by the root of the frequency of the contaminated cell.
In short, the influence function can be displayed as
![]() (27)
(27)
in which v is equal to one of the frequencies with positive sign if a or d and to one of the frequencies with negative sign if b or c. In other words, the influence of the contamination is inversely proportional to the frequency of the contaminated cell, provided that it is positive for the concordance cells and negative for the discordance cells.
4.4. The Chi Square Index
Let us examine the chi square index
![]() (28)
(28)
A contamination in the cell (0,0) leads to the influence function value
![]() (29)
(29)
while a contamination in the cell (1,1) leads to the influence function value
![]() (30)
(30)
That is, a contamination in one of the two cells indicating concordance increases the value of the ![]() by a quantity which is proportional to the product of the sums of the frequency of the other concordance cell with each of the frequencies of the discordance cell.
by a quantity which is proportional to the product of the sums of the frequency of the other concordance cell with each of the frequencies of the discordance cell.
A contamination in the cell (0,1) leads to the influence function value
![]() (31)
(31)
while a contamination in the cell (1,0) leads to the influence function value
![]() (32)
(32)
That is, a contamination in one of the two cells indicating discordance decreases the value of the ![]() by a quantity which is proportional to the product of the sums of the frequency of the other discordance cell with each of the frequencies of the concordance cells.
by a quantity which is proportional to the product of the sums of the frequency of the other discordance cell with each of the frequencies of the concordance cells.
It is impossible to have a unique expression of the influence function as we had for the other indexes, because the expressions for the contaminated concordance cells differ from those related to the discordance ones.
4.5. Odds Ratio, θ
Let us now examine the odds ratio index
![]() (33)
(33)
A contamination in the cell (0,0) leads to the influence function value
![]() , (34)
, (34)
while a contamination in the cell (1,1) leads to the influence function value
![]() (35)
(35)
That is, a contamination in one of the two cells indicating concordance increases the value of the index ![]() by a quantity that is proportional to the frequency of the other concordance cell and inversely proportional to the product of the frequencies of the discordance cells.
by a quantity that is proportional to the frequency of the other concordance cell and inversely proportional to the product of the frequencies of the discordance cells.
A contamination in the cell (0,1) leads to the influence function value
![]() (36)
(36)
while a contamination in cell (1,0) leads to the influence function value
![]() (37)
(37)
That is, a contamination in one of the two cells indicating discordance decreases the value of the index ![]() by a quantity, which is proportional to the product of the frequencies of the concordance cell and inversely proportional to the product of the square of the frequency of the contaminated cell multiplied by the frequency of the other discordance cell.
by a quantity, which is proportional to the product of the frequencies of the concordance cell and inversely proportional to the product of the square of the frequency of the contaminated cell multiplied by the frequency of the other discordance cell.
In short, the influence function can be displayed as
![]() (38)
(38)
in which v is equal to the frequency of the contaminated cell, provided that the sign is positive in case of contamination in a concordance cell, and negative in case of contamination in a discordance cell.
5. Unbiasedness of the Indexes
It must be reminded that an index ![]() is unbiased if
is unbiased if
![]() (39)
(39)
let us examine now the unbiasedness of every index.
5.1. The Chi Square Index
The index
![]() (40)
(40)
has the mean
![]() (41)
(41)
and therefore it is unbiased.
5.2. Other Indexes
Indexes Q, Y, θ e C are biased.
It has to be said that 3 of the considered indexes (Q, Y and θ) are functionally related, as it is shown below:
![]() ,
, ![]() for
for ![]() and
and ![]() for
for![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , for
, for ![]() and
and![]() , for
, for![]() .
.
The other 2 indexes (C and![]() ) are not functionally explainable with themselves nor with the above-men- tioned ones. The 5 indexes estimate functions of the
) are not functionally explainable with themselves nor with the above-men- tioned ones. The 5 indexes estimate functions of the ![]() parameter. More exactly 4 of these indexes (C, Q, Y and
parameter. More exactly 4 of these indexes (C, Q, Y and![]() ) are estimators of increasing functions of this parameter and, in particular in the points −1, 0 and +1, these functions coincide with the argument. So the index
) are estimators of increasing functions of this parameter and, in particular in the points −1, 0 and +1, these functions coincide with the argument. So the index ![]() can easily lead to the 2 Yule’s indexes achieving again its characteristics.
can easily lead to the 2 Yule’s indexes achieving again its characteristics.
6. Influences of the Indexes
Since that the effects of contaminations in the various cells are balanced, it is necessary to evaluate their overall influence regardless of the sign. This can be done considering the maximum of the absolute values of the influence or the mean absolute deviation or the variance of the said values [7] .
6.1. Maximum of the Absolute Values of the Influence Function (Gross Sensitivity Error)
6.1.1. C Index
As, regardless of the sign, the influence function is equal to
![]() , (42)
, (42)
the maximum of the influence function is therefore
![]() . (43)
. (43)
6.1.2. Yule’s Q Index
As, regardless of the sign, the influence function is equal to
![]() , (44)
, (44)
in which v is one of the four frequencies of the table, the maximum of the influence function is obtained for min(v); it is therefore
![]() (45)
(45)
6.1.3. Yule’s Y Index
As, regardless of the sign, the influence function is equal to
![]() , (46)
, (46)
in which v is one of the four frequencies of the table, the maximum of the influence function is obtained for min(v); it is therefore
![]() (47)
(47)
6.1.4. Chi Square Index
An empirical analysis allows to asses that the maximum absolute value of the influence function is obtained in correspondence of the minimum frequency. Thus,
![]() (48)
(48)
![]() (49)
(49)
![]() (50)
(50)
![]() (51)
(51)
6.1.5. Odds Ratio
As, regardless of the sign, the influence function is equal to
![]() , (52)
, (52)
in which v is one of the four frequencies of the table, the maximum of the influence function is obtained for min(v); it is therefore
![]() (53)
(53)
6.2. Variability of Influence Functions: Mean Absolute Deviation
6.2.1. C Index
A few algebraic steps allow us to obtain
![]() . (54)
. (54)
6.2.2. Yule’s Q Index
![]() (55)
(55)
6.2.3. Yule’s Y Index
![]() (56)
(56)
6.2.4. Chi Square
![]() (57)
(57)
6.2.5. Odds Ratio
![]() (58)
(58)
It can be seen that the mean deviation for all indexes is a symmetric function either of the concordant frequencies or of the discordant frequencies.
6.3. Variability of the Influence Function Asymptotic Variance (A.S.V.)
6.3.1. C Index
Let us consider the asymptotic variance of the indexes. A few algebraic steps lead us to the following expression
![]() (59)
(59)
6.3.2. Yule’s Q Index
![]() (60)
(60)
6.3.3. Yule’s Y Index
![]() (61)
(61)
6.3.4. Chi Square Index
![]() (62)
(62)
6.3.5. Odds Ratio
![]() (63)
(63)
It can be seen that the asymptotic variance is a symmetric function of the concordance and discordance frequencies as well.
7. Example
Let us consider a practical example in which 1071 persons are classified on 2 dichotomic characters: “does he/she smoke” and “is he/she suffering from bronchitis?” both with yes or no response (see Table 2).
There were 1071 cases of which 135 smoke and have bronchitis and 547 don’t smoke and don’t have bronchitis.
As it can be noticed, between the 4 indexes whose values go between −1 and +1, the ones which are less sensitive to contamination are C and chi square indexes; on the other hand, the more sensitive ones are Yule’s indexes, Q and Y. The greater sensitivity of the odds ratio is due to the fact that such index measures a function of the correlation of the model that goes in the range from 1 to ¥.
Source: Survey at the University Hospital of Bari, Department of Pulmonology.
8. Conclusions
In this paper we analyzed the indexes of a two-by-two table, which allow the estimation of the correlation coefficient ρ in the bivariate Bernoulli model. More precisely, we considered the two Yule’s indexes, the chi square, the odds ratio and a further elementary index. We obtained, for these indexes, the compact expressions of the influence functions, which allow the quantification of the effect of an infinitesimal contamination of the probability of any pair of attributes of the bivariate random variable distributed according to the above-mentioned model.
In order to determine the indexes which are less sensitive to contamination, we obtained the expressions of three synthetic measures of the influence function, specifically the maximum contamination (gross sensitivity error), the mean absolute deviation and the variance. These expressions, even if don’t allow a definitive assessment of the overall optimum properties of the five indexes considered, as not all of them are unbiased, nevertheless they allow to appreciating the synthetic entity of the effect of the contaminations in the estimation of the parameter ρ of the bivariate Bernoulli model.
NOTES
*The paragraphs 1 and 2 are attributed to G. Girone, the paragraphs 3, 4 and 8 to F. Manca and the paragraphs 5, 6 and 7 to C. Marin.