The Optimal Hedge Ratio in Option Pricing: The Case of Exponentially Truncated Lévy Stable Distribution ()
1. Stable Lévy Processes in Options Pricing
Stable Levy processes played a particular role in the evolution of financial knowledge since they were the first theoretical alternative to Gaussian framework for the statistical description of financial leptokurticity [1] -[4] . In the past decade or so, we observe an explosion in the literature related to stable Levy processes as detailed in Tankov [5] . There are two methodological ways of applying these processes in finance: the vast majority of empirical works dealing with stable Levy processes in finance are based on a conditional approach decomposing the description of empirical data into two distributions: the first distribution is said unconditional (often assumed Gaussian) and it describes the historical data while the role of the second distribution is to characterize the evolution of volatility for which the occurrence of extreme value cannot be explained in Gaussian terms. This methodological decomposition allows financial modellers to consider that current fluctuations are more sensitive to recent ones (short memory property also called “volatility clustering” in finance). In this perspective, stable Levy processes are only applied for the conditional distribution characterizing the evolution of volatility (i.e. fat- tail part) and not for describing the whole empirical distribution.
The second way of implementing stable Levy processes in finance is to associate them with a unique and unconditional distribution capturing empirical data. This methodological perspective has mainly been developed by econophysicists who often emphasised the advantage of dealing with historical data: studying financial data as they appeared in the past (and not as they should be according to a pre-existing theoretical framework) allows modellers to develop a less biased estimation of risk (McCauley, 2004; Famer and Geneakoplos, 2008). However, although empirical evidence suggesting the use of stable Levy processes for describing financial data, the theoretical properties of these processes imply an infinite variance which did not favour their empirical application. Indeed, an infinite variance property means it is not possible to value the major risk parameter (volatility) used in finance making obsolete all classical perspective of risk management. In the same vein, an infinite variance of financial prices leads to an impossibility to price financial assets since their variance would not converge toward a finite value. This situation makes stable Levy processes very interesting in knowledge because they required a specific statistical treatment to make them “applicable” in assets pricing. These treatments generated a lot of debates in the 1960s and 1970s [6] and no consensus, at that time, emerged on the way of integrating these processes into financial economics. Consequently, financial economists developed some strategies [7] [8] in their unconditional use of stable Levy processes for options pricing.
Roughly speaking, the unconditional application of stable Levy processes in options pricing can be decomposed into through three categories of models which can be identified depending on the technical solution developed to escape from the infinite variance problem: i) time-changed processes; ii) models using a specific calibration of parameters and iii) models based on a particular calibration (truncation) of the distribution. The first category refers to time-changed models which introduce an “intrinsic time” (for options’ underlying) providing tail effects as observed in the market. Examples of these models are contained in Mandelbrot et al. [9] ; Hurst, Platen and Rachev [10] ; Geman, Madan and Yor [11] or Carr and Wu [12] . Within this framework, the leptokurticity of empirical distributions is generated by a stable Lévy process-time subordinated to the Wiener process. In other words, the variance of options’ underlying is still assumed finite since the stable Levy processes are only applied for characterizing time distribution for which a variance analysis becomes therefore irrele- vant since the “variance of time” has no financial meaning. Concretely, the physical time in the Gaussian frame- work is substituted by an intrinsic time characterized by a non-negative subordinated process: if 
is a Wiener process and 
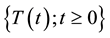a non-negative stochastic process, then the new time process subordinated
to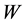 
will be
.
The second category of models refers to a specific calibration of parameters in order to have finite statistical moments for the processes describing the options’ underlying distribution. Empirical distributions or time are not changed but authors give specific statistical conditions implying the existence of all statistical moments. In this framework, modellers defined specific conditions implying the possibility for variance to converge toward a finite value. Carr and Wu ( [13] , for example, developed an option pricing theory based on a log stable process with a specific calibration of the skewness in order to have finite moments. See also McCulloch [14] , Borland [15] or Cartea et al. [16] for other examples of models in this category.
The third category of statistical solutions (within this article) developed to solve the problem of infinite variance, refers to all models based on a particular calibration of the whole distribution. That approach is well known by econophysicists who developed several truncation techniques in order to capture the fat-tailed distribution with an unconditional approach and a finite variance [17] . This way of using stable Levy processes required the definition of a truncation function, Matacz [18] and Boyarchenko and Levendorskii [19] [20] offered an interesting option pricing model based on an exponential truncated stable Levy distribution. However, although these authors gave a procedure to minimize an estimated risk, they did not define the conditions for a potential optimal risk hedge. At the opposite, McCauley et al. [21] , for example, showed that a no-Gaussian option pricing model can provide an optimal risk hedging but their model focused on general conditions without defining an individual cut-off. Significantly, this existing literature does not directly address the implications of truncated exponential Levy models for the optimal option hedge ratio problem. However, this is of interest in an econophysics context due to various contributions stretching back to studies by Mantegna and Stanley in the mid-1990s that employed truncation to deal with statistical limitations of “infinite variance”.
This paper aims to define the minimal condition required for an optimal risk hedging for a particular cut-off based on an exponentially truncated stable Lévy distribution. In other words, our contribution is to show that a (no-conditional) exponential stable Lévy description of a financial distribution (i.e. description of the whole distribution) can admit an admissible hedging strategy in a sense defined by Harrison and Kreps [22] and Harrison and Pliska [23] who showed that the existence of an equivalent martingale measure was a necessary condition for an optimal hedging (see Carr and Madan [24] for further details on that theme).
While the first section will present our generalized model in line with the Black and Scholes framework (based on a martingale measure), the second section will define a specific risk measure for a stable Levy version of this model that we will present in the third section. In line with [21] , we will use an exponentially truncated stable Lévy distribution whose statistical conditions will be defined to make this model viable (i.e. meeting the necessary condition) in a sense suggested by Harrison and Kreps [22] .
2. The Model
Let’s consider a portfolio made up of a (call) option and a short position on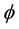 
stocks. At time
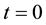, the value of this portfolio 
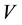is: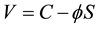 
where C is the price of the call option (with strike price K and expiration T); S is the stock price and 
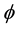is the quantity of the stock. The product 
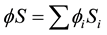is to be seen as a scalar product with Si the price for each stock. Initially the stock price is considered to be 
and the portfolio is considered to be self-financing. In other words the value of the portfolio changes only due to changes in the stock price. In this situation the variation of the portfolio between time t = 0 and T is given by: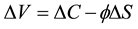
. The variation of the portfolio due to the call option is, when continuously discounted at the risk free rate r:
(1)
where the first term is the value of the option at time T and the second term is the premium paid for the option at time
. Assuming, we operate in a no-arbitrage market then the discounted stochastic price process must be a martingale (Harrison and Kreps, [22] ). We get for the option price:
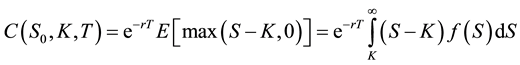(2)
Due to the stochastic nature of the price process, risk is inherent to the financial evaluation of options and stocks. For the log-normal distribution it was shown by Black and Scholes [25] that this risk can be hedged by using an appropriate hedging condition (the so-called f hedging) for the financing strategy. But for non-normal models, the Black and Scholes procedure for hedging risk does not work anymore1. A measure of risk that was also used in Bouchaud and Sornette [26] and Aurell et al. [27] is the variance of the value of the portfolio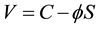
. We make the supposition here that this variance is finite2. Thus:
![]()
(3)
First of all let us note that for uncorrelated assets, we have the following expression:
![]()
where ![]()
is the volatility. However, when there exists a correlation between the assets, we can write, ![]()
where ![]()
is the covariance matrix. In a sense,
our conceptual model defined in Equation (3) is in line with the generalized call option pricing formula defined by Tan [28] in which S is observed for non-gaussian distributions. This approach is well-known in finance and it requires a minimization of the risk with respect to the trading strategy:
![]()
(4)
This equation is valid for a martingale process ![]()
with ![]()
ensuring the necessary condition for having an optimal hedging solution. If there are more than one uncorrelated assets (stocks) the above equation should be applied for each stock individually in order to get the total optimal hedging strategy. The optimal strategy for the![]()
’th asset would be written like the above equation with index ![]()
on all variables (expect thus
![]()
). For many correlated assets using![]()
, one finds:
![]()
(5)
In the simplest case, it is straightforward to observe that in the case of the normal distribution with log-returns the optimal hedging strategy given in Equation (4) is the same as the hedging strategy from the Black and Scho-
les model, i.e.![]()
. The minimal risk ![]()
corresponding to the optimal hedging strategy is obtained from
Equation (3): ![]()
for one stock. Note that ![]()
is a risk term not-dependent upon the investment
strategy, defined as![]()
. In the general case with many correlated assets, the minimal risk is obtained by taking ![]()
into account. Bouchaud and Sor-
nette [26] showed that ![]()
vanished when a log-normal density is used. In other words, the Equation (4) provides a martingale-based risk measure which must be minimized in an incomplete market structure.
3. Hedging Strategy with Exponentially Truncated Lévy Stable Distribution
As previously mentioned, stable Levy framework generates infinite variance, therefore a no computable risk leading authors to find a solution: while Tan [28] developed a generalized call option pricing formula by implicitly assuming a finite variance (making stable Lévy processes inappropriate within his model), McCauley et al. [21] showed the general conditions for an optimal hedging with no-Gaussian option pricing model without defining a specific cut-off for the fat-tails distribution.
This section focuses on a particular cut-off based on an exponentially truncated stable Lévy process for option pricing by determining conditions for which the risk measure defined in the previous section can be viable in a hedging framework developed by Harrison and Kreps [22] (i.e. risk measure for our model is based on a martingale). We plan to integrate our model in the generalized formula provided by Bucsa et al. [29] in their review of literature about Levy processes used in econophysics. These authors proposed the following generalized formula to characterize the use of stable Levy processes in econophysics:
![]()
(6)
The number of parameters refers to the great diversification of models developed in the econophysical literature3. In other words, all existing use of stable Levy processes (included the Gaussian one) in econophysics can be seen as a specific case of this generic equation.
In line with the central limit theorem, a stable Levy regime will converge4 toward a Gaussian asymptotic distribution after a very high number of variables![]()
. In other words, there is a cross-value ![]()
after which the stable Levy process is supposed to switch into the asymptotic (Gaussian) regime.That particular evolution implies a Gaussian asymptotic regime for ![]()
and a truncated stable regime for![]()
. While the first can also be seen
as a specific case of the generic Formula (6) with the following parameters, ![]()
, ![]()
,
![]()
, ![]()
and![]()
; The latter can be described through the following specific case where
distribution density for the log returns of options underlying can take the following form,
![]()
where![]()
, ![]()
, ![]()
and ![]()
which is the condition to have a stable Levy distribution (See Bucsa et al. [29] ). ![]()
can be seen as a measure of the level of activity in case all other parameters are constant (i.e. a parameter of scale). The parameter ![]()
is the speed at which arrival rates decline with the size of the move (i.e. rate of exponential decay). This model is in line with works dealing with exponential truncation exposed by Schinckus [17] and this formula is a symmetric version of the so-called CGMY model (Carr et al. [31] ) and a generalization of the exponentially truncated Lévy stable models proposed by Koponen [32] or Boyarchenko and Levendorskii [19] [20] . However, while the first authors applied this model in a time changed framework, Koponen [32] did not apply his model to options pricing whereas Boyarchenko and Levendorskii [19] [20] did not seek conditions for a potential risk hedge. Our objective in this paper is to show that the stable Levy regime (with no time-changed distribution) is theoretically in line with a key assumption of the mainstream characterization evolution of the options’ underlying―in this perspective, we deal now only with the stable Levy regime whose use can be justified by the necessity to deal with short-term information (for which a Gaussian regime does not occur) in portfolio management.
Because stable Lévy processes generate infinite variance, we use an exponentially truncation implying an exponential decay of the distribution. This restriction means that the truncated distribution generates finite variations making possible the estimation of the variance (in the stable Levy regime) which is given by the following equation:
![]()
(7)
Using the general Equation (2) we calculate the option price for this model for the chosen portfolio, by considering the density distribution of stock returns:
![]()
(8)
Using the result ![]()
with ![]()
in Equation (8), and expressing ![]()
as a function
of squared volatility, yields:
![]()
(9)
Given this result, we can estimate the hedging strategy minimizing the risk by using Equation (4):
![]()
(10)
However, this optimal hedging can be implemented in the non-asymptotic regime implying that the variance
(Equation (7)) is finite only for x < l. By integrating![]()
, we can rewrite the Equation (10) as:
![]()
(11)
Although Tan [28] did not deal with infinite variance processes, we found the same conclusions about non- Gaussian densities, ![]()
, which explicitly depend on i) higher partial derivatives of the call option pricing function towards the price of the underlying asset; and ii) the value of the cumulants (as they are used in the logarithm of the characteristic function). Although this Equation (11) can then be possibly further generalized as proposed by McCauley et al. [21] or Tan [28] , this generalization required specific statistical conditions defined in this paper in order to offer a viable hedging solution in a stable Levy framework. The objective of this article was to show the theoretical compatibility between an exponentially truncated stable Levy framework and the necessary condition for an optimal hedging in the financial mainstream―the next step of this research will be to explore empirical dimension of that condition by doing parametric plots and comparing with alternative possible models.
4. Conclusion
This article defined conditions for which an option pricing model based on an exponentially truncated stable Lévy distribution can be viable in a Harrison and Kreps [22] framework. Although the uniqueness of this martingale is not obvious for stable Lévy processes, the exponential truncation combined with the symmetry condition ensures the condition for the existence of at least one martingale measure. In this perspective, our pricing model is in line with the necessary condition (but not with the sufficient condition) defined by Harrison and Kreps [22] in order to have an optimal hedging. This paper shows that, from a theoretical point of view, an unconditional use of stable Lévy framework can make sense in the financial mainstream.
NOTES
*Corresponding author.
![]()
1That point is important since it refers the incompleteness of markets.
2Because we work unconditionally on the whole distribution (and not only on the fat-tail part of the distribution), we do not have to define a short-term time dependence for the variance as it is usually done in conditional methodology such as ARCH types models.
![]()
3Although, in the great majority of the models a1, b1 = 1; b2 and d are equal to zero―See Bucsa et al. [29] .
4It is worth mentioning that this convergence of x to a Gausian regime is extremely slow due to the stable property of the Levy distribution [8] . The crossover value Nc can be derived by using Berry-Esseen Theorem [30] or by using a method based on the probability of x returning to the origin [8] ―both approaches provide a crossover value equal to ![]()
where c is the scale factor and l the cross-value at which the regime will switch from a stable Levy to a Gaussian one.