1. Introduction
Probability distributions defined by graphs are used in literature of various fields, such as coding theory, artificial intelligence, and system theory.
LDPC [1] code can be depicted by its parity-check matrix H [2] ,  and its degree distribution of polynomial [3] :
and its degree distribution of polynomial [3] :
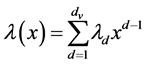 (1)
(1)
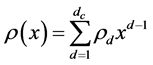 (2)
(2)
Computing distributions of variable and check nodes in a Tanner graph is relatively efficient without cycle, but complex with cycles, even difficult when cycles are short for large graph.
The belief propagation algorithm [4] , or known as the sum-product algorithm [5] is decoding algorithm for graphical codes, such as convolution code, turbo code and LDPC code.
Belief propagation (BP) algorithm is optimal and produces exact solutions on a tree just in a finite number of iterations. Otherwise, BP algorithm may not converge. Moreover, when it doses converge, it provides approximate solution and the results vary in different conditions.
2. Background
In most common sense of the term, an undirected graph [6] consists of a set of vertices or nodes V together with a set of edges E, which are 2-element subsets of V (i.e., an edge is related with two vertices, and the relation is represented as an unordered pair of the vertices with respect to the particular edge). See Figure 1.
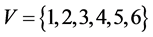

n = 6
m = 5
Let  be an undirected graph.
be an undirected graph.
The following statements are equivalent,
1. G is a tree
2. Any two vertices in G are connected by a unique simple path
3. G is connected, but if any edge is removed from E, the resulting graph is disconnected
4. G is connected, and 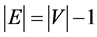
5. G is acyclic, and 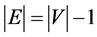
6. G is acyclic, but if any edge is added to E, the resulting graph contains a loop.
In fact, a tree is a connected graph without any cycles; a leaf is a vertex of degree 1. An internal vertex is a vertex of degree at least 2.
In coding theory, Tanner graph, named after Michael Tanner, is a bipartite graph used to state constraints or equations which specify error correcting codes. See Figure 2. They are used to construct longer codes from smaller ones. Both encoders and decoders employ these graphs extensively.
![]()
Figure 2. Tanner graph of an LDPC code (a cycle represented by 4 bold lines in figure).
In communication system, the transmitted random vector 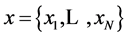 is not observed; instead received noisy vector
is not observed; instead received noisy vector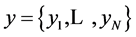 .
.
N is the length of codeword, Parity check equation vector is , M is the number of equations.
, M is the number of equations. 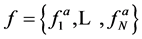 represents initial information about transmitted codeword.
represents initial information about transmitted codeword.
where, 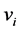 is the ith variable node,
is the ith variable node, ![]() , jth check equation.
, jth check equation.
The belief propagation (BP) of LDPC code states as follows [7] - [11] :
![]() is check information from check node
is check information from check node ![]() to variable node
to variable node![]() , and
, and ![]() variable information from
variable information from ![]() to check node
to check node![]() . See Figure 3.
. See Figure 3.
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
where ![]() denotes a normalization constant,
denotes a normalization constant,![]() . And message updating rule see Figure 4 [12] .
. And message updating rule see Figure 4 [12] .
![]()
Figure 4. Updating rule for message passing.
3. Principle of Cut-Node Tree
In order to solute loops of LDPC code, Tanner graph is re-drew as following principle: Choosing an element “1” in H, its variable (or check) node considered root node, check (or variable) nodes connected to the variable (or check) node as 1st order child-nodes, a current node, once appearance in ancestor node or sibling node, will be cut and forbid to grow and become a end node like a leaf, but not a leaf actually. And so forth, at last a cut-node tree can be get. If all nodes are connected, a single cut-node tree can be get, otherwise it is forest. Repeating this process until all end nodes are either cut-node or leaf node. See Figure 5.
HH is mark matrix, every element in HH is zero represents end of algorithm.
![]()
Figure 5. Flow process chart of algorithm.
4. Implement of Principle and Results
First, a node (variable node or check node), for instance, variable node![]() , is choosed as root node, its son nodes are those which connect to it, according to this principle, we can obtain all child-nodes. This process can be implemented by computer simulation in matlab’s celluar array, and express H by means of cut-node tree.
, is choosed as root node, its son nodes are those which connect to it, according to this principle, we can obtain all child-nodes. This process can be implemented by computer simulation in matlab’s celluar array, and express H by means of cut-node tree.
An example: for
![]() (7)
(7)
has following cut-node tree graph (Figure 6).
Another example: For instance, an LDPC code with check matrix H:
![]() (8)
(8)
Following tree matrix expressed by matlab can be get:
![]() (9)
(9)
In fact, tree matrix matches along with Tree of Graph, [i j k l m], [i j] states current node, [k l] states father node, m states times being cut.
So, searched by a computer, all loops can be get:
Loop 1: [4 8]-[3 8]-[3 5]-[2 5]-[2 6]-[4 6]-[4 8]
Loop 2: [5 9]-[3 9]-[3 5]-[2 5]-[2 7]-[5 7]-[5 10]
Loop 3: [5 10]-[4 10]-[4 6]-[2 6]-[2 7]-[5 7]-[5 10]
Loop 4: [1 1]-[1 2]-[3 2]-[3 5]-[2 5]-[2 1]-[1 1]
Loop 5: [1 3]-[1 2]-[3 2]-[3 5]-[2 5]-[2 6]-[4 6]-[4 3]-[1 3]
Loop 6: [1 4]-[1 2]-[3 2]-[3 5]-[2 5]-[2 7]-[5 7]-[5 4]-[1 4]
Loop 7: [1 1]-[1 3]-[4 3]-[4 6]-[2 6]-[2 1]-[1 1]
Loop 8: [1 1]-[1 3]-[4 3]-[4 6]-[2 6]-[2 5]-[3 5]-[3 2]-[1 2]-[1 1]
Loop 9: [1 4]-[1 3]-[4 3]-[4 6]-[2 6]-[2 5]-[3 5]-[3 2]-[1 2]-[1 4]
Loop 10: [1 4]-[1 3]-[4 3]-[4 6]-[2 6]-[2 7]-[5 7]-[5 4]-[1 4]
Loop 11: [1 1]-[1 4]-[5 4]-[5 7]-[2 7]-[2 1]-[1 1]
Loop 12: [1 1]-[1 4]-[5 4]-[5 7]-[2 7]-[2 5]-[3 5]-[3 2]-[1 2]-[1 1]
Loop 13: [1 1]-[1 4]-[5 4]-[5 7]-[2 7]-[2 6]-[4 6]-[4 3]-[1 3]-[1 1]
Loop 14: [1 2]-[1 4]-[5 4]-[5 7]-[2 7]-[2 5]-[3 5]-[3 2]-[1 2]
Loop 15: [1 2]-[1 4]-[5 4]-[5 7]-[2 7]-[2 6]-[4 6]-[4 3]-[1 3]-[1 2]
Loop 16: [1 3]-[1 4]-[5 4]-[5 7]-[2 7]-[2 5]-[3 5]-[3 2]-[1 2]-[1 3]
Here, H is just a situation of single tree, with 15 cut-nodes, no leaf node and 16 loops. See Table 1. Further, Message-passing form for cut-node tree has following rule:
In a tree, Message-passing fellows a two-pass form, first sweeping upwards from leaves to a node designated as the root, and then downwards from the root to leaves.
In a graph with cycle, Cut-node tree graph can be get by cutting all loops, See Figure 7.
Cut node tree has all same characters with Tanner graph.
![]()
Figure 7. Message passing over cut-node tree graph.
![]()
Table 1. Features of loops about above example.
5. Conclusion
This paper provides a new method to describe graph of LDPC codes, it aims to solute loops of LDPC codes and message passing over cut node tree. For a large matrix H, it is difficult to solute loops, because loops convolve each other. Features of loops have certain relationship with performances. In this paper, a cut node tree can be expressed by a certain matrix. By computer simulation, cut-node tree can get right answer and give out method to calculate loops of LDPC codes and cut node tree graph, its results assist to further research this relationship.