Conventional and Added-Order Proportional Nonlinear Integral Observers ()
1. Introduction
State observer design plays an essential role in the design of control system. Compared with most type of observers, the Proportional and Integral (PI) observers as an extension of Luenberger’s observer [1] have attracted considerable attention over the past 30 years. By using the integral information as an additional degree of freedom, PI observers can significantly improve the estimation error dynamics. Thus, the design and application of PI observer remain an interesting research topic.
The PI observer was first proposed by [2] for single input single output linear time-invariant system. After that, PI observers for linear multivariable time-varying system [3] , linear systems with unknown input disturbances [4] , linear uncertain system [5] , descriptor system [6] [7] , respectively, appeared. However, all of PI observers were designed by proportional to a linear integral of the output estimated error. Presently, P_NI observers have not been developed.
The observers for nonlinear uncertain systems mainly focus on particular classes of nonlinear systems. For the class of Lipschitz nonlinear system, an observer [8] was proposed to permit the simultaneous estimation of the states and the unknown inputs. For a class of nonlinear systems with unknown inputs, the work of [9] has proposed a high gain observer to estimate the states and unknown inputs. In [10] , a robust unknown input observer for linear and nonlinear systems was proposed in LMI formulation. An unknown input observer for a class of nonlinear uncertain system, especially consider the linear uncertainties on output matrix, was proposed by [11] and the observer design problem was solved via strong conditions. Most of the observers above were only used to deal with the system, which measured output is a linear combination of the system state, but for the nonlinear case, there are only a few results [4] [5] [7] [9] to deal with the measurement disturbances. Specially, in [9] , PI observer design was discussed for a system with constant measurement disturbances. An interesting reformulation of PI observer was given by [5] , but it is only valid for attenuating a certain bounded noise in a single output linear uncertain system. A proportional multiple integral observer for descriptor system was proposed by [7] , which allows us to decouple or attenuate measurement output disturbances. However, to the best of our knowledge, for the measured output with uncertain nonlinearities on the system states, there are no results.
Therefore, in consideration of the recent progress in the integral control domain, the development of integral observer is so far behind. This point is easy to be seen in the literatures [12] - [18] . General integral control designs based on linear system theory, sliding mode technique and feedback linearization technique were presented by [12] - [14] , respectively. In references [15] and [16] , general concave and convex integral control along with the bounded integral control actions were proposed, respectively. The method to construct general bounded integral control was presented by [17] . The generalization of integrator and integral control action appeared in [18] . All these nonlinear integral control strategies above stimulate us to develop the nonlinear integral observer and use it to deal with the system with uncertain nonlinearities that appear on both the system dynamics and measured outputs.
Motivated by the cognitions above, this paper proposes a conventional P_NI observer and two kinds of added-order P_NI observers along with their design method, respectively. The main contributions are as follows: 1) A kind of fire new nonlinear integrator and integral action is proposed; 2) The gap that there is not nonlinear integral observer is filled by presenting three kinds of nonlinear integral observers; 3) For the system with uncertain nonlinearities that appear on both the system dynamics and measured outputs, two solutions, that is, mixed and pure added-order P_NI observers, are provided; 4) By linear system theory and Lyapunov method, the conditions on the observer gains to ensure the estimated error to be ultimate boundness, which shrinks to zero as the states and control inputs converge to the equilibrium point, are provided. This means that if the observed system is asymptotically stable, the estimated error dynamics is asymptotically stable, too. Moreover, the highlight point of this paper is that the design of nonlinear integral observer is achieved by linear system theory.
Throughout this paper, we use the notation 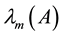 and
and 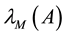 to indicate the smallest and largest eigen-
to indicate the smallest and largest eigen-
values, respectively, of a symmetric positive define bounded matrix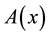 , for any
, for any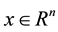 . The norm of vector
. The norm of vector
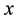 is defined as
is defined as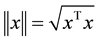 , and that of matrix
, and that of matrix 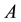 is defined as the corresponding induced norm
is defined as the corresponding induced norm
 .
.
The remainder of the paper is organized as follows: Section 2 describes the system under consideration, assumption and definition. Section 3 addresses the design of nonlinear integral observers. Simulations are provided in Section 4. Conclusions are presented in Section 5.
2. Problem Formulation
Consider the following observable nonlinear system,
 (1)
(1)
where 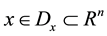 is the state,
is the state,  is the control input,
is the control input, 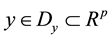 is the measured output,
is the measured output, 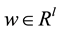 is a vector of unknown constant parameters and disturbances,
is a vector of unknown constant parameters and disturbances, 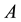 and
and 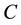 are all constant matrices.
are all constant matrices.
For convenience, we state all definitions, assumptions and theorems for the case when the equilibrium point is at the origin of , that is,
, that is,![]() .
.
Assumption 1: No loss of generality, suppose that the function ![]() and
and ![]() satisfy the equation,
satisfy the equation,
![]() (2)
(2)
where ![]() is the steady-state control that is needed to maintain equilibrium at the origin of
is the steady-state control that is needed to maintain equilibrium at the origin of![]() .
.
For the purpose of this paper, it is convenient to introduce the following definition.
Definition 1: ![]() with
with![]() ,
, ![]() , and
, and ![]() denotes the set of all continuous differen-
denotes the set of all continuous differen-
tial increasing functions [17] , ![]() such that
such that![]() ,
,
![]()
where ![]() stands for the absolute value.
stands for the absolute value.
Figure 1 depicts the example curves for one component of the function belonging to the function set![]() . For instance, for all
. For instance, for all![]() , the functions,
, the functions, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (
(![]() ,
,![]() ),
), ![]() , and so on, all belong to function set
, and so on, all belong to function set![]() .
.
3. Observer Design
This section proposes three kinds of nonlinear integral observers, respectively. First, a conventional P_NI observer is proposed to deal with the system without uncertainties in measured output; Second, a mixed added- order P_NI observer was developed for the system with the uncertain nonlinearities that appear on both the system dynamics and measured outputs; Finally, a pure added-order P_NI observer is provided to simplify the design of mixed added-order P_NI observer.
3.1. Conventional P_NI Observer
For the system (1), a conventional P_NI observer can be designed as follows,
![]() (3)
(3)
where ![]() is the estimated state;
is the estimated state; ![]() is the prescient constant parameters and/or disturbances;
is the prescient constant parameters and/or disturbances; ![]() is the esti-
is the esti-
mated output; ![]() belongs to the function set
belongs to the function set![]() ;
;![]() ;
; ![]() and
and ![]() are all
are all
gain matrices; ![]() and
and ![]() are the nominal models of
are the nominal models of ![]() and
and![]() , respectively. Here,
, respectively. Here, ![]() needs to satisfy
needs to satisfy![]() .
.
Thus, the error dynamics can be obtained by subtracting (3) from (1),
![]() (4)
(4)
where ![]() is the estimation state error,
is the estimation state error,
![]() ,
,
![]()
and ![]() is chosen to be nonsingular and large enough such that the equation,
is chosen to be nonsingular and large enough such that the equation,
![]() (5)
(5)
holds as![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() of the error dynamics (4).
of the error dynamics (4).
![]()
Figure 1. Example curves for one component of the function belonging to the function set![]() .
.
Therefore, we ensure that there is a unique solution![]() , and then
, and then ![]() is the unique equilibrium point of the system (4) in the domain of interest. At the equilibrium point,
is the unique equilibrium point of the system (4) in the domain of interest. At the equilibrium point, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and![]() , irrespective of the value of
, irrespective of the value of![]() .
.
Assumption 2: By Assumption 1 and the definitions of ![]() and
and![]() , it is reasonable to suppose them to satisfy,
, it is reasonable to suppose them to satisfy,
![]() (6)
(6)
![]() (7)
(7)
where![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() are all positive constants.
are all positive constants.
Now, the design task is to provide the conditions on the gains ![]() and
and ![]() such that
such that![]() . In the absence of
. In the absence of ![]() and
and![]() , the asymptotic stability of the error dynamics (4) can be achieved by designing the matrix
, the asymptotic stability of the error dynamics (4) can be achieved by designing the matrix
![]()
is Hurwitz.
By linear system theory, a quadratic Lyapunov function ![]() can be obtained. Where
can be obtained. Where ![]() is the
is the
solution of Lyapunov equation ![]() and
and![]() .
.
We use ![]() as a Lyapunov function candidate, and then the time derivative of
as a Lyapunov function candidate, and then the time derivative of ![]() along the trajectories of the error dynamics (4) is,
along the trajectories of the error dynamics (4) is,
![]() (8)
(8)
where![]() .
.
Now, using (2), (6) and (7), we have,
![]() (9)
(9)
Substituting (4) into (8), using the inequality (9), Lyapunov equation ![]() with
with![]() , and
, and
![]() , obtain,
, obtain,
![]() (10)
(10)
where![]() ,
, ![]() and
and![]() .
.
The first term in the right-hand side of the inequality (10) is negative define when,
![]() (11)
(11)
Furthermore, if the following inequality,
![]() (12)
(12)
holds, it can be verified,
![]() (13)
(13)
where![]() . Thus, the trajectory of the error dynamics (4) reaches the set
. Thus, the trajectory of the error dynamics (4) reaches the set
![]()
in finite time. The above argument shows that the error dynamics (4) is ultimate boundness with an ultimate
bound that decreases as ![]() and
and ![]() reduce, that is,
reduce, that is, ![]() as
as ![]() and
and![]() . In fact,
. In fact,
![]() means
means ![]() and
and![]() . This demonstrates that if the nonlinear system (1) is asymptotically stable, and then the error dynamics (4) is asymptotically stable, too. Moreover, a method for estimating the error boundness is provided here. This established the following theorem.
. This demonstrates that if the nonlinear system (1) is asymptotically stable, and then the error dynamics (4) is asymptotically stable, too. Moreover, a method for estimating the error boundness is provided here. This established the following theorem.
Theorem 1: Under Assumption 1 and 2, if there exist the gain matrices ![]() and
and ![]() such that the following inequality,
such that the following inequality,
![]() (14)
(14)
and the inequality (11) hold, and then the error dynamics (4) is ultimate boundness with an ultimate bound that decreases as ![]() and
and ![]() reduce, that is,
reduce, that is, ![]() and
and ![]() as
as ![]() and
and![]() .
.
Discussion 1: From the error dynamics (4), it is obvious that the observer (3) is only effective for the system
with![]() , that is, by increasing gain
, that is, by increasing gain![]() , the uncertain nonlinear action
, the uncertain nonlinear action ![]() can be effe-
can be effe-
ctively attenuated. However, when![]() , it results in a dilemma, that is, as follows: 1) By increasing the only unrestricted gain matrix
, it results in a dilemma, that is, as follows: 1) By increasing the only unrestricted gain matrix![]() , the stability of the error dynamics (4) could not be ensured though it can increase the stability margin; 2) The uncertain nonlinear term
, the stability of the error dynamics (4) could not be ensured though it can increase the stability margin; 2) The uncertain nonlinear term ![]() in the error dynamics (4), will be amplified unavoidably if the gain
in the error dynamics (4), will be amplified unavoidably if the gain ![]() is high. Thus, the design of the conventional P_NI observer is not a trivial task because the only way to solve this dilemma is that the precision of model
is high. Thus, the design of the conventional P_NI observer is not a trivial task because the only way to solve this dilemma is that the precision of model ![]() has to be improved. This leads to another worse trouble. Therefore, a new observer is proposed to solve this trouble in the next subsection.
has to be improved. This leads to another worse trouble. Therefore, a new observer is proposed to solve this trouble in the next subsection.
3.2. Mixed Added-Order P_ NI Observer
For making up the shortage of conventional P_NI observer and designing an added-order P_NI observer, the system (1) needs to be added order, which is motivated by the design idea presented by [5] , as follows,
![]() (15)
(15)
By the augmented system (15), a mixed added-order P_NI observer can be given as,
![]() (16)
(16)
where![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() are all the gain matrices
are all the gain matrices
and the other symbols are the same as these defined in (3).
By the same way as Subsection 3.1, the error dynamics can be obtained by subtracting (16) from (15),
![]() (17)
(17)
where![]() .
.
Now, the design task is to provide the conditions on the gain matrices![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]()
such that ![]() and
and![]() . In the absence of the uncertain terms
. In the absence of the uncertain terms ![]() and
and
![]() , the asymptotic stability of the error dynamics (17) can be achieved by designing the matrix,
, the asymptotic stability of the error dynamics (17) can be achieved by designing the matrix,
![]()
is Hurwitz.
Now, using (2), (6) and (7), we have,
![]() (18)
(18)
where
![]()
By the same way as Subsection 3.1, we can obtain a quadratic Lyapunov function![]() , and
, and
then using (18), if the following inequality,
![]() (19)
(19)
holds, we have,
![]() (20)
(20)
and then the time derivative of ![]() along the trajectories of the error dynamics (17) satisfies,
along the trajectories of the error dynamics (17) satisfies,
![]() (21)
(21)
where![]() ,
, ![]() ,
,
![]() , ,
, ,
![]()
and ![]() is the solution of
is the solution of![]() .
.
Thus, the trajectory of the error dynamics (17) reaches the set,
![]()
in finite time. As shown in Subsection 3.1, the following theorem can be established.
Theorem 2: Under Assumption 1 and 2, if there exist the gain matrices![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() such that the following inequality,
such that the following inequality,
![]() (22)
(22)
and the inequality (19) hold, and then the error dynamics (17) is ultimate boundness with an ultimate bound that
decreases as ![]() and
and ![]() reduce, that is,
reduce, that is, ![]() ,
, ![]() and
and ![]() as
as ![]() and
and![]() .
.
Remark 1: It is obvious that the order of the system (15) and observer (16) are all added. This is why our observer is called the added-order observer. In addition, the observer (16) is designed by using the estimated errors ![]() and
and![]() , that is the reason why the observer (16) is called mixed added-order observer.
, that is the reason why the observer (16) is called mixed added-order observer.
Discussion 2: From the error dynamics (17), it is easy to see that: 1) By increasing ![]() and
and![]() , we can attenuate the actions
, we can attenuate the actions ![]() and
and ![]() on
on ![]() and
and![]() , respectively; 2) By increasing
, respectively; 2) By increasing![]() , one is that the action
, one is that the action ![]() on
on ![]() can be limited, another is that it counteracts the actions
can be limited, another is that it counteracts the actions ![]() on
on ![]() and
and ![]() on
on![]() , too; 3) Although
, too; 3) Although ![]() and
and ![]() have all the actions to stabilize the error dynamics, they introduce
have all the actions to stabilize the error dynamics, they introduce ![]() into the dynamics of
into the dynamics of ![]() and
and![]() , too. Thus, if
, too. Thus, if ![]() and
and ![]() are moderate,
are moderate, ![]() is large enough, and
is large enough, and ![]() and
and ![]() are chosen such that
are chosen such that ![]() and
and![]() , then we can effectively attenuate the nonlinear actions
, then we can effectively attenuate the nonlinear actions ![]() and
and ![]() on the error dynamics. Consequently, we can ensure that the error is bounded.
on the error dynamics. Consequently, we can ensure that the error is bounded.
Obviously, the design method above is too complicated such that some sort of compromise is needed in practice. Therefore, a simplified observer will be proposed in the next subsection.
3.3. Pure Added-order P_ NI Observer
Based on Discussion 2, it is obvious that only the actions of ![]() and
and ![]() have two kinds of complexion that is positive and negative. Therefore, if we remove them from the observer (16), a pure added-order nonlinear integral observer can be obtained as follows,
have two kinds of complexion that is positive and negative. Therefore, if we remove them from the observer (16), a pure added-order nonlinear integral observer can be obtained as follows,
![]() (23)
(23)
where![]() ,
, ![]() ,
, ![]() and
and ![]() are all the gain matrices and the other symbols
are all the gain matrices and the other symbols
are the same as these defined in (3).
By the same way as Subsection 3.2, the error dynamics can be obtained by subtracting (23) from (15),
![]() (24)
(24)
and then by letting ![]() in Subsection 3.2, a simpler theorem can be established.
in Subsection 3.2, a simpler theorem can be established.
Theorem 3: Under Assumption 1 and 2, if there exist the gain matrices![]() ,
, ![]() and
and ![]() such that the following inequalities,
such that the following inequalities,
![]() (25)
(25)
![]() (26)
(26)
hold, and then the error dynamics (24) is ultimate boundness with an ultimate bound that decreases as ![]() and
and
![]() reduce, that is,
reduce, that is, ![]() ,
, ![]() and
and ![]() as
as ![]() and
and![]() .
.
Remark 2: It is easy to see that the observer (23) is designed only by the estimated error![]() , that is the reason why the observer (23) is called pure added-order P_NI observer.
, that is the reason why the observer (23) is called pure added-order P_NI observer.
Discussion 3: From the error dynamics (24) and demonstration above, it is obvious that: 1)![]() ,
, ![]() and
and ![]() are all independent gain matrices; 2) The matrix
are all independent gain matrices; 2) The matrix ![]() and the bound of the nonlinear actions (18) can all be
and the bound of the nonlinear actions (18) can all be
simplified; 3) By increasing ![]() and
and![]() , we can attenuate the actions
, we can attenuate the actions ![]() and
and ![]() on
on ![]()
and![]() , respectively. Thus, the observer (23) not only can effectively deal with the uncertain nonlinear ac-
, respectively. Thus, the observer (23) not only can effectively deal with the uncertain nonlinear ac-
tions on system (1) but also the stability of the error dynamics is easier to be achieved. Moreover, since the integral action can attenuate measurement noise, the observer (23) can be suitable for handling measurement noise, too.
Discussion 4: Although the works of [5] [7] and the observers (15) and (23) all use the same reformulation proposed by [5] , their main differences are as follows: 1) The integral action and integrator, here they are all nonlinear, but they are all linear in [5] [7] ; 2) The observed system, here it is used to deal with the uncertain nonlinear system, however, it is used to deal with the uncertain linear system and descriptor system in [5] [7] , respectively; 3) The twice integrals of measured output and estimated one, they are used to decouple or attenuate measurement output disturbances in [7] , but this paper uses it to counteract the unknown constant uncertainties produced by the model errors, prescient constant parameters and unknown steady-state control input.
Discussion 5: Compared with the integrators and integral actions proposed by [2] - [18] , the main differences are that: 1) The integrator and integral action: here are all nonlinear; however, they are all linear in [2] - [11] , except for the reference [11] , where the diffeomorphism is used as the integrator; 2) The indispensable components to construct the integrator: here are the linear form on the estimated errors; however, they are taken as the partial derivative of Lyapunov function in [14] - [16] and a general function on all the system states in [17] [18] , respect-
tively; 3) The integral actions: here not only include bounded integral actions, such as![]() , but al-
, but al-
so contains the unbounded one; however, they are all bounded in [15] - [17] ; 4) The correlations between the integrator and integral action: here they are closely related; however, they are independent of each other in [2] - [11] and [18] . Therefore, the nonlinear integrator and integral action proposed here are fire new.
Remark 3: From the stability analysis of Subsections 3.1 - 3.3, it is obvious that: Just the integrator is taken
as the product of estimated error and reciprocal of derivative![]() , the time derivative of integral action
, the time derivative of integral action
can be transformed into the linear form on the estimated error. Just with this ingenious mathematical transformation [15] , we can use linear system theory to analyze the stability of the error dynamics with the nonlinear integral action and integrator. As a result, this is a highlight point of this paper.
4. Simulations
Consider the pendulum system [19] described by,
![]()
where![]() ,
, ![]() ,
, ![]() ,
, ![]() is the angle subtended by the rod and the vertical axis,
is the angle subtended by the rod and the vertical axis,
and ![]() is the torque applied to the pendulum. View
is the torque applied to the pendulum. View ![]() as the control input and suppose we want to regulate
as the control input and suppose we want to regulate
![]() to
to![]() . For the purpose of this paper, we add an uncertain nonlinear action
. For the purpose of this paper, we add an uncertain nonlinear action ![]() on the
on the
measured output![]() , and then taking
, and then taking![]() ,
, ![]() and
and![]() , the pendulum system with the extra non-
, the pendulum system with the extra non-
linear action can be written as,
![]()
By the design method proposed here, the augmented system can be given as,
![]()
and then, the pure added-order P_NI observer can be given as,
![]()
By the design method proposed here, we can take![]() ,
, ![]() ,
, ![]() and
and ![]() such that the matrix
such that the matrix
![]()
is Hurwitz.
Therefore, the control input can be taken as,
![]()
For demonstrating the performance of the pure added-order observer, the simulations are implemented under normal and perturbed parameter cases, respectively.
Normal case: The initial states are![]() ,
, ![]() ,
, ![]() and
and![]() ; the system parameters are
; the system parameters are ![]() and
and![]() .
.
Perturbed case: The initial states are![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() ; the system parameters are
; the system parameters are![]() ,
, ![]() and
and![]() , corresponding to doubling of the mass.
, corresponding to doubling of the mass.
Figure 2 and Figure 3 showed the simulation results under the normal (solid line) and perturbed (dashed line) cases. As shown on Figure 2, the good control performance is still preserved, even under the perturbed case. This demonstrated that the observer (23) can be applied to the observer-based control. Figure 3 clearly shows that the estimated velocity error quickly shrinks to zero as the position tends to the equilibrium point. This not
![]()
Figure 2. System output under the normal (solid line) and per- turbed (dashed line) cases.
![]()
Figure 3. Velocity error under the normal (solid line) and per- turbed (dashed line) cases.
only verified the justification of Theorem 3 but also shows that the observer (23) has strong robustness and can effectively deal with the uncertain nonlinearities on both the system dynamics and measured outputs.
5. Conclusion
This paper proposed a conventional P_NI observer and two kinds of added-order P_NI observers along with their design method. The main contributions are as follows: 1) A kind of fire new nonlinear integrator and integral action is proposed; 2) The gap that there is not nonlinear integral observer is filled by presenting three kinds of nonlinear integral observers; 3) For the system with uncertain nonlinearities that appear on both the system dynamics and measured outputs, two solutions, that is, mixed and pure added-order P_NI observers, are provided; 4) The conditions on the observer gains to ensure the estimated error to be ultimate boundness, which shrinks to zero as the states and control inputs converge to the equilibrium point, are provided. This means that if the observed system is asymptotically stable, the estimated error dynamics is asymptotically stable, too. In addition, the highlight point of this paper is that the design of nonlinear integral observer was achieved by linear system theory.