Hall Effects on Unsteady MHD Three Dimensional Flow through a Porous Medium in a Rotating Parallel Plate Channel with Effect of Inclined Magnetic Field ()
1. Introduction
The rotating flow between parallel plates is a classical problem that has important applications in magneto hydro dynamic (MHD) power generators and pumps, accelerators, aerodynamic heating, electrostatic precipitation polymer technology, petroleum industry, purification of crude oil and fluid droplets, sprays, designing cooling systems with liquid metal, centrifugal separation of matter from fluid and flow meters. The flows of fluids through porous medium are very important particularly in the fields of agricultural engineering for irrigation processes; in petroleum technology to study petroleum transport; in chemical engineering for filtration and purification processes. A series of investigations have been made by (Raptis et al., 1981 [1] ; Raptis et al., 1981 [2] , Raptis et al., 1982 [3] ) into the steady of two-dimensional flow past a vertical wall for constant permeability of the porous medium. (Singh and Verma, 1995 [4] ) analyzed an oscillatory three-dimensional flow through a porous medium when the permeability varied in space periodically. (Singh et al., 2000 [5] ) investigated further a three-dimensional fluctuating flow and heat transfer through a porous medium when the permeability varied both in time and space. Further the flow of electrically conducting fluids in channels and pipes under the effect of transverse magnetic field occur in magnetohydrodynamic (MHD) generators, accelerators, pumps and flow meters. In view of these and many other important applications of these flows a number of scholars have shown their interest. Notable amongst them are (Shercliff, 1965 [6] ; Ferraro and Plumpton, 1966 [7] ; Crammer and Pai 1973, [8] ). (Yen and Chang, 1964 [9] ) studied the effects of wall electrical conductance on the MHD Couette flow. A magnetohydrodynamic (MHD) flow in a duct has also been studied by (Chang and Lundgren, 1961 [10] ). (Attia and Kotb, 1996 [11] ) investigated the two dimensional MHD flow between two porous, parallel, infinite, insulated, horizontal plates and the heat transfer through it when the lower plate was kept stationary and the upper plate was moving with uniform velocity. Very recently (Singh and Mathew, 2008 [12] ) studied the injection/suction effect on a hydromagnetic oscillatory flow in a horizontal porous channel in a rotating system. The Hall current effect on the velocity and temperature fields of an unsteady Hartmann number has also been studied by (Attia, 2006 [13] ). (Singh and Sharma, 2001 [14] ) studied a three-dimensional Couette flow with transpiration cooling in the presence of stationary magnetic field applied perpendicular to the planes of the insulated plates. Another aspect of the above three-dimensional Couette flow when the magnetic field is fixed with the moving plate has also been investigated by (Singh, 2004 [15] ). There are various other industrial applications of flows of electrically conducting fluids in the fields of geothermal systems, nuclear reactors, filtration, etc. where the conducting fluid flows through a porous medium which also rotates about an axis. In view of the importance of rotating flows a number of studies have appeared in the literature. (Mazumder, 1991 [16] ) studied an oscillatory Ekman boundary layer flow bounded by two horizontal plates one of which is oscillating and the other is at rest. (Ganapathy, 1994 [17] ) presented an alternative solution to the above problem. (Mazumder et al., 1976 [18] ) analyzed the Hall effects on combined free and forced convection hydromagnetic flow through a channel. (Singh, 2000 [19] ) studied the effects of transversely applied uniform magnetic field on oscillatory flow between two parallel flat plates when the entire system rotates about an axis normal to the planes of the plates. Hartman and Lazarus (1937 [20] ) studied the influence of a transverse uniform magnetic field on the flow of a viscous incompressible electrically conducting fluid between two infinite parallel stationary and insulating plates. Then the problem was extended in numerous ways. The Hall current is important and it has a marked effect on the magnitude and direction of the current density and consequently on the magnetic force. The unsteady hydro magnetic viscous flow through a nonporous or porous medium has drawn attention in the recent years for possible applications in geophysical and cosmical fluid dynamics. Debnath et al. (1979 [21] ) have studied the effects of Hall current on unsteady hydro magnetic flow past a porous plate in a rotating fluid system and the structure of the steady and unsteady flow fields is investigated. Rao and Krishna (1981 [22] ) studied Hall effects on the non-torsionally generated unsteady hydro magnetic flow in semi-infinite expansion of an electrically conducting viscous rotating fluid. Krishna and Rao (1982 [23] ) discussed the Stokes and Eckmann problems in magneto hydro dynamics taking Hall effects into account. M. VeeraKrishna and S. V. Suneetha (2009 [24] ) discussed Hall effects on unsteady flow of incompressible viscous fluid between two rigid non-conducting rotating plates through porous medium under the influence of a uniform transverse magnetic field. S. V. Suneetha et al. (2010 [25] ) discussed Hall effects on unsteady rotating magneto hydro dynamic flow of an incompressible homogeneous second grade fluid through a porous half space. Recently Hall effects on an unsteady MHD flow of a viscous incompressible electrically conducting fluid in a horizontal porous channel with variable pressure gradient in a rotating system have been studied by Sanatan Das and Rabindranath Jana (2013 [26] ). In this paper, we make an initial value investigation of the unsteady flow of incompressible viscous fluid between two rigid non-conducting rotating parallel plates bounded by a porous medium taking hall current into account.
2. Formulation and Solution of the Problem
We consider the unsteady flow of an incompressible electrically conducting viscous fluid bounded by porous medium with two non-conducting rotating parallel plates. A uniform transverse magnetic field is applied to z-axis. In the presence of strong magnetic field a current is inclined in a direction normal to the both electric and magnetic field viz. Magnetic field of strength H0 inclined at angle of inclination 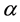 to the normal to the boundaries in the transverse xz-plane. The inclined magnetic field gives rise to a secondary flow transverse to the channel. The hydro magnetic flow is generated in a fluid system by non-torsional oscillations of the upper plate. The lower plate is at rest. The origin is taken on the lower plate and the x-axis parallel to the direction of the upper plate. Since the plates are infinite in extent, all the physical quantities except the pressure depend on z and t only. In the equation of motion along x-direction, the x-component current density―
to the normal to the boundaries in the transverse xz-plane. The inclined magnetic field gives rise to a secondary flow transverse to the channel. The hydro magnetic flow is generated in a fluid system by non-torsional oscillations of the upper plate. The lower plate is at rest. The origin is taken on the lower plate and the x-axis parallel to the direction of the upper plate. Since the plates are infinite in extent, all the physical quantities except the pressure depend on z and t only. In the equation of motion along x-direction, the x-component current density―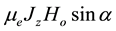 and the z- component current density
and the z- component current density . We choose a Cartesian system 0 (x, y, z) such that the boundary walls are at z = 0 and z = l. The flow through porous medium governed by the Brinkman equations. The unsteady hydro magnetic equations governing flow through porous medium under the influence of a transverse magnetic field with reference to a rotating frame are
. We choose a Cartesian system 0 (x, y, z) such that the boundary walls are at z = 0 and z = l. The flow through porous medium governed by the Brinkman equations. The unsteady hydro magnetic equations governing flow through porous medium under the influence of a transverse magnetic field with reference to a rotating frame are
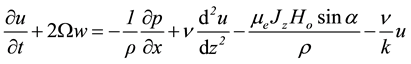 (1)
(1)
 (2)
(2)
where, (u, w) is the velocity components along O (x, z) directions respectively. 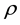 is the density of the fluid,
is the density of the fluid,  is the magnetic permeability,
is the magnetic permeability,  is the coefficient of kinematic viscosity, k is the permeability of the medium,
is the coefficient of kinematic viscosity, k is the permeability of the medium, 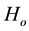 is the applied magnetic field. When the strength of the magnetic field is very large, the generalized Ohm’s law is modified to include the Hall current, so that
is the applied magnetic field. When the strength of the magnetic field is very large, the generalized Ohm’s law is modified to include the Hall current, so that
 (3)
(3)
where, q is the velocity vector, H is the magnetic field intensity vector, E is the electric field, J is the current density vector, 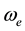 is the cyclotron frequency,
is the cyclotron frequency,  is the electron collision time,
is the electron collision time, 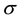 is the fluid conductivity and,
is the fluid conductivity and,  is the magnetic permeability. In Equation (3) the electron pressure gradient, the ion-slip and thermo- electric effects are neglected. We also assume that the electric field E = 0 under assumptions reduces to
is the magnetic permeability. In Equation (3) the electron pressure gradient, the ion-slip and thermo- electric effects are neglected. We also assume that the electric field E = 0 under assumptions reduces to
 (4)
(4)
 (5)
(5)
where ![]() is the Hall parameter.
is the Hall parameter.
On solving Equations (4) and (5) we obtain
![]() (6)
(6)
![]() (7)
(7)
Using the Equations (6) and (7), the equations of the motion with reference to rotating frame are given by
![]() (8)
(8)
![]() (9)
(9)
By combining the Equations (8) and (9), we get.
Let ![]()
![]() (10)
(10)
The boundary and initial conditions are
![]() (11)
(11)
![]() (12)
(12)
We introduce the following non dimensional variables are
![]()
Using non-dimensional variables, the governing equations are (dropping asterisks)
![]() (13)
(13)
where,
![]() is the Hartmann number;
is the Hartmann number;
![]() is the rotation parameter;
is the rotation parameter;
![]() is inverse Darcy parameter and;
is inverse Darcy parameter and;
![]() is the Hall parameter.
is the Hall parameter.
We choose ![]() is the prescribed of pressure gradient, then the Equation (13) reduces to
is the prescribed of pressure gradient, then the Equation (13) reduces to
![]() (14)
(14)
Corresponding initial and boundary conditions are
![]() (15)
(15)
![]() (16)
(16)
Taking Laplace transform of Equation (14) using initial condition (15) the governing equations in terms of the transformed variable reduces to
![]() (17)
(17)
The relevant transformed boundary conditions are
![]() (18)
(18)
![]() (19)
(19)
Solving the Equation (17) and making use of the boundary conditions (18) and (19), we obtain
![]() (20)
(20)
where
![]() ,
,
![]()
![]()
Taking inverse Laplace transform to the Equation (20), we obtain
![]() (21)
(21)
![]()
The shear stresses on the upper plate and the lower plate are given by
![]() (22)
(22)
3. Results and Discussion
The flow is governed by the non-dimensional parameters M the Hartman number, D−1 the inverse Darcy parameter, K is the rotation parameter and m is the Hall parameter. The velocity field in the porous region is evaluated analytically its behaviour with reference to variations in the governing parameters has been computationally analyzed. The profiles for u and w have been plotted in the entire flow field in the porous medium. The solution for the velocity consists of three kinds of terms 1) steady state, 2) the quasi-steady state terms associated with non-torsional oscillations in the boundary, 3) the transient term involving exponentially varying time dependence. From the expression (21), it follows that the transient component in the velocity in the fluid region
decays in dimensionless time![]() . When the transient terms decay the steady oscillatory
. When the transient terms decay the steady oscillatory
solution in the fluid region is given by
![]() (23)
(23)
![]() (24)
(24)
We now discuss the quasi steady solution for the velocity for different sets of governing parameters namely viz. M the Hartman number and D−1 the inverse Darcy parameter, K the rotation parameter, m is the Hall parameter, P0 & P1 the non dimensional pressure gradients, the frequency oscillations ω, a and b the constants related to non torsional oscillations of the boundary, for computational analysis purpose we are fixing the axial pressure gradient as well as a and b, and![]() ,
, ![]() ,
, ![]() ,
,![]() . Figures 1-8 corresponding to the velocity components u and w along the prescribed pressure gradient for different sets of governing parameters when the upper boundary plate executes non-torsional oscillations. The magnitude of the velocity u and w increases for the sets of values 0.1 ≤ z ≤ 0.3 as well as which reduces for all values of z with increase in the intensity of the magnetic field (Figure 1 and Figure 5). The resultant velocity q decreases with increasing the Hartmann number M. The magnitude of the velocity u decreases in the upper part of the fluid region 0.1 ≤ z ≤ 0.2 while it experiences enhancement lower part 0.3 ≤ z ≤ 0.9 with increasing the inverse Darcy parameter D−1 (Figure 2). The magnitude of the velocity w increases in the upper part of the fluid region 0.1 ≤ z ≤ 0.3, while it reduces in lower part 0.4 ≤ z ≤ 0.9 with increasing the inverse Darcy parameter D−1 (Figure 6). The resultant velocity q reduces with increasing the inverse Darcy parameter D−1. The magnitude of velocity u decreases in the upper part of the fluid region while it experiences enhancement lower part 0.3 ≤ z ≤ 0.9 and also the magnitude of velocity w increases throughout the fluid region (Figure 3 and Figure 7). However the resultant velocity q enhances with increasing the Hall parameter m. Finally we notice that, from (Figure 4 and Figure 8) the magnitude of the velocity component enhances for 0.1 ≤ z ≤ 0.3 and z = 0.7, and reduces within the region 0.4 ≤ z ≤ 0.6 and 0.8 ≤ z ≤ 0.9 with increase in rotation parameter K. while the velocity component w enhances for 0.3 ≤ z ≤ 0.4 and z = 0.9, and reduces for 0.1 ≤ z ≤ 0.2, with increase in rotation parameter K.
. Figures 1-8 corresponding to the velocity components u and w along the prescribed pressure gradient for different sets of governing parameters when the upper boundary plate executes non-torsional oscillations. The magnitude of the velocity u and w increases for the sets of values 0.1 ≤ z ≤ 0.3 as well as which reduces for all values of z with increase in the intensity of the magnetic field (Figure 1 and Figure 5). The resultant velocity q decreases with increasing the Hartmann number M. The magnitude of the velocity u decreases in the upper part of the fluid region 0.1 ≤ z ≤ 0.2 while it experiences enhancement lower part 0.3 ≤ z ≤ 0.9 with increasing the inverse Darcy parameter D−1 (Figure 2). The magnitude of the velocity w increases in the upper part of the fluid region 0.1 ≤ z ≤ 0.3, while it reduces in lower part 0.4 ≤ z ≤ 0.9 with increasing the inverse Darcy parameter D−1 (Figure 6). The resultant velocity q reduces with increasing the inverse Darcy parameter D−1. The magnitude of velocity u decreases in the upper part of the fluid region while it experiences enhancement lower part 0.3 ≤ z ≤ 0.9 and also the magnitude of velocity w increases throughout the fluid region (Figure 3 and Figure 7). However the resultant velocity q enhances with increasing the Hall parameter m. Finally we notice that, from (Figure 4 and Figure 8) the magnitude of the velocity component enhances for 0.1 ≤ z ≤ 0.3 and z = 0.7, and reduces within the region 0.4 ≤ z ≤ 0.6 and 0.8 ≤ z ≤ 0.9 with increase in rotation parameter K. while the velocity component w enhances for 0.3 ≤ z ≤ 0.4 and z = 0.9, and reduces for 0.1 ≤ z ≤ 0.2, with increase in rotation parameter K.
The shear stresses ![]() and
and ![]() on the upper plate have been calculated for the different variations in the governing parameters and are tabulated in the Table 1, Table 2. On the upper plate we notice that the magnitudes of
on the upper plate have been calculated for the different variations in the governing parameters and are tabulated in the Table 1, Table 2. On the upper plate we notice that the magnitudes of ![]() enhances the inverse Darcy parameter D−1, the hall parameter m, rotation parameter K decreases with increase in the Hartmann number M (Table 1). The magnitude of
enhances the inverse Darcy parameter D−1, the hall parameter m, rotation parameter K decreases with increase in the Hartmann number M (Table 1). The magnitude of ![]() decreases with increase in the Hartmann number M, the inverse Darcy parameter D−1 rotation parameter K and the Hall parameter m fixing the other parameters (Table 2). The similar behaviour is observed on the lower plate (Table 3, Table 4). We also notice that the magnitude of the shear stresses on the lower plate is very small compare to its values of the upper plate.
decreases with increase in the Hartmann number M, the inverse Darcy parameter D−1 rotation parameter K and the Hall parameter m fixing the other parameters (Table 2). The similar behaviour is observed on the lower plate (Table 3, Table 4). We also notice that the magnitude of the shear stresses on the lower plate is very small compare to its values of the upper plate.
![]()
Figure 1. The velocity profile for u with M.
![]()
Figure 2. The velocity profile for u with D−1.
![]()
Figure 3. The velocity profile for u with m.
![]()
Figure 4. The velocity profile for u with K.
![]()
Figure 5. The velocity profile for w with M.
![]()
Figure 6. The velocity profile for w with D−1.
![]()
Figure 7. The velocity profile for w with m.
![]()
Figure 8. The velocity profile for w with K.
![]()
Table 1. The shear stress ![]() on the upper plate.
on the upper plate.
![]()
Table 2. The shear stress ![]() on the upper plate.
on the upper plate.
![]()
Table 3. The shear stress ![]() on the lower plate.
on the lower plate.
![]()
Table 4. The shear stress ![]() on the lower plate.
on the lower plate.
4. Conclusions
1) The resultant velocity q enhances with increasing hall parameter m and rotation parameter K, and decreases with increasing inverse Darcy parameter D−1 as well as the Hartmann number M.
2) On the upper plate the magnitude of ![]() enhances when increasing the hall parameter m; rotation parameter K and the inverse Darcy parameter D−1 decrease with increase in the Hartmann number M.
enhances when increasing the hall parameter m; rotation parameter K and the inverse Darcy parameter D−1 decrease with increase in the Hartmann number M.
3) On the upper plate the magnitude of shear stress enhances when increasing the hall parameter M; rotation parameter K and the inverse Darcy parameter D−1 decrease with increase in the Hartmann number M.
4) The similar behaviour is observed on the lower plate.
5) The magnitude of the shear stresses on the lower plate is very small than the values of the upper plate.