1. Introduction
Recent applications of iterated maps in numerical analysis have been found in literature, using and extending the techniques of dynamical systems to the study of numerical algorithms and number theory [1] -[3] . Application in technology and hardware devices are also frequent nowadays [4] - [7] .
We propose and study in this work two new methods for numerical root approximations, both of which based on iterated maps. In the following sections we present a detailed study of each map, their fixed points and stability, the occurrence of bifurcations and chaotic behavior.
Some common tools of nonlinear dynamics [8] [9] are used to the study of the orbits, i.e., the numerical time series obtained for each map are investigated. The numerical approximations 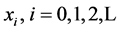 to solve the general equation
to solve the general equation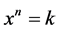 , where
, where 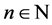 and
and 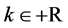 are obtained, but the validity of the results can be extended to
are obtained, but the validity of the results can be extended to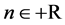 .
.
In Section 2 we present a new map proposed by one of us (C. C. Dias), named as First Dias Map (FDM), showing the existence of a fixed point for roots in the range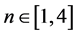 , and that this fixed point corresponds exactly to
, and that this fixed point corresponds exactly to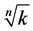 .
.
In Section 3, we generalize the FDM by adding a new parameter for studying the stability of its fixed point by defining a new class of maps called Weighted Average Map (WAM). For this class of maps, we investigate the dependence of the fixed point corresponding to the nth root of 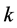 over the parameter space
over the parameter space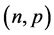 .
.
Finally, in Section 4, we measure and compare the Mean Convergence Time (MCT) for all the studied maps, for 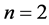 and
and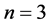 , varying
, varying 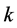 over an uniform grid of initial conditions and computing the average amount of iterations to converge to the root
over an uniform grid of initial conditions and computing the average amount of iterations to converge to the root 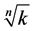 within the standard numerical double precision. An analytical model is proposed and used to confirm the numerical results of MCT with the analytical convergence time (ACT) for the WAM.
within the standard numerical double precision. An analytical model is proposed and used to confirm the numerical results of MCT with the analytical convergence time (ACT) for the WAM.
2. The First Dias Map (FDM)
The map which we will study now was created by Charles C. Dias to extract real roots of numbers numbers, by solving the equation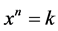 . The proposed map is one-dimensional and is defined as
. The proposed map is one-dimensional and is defined as
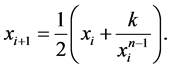 (1.1)
(1.1)
Comparing this with the Newton-Raphson Method (NRM) equation and Babylonian Method (BABM) [10] noticed that this statement is a mixture of both, and the FDM is an arithmetic average between the linear and nonlinear terms in Equation (1.1), and can be used to approximate the nth root of 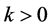 for
for![]() , as we shall see. Outside this interval of
, as we shall see. Outside this interval of![]() , this map presents chaotic dynamics through after entering a bifurcation cascade, whose roots having no longer relationship to the nth root of
, this map presents chaotic dynamics through after entering a bifurcation cascade, whose roots having no longer relationship to the nth root of![]() .
.
The base function that appears in the iterated map defined by Equation (1.1) can be derived dividing ![]() by
by![]() , for
, for![]() , leading to
, leading to
![]() (1.2)
(1.2)
and adding ![]() at both sides, and dividing it by 2, we recover functional form of Equation (1.1).
at both sides, and dividing it by 2, we recover functional form of Equation (1.1).
2.1. Geometrical Construction
To construct geometrically the FDM time series, the first step is to find the auxiliary equations of the lines ![]() (see Figure 1), writing their slopes
(see Figure 1), writing their slopes![]() . From this figure,
. From this figure, ![]() and
and![]() , and the slopes
, and the slopes
![]() (1.3)
(1.3)
that for ![]() are
are![]() .
.
Knowing that their linear coefficients are all![]() , then all the auxiliary lines pass through the point
, then all the auxiliary lines pass through the point![]() , we obtain the working lines
, we obtain the working lines ![]() and the auxiliary points
and the auxiliary points![]() , the intersections points of the working lines with the
, the intersections points of the working lines with the ![]() -axis, are
-axis, are
![]() (1.4)
(1.4)
and taking the arithmetic mean between the auxiliary points ![]() and the
and the ![]() points we recover the original FDM equation (Equation (1.1)).
points we recover the original FDM equation (Equation (1.1)).
Figure 2(a) shows the cobweb for the FDM time series for ![]() and
and![]() , and Table 1 (top) shows time series used in this figure. In this example, the convergence to the root is achieved after only five steps, considering the standard double precision, and is exactly the same time series of NRM for these parameters. Figure 2(b)
, and Table 1 (top) shows time series used in this figure. In this example, the convergence to the root is achieved after only five steps, considering the standard double precision, and is exactly the same time series of NRM for these parameters. Figure 2(b)
![]()
Figure 1. The FDM schematic geometrical path construction.
shows a numerical development of the FDM series for the parameters ![]() and
and![]() , based on the time series shown in Table 1 (bottom), where the convergence to the root occurs after 27 steps. Some intermediary time steps are omitted in this table.
, based on the time series shown in Table 1 (bottom), where the convergence to the root occurs after 27 steps. Some intermediary time steps are omitted in this table.
2.2. Fixed Point and Stability Analysis
Solving ![]() we find the FDM fixed point to be
we find the FDM fixed point to be![]() . Applying the stability criterion [11] , to the
. Applying the stability criterion [11] , to the
map function![]() , whose derivative is
, whose derivative is ![]() we obtain
we obtain![]() ,
,
and solving the last equation we have the range of parameter ![]() where the fixed point of the map is stable.
where the fixed point of the map is stable.
2.3. Numerical Results
The FDM time series have different dynamics depending on the parameters![]() , presenting a fixed point, periodicity or chaos, as occurs to the logistic map [12] .
, presenting a fixed point, periodicity or chaos, as occurs to the logistic map [12] .
To measure the rate of divergent orbits, i.e., the sensitive dependence on initial conditions, we can use is characteristic Lyapunov exponent![]() . From Figure 3(a) we see that, at
. From Figure 3(a) we see that, at![]() , FDM enters a bifurcation cascade, therefore its fixed point is no longer stable. In the white to gray regions the exponent is negative indicating that for this region of parameters the FDM not is chaotic, and at the black stripes the Lyapunov exponent
, FDM enters a bifurcation cascade, therefore its fixed point is no longer stable. In the white to gray regions the exponent is negative indicating that for this region of parameters the FDM not is chaotic, and at the black stripes the Lyapunov exponent
goes to zero signing the period bifurcations. The yellow to red regions indicate the a positive Lyapunov exponents, the signature of chaos.
The FDM bifurcation diagram, discarded a transient of 103 iterations and plotted the next 500 values of![]() , is depicted in Figure 3(b). The values of
, is depicted in Figure 3(b). The values of ![]() studied are uniformly distributed in a grid of 600 points in the interval
studied are uniformly distributed in a grid of 600 points in the interval![]() . Also plotted over the bifurcation diagram is the exact root
. Also plotted over the bifurcation diagram is the exact root![]() , the fixed point of the map, plotted in black.
, the fixed point of the map, plotted in black.
We also study numerically the FDM return diagrams for different values of the parameter![]() , for
, for ![]() and
and![]() , as seen in Figure 3(c) and Figure 3(d), respectively.
, as seen in Figure 3(c) and Figure 3(d), respectively.
3. The Weighted Average Map (WAM)
Instead of adding![]() , if a more general term
, if a more general term ![]() is added in Equation (1.2), we get a new map (WAM) that depends on parameters
is added in Equation (1.2), we get a new map (WAM) that depends on parameters![]() ,
, ![]() and
and![]() . The new parameter
. The new parameter ![]() is a positive real number and corresponds to the weight of the linear term of the map. This term is directly linked to the parameter
is a positive real number and corresponds to the weight of the linear term of the map. This term is directly linked to the parameter![]() , since for each value of
, since for each value of ![]() there is a minimum value of
there is a minimum value of ![]() for the fixed point to be stable, as we shall see.
for the fixed point to be stable, as we shall see.
Adding ![]() to both sides of Equation (1.2) we gain
to both sides of Equation (1.2) we gain
![]() (1.5)
(1.5)
and after collecting ![]() and dividing by
and dividing by ![]() it leads to the new map (WAM),
it leads to the new map (WAM),
![]() (1.6)
(1.6)
and solving its fixed point equation ![]() we obtain the expected value
we obtain the expected value![]() .
.
3.1. Fixed Point and Stability Analysis
Applying the stability criterion [11] , i.e., ![]() , to the map function
, to the map function ![]() whose derivative is
whose derivative is ![]() and solving this inequality we obtain
and solving this inequality we obtain ![]() to
to
guarantee fixed point stability, and Figure 4 shows the line corresponding to this condition, below which the fixed point is unstable. As ![]() is increased the value of
is increased the value of ![]() should also be increased to avoid the unstable region, where the time series do not converges to the fixed point.
should also be increased to avoid the unstable region, where the time series do not converges to the fixed point.
3.2. WAM Subclasses and Hierarchy
A special subclass of WAM is FDM, when![]() , so that the fixed point on the map according to Figure 4, is stable in the range
, so that the fixed point on the map according to Figure 4, is stable in the range ![]() for
for![]() , thus in accordance with the stability analysis the fixed point
, thus in accordance with the stability analysis the fixed point ![]() loses stability
loses stability
![]()
![]() (a) (b)
(a) (b)
Figure 4. For![]() , (a) the numerical results of WAM MCT (n, p) and (b) the analytical model for WAM ACT (n, p).
, (a) the numerical results of WAM MCT (n, p) and (b) the analytical model for WAM ACT (n, p).
at![]() . Other very important subclass is NRM, for
. Other very important subclass is NRM, for![]() , so that the weight
, so that the weight ![]() is chosen within the stable region.
is chosen within the stable region.
For NRM, the derivative of the mapping function at the fixed point is null, satisfying the stability criterion and resulting in the most efficient rate of convergence of the time series near the fixed point. When the starting point ![]() is chosen far away from the fixed point, we observe numerically that the initial rate of convergence is greater for FDM, in general. Finally, there is a third subclass of WAM, the Babylonian square root method (BABM), for
is chosen far away from the fixed point, we observe numerically that the initial rate of convergence is greater for FDM, in general. Finally, there is a third subclass of WAM, the Babylonian square root method (BABM), for ![]() and
and![]() , the oldest and perhaps the most efficient known method to solve the equation
, the oldest and perhaps the most efficient known method to solve the equation![]() . At this parameters, WAM reduces itself to BABM, therefore the same occurs with FDM and NRM. The hierarchy of WAM subclasses are shown in Figure 5.
. At this parameters, WAM reduces itself to BABM, therefore the same occurs with FDM and NRM. The hierarchy of WAM subclasses are shown in Figure 5.
From the definition of the Lyapunov characteristic exponent for a unidimensional map we conclude that the derivative of the mapping function at the fixed point ![]() defines the rate of convergence of its time series, discarded the transient. For WAM, it is easy to show that
defines the rate of convergence of its time series, discarded the transient. For WAM, it is easy to show that![]() , so that this derivative assumes the value
, so that this derivative assumes the value ![]() when
when ![]() (FDM) and is zero only if
(FDM) and is zero only if ![]() (NRM or BABM, if
(NRM or BABM, if![]() ). In Figure 3(c) we observe that
). In Figure 3(c) we observe that![]() , for
, for ![]() FDM reduces to NRM, and in Figure 3(d), we observe that
FDM reduces to NRM, and in Figure 3(d), we observe that![]() .
.
4. Mean Convergence Time (MCT)
This section reports the numerical results for the mean convergence time (MCT) for NRM, FDM and WAM, based on the average number of iterates to converge within different precisions![]() , from single
, from single ![]() to double
to double![]() . For this, we varied
. For this, we varied ![]() on a uniform grid with 103 points in the interval
on a uniform grid with 103 points in the interval![]() , varying the initial condition
, varying the initial condition ![]() on a second uniform grid with
on a second uniform grid with ![]() points, whose limits are given by a maximum relative difference of 25% around the exact value of the root of
points, whose limits are given by a maximum relative difference of 25% around the exact value of the root of ![]() at each point. Using this schema, the MCT is computed for cubic roots
at each point. Using this schema, the MCT is computed for cubic roots![]() , and for WAM we set
, and for WAM we set![]() . Figures 6(a)-(c) show the numerical results.
. Figures 6(a)-(c) show the numerical results.
In Figure 6(a) we see that the NRM MCT is close to 4, which means that after 4 iterations, on average, there has been convergence to the root. From this figure, we conclude that FDM is around 10 times slower than NRM, and WAM is around has twice the speed of FDM. In this test, the most efficient is NRM, with the lowest MCT.
Both NRM and FDM belong to the same WAM family, as discussed in Section 3, and the stability of the fixed point ![]() of WAM depends on the parameters
of WAM depends on the parameters ![]() and
and![]() . Changing the parameter
. Changing the parameter ![]() of WAM we get a new map subclass, for example, for
of WAM we get a new map subclass, for example, for ![]() have the FDM. From these fact, we tried to detect numerically the
have the FDM. From these fact, we tried to detect numerically the
![]()
Figure 5. Hierarchy of the WAM subclasses.
optimal value of the parameter![]() , to minimize the ACT over the whole WAM family. For this we used a FORTRAN program to measure extensively the WAM MCT varying parameters
, to minimize the ACT over the whole WAM family. For this we used a FORTRAN program to measure extensively the WAM MCT varying parameters ![]() on a uniform grid of
on a uniform grid of ![]() points, for a radicand
points, for a radicand![]() . The result for
. The result for ![]() is shown in Figure 4(a). The region in gray corresponds to unstable fixed point
is shown in Figure 4(a). The region in gray corresponds to unstable fixed point ![]() map WAM, as found in Section 1.3. The other colors seen in the graph are the regions of stability of the fixed point. For best visualization the MCT scale of this figure is truncated at a maximum value of 20, and higher values as inked light gray.
map WAM, as found in Section 1.3. The other colors seen in the graph are the regions of stability of the fixed point. For best visualization the MCT scale of this figure is truncated at a maximum value of 20, and higher values as inked light gray.
We can see in Figure 4(a) that, as we approach the line that corresponds to the weighting term, NRM shows the minimum MCT over this line and therefore the most efficient of all studied maps is the NRM.
Summarizing the key information about NRM, FDM and WAM, with the numerical results for the MCT within double precision for these maps, for the parameters ![]() and
and![]() , as shown in Table 2.
, as shown in Table 2.
Analytical Convergence Time Model
The Lyapunov characteristic exponent for a unidimensional map ![]() usually defined by
usually defined by
![]()
can be approximate by ![]() since the derivative of the mapping function at the fixed point
since the derivative of the mapping function at the fixed point ![]() defines the rate of convergence of its time series, after discarded the transient.
defines the rate of convergence of its time series, after discarded the transient.
For WAM, it is easy to show that![]() , so that this derivative assumes the value
, so that this derivative assumes the value ![]() when
when ![]() (FDM) and is zero only if
(FDM) and is zero only if ![]() (NRM or BABM, if
(NRM or BABM, if![]() ). In Figure 3(c) we observe that
). In Figure 3(c) we observe that![]() , for
, for ![]() FDM reduces to NRM, and in Figure 3(d),
FDM reduces to NRM, and in Figure 3(d),![]() .
.
Using the original Lyapunov’s idea, the characteristic exponent ![]() measures the average rate of convergence between two solutions separated by an initial distance
measures the average rate of convergence between two solutions separated by an initial distance![]() , that is the case of time series dominated by a fixed point. For this orbits, the distance after
, that is the case of time series dominated by a fixed point. For this orbits, the distance after ![]() iterates is
iterates is ![]() so that, if we assume that one orbit is initialized at
so that, if we assume that one orbit is initialized at ![]() and other at
and other at![]() , i.e., the initial distance is unitary between orbits, we can use last equation to measure the error found in the second orbit, the root to be approximated. Within the standard double precision, the maximum error is of order
, i.e., the initial distance is unitary between orbits, we can use last equation to measure the error found in the second orbit, the root to be approximated. Within the standard double precision, the maximum error is of order![]() , where
, where ![]() is the number of decimal significants, typically
is the number of decimal significants, typically ![]() places.
places.
Applying the natural logarithm to both sides of the above equation we have ![]() for the number of
for the number of
iterations needed to reduces the error in the second orbit to![]() . In the same manner we defined MCT, we define now the analytical convergence time (ACT), estimated by
. In the same manner we defined MCT, we define now the analytical convergence time (ACT), estimated by
![]() (1.7)
(1.7)
valid for any fixed point of a unidimensional map, where the approximated ![]() was used.
was used.
Applying this model to our more general map (WAM), we have
![]() (1.8)
(1.8)
of the parameters ![]() and
and![]() . To double precision this approximated model function is plotted in Figure 4(b), that is remarkably very close to the numerical version plotted in Figure 4(a). Both figures uses the same color palette and truncated maximum, for better comparisons.
. To double precision this approximated model function is plotted in Figure 4(b), that is remarkably very close to the numerical version plotted in Figure 4(a). Both figures uses the same color palette and truncated maximum, for better comparisons.
![]()
Table 2. MCT numerical results for NRM, FDM and WAM maps.
5. Conclusions
In the study of iterated maps to extract the real root of real numbers we have applied some common tools from nonlinear dynamics that allowed us to predict the fixed point of the studied maps associated with the nth root of![]() , and their stabilities could be analyzed in details.
, and their stabilities could be analyzed in details.
We conclude, through the geometric argument used to recover the original analytical form of FDM, that both NRM and FDM can be reduced to averages between two terms, one linear and other nonlinear. From this observation, we generalize the original FDM idea to a new family of maps on which we add a new parameter![]() , whose value defines the stability of the map, the WAM. We show that FDM and NRM belong to this family of maps, being FDM recover when
, whose value defines the stability of the map, the WAM. We show that FDM and NRM belong to this family of maps, being FDM recover when ![]() and NRM when
and NRM when![]() .
.
The mean convergence time (MCT) numerical results indicate that NRM is the most efficient subclass of the more general weighted average map (WAM) proposed in this work, as pointed out in Figure 4(a), over the line![]() . The analytical model for ACT is in complete agreement with the numerical results for WAM, the most general class of map studied. The model presented in Equation 1.7 is general, and can be adapted to any unidimensional map to study its fixed point attractor.
. The analytical model for ACT is in complete agreement with the numerical results for WAM, the most general class of map studied. The model presented in Equation 1.7 is general, and can be adapted to any unidimensional map to study its fixed point attractor.
The main results of this work are obtained for![]() , but their generalization is straightforward over the complex set
, but their generalization is straightforward over the complex set![]() .
.
Acknowledgements
This work was partially supported by the Brazilian agency Conselho Nacional de Desenvolvimento Cientfico e Tecnológico―CNPq and Universidade do Estado de Santa Catarina―UDESC.
NOTES
*Corresponding author.