Experimental and Numerical Investigation of a Rayleigh-Bénard Convection Affected by Coriolis Force

Claudia Zimmermann, Rodion Groll

Center of Applied Space Technology and Microgravity, University of Bremen, Bremen, Germany.

DOI: 10.4236/jfcmv.2014.24018                

Abstract

In this paper the influence of an impressed Coriolis force field on the configuration of a turbulent Rayleigh-Bénard convection problem is investigated in an experimental and numerical study. The main purpose of both studies lie on the analysis of a possible stabilising effect of a Coriolis acceleration on the turbulent unsteady structures inside the fluid. The relative Coriolis acceleration which is caused in the atmosphere by the earth rotation is realised in the experimental study by a uniform-rotational movement of the setup in a large-scale centrifuge under hyper-gravity. The same conditions as in the atmosphere in the beginning of a twister or hurricane should be realised in the experiment. The investigated Rayleigh numbers lie between 2.33 × 106 ≤ Ra ≤ 4.32 × 107.

Keywords

Rayleigh-Bénard Convection, Compressible Flow, Coriolis Force, PIV, Large-Eddy Simulation

1. Introduction

A Rayleigh-Bénard (RB) convection or Rayleigh-Bénard (RB) problem describes thermally driven flow against gravity between two horizontal, heated walls. The fluid is accelerated by local density differences and a resulting pressure gradient. Directly at the heated walls the temperature distribution is determinate by increasing temperature gradients, while convective mass exchange is dominant in the center region. Turbulent shear layers parallel to the direction of gravity develop between the walls. The first studies of a RB problem between horizontal, heated walls were performed by the French physicist Henri Claude Bénard and the English physicist Lord Rayleigh [1] [2] around the beginning of the 20th century. Since then, numerous studies investigated convective flows in different configurations in an experimental as well as theoretical and numerical way. As for example,

Maystrenko et al. [3] investigate the boundary layer thickness of a RB convection in air. Complementary to [3] , Ebert et al. [4] and du Puits et al. [5] measure the temperature distribution and local heat flux of a convective flow in a rectangular enclosure. Shishkina et al. [6] analyse the thermal dissipation rate and the development of plumes in a cylindrical RB cell with help of a Direct Numerical Simulation (DNS) for different Rayleigh numbers. The purpose of the presented experimental and numerical study is to investigate how the turbulent structures inside the fluid are possibly changed by a Coriolis force affecting the fluid inside the setup similar to a twister or hurricane in the atmosphere. Concerning the numerical study, a compressible Large-Eddy Simulation (LES) is performed.

2. Test Case Configuration

The experimental RB cell consists of a rectangular, air-filled container with horizontal, heated walls. The container is heated isothermally from below and cooled from above with a constant temperature difference between both walls DT = T_hot – T_cold. The container has a length (L) of 0.58 m, a height (H) of 0.2 m and a depth (D) of 0.58 m. The sidewalls consist of polymethyl methacrylate (PMMA) and have all a thickness of 0.01 m. Despite an insulating effect of the PMMA side walls, a possible heat loss through the side walls has to be considered. An almost atmospheric pressure condition is generated inside the cell. An overview of the centrifuge system (left picture) and a photograph (right picture) of the experiment installed in the centrifuge is presented in Figure 1.

The blue coloured parts in Figure 1, left picture, form the base frame of the centrifuge system. The green coloured parts mark the rotator shaft with two rotating arms. At the end of each arm a free running pendant is located. The experimental cell is installed at the right pendant. At the opposite pendant a counterbalance is fixed. The initial temperature field in the cell is assumed to be T = T_IF = T_cold = 293.15 K. The container can be characterised by the parameters of the Rayleigh number Ra, the Prandtl number Pr, the Nusselt number Nu and its aspect ratios. The mentioned parameters are defined as

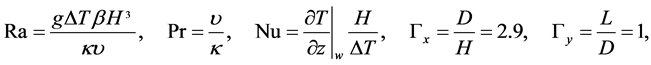(1)

where is the gravitational acceleration, 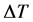the temperature difference between the hot and cold wall, β the thermal expansion rate, 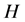the height of the container, 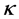the thermal diffusivity coefficient, the kinematic viscosity and 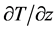the temperature gradient directly at the cold/hot wall (marked by index “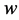”). The Nusselt number characterises the heat flux in the container. All parameters are defined on the mean temperature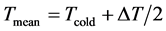. The Prandtl number lies at Pr = 0.71. If a critical value of temperature difference is reached, the fluid starts moving controlled by DT. To investigate the influence of a Coriolis force field on the turbulent structures inside the fluid, two different modes are analysed. First, the RB cell is studied in a non-rotation mode. Second, the RB cell is analysed while rotating uniformly under hyper-gravity. The rotational movement of the test cell causes relative accelerations and a higher gravitational force of g_res = 1.4 g acting on the fluid. Thus, different Rayleigh numbers are realised in both modes. In case of the non-rotation mode and DT = 3 K a Rayleigh-number of Ra = 2.33 × 10⁶ is realised, for it lies at In case of the rotation mode and DT = 3 K a Rayleigh-number of Ra = 3.29 × 10⁶ is realised, for DT = 60 K it lies at Ra = 4.32 × 10⁷. Figure 2 displays in the left picture a sketch of the test case installed in the centrifuge with relevant geometrical lengths L₁ = 3.724 m, L₂ = 4.72 m, L₃ = 0.361 m, L₄ = 1.411 m, L₅ = 0.4 m, L₆ = 5.1030 m, height H = 2.75 m, deflection angle α = 46.167˚ and two sensors S₁, S₂. The centrifuge system rotates with 13.704 revolutions per minute (rpm). The experimental setup has a total weight of 107.5 kg. It is helpful to divide the complete setup in two different systems. 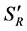The system of the RB cell, marked by and 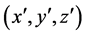in the following, is relative rotating to the inertial system of the centrifuge axis, marked by 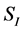and (x, y, z). The right picture in Figure 2 shows a close-up sketch of the RB cell installed in the centrifuge.

The Computational Test Case

In the 3-dimensional numerical simulation presented, the computational geometry of the container is analogously chosen to the experimental cell and displayed schematically in Figure 3, left picture. The lateral walls are modelled with a condition of adiabatic walls. The velocity field at all walls is zero due to a non-slip-condi- tion. The total pressure is considered by a zero gradient-option at all walls. The initial pressure field is assumed to be constant at 1 × 10⁵ Pa.

Figure 1. Left: Overview of the centrifuge system. Right: Photograph of the experimental RB cell installed in the centrifuge.

Figure 2. Left: Sketch of the experimental cell installed in the pendant of one rotating arm (system S_I). Right: Close-up of the RB cell (system).

Figure 3. Left: Configuration of the computational geometry. Right: Computational mesh resolution with (200 × 200 × 110) cells.

The simulation assumes a non-Boussinesq fluid. Temperature dependent fluid properties are calculated by the Sutherland model [7] . The computational mesh consists of a structured Cartesian grid with 27 blocks. It contains of (200 × 200 × 110) cells in -direction (s. Figure 3, right picture). All relevant turbulent scales are resolved and no wall functions have to be considered in the numerical model. In the middle of the geometry, large flow scales are dominant, therefore, the mesh has a coarser resolution in this region. Density changes due to temperature differences are considered in the numerical method by a compressible coupled model. The numerical method of the compressible LES used in this study was validated and described in detail in [8] .

3. Results

3.1. Velocity Structure Visualisation in the Experiment

To record the flow profile in the experiment, the flow is visualised by tracer particles of magnesium carbonate (MgCO₃). Only visualised data is estimated at this point from the experiment. A camera, which is fixed in front of the container at point K (see Figure 2 and Figure 4, right picture), records the moving flow particles.

An overview of the estimated flow region in the experimental cell as well as a sketch of the camera installation are illustrated in Figure 4. The recorded videos of the fluid movement are estimated on basis of a Particle Image Velocimetry (PIV) as it is stated in [9] . Because of a significantly varying image contrast, only a small region of the recorded videos could be estimated on basis of the PIV method (see Figure 4 left picture, red dashed rectangle). The estimated region has a height of 0.15 m and a width of 0.12 m. The flow resistance and inertia of the tracer particles should not exceed a critical value and have the same density as air. It is assumed that, in an ideal case, a tracer particle can be modelled by a spherical object. The flow resistance of a spherical particle can be circumscribed for a 2-dimensional case by the law of Stokes

(2)

where μ is the dynamic viscosity of air, r the radius of the spherical particle and u its approaching velocity. The highest realisable temperature difference between the heated walls is DT = 60 K the lowest one is. Thus, regarding these temperatures, one can assume the following parameters

(3)

with a supposed mean approaching velocity. With help of Equation (2) it is

(4)

Hence, the used tracer particles shall have at most a radius of which is fulfilled in this study. A possible influence of the tracer particles on the flow structures can be neglected because it is

(5)

where St is the stokes number and H the height of the setup. The sketches in Figure 5 picture possible displacements of a fluid particle in the RB cell due to an acting Coriolis force.

Figure 4. Left: Region of estimated flow structures in the experimental cell (red dashed rectangle). Right: Sketch of the container-camera installation in the experiment.

Figure 5. Possible displacements of a fluid particle in the container due to an acting Coriolis force.

If a particle is moving parallel to the rotation axis of the centrifuge, no effect of an acting Coriolis force can be seen. In all other cases a Coriolis acceleration affects the flow movement inside the cell. The left sketch in Figure 5 pictures a displacement of a fluid particle which is moving along the -axis of the container. In this case, ω × u points in direction of the -axis. The Coriolis acceleration points then in negative direction of the -axis. As a result, the particle will be displaced also in this direction. Combining this effect with the centrifugal effect, the particle will additionally be displaced in negative direction of the -axis. The right sketch in Figure 5 shows a displacement of a particle moving in the -plane. This movement points perpendicular relative to the angular velocity vector ω. Therefore, the Coriolis acceleration acts perpendicular to ω and u. It makes an angle of - π/2 with the -plane and has a vertical (marked by) and a horizontal component (marked by). The horizontal component displaces the particle from a straight line to the right. For a movement in the -plane, this component points always right relative to the direction of motion. The particle will be displaced in negative direction of the -axis. Due to this component, hurricanes or whirlwinds are generated in the atmosphere. The influence of the vertical component is small compared to the acceleration of gravity. The presented results in Figure 6 show the 2-dimensional velocity field estimated at a plane located parallel to the longitudinal axis of the container at in distance to the container centre). The results are estimated with help of the PIV method. Note that the scales of the axes stand only for the location of a detected particle in the estimated region and not for the dimension of the estimated region itself. The results display for all cases the same estimated region, only the number of detected particles varies from case to case. Each entry in the 2-dimensional flow field stands for a mean velocity direction vector of one detected particle at the particular location. For Ra = 3.29 × 10⁶, the PIV method detected more particles in the same estimated region than in case of the other results. Thus, one obtains a more “compact” velocity field. Note that it was not possible to obtain quantitative measured data from the experimental setup in this study. Only visualised data could be obtained. Measured values of fluid properties inside the container may be a possible step in future works. The red coloured arrows are added additionally in Figure 6 to clarify the main flow directions. In the non-rotation mode, large-scale flow structures, which are typical for a turbulent RB convection, can be seen. The increase of turbulent structures caused by the Coriolis acceleration is clearly visible. The turbulence production seems to be higher for Ra = 3.29 × 10⁶ than for Ra = 4.32 × 10⁷. Small spatial scales of flow structures as well as visible vortex structures appear in case of Ra = 3.29 × 10⁶. For Ra = 4.32 × 10⁷ these turbulent structures become larger and seem to be more regular.

3.2. Nusselt Number Values Obtained in the Simulated Process

In the study of King et al. in [10] boundary layers of rapidly rotating convection cells are investigated for different Rayleigh and Prandtl numbers in a numerical as well as experimental study. The numerical study uses an incompressible simulation. A stabilising effect of the Coriolis force on the convection is stated. The results of [10] obtained in the non-rotating mode agree for a Prandtl number of (water) and an Ekman number of (which is closest to the properties of this study) with a given Nu-Ra correlation law of Nu = 0.16 Ra^2/7. In the rotation mode, the experimental and numerical data lie beneath the given correlation law for smaller Rayleigh numbers, but converge with increasing Rayleigh numbers to the given Nu-Ra correlation law.

In this study, the LES performed uses a compressible coupled model. The analysed fluid is air and the Prandtl number lies at As mentioned above, the presented LES was validated in [8] , amongst others, on the basis of theoretical Nu-Ra power laws stated in [11] and updated in [12] . The time- and area-averaged Nusselt number values obtained in the numerical study at the cold/hot wall are plotted in Figure 7 together with the in [10] stated correlation law (red solid line) and a Nu-Ra power law formulated in [12] (blue solid line). The Nusselt number values lie in both modes and at both walls between both given laws. The values of the non-rotation mode agree very well with the power law of [12] at the hot wall. For smaller Rayleigh numbers, the values at the cold wall agree also with [12] , but converge with increasing Rayleigh numbers even to the law of [10] . The values in the rotation mode are smaller than the values in the non-rotation mode, but converge to the former with increasing Rayleigh numbers. At the cold wall higher values are visible than at the hot wall. With increasing Rayleigh numbers these values approximate the law of [10] . With further increasing Rayleigh numbers, the cold wall values would probably exceed the law of [10] . The Nusselt number values estimated in the study of [10] lie above the values of this study which is probably caused by different properties and setups of both studies. A higher heat transmission in the rotation mode is not necessarily expected. Due to the rotational movement of the cell, the turbulence production inside is indeed higher, but the flow structures are smaller and more irregular compared to the non-rotation mode as we will see in the next section.

Figure 6. Time-averaged 2-dim. velocity field. Experimental results (PIV). Plane located at. Experimental study. Top row: DT = 3 K. Bottom row: DT = 60 K.

Figure 7. Nusselt number versus Rayleigh number. Left: Cold wall. Right: Hot wall. (black dashed line with pluses): rotation mode. -×-× (black solid line with crosses): non-rotation mode. Red solid line: scaling law of [10] . Blue solid line: results of [12] .

3.3. Velocity Structures Estimated in the Simulated Process

In the study of [10] , a rapidly rotating convection cell is investigated in an incompressible numerical simulation. Gravity and the rotation axis of the cell are both vertical. It is observed that a rapidly rotating convection is typically organised by the Coriolis force into tall, thin, coherent convection columns that are aligned with the rotation axis [10] . In the presented study, the angular velocity of the centrifuge is chosen as ω = 1.435 rad/s. Furthermore, the rotation axis of the centrifuge is also vertical as gravity, but the container itself is turned by an angle of α = 46.167˚ relative to the rotation axis of the centrifuge. Consequently, the rotation axis is turned relative to the vertical axis of the container. This aspect has an additionally effect on the development of flow structures inside the fluid due to an acting influence of gravity component g which points now in an angle α relative to the heated walls and one of the perpendicular acting component g_res (see Figure 2, right picture). On the basis of DT = 3 K and a top view of the container, instantaneous snapshots of mean velocity structures in both modes are displayed in Figure 8. As in [10] , the velocity structures in the rotation mode are axially aligned and tall, thin, coherent convection structures appear. But, due to the turned rotation axis, the arrangement

Figure 8. Instantaneous snapshots of mean velocity structures in the container, top view. ∆T = 3 K. Left: Non-rotation mode. Middle and Right: Rotation mode, components.

of velocity structures show a wave-like character. In comparison to a non-rotating RB cell (left picture in Figure 8) no typical large-scale convection cells appear. The velocity structures seem to be smaller, mixed and more irregular. Compared to the non-rotating RB cell a stabilising effect of the Coriolis force could not be observed directly.

4. Conclusion

An experimental and a numerical study were performed for a turbulent RB convection in an air-filled enclosed container where the horizontal walls were heated isothermally, but with a constant temperature difference. The setup was accelerated in a large-scale centrifuge to investigate a possible influence of a Coriolis force on the development of turbulent structures inside the fluid. Compared to a non-rotating RB cell, which shows typically large-scale convection cells, the velocity structures in the rotation mode seemed to be smaller, mixed and more irregular. Furthermore, the development of turbulent structures rose. However, the structures became larger and seemed to be more regular with increasing Rayleigh numbers. Higher Nusselt number values could not be observed in the rotation mode compared to the non-rotation mode. Thus, comparing the rotating RB cell directly to the non-rotating cell, a stabilising effect of the Coriolis force could not be observed in both studies.

Acknowledgements

This study was funded by the Zentrale Forschungsförderung of the University Bremen.

Nomenclature

Roman Symbols

a_c: Coriolis acceleration vector [m/s²]

a,_ZF: Centrifugal acceleration vector in point A [m/s²]

a, _ZP: Centripetal acceleration vector in point A [m/s²]

g: Gravitational acceleration vector [m/s²]

u: Approaching velocity of a tracer particle [m/s]

m: Mass [kg]

x, y, z: Cartesian coordinates with respect to system S_I

x', y', z': Cartesian coordinates with respect to system S'_R

D: Depth of the RB cell [m]

F_w: Flow resistance [N]

H: Height of the RB cell setup [m]

L: Length of the RB cell [m]

L₁,...L₆: Lengths in the centrifuge system [m]

S_I: Inertial system

S'_R: Relative to S_I rotating system

S₁, S₂: Sensors in the centrifuge system

T: Temperature [K]

T_mean: Mean temperature between heated walls [K]

: Temperature gradient at heated walls [K/m]

r: Radius of a tracer particle [m]

V: Volume of a fluid particle [m³]

Greek Symbols

α: Angle [°]

β: Thermal expansions coefficient [1/K]

μ: Dynamic viscosity [kg/ms]

ν: Kinematic viscosity [m²/s]

κ: Thermal diffusivity coefficient [m²/s]

ρ: Density [kg/m³]

ω: Angular velocity vector [rad/s]

ΔT: Temperature difference between heated walls [K]

Dimensionless numbers

Nu: Nusselt number

Ra: Rayleigh number

Pr: Prandtl number

Γ: Aspect ratio

St: Stokes number

NOTES

^*Short paper.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Bénard, H. (1900) Les tourbillons cellulaires dans une nappe liquide. Revue Générale des Sciences Pures et Appliquées, 11, 1261-1271, 1309-1328.
[2]	Rayleigh, Lord (1916) On the Convective Currents in a Horizontal Layer of Fluid When the Higher Temperature Is on the under Side. Philosophical Magazine, Series 6, 32, 529-546.
[3]	Maystrenko, A., Resagk, C. and Thess, A. (2007) Structure of the Thermal Boundary Layer for Turbulent Rayleigh- Bénard Convection of Air in a Long Rectangular Enclosure. Physical Review E, 75, 066303-1-066303-11. http://dx.doi.org/10.1103/PhysRevE.75.066303
[4]	Ebert, A., Resagk, C. and Thess, A. (2008) Experimental Study of Temperature Distribution and Local Heat Flux for Turbulent Rayleigh-Bénard Convection of Air in a Long Rectangular Enclosure. Journal of Heat and Mass Transfer, 51, 4238-4248. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2008.01.017
[5]	Du Puits, R., Resagk, C., Tilgner, A., Busse, F.H. and Thess, A. (2007) Structure of Thermal Boundary Layers in Turbulent Rayleigh-Bénard Convection. Journal of Fluid Mechanics, 572, 231-254. http://dx.doi.org/10.1017/S0022112006003569
[6]	Shishkina, O. and Wagner, C. (2006) Analysis of Thermal Dissipation Rates in Turbulent Rayleigh-Bénard Convection. Journal of Fluid Mechanics, 546, 51-60. http://dx.doi.org/10.1017/S0022112005007408
[7]	Sutherland, W. (1893) The Viscosity of Gases and Molecular Force. Philosophical Magazine, Series 5, 36, 507-531. http://dx.doi.org/10.1080/14786449308620508
[8]	Zimmermann, C., Groll, R. and Rath, J.H. (2012) Modelling Turbulent Heat Transfer of a Rayleigh-Bénard Problem with Compressible Large-Eddy Simulation. In: Hanjalic, K., Nagano, Y., Borello, D. and Jarkirlic, S., Eds., Proceedings of the Seventh International Symposium On Turbulence, Heat and Mass Transfer, ICHMT, Begell House Inc., West Redding, USA, 615-623. http://dx.doi.org/10.1615/ICHMT.2012.ProcSevIntSympTurbHeatTransfPal.480
[9]	Mori, N. and Chang, K.A. (2002) Introduction to MPIV-PIV Toolbox in MATLAB® - Version 0.965, http://www.oceanwave.jp/softwares/mpiv/index.php?FrontPage
[10]	King, E.M., Stellmach, S., Noir, J., Hansen, U. and Aurnou, J.M. (2009) Boundary Layer Control of Rotating Convection Systems. Nature, 457, 301-304. http://dx.doi.org/10.1038/nature07647
[11]	Grossmann, S. and Lohse, D. (2000) Scaling in Thermal Convection: An Unifying Theory. Journal of Fluid Mechanics, 407, 27-56. http://dx.doi.org/10.1017/S0022112099007545
[12]	Stevens, R.J.A.M., van der Poel, E.P., Grossmann, S. and Lohse, D. (2013) The Unifying Theory of Scaling in Thermal Convection: The Updated Prefactors. Journal of Fluid Mechanics, 730, 295-308. http://dx.doi.org/10.1017/jfm.2013.298