Coherence Modified for Sensitivity to Relative Phase of Real Band-Limited Time Series ()
1. Introduction
In this paper, we examine the well-known formula for the frequency-dependent coherence 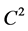 between two time series and argue that it is not well-suited for quantifying the similarity of band-limited data. Using a time domain-based analysis, we identify a critical step in the development of the traditional algorithm, which we show is inappropriate in the band-limited case, and propose an alternative that leads to the definition of a new quantity
between two time series and argue that it is not well-suited for quantifying the similarity of band-limited data. Using a time domain-based analysis, we identify a critical step in the development of the traditional algorithm, which we show is inappropriate in the band-limited case, and propose an alternative that leads to the definition of a new quantity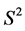 , which while having a definition similar to
, which while having a definition similar to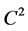 , is better behaved. We then use both synthetic tests and analytic methods to elucidate the behavior of
, is better behaved. We then use both synthetic tests and analytic methods to elucidate the behavior of , and show that it is a viable alternative to
, and show that it is a viable alternative to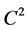 . Our belief is that the choice of time series analysis technique should be guided by the properties of the data; one analyzes time series in a way designed to best extract knowledge from them. One should always be willing to adapt an analysis method to achieve this goal.
. Our belief is that the choice of time series analysis technique should be guided by the properties of the data; one analyzes time series in a way designed to best extract knowledge from them. One should always be willing to adapt an analysis method to achieve this goal.
The issue considered here is how best to quantify the similarity between time series that are 1) real (as contrasted to complex) and 2) band-limited (in the sense of being nearly monochromatic). Such time series constitute important special cases because most natural phenomena are described using real numbers and many are dominated by a single period of oscillation. For example, the daily period often contributes strongly to physiological and meteorological signals, the annual period to environmental and climatic signals, the precessional period (25.7 ka) [1] to sedimentary and paleontological signals, and so forth. Furthermore, commonly-used techniques such as multiple window coherence analysis [2] , where two long time-series are divided into a sequence of shorter pairs before coherence analysis is performed, may accentuate the degree to which a single period of oscillation dominates the signal.
An important property of nearly-monochromatic signals is their relative phase. Whether two time series that are in-phase (as in Figure 1(a)) or out-of-phase (as in Figure 1(b)) may be important, for example, from the perspective of an analyst trying to unravel the dynamics of the underlying causative processes.
Traditional coherence analysis [3] has very limited application in this case, because of the well-known insensitivity of coherence to relative phase. The coherence of two sinusoidal time series of the same period is always unity, irrespective of their relative phase. Simply put, coherence does not distinguish a sine from a cosine. Given the general usefulness of coherence in other settings, it is well to ask why it “fails” in this special case and whether it can be modified to produce what may, in some circumstances, be a more useful measure of similarity.
When asking why any quantity encountered in time series analysis, such as coherence, behaves in a certain way, one must contend with the fact that most, if not all, such quantities can be derived from several different perspectives. Any answer will probably make sense only from one of these points of view. Consider, for example, the estimated mean of a time series. This deceptively simple quantity can be understood, alternately, as arising through the minimizing of error (a deterministic derivation) [4] or through the maximizing of likelihood (a probabilistic derivation) [5] or through the maximization of importance (an informational derivation) [6] to name just a few. The answer to a question concerning the estimated mean, say for example, whether it should always be bounded by the smallest and largest datum, will necessarily refer to one of these perspectives. The same is true for coherence. We adopt here a deterministic perspective:
The coherence between two time series, at frequency,  , is closely-related to the zero-lag cross-correlation of band-passed versions of those time series, where the band-pass filter is one-sided and has center-frequency,
, is closely-related to the zero-lag cross-correlation of band-passed versions of those time series, where the band-pass filter is one-sided and has center-frequency,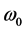 . In fact, the former is merely a normalized and squared version of the latter.
. In fact, the former is merely a normalized and squared version of the latter.
This is but one perspective among many, but one we find helpful because it brings out a relationship to the cross-correlation, another quantity useful in assessing the similarity between two time series. Cross-correlation is defined in the time-domain, as contrasted to coherence, which is defined in the frequency-domain, so the link provides complimentary information.
The appearance of a one-sided filter (Figure 2(a)), may seem counter-intuitive, because such filters are almost never used in practice, or at least not when the data are real, for they turn a real-time series into a complex one. All the band-pass filters that an analyst would commonly use are two-sided (Figure 2(b)), and so have real output. The reason for its appearance here is that the usual definition of coherence is completely general. It does not presume that the signals being compared are real, and so builds in the possibility that negative and positive
![]() (a) (b)
(a) (b)
Figure 1. (a) Two nearly-monochromatic time series (black and red curves) with the relative phase, ; (b) Same as (a), but with relative phase,
; (b) Same as (a), but with relative phase, .
.
frequency components of the time series behave completely differently from one another. This is contrast to real-time series, where they are complex conjugate pairs. However, in being general, it cannot exploit an important property of real signals: that sines and cosines are distinguishable from one another. As we show below, substituting a two-sided filter produces a version of coherence that distinguishes sines from cosines; that is, one that is sensitive to the relative phase of band-limited signals.
2. Coherence-Like Measure of Similarity Based of Cross-Correlation.
The problem we consider is how to quantify the similarity of two real, transient time series, 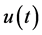 and
and , in the vicinity of a specified frequency,
, in the vicinity of a specified frequency,![]() . The strategy we adopt is to band-pass filter these time series and then to compute their zero-lag cross-correlation. The filter selects out frequencies near
. The strategy we adopt is to band-pass filter these time series and then to compute their zero-lag cross-correlation. The filter selects out frequencies near ![]() and the cross-correlation quantifies similarity, since it attains its largest value when
and the cross-correlation quantifies similarity, since it attains its largest value when ![]() (ignoring, for the moment, the issue of normalization). We denote the filtered time series as,
(ignoring, for the moment, the issue of normalization). We denote the filtered time series as, ![]() and
and ![]() where the symbol
where the symbol ![]() denotes convolution. We require the filtered time series to be purely real, so that the filter,
denotes convolution. We require the filtered time series to be purely real, so that the filter, ![]() has a two-sided Fourier transform with the symmetry,
has a two-sided Fourier transform with the symmetry, ![]() , where the tilde denotes Fourier transformation and the asterisk denotes complex conjugation. We choose a filter with a purely-real Fourier transform, built from two unit-am- plitude boxcar functions, one centered at
, where the tilde denotes Fourier transformation and the asterisk denotes complex conjugation. We choose a filter with a purely-real Fourier transform, built from two unit-am- plitude boxcar functions, one centered at ![]() and the other at
and the other at![]() , each of width
, each of width![]() . This filter does not affect Fourier components within the pass-band and completely rejects those outside of it.
. This filter does not affect Fourier components within the pass-band and completely rejects those outside of it.
The convolution, ![]() , and cross-correlation,
, and cross-correlation, ![]() , of two real time series are defined as [7] (their pages 24 and 46):
, of two real time series are defined as [7] (their pages 24 and 46):
![]() (1a)
(1a)
![]() (1b)
(1b)
Note that at zero-lag, cross-correlation is just the area beneath the product of the two time series:
![]() (2)
(2)
Note also that definition of the convolution and cross-correlation in (1a), (1b) differ only by a sign of ![]() in the
in the ![]() term. The substitution,
term. The substitution, ![]() , leads to the very useful, well-known identity,
, leads to the very useful, well-known identity, ![]()
![]() ([7] , their page 47). Applying this identify, we find that the cross-correlation of the filtered time series is:
([7] , their page 47). Applying this identify, we find that the cross-correlation of the filtered time series is:
![]() (3)
(3)
At zero lag, the cross-correlation is proportional the integral of its Fourier transform,![]() :
:
![]() (4)
(4)
Inserting (3) into (4) and using the rule that the Fourier transform of a convolution is the product of the transforms ([7] , page 115) and the rule that the transform of ![]() is
is ![]() (see Appendix) yields:
(see Appendix) yields:
![]() (5)
(5)
Here ![]() denotes the mean value of
denotes the mean value of ![]() in the frequency band,
in the frequency band,![]() . Note that
. Note that ![]()
is defined for![]() , only. The quantity
, only. The quantity ![]() is the cross-spectrum. Thus, the zero-lag cross-correla- tion of the real band-pass filtered time series depends upon the average value of the real part of their cross-spec- trum in the filter’s pass-band. The amplitude of
is the cross-spectrum. Thus, the zero-lag cross-correla- tion of the real band-pass filtered time series depends upon the average value of the real part of their cross-spec- trum in the filter’s pass-band. The amplitude of ![]() depends on the amplitude of two time series, as well as upon their degree of similarity. We remove this dependence by normalizing by the energy
depends on the amplitude of two time series, as well as upon their degree of similarity. We remove this dependence by normalizing by the energy ![]() and
and ![]() in the two time series, defined as:
in the two time series, defined as:
![]() (6)
(6)
The normalized measure of similarity, say![]() , is:
, is:
![]() (7)
(7)
Note that the quantity, ![]() , which we nickname here similarity, varies between zero and unity. It has almost exactly the functional form of the quantity called coherence, except for the taking of the real part. The imaginary part cancelled from (5) precisely because the time series are real and the filter is two-sided.
, which we nickname here similarity, varies between zero and unity. It has almost exactly the functional form of the quantity called coherence, except for the taking of the real part. The imaginary part cancelled from (5) precisely because the time series are real and the filter is two-sided.
3. Coherence Related to Zero-Lag Cross-Correlation
As asserted in the Introduction, the usual formula for coherence can be obtained simply by switching to a one-sided filter, a single unit step function of width ![]() centered at frequency
centered at frequency ![]() (where
(where![]() ). The filtered time series
). The filtered time series ![]() and
and ![]() are complex, so that one must define a cross-correlation appropriate for complex signals; that is, replace
are complex, so that one must define a cross-correlation appropriate for complex signals; that is, replace ![]() with
with ![]() in (1b). These modifications lead to a version of (7) that is exactly the usual formula for the coherence:
in (1b). These modifications lead to a version of (7) that is exactly the usual formula for the coherence:
![]() (8)
(8)
As an aside, we note that our derivations of ![]() and
and ![]() hide an inconsistency in the interpretation of
hide an inconsistency in the interpretation of ![]() as the power in the time series
as the power in the time series ![]() at frequency,
at frequency,![]() . It represents power for a complex time series but only half the power for a real one, owing to the different intervals over which frequency,
. It represents power for a complex time series but only half the power for a real one, owing to the different intervals over which frequency, ![]() , is defined. This factor of two compensates for the apparent loss of power when the real part is taken in (5).
, is defined. This factor of two compensates for the apparent loss of power when the real part is taken in (5).
4. Similarity and Coherence of Real Band-Limited Signals
Suppose that time series ![]() and
and ![]() are monochromatic, with equal frequency,
are monochromatic, with equal frequency, ![]() , but with different amplitudes,
, but with different amplitudes, ![]() and
and![]() , and relative phase,
, and relative phase,![]() :
:
![]() (9)
(9)
The similarity, ![]() , is most easily calculated using its time-domain definition. Taking, without loss of generality, the window of observation to be
, is most easily calculated using its time-domain definition. Taking, without loss of generality, the window of observation to be![]() , we have:
, we have:
![]() (10)
(10)
Thus, ![]() is unity when the two sinusoids are in-phase
is unity when the two sinusoids are in-phase ![]() and declines monotonically to zero when they are out-of-phase
and declines monotonically to zero when they are out-of-phase![]() .
.
The coherence, ![]() , is calculated by recognizing that a sine function is built up of two complex exponentials of frequency
, is calculated by recognizing that a sine function is built up of two complex exponentials of frequency ![]() and
and ![]() and that the one-sided filter selects only the one with positive frequency:
and that the one-sided filter selects only the one with positive frequency:
![]() (11)
(11)
We then find:
![]() (12)
(12)
This is the well-known result that the coherence, ![]() , is unity irrespective of the relative phase of the two sinusoids. This behavior is a consequence of the one-sided filter, which turns both
, is unity irrespective of the relative phase of the two sinusoids. This behavior is a consequence of the one-sided filter, which turns both ![]() and
and ![]() into functions proportional to the same complex exponential,
into functions proportional to the same complex exponential,![]() .
.
5. Examples
We consider the example of a sequence of nearly-monochromatic wavelets, formed by taking the product of a phase-shifted sinusoid of frequency, ![]() , and a normal envelope function of half-width,
, and a normal envelope function of half-width,![]() :
:
![]() (13)
(13)
and then by adding a small amount of uncorrelated random noise. Figures 3(a)-(c) illustrate pairs of these wavelets with different phase relationships. Note that the wavelets are not merely time-shifted versions of one another, since the position of the zeros crossings of the sinusoid (parameterized by![]() ) can and the position of the center of the envelope (parameterized by
) can and the position of the center of the envelope (parameterized by![]() ) can be independently varied. One might imagine a time series analysis scenario where
) can be independently varied. One might imagine a time series analysis scenario where ![]() represents the external forcing applied to some dynamical system, and
represents the external forcing applied to some dynamical system, and ![]() represents the response. In such a context, the distinction between these different wavelet shapes is important, say for detecting whether or not some anticipated interaction has occurred. In this case, the similarity,
represents the response. In such a context, the distinction between these different wavelet shapes is important, say for detecting whether or not some anticipated interaction has occurred. In this case, the similarity, ![]() (red curves in Figure 3(d), Figure 3(c)) is a more useful quantity than the coherence,
(red curves in Figure 3(d), Figure 3(c)) is a more useful quantity than the coherence, ![]() (black curves), since it varies strongly with the phase-relationships, whereas coherence does not.
(black curves), since it varies strongly with the phase-relationships, whereas coherence does not.
We have not performed an exhaustive analysis of the differences between ![]() and
and![]() , when they are applied to broad-band signals. The key difference is the effect of the taking of the real part:
, when they are applied to broad-band signals. The key difference is the effect of the taking of the real part:
![]() (14)
(14)
where the Fourier transforms are written in terms of their real and imaginary parts, ![]() and
and![]() . Since
. Since ![]() and
and ![]() differ by a manifestly positive amount, we are guaranteed that
differ by a manifestly positive amount, we are guaranteed that![]() . However, without further specification of the behavior or
. However, without further specification of the behavior or ![]() and
and![]() , no further characterization is possible. In the special case where both time series contain a common function
, no further characterization is possible. In the special case where both time series contain a common function![]() , so that
, so that ![]() and
and ![]() and where
and where![]() ,
, ![]() and
and ![]() are all broad-band, we find:
are all broad-band, we find:
![]() (15)
(15)
We might expect in the case that![]() , since the cross-terms are averages of functions that oscillate around zero and therefore likely to be small. Numerical tests (Figure 4) support this idea, at least for non-transient broad-band time series with a moderate degree of correlation.
, since the cross-terms are averages of functions that oscillate around zero and therefore likely to be small. Numerical tests (Figure 4) support this idea, at least for non-transient broad-band time series with a moderate degree of correlation.
6. Conclusion
In summary, we recommend this simple modification of coherence in cases where the time series that are being compared are narrow-band and where phase relationships between them are considered important. For pure sinusoids differing by phase, ![]() , it obeys the rule
, it obeys the rule![]() ; that is, similarity monotonically decreases from unity, when
; that is, similarity monotonically decreases from unity, when![]() , and to zero, when
, and to zero, when![]() . In other respects, it behaves very similarly to coherence. Finally, it has a very intuitive time-domain interpretation:
. In other respects, it behaves very similarly to coherence. Finally, it has a very intuitive time-domain interpretation: ![]() gives you exactly what you would get if you normalized each time series by the square-root of its energy, band-pass filtered each with a two-sided boxcar filter centered around frequency,
gives you exactly what you would get if you normalized each time series by the square-root of its energy, band-pass filtered each with a two-sided boxcar filter centered around frequency, ![]() , and computed their zero-lag cross-correlation.
, and computed their zero-lag cross-correlation.
Appendix
The rule that the transform of ![]() is
is ![]() is well-known, but we derive it here for completeness. The Fourier transform of
is well-known, but we derive it here for completeness. The Fourier transform of ![]() is:
is:
![]() (A1)
(A1)
Here we have utilized the substitution![]() .
.