Mean-Field Formulation of Maxwell Equations to Model Electrically Inhomogeneous and Isotropic Media ()
1. Introduction
Maxwell equations of electromagnetism were initially designed to describe classic electromagnetic phenomena in arbitrary media (such as vacuum, air, water, etc). In Maxwell formalism, the electromagnetic properties of matter are described using three standard parameters, electric conductivity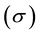 , electric permittivity
, electric permittivity 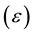 and magnetic permeability
and magnetic permeability  when the medium is isotropic. It is important to note that Maxwell theory is a mean-field theory of electromagnetism. The notions of electric conductivity and permittivity (different from that of vacuum) of a given medium do not have a physical sense at a sub-atomic level, and thus these notions only apply to a mean-field level. This is analogous to the notion of pressure and temperature in classic thermodynamics.
when the medium is isotropic. It is important to note that Maxwell theory is a mean-field theory of electromagnetism. The notions of electric conductivity and permittivity (different from that of vacuum) of a given medium do not have a physical sense at a sub-atomic level, and thus these notions only apply to a mean-field level. This is analogous to the notion of pressure and temperature in classic thermodynamics.
Many materials or living tissue are not electrically homogeneous and consist of an aggregate of different materials with different electrical properties. For example, biological media are made of cells where the cellular membrane is of very low conductivity, while different cells are separated by extracellular fluid which is highly conductive because it contains different ionic species at millimolar concentrations. Similar considerations apply to composite materials, such as amorphous solids [1] . In such cases, Maxwell equations can still be used, but the fact that the conductivity and permittivity highly depend on space, complicates its application. In the present paper, we will review this situation and show the type of expressions that can be used in electrically inhomogeneous media.
An alternative and complementary approach is to derive a mean-field version of Maxwell equations, by performing spatial averages over some reference volume. If the volume is chosen such as to average out the spatial inhomogeneities of conductivity and permittivity, then one can obtain a useful description to model inhomogeneous media. In this paper, we will review such a mean-field formulation of Maxwell equations, and delineate the differences with the Maxwell theory in a homogeneous medium. Note that most of the models used in biological systems neglect the electrical inhomogeneity of the tissue.
2. Microscopic Model of Electrically Inhomogeneous Isotropic Media
We describe here media that are electrically inhomogeneous and isotropic, which can be caused for example by a mixture of compounds having different electric conductivity and permittivity1. This can occur for example in solid inhomogeneous materials such as amorphous solids [1] or in biological media such as brain tissue, in which different cellular processes are densely packed [2] , and the extracellular space consists of a mixture of membranes of very low conductivity and extracellular highly conductive fluids. Microscopically, this means that the conductivity and permittivity are functions of spatial coordinates , which will be noted by
, which will be noted by 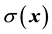 and
and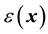 , respectively.
, respectively.
To model such microscopically inhomogeneous isotropic media, one starts from Maxwell equations, and in particular Maxwell-Gauss law:
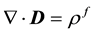
and Ampere-Maxwell law:
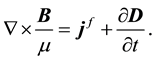
If we assume that magnetic permeability is constant in such inhomogeneous media, we obtain:
 (1)
(1)
where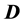 ,
, 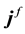 and
and 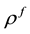 are respectively the electric displacement, the free-charge density and free-charge charge density in the medium.
are respectively the electric displacement, the free-charge density and free-charge charge density in the medium.
If we further assume that the medium is linear, the equations linking the electric field 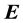 with electric displacement
with electric displacement 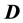 and the free-charge current density
and the free-charge current density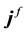 , are given by:
, are given by:
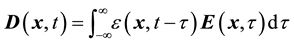 (2)
(2)
and
![]() (3)
(3)
In this model, the electric parameters ![]() and
and ![]() take their “microscopic” values and are assumed to be independent of time, but depend on spatial coordinates. In Fourier-transformed coordinates, the above equations are respectively
take their “microscopic” values and are assumed to be independent of time, but depend on spatial coordinates. In Fourier-transformed coordinates, the above equations are respectively
![]()
and
![]()
where ![]() where
where ![]() is the frequency.
is the frequency.
It is important to note that, in this microscopic model, ![]() and
and ![]() are real numbers, but this is not necessarily the general case. A real electric conductivity (in Fourier-transformed coordinates) is equivalent to assume that the calorific dissipation and polarization are fast enough so that there is no phase delay between the electric field and the current density produced, the electric displacement and the electric field. This is the case for the low frequency range. For electric phenomena in biological media such as cerebral cortex, this hypothesis applies to frequencies smaller than about 1000 Hz [3] - [6] .
are real numbers, but this is not necessarily the general case. A real electric conductivity (in Fourier-transformed coordinates) is equivalent to assume that the calorific dissipation and polarization are fast enough so that there is no phase delay between the electric field and the current density produced, the electric displacement and the electric field. This is the case for the low frequency range. For electric phenomena in biological media such as cerebral cortex, this hypothesis applies to frequencies smaller than about 1000 Hz [3] - [6] .
Another approximation to Maxwell equations is the quasi-static electric approximation, which consists of de-coupling electric and magnetic variables (this also equivalent to postulating a low number of charge carriers, and that they move at slow speed![]() ). Under this approximation, we can consider
). Under this approximation, we can consider ![]() for low frequencies (smaller than about 1000 Hz) and
for low frequencies (smaller than about 1000 Hz) and![]() . In such conditions, the complex Fourier transform of Equation (1) can be written as:
. In such conditions, the complex Fourier transform of Equation (1) can be written as:
![]()
Consequently, we have
![]() (4)
(4)
This last equation can be used to calculate the electric potential in any point of space in an non-homogeneous medium. It was derived previously in the context of calculating the electric potential from brain tissue [3] . It is general enough to calculate the propagation of the extracellular potential in media which can have a complex or inhomogeneous structure, as well as frequency dependent electric parameters.
It is important to note that Equation (4) reduces to Laplace equation ![]() when the medium is homogeneous with respect to
when the medium is homogeneous with respect to ![]() and
and![]() . Thus, Equation (4) can be seen as a generalization of Laplace equation for media where
. Thus, Equation (4) can be seen as a generalization of Laplace equation for media where ![]() and
and ![]() are variable in space.
are variable in space.
A particular case is when the ratio ![]() is independent of position. In that case, the electric potential does not satisfy Laplace equation
is independent of position. In that case, the electric potential does not satisfy Laplace equation![]() , but obeys
, but obeys
![]()
When ![]() is constant everywhere. This ratio is often called the Maxwell-Wagner time of the dielectric, written as
is constant everywhere. This ratio is often called the Maxwell-Wagner time of the dielectric, written as![]() . Note that steep spatial variations of
. Note that steep spatial variations of ![]() imply that
imply that ![]() can be very large, which in turn implies solutions very different from the solutions of Laplace equation.
can be very large, which in turn implies solutions very different from the solutions of Laplace equation.
This “microscopic” model was used to calculate the extracellular electric potential (also called local field potential or LFP), generated by neurons in brain tissue [3] . It was used to simulate the effect of different spatial profiles of conductivity and permittivity around neurons. It was found that according to the profile of ![]() and
and![]() , one can have a high-pass or low-pass filter, but in general when
, one can have a high-pass or low-pass filter, but in general when ![]() is high at short distances and decays with larger distances, a low-pass filter is observed. For example, with an exponentially decaying conductivity, a low-pass filter attenuates more strongly the fast frequencies compared to low frequencies. A simulation of the LFP generated showed that the extracellular waveform of an action potential changes as the distance to the source is increased [3] . Such frequency filtering was observed experimentally, and thus, this model shows that part of the observed frequency filtering could be due to the spatial inhomogeneity of the brain tissue.
is high at short distances and decays with larger distances, a low-pass filter is observed. For example, with an exponentially decaying conductivity, a low-pass filter attenuates more strongly the fast frequencies compared to low frequencies. A simulation of the LFP generated showed that the extracellular waveform of an action potential changes as the distance to the source is increased [3] . Such frequency filtering was observed experimentally, and thus, this model shows that part of the observed frequency filtering could be due to the spatial inhomogeneity of the brain tissue.
3. Macroscopic Model of Electrically Inhomogeneous Media
In principle, it is sufficient to solve Equation (4) in the extracellular medium to simulate the electric potential in any inhomogeneous medium. However, if the medium has a complex spatial structure, it may be tedious to assign the space dependence of the electric parameters ![]() and
and![]() . One way to solve this problem is to consider a macroscopic or mean-field approach at a larger scale, in which the electric parameters will be considered as constant in space, but are the result of a microscopic mixture of materials of different resistivity and permittivity.
. One way to solve this problem is to consider a macroscopic or mean-field approach at a larger scale, in which the electric parameters will be considered as constant in space, but are the result of a microscopic mixture of materials of different resistivity and permittivity.
The construction of a mean-field model of Maxwell equations is greatly facilitated by the fact that these equations are invariant under change of scale if electric parameters are renormalized appropriately (see details in refs. [7] and [8] ). This approach is also justified by the fact that the values measured experimentally are averaged values, which precision depends on the measurement technique. Ideally, one should have a formalism that can integrate those macroscopic measurements. Thus, we will build a macroscopic model, where we take spatial averages of Equation (4), and make a continuous approximation for the spatial variations of these average values (see details in ref. [6] ).
We start by defining macroscopic electric parameters, ![]() and
and![]() , by taking an average of the “microscopic” electric parameters over some volume
, by taking an average of the “microscopic” electric parameters over some volume![]() :
:
![]()
and
![]()
We usually assume that ![]() is much smaller than the total volume of the medium, but larger than the typical size of the spatial inhomogeneities. For example,
is much smaller than the total volume of the medium, but larger than the typical size of the spatial inhomogeneities. For example, ![]() is of the order of
is of the order of ![]() to
to ![]() for brain tissue, in which the spatial variations occur at a
for brain tissue, in which the spatial variations occur at a ![]() scale, while the total size of the tissue is of the order of centimeters.
scale, while the total size of the tissue is of the order of centimeters.
Taking advantage of the fact that the average values of electric parameters are statistically independent of the mean value of the electric field, we obtain:
![]()
where ![]() is the generalized current density (also called total current density), the first term in the
is the generalized current density (also called total current density), the first term in the
right hand represents the “dissipative” contribution, and the second term represents the “reactive” contribution (reaction from the medium, such as polarization). Here, all physical effects, such as diffusion, resistive and capacitive phenomena, are integrated into the frequency dependence of ![]() and
and![]() . The second term translates the fact that there is an inertia time for polarization (also called Maxwell-Wagner time), because the charges do not move instantaneously. This implies that the electric field will take a characteristic time to settle; this time is given by the Maxwell-Wagner time of the region in which the average is taken (see details in ref. [9] and for applications to biological membranes, see ref. [4] ).
. The second term translates the fact that there is an inertia time for polarization (also called Maxwell-Wagner time), because the charges do not move instantaneously. This implies that the electric field will take a characteristic time to settle; this time is given by the Maxwell-Wagner time of the region in which the average is taken (see details in ref. [9] and for applications to biological membranes, see ref. [4] ).
Note that the generalized current density was used in the expression above because this density can be different than zero even in the absence of charges (because![]() ) [10] .
) [10] .
Taking the complex Fourier transform of![]() , we obtain:
, we obtain:
![]() (5)
(5)
where ![]() is the complex macroscopic conductivity. Thus, in this model, we consider that the imaginary part of this complex macroscopic conductivity originates solely from capacitive effects. This is equivalent to assume that the calorific dissipation caused by collisions between charges and various obstacles is much faster than the variations of the electric field. Here again, this is valid only for the low frequency range (smaller than about 1000 Hz for cerebral cortex tissue).
is the complex macroscopic conductivity. Thus, in this model, we consider that the imaginary part of this complex macroscopic conductivity originates solely from capacitive effects. This is equivalent to assume that the calorific dissipation caused by collisions between charges and various obstacles is much faster than the variations of the electric field. Here again, this is valid only for the low frequency range (smaller than about 1000 Hz for cerebral cortex tissue).
It is important to note that in the literature [11] , the complex permittivity is defined by the following relation:
![]() (6)
(6)
where the subscript ![]() distinguishes from the real-valued permittivity
distinguishes from the real-valued permittivity![]() . We can then write
. We can then write
![]() (7)
(7)
Because ![]() and
and![]() , the expressions above (Equation (7)) can also be written in the form:
, the expressions above (Equation (7)) can also be written in the form:
![]() (8)
(8)
Note that this last equation shows that the generalized current is conserved, which is consistent with ![]() because of the mathematical identity
because of the mathematical identity![]() .
.
Comparing this equation with Equation (4), we can see that the same mathematical form is obtained here for the macroscopic model, but with frequency-dependent electric parameters (see details in ref. [8] ). This form invariance will allow us to introduce different phenomena, such as surface polarization or ionic diffusion, by including an ad hoc frequency dependence in ![]() and
and![]() . The physical causes of this macroscopic frequency dependence is that the medium is microscopically non-neutral (although it is macroscopically neutral). Such a local non-neutrality was already postulated in a previous model of surface polarization [4] . This situation cannot be accounted by Equation (4) if
. The physical causes of this macroscopic frequency dependence is that the medium is microscopically non-neutral (although it is macroscopically neutral). Such a local non-neutrality was already postulated in a previous model of surface polarization [4] . This situation cannot be accounted by Equation (4) if ![]() and
and ![]() are frequency independent (in which case
are frequency independent (in which case ![]() when
when![]() ). Thus, including the frequency dependence of these parameters enables the model to capture a much broader range of physical phenomena.
). Thus, including the frequency dependence of these parameters enables the model to capture a much broader range of physical phenomena.
Finally, in the macroscopic model derived above, a fundamental point is that the frequency dependencies of the electrical parameters ![]() and
and ![]() cannot take arbitrary values, but are related to each-other by the Kramers-Kronig relations [7] [11] - [13] . These relations come from the fact that the imaginary part of the complex macroscopic conductivity is related to the permittivity (Equation (5)):
cannot take arbitrary values, but are related to each-other by the Kramers-Kronig relations [7] [11] - [13] . These relations come from the fact that the imaginary part of the complex macroscopic conductivity is related to the permittivity (Equation (5)):
![]() (9)
(9)
and
![]() (10)
(10)
where principal value integrals are used. These equations are valid for any linear medium (i.e., when Equations (2) and (3) are linear). These relations will turn out to be critical to relate the model to experiments, as shown previously [7] .
This “macroscopic” model was used to investigate the genesis of extracellular potentials by neurons, taking into account the complex structure of the extracellular medium [5] . The macroscopic measurements of extracellular conductivity and permittivity in brain tissue [14] can be integrated directly in this formalism. By doing this, it was shown that ionic diffusion (and its associated “Warburg impedance”) can account for most of the frequency dependence of ![]() and
and ![]() found experimentally, and including this dependence into the equation for generating extracellular potentials (Equation (5)) leads to extracellular potentials with the typical
found experimentally, and including this dependence into the equation for generating extracellular potentials (Equation (5)) leads to extracellular potentials with the typical ![]() power spectral structure of these potentials (see ref. [5] for details). Other models have been proposed for
power spectral structure of these potentials (see ref. [5] for details). Other models have been proposed for ![]() scaling at high frequencies [15] , but the present model is the only one that accounts for the frequency scaling of extracellular potentials over the whole frequency range. This model shows that ionic diffusion provides a physical mechanism that is capable of explaining a large range of experimental observations, and that a macroscopic model is the right formalism to investigate such properties.
scaling at high frequencies [15] , but the present model is the only one that accounts for the frequency scaling of extracellular potentials over the whole frequency range. This model shows that ionic diffusion provides a physical mechanism that is capable of explaining a large range of experimental observations, and that a macroscopic model is the right formalism to investigate such properties.
4. Discussion
In this paper, we have overviewed two formalisms to model the electrical behavior of electrically inhomogeneous media. The first formalism, which we called “microscopic” considers the specific case of media that are non-homogeneous, in which the electric parameters ![]() and
and ![]() are strongly dependent on position. In this case, one must return to Maxwell equations to derive the correct equation to calculate the electric potential. The reason is that in such media, there will be charge accumulation, and the local free-charge conservation law
are strongly dependent on position. In this case, one must return to Maxwell equations to derive the correct equation to calculate the electric potential. The reason is that in such media, there will be charge accumulation, and the local free-charge conservation law ![]() does not apply, one must take into account the displacement current
does not apply, one must take into account the displacement current
![]() (see ref. [3] ). This formalism was derived previously and was
(see ref. [3] ). This formalism was derived previously and was
shown to simulate the low-pass filtering properties of extracellular space in brain tissue [3] . However, this “microscopic” formalism cannot integrate “macroscopic” measurements of ![]() and
and ![]() [14] , nor the fact that the frequency filter deduced from experimental measurements is of
[14] , nor the fact that the frequency filter deduced from experimental measurements is of ![]() type [5] .
type [5] .
A second formalism, which we called “macroscopic”, describes the tissue at a larger coarse-graining, and in which the electric parameters will be considered as constant in space, but are the result of a mixture of different media such as fluids and membranes [6] . This formalism is similar in spirit to the “Effective medium theory” developed for inhomogeneous materials [16] . It can directly integrate the macroscopic measurements of ![]() and
and ![]() (such as from ref. [14] for biological tissues), and thus can be used to simulate a wide variety of physical mechanisms. For example, it can be used to simulate the polarization phenomena that the electric field induces on neuronal membranes; it can also be used to integrate the effect of ionic diffusion.
(such as from ref. [14] for biological tissues), and thus can be used to simulate a wide variety of physical mechanisms. For example, it can be used to simulate the polarization phenomena that the electric field induces on neuronal membranes; it can also be used to integrate the effect of ionic diffusion.
Such a mean-field approach is possible because of the scale invariance of the mathematical structure of Maxwell equations. This property allows one to renormalize the electromagnetic parameters such that, even if the microscopic parameters do not depend on frequency, the macroscopic parameters can be frequency-dependent in some media (see details in ref. [8] ). This is a consequence of the fact that the Maxwell-Wagner time is non-neg- ligible in such media. Note that some models postulate that there is no such frequency dependence, which is equivalent to neglect the Maxwell-Wagner time and consider that the charges move infinitely fast. This latter model would correspond to the simplest possible model in electromagnetism theory. We suggest here an alternative formulation which takes into account the influence of the electrical structure of the medium.
Acknowledgements
Research supported by the CNRS and the European Union (BrainScales FP7-269921, Magnetrodes FP7-600730 and the Human Brain Project).
NOTES
1We consider here media that are not ferromagnetic, so the spatial variations of magnetic permeability μ can be neglected, and μ can be considered equal to that of vacuum.