Global Attractor and Dimension Estimation for a 2D Generalized Anisotropy Kuramoto-Sivashinsky Equation ()
1. Introduction
In recent years, the infinite dimension dynamic system with high dimension has been studied extensively, and the studies have obtained many achievements [1] -[8] . The related questions of its existence and uniqueness of solutions; the existence and dimension of global attractor; the existence and attraction of inertial manifolds; finite dimension, approximate inertial manifolds and time-lag inertial manifolds are still important contents that are studied.
The celebrated Kuramoto-Sivashinsky Equation
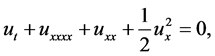 (1.1)
(1.1)
where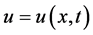 , is an Equation that for nearly half a century has attracted the attention of many researchers from various areas due to its simple but rich dynamics [9] . It first appeared in the mid-1970s by Kuramoto in the study of angularphase turbulence for a system of reaction-diffusion equations modeling the Belousov Zhabotinskii reaction in three spatial dimensions [10] .
, is an Equation that for nearly half a century has attracted the attention of many researchers from various areas due to its simple but rich dynamics [9] . It first appeared in the mid-1970s by Kuramoto in the study of angularphase turbulence for a system of reaction-diffusion equations modeling the Belousov Zhabotinskii reaction in three spatial dimensions [10] .
In a physical context, Equation (1.1) is used to model continuous media that exhibits chaotic behavior such as weak turbulence on interfaces among complex flows (quasi-planar flame front and the fluctuation of the positions of a flame front, fluctuations in thin viscous fluid films flowing over inclined planes or vertical walls, dendritic phase change fronts in binary alloy mixtures), small perturbations of a metastable planar front or interface (spatially uniform oscillating chemical reaction in a homogeneous medium) and physical systems driven far from the equilibrium due to intrinsic instabilities (instabilities of dissipative trapped ion modes in plasmas and phase dynamics in reaction-diffusion systems).
As a dynamical system the KSE is known for its chaotic solutions and complicated behavior due to the terms that appear. Namely, the 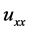 term acts as an energy source and has a destabilizing effect at a large scale, the dissipative
term acts as an energy source and has a destabilizing effect at a large scale, the dissipative 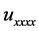 term provides dumping in small scales and, finally, the nonlinear term provides stabilization by transferring energy between large and small scales. Because of this fact, Equation (1.1) was studied extensively as a paradigm of finite dynamics in a partial differential equation. Its multi-modal, oscillatory and chaotic solutions have been investigated; its non-integrability was established via its Painlev analysis and due to its bifurcation behavior, a connection to low finite-dimensional dynamical systems is established.
term provides dumping in small scales and, finally, the nonlinear term provides stabilization by transferring energy between large and small scales. Because of this fact, Equation (1.1) was studied extensively as a paradigm of finite dynamics in a partial differential equation. Its multi-modal, oscillatory and chaotic solutions have been investigated; its non-integrability was established via its Painlev analysis and due to its bifurcation behavior, a connection to low finite-dimensional dynamical systems is established.
The generalization of KSE to two dimensions comes naturally, the two-dimensional KuramotoCSivashinsky Equation
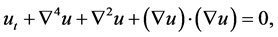 (1.2)
(1.2)
where now 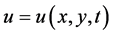 and
and  Equation (1.2) has equally attracted much attention because of the same spatiotemporal chaos properties that exhibits and its applications in modeling complex dynamics in hydrodynamics [11] . Nevertheless, due to the additional spatial dimension Equation (1.2) is very challenging and even its well-posedness is still an open problem.
Equation (1.2) has equally attracted much attention because of the same spatiotemporal chaos properties that exhibits and its applications in modeling complex dynamics in hydrodynamics [11] . Nevertheless, due to the additional spatial dimension Equation (1.2) is very challenging and even its well-posedness is still an open problem.
One generalization of Equation (1.2) which is of much interest is the anisotropic two-dimensional KuramotoCSivashinsky Equation
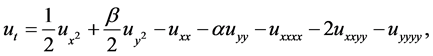 (1.3)
(1.3)
where the two real parameters 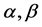 control the anisotropy of the linear and the nonlinear term, respectively, in other words, the stability of the solutions of Equation (1.3). The anisotropic two-dimensional KuramotoCSivashinsky Equation, due to the fact that it describes linearly unstable surface dynamics in the presence of in-plane anisotropy, has a wide range of applications, for instance, as a model for the nonlinear evolution of sputter-eroded surfaces and describing the epitaxial growth of a vicinal surface destabilized by step edge barriers; for further details, see the references therein, in particular [12] .
control the anisotropy of the linear and the nonlinear term, respectively, in other words, the stability of the solutions of Equation (1.3). The anisotropic two-dimensional KuramotoCSivashinsky Equation, due to the fact that it describes linearly unstable surface dynamics in the presence of in-plane anisotropy, has a wide range of applications, for instance, as a model for the nonlinear evolution of sputter-eroded surfaces and describing the epitaxial growth of a vicinal surface destabilized by step edge barriers; for further details, see the references therein, in particular [12] .
This paper focuses on the following generalization of the anisotropic KSE (1.3)
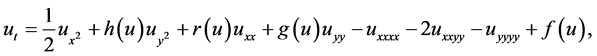 (1.4)
(1.4)
where 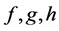 and
and 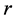 are considered as smooth functions of
are considered as smooth functions of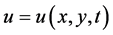 , and its study under the prism of Lie point symmetries and conservation laws [13] .
, and its study under the prism of Lie point symmetries and conservation laws [13] .
According to the above information, the paper mainly thinks about the following generalization of the anisotropic KSE (1.4)
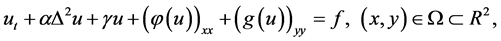 (1.5)
(1.5)
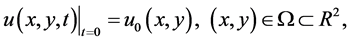 (1.6)
(1.6)
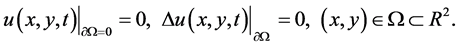 (1.7)
(1.7)
Here ![]() is bounded set;
is bounded set; ![]() is the bound of
is the bound of![]() ;
; ![]() and
and ![]() are considered as smooth functions
are considered as smooth functions
of![]() . Let
. Let![]() .
.
The following is the rest of this paper. In Section 2, we introduce some basic contents concerning global attractor. In Section 3, we obtain the existence of the global attractor, then we get the upper bound estimation of the Hausdorff and fractal dimension of the global attractor.
2. The Priori Estimate of Solution of Questions (1.5) - (1.7)
Lemma 1. Assume ![]()
![]()
![]()
![]()
![]()
![]() so
so
the smooth solution ![]() of Questions (1.5) - (1.7) satisfies
of Questions (1.5) - (1.7) satisfies
![]() (2.1)
(2.1)
Proof. We multiply ![]() with both sides of Equation (1.5) and obtain
with both sides of Equation (1.5) and obtain
![]() (2.2)
(2.2)
Here
![]()
![]()
![]()
According to Nirenberg-Gagliardo and Cauchy inequality, we obtain
![]()
From the (2.2) we obtain
![]() (2.3)
(2.3)
Using the Gronwall inequality, the (2.1) is proved.
Lemma 2. Under the condition of Lemma 1, and ![]()
![]()
![]() so the smooth solution
so the smooth solution ![]() of Questions (1.5) - (1.7) satisfies
of Questions (1.5) - (1.7) satisfies
![]() (2.4)
(2.4)
Proof. We multiply ![]() with both sides of Equation (1.5) and obtain
with both sides of Equation (1.5) and obtain
![]() (2.5)
(2.5)
Here
![]()
![]()
![]()
According to the hypothetical condition ![]() and Sobolev interpolation inequalities
and Sobolev interpolation inequalities
![]()
so
![]()
![]()
Using the Young inequality obtain
![]()
From the (2.5) we obtain
![]()
Here ![]() According to the Gronwall inequality,we can get the (2.4).
According to the Gronwall inequality,we can get the (2.4).
Lemma 3. Under the condition of Lemma 2, and ![]()
![]()
![]() so the smooth solution
so the smooth solution ![]() of Questions (1.5) - (1.7) satisfies
of Questions (1.5) - (1.7) satisfies
![]() (2.6)
(2.6)
Proof. We multiply ![]() with both sides of Equation (1.5) and obtain
with both sides of Equation (1.5) and obtain
![]() (2.7)
(2.7)
Here
![]()
By Sobolev interpolation inequality
![]()
Noticing interpolation inequalities
![]()
![]()
so
![]()
![]()
According to the Young inequality,we can obtain
![]()
From the (2.7) we obtain
![]()
By the Gronwall inequality we can get the (2.6).
Lemma 4. Under the condition of Lemma 3, and
![]()
so the smooth solution ![]() of Questions (1.5) - (1.7) satisfies
of Questions (1.5) - (1.7) satisfies
![]() (2.8)
(2.8)
Proof. We multiply ![]() with both sides of Equation (1.5) and obtain
with both sides of Equation (1.5) and obtain
![]() (2.9)
(2.9)
Here
![]()
![]()
By using the Sobolev inequality
![]()
So
![]()
![]()
By the Young inequality, we obtain
![]()
From the (2.9), we obtain
![]()
So we have
![]()
3. Global Attractor and Dimension Estimation
Theorem 1. Assume that ![]() and
and ![]() so Questions (1.5) - (1.7) exist a unique smooth so-
so Questions (1.5) - (1.7) exist a unique smooth so-
lution ![]() and
and ![]()
Proof. By the method of Galerkin and Lemma 1-Lemma 3, we can easily obtain the existence of solutions. Next, we prove the uniqueness of solutions in detail.
Amusse ![]() are two solutions of Questions (1.5) - (1.7), so the difference of them
are two solutions of Questions (1.5) - (1.7), so the difference of them ![]() satisfies
satisfies
![]()
![]()
and
![]()
The two above formulae subtract and obtain
![]() (3.1)
(3.1)
We multiply ![]() with both sides of Equation (3.1) and obtain
with both sides of Equation (3.1) and obtain
![]() (3.2)
(3.2)
Here
![]()
Since the assume of Lemma 1, we obtain
![]()
![]()
From the (3.2) we can obtain
![]()
According to the Gronwall inequality,we obtain
![]()
So we can get ![]() the uniqueness is proved.
the uniqueness is proved.
Theorem 2. ![]() Let
Let ![]() be a Banach space, and
be a Banach space, and ![]() are the semigroup operators on
are the semigroup operators on![]() .
. ![]() here
here ![]() is a unit operator. Set
is a unit operator. Set ![]() satisfy the follow conditions
satisfy the follow conditions
1) ![]() is bounded. Namely
is bounded. Namely![]() , it exists a constant
, it exists a constant![]() , so that
, so that
![]() ;
;
2) It exists a bounded absorbing set ![]() namely
namely ![]() it exists a constant
it exists a constant ![]() so that
so that
![]() ;
;
3) When ![]()
![]() is a completely continuous operator
is a completely continuous operator![]() .
.
Therefor, the semigroup operators ![]() exist a compact global attractor.
exist a compact global attractor.
Theorem 3. Under the assume of Theorem 1, Questions (1.5) - (1.7) have global attractor
![]()
![]() is the bounded absorbing set of
is the bounded absorbing set of ![]() and satisfies
and satisfies
1) ![]()
2) ![]() here
here ![]() and it is a bounded set,
and it is a bounded set,
![]()
Proof. Under the conditions of Lemma 1 - Lemma 4, it exists the solution semigroup ![]() of Questions (1.5)- (1.7),
of Questions (1.5)- (1.7), ![]()
From Lemma 1 - Lemma 3, to ![]() is a bounded set that includes in the ball
is a bounded set that includes in the ball ![]()
![]()
This shows ![]() is uniformly bounded in
is uniformly bounded in ![]()
Furthermore, when ![]() there is
there is ![]() therefore,
therefore,
![]()
is the bounded absorbing set of semigroup ![]()
From Lemma 4, there are![]() . Since
. Since ![]() is tightly em-
is tightly em-
bedded, which means that the bounded set in ![]() is the tight set in
is the tight set in![]() , the semigroup operator
, the semigroup operator ![]() to
to ![]() is completely continuous. Furthermore we can know, the attractor A is
is completely continuous. Furthermore we can know, the attractor A is
w-limited set of the absorptive set ![]()
![]()
In order to estimate the Hausdorff and fractal dimension of the global attractor A of Questions (1.5) - (1.7), let Questions (1.5) - (1.7) linearize, then we obtain
![]()
![]() (3.3)
(3.3)
![]() (3.4)
(3.4)
where
![]()
So the solutions of Questions (1.5) - (1.7) are fully smooth. It is easy to prove the initial value, appropriate, smooth and linear Questions (3.3) - (3.4) have global and smooth solutions. Let
![]()
![]() and
and ![]() are constants, so it exists a constant
are constants, so it exists a constant ![]() and
and ![]() so there is
so there is ![]()
This suggests that ![]() is Frechet differential in
is Frechet differential in ![]()
Let ![]() be the solutions of the linear Equation (3.3) corresponding to the initial value
be the solutions of the linear Equation (3.3) corresponding to the initial value ![]() so there is
so there is
![]() (3.5)
(3.5)
![]() is linear mapping that is defined in the (3.4);
is linear mapping that is defined in the (3.4); ![]() represents the outer product;
represents the outer product; ![]() represents the trace;
represents the trace; ![]() is the orthogonal projection from
is the orthogonal projection from ![]() to the span
to the span ![]() So from (3.5), we can turn
So from (3.5), we can turn ![]() dimensions volume element
dimensions volume element ![]() into
into
![]()
![]() is secondly exponential, namely
is secondly exponential, namely
![]()
So
![]()
Here
![]()
Theorem 4. Under the assume of Theorem 3, the global attractor ![]() of Questions (1.5) - (1.7) has finite Hausdorff and fractal dimensin, and
of Questions (1.5) - (1.7) has finite Hausdorff and fractal dimensin, and
![]()
Here ![]() is a minimal positive integer of the following inequality
is a minimal positive integer of the following inequality
![]()
Proof. By theorem [8] , we need to estimate the lower bound of ![]() Let
Let ![]() be the orthogonal basis of subspace of
be the orthogonal basis of subspace of ![]()
![]()
Here
![]()
![]()
Under the bounded condition, ![]() is the standard eigenfunction of
is the standard eigenfunction of ![]() and the corresponding eigenvalues are
and the corresponding eigenvalues are ![]() and
and
![]()
Therefore, we can get
![]()
By ![]() and
and
![]()
we have
![]()
Therefore
![]()
Funding
This work is supported by the National Natural Sciences Foundation of People’s Republic of China under Grant 11161057.