The Connection between the Basel Problem and a Special Integral ()
1. Introduction
Basel problem asks for the precise value of the progression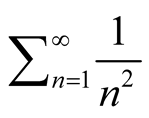 . It was first posed by Pietro Mengoli in 1644 and solved by Leonhard Euler in 1735 [1] . The value is known as
. It was first posed by Pietro Mengoli in 1644 and solved by Leonhard Euler in 1735 [1] . The value is known as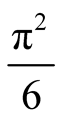 .
.
There are more general results [2] about the progression,
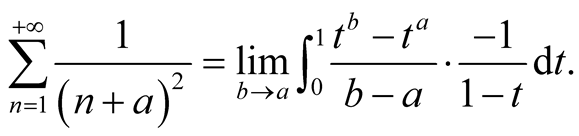
Let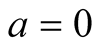 , it becomes the
, it becomes the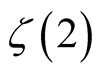 .
.
Moreover, using Fourier expansion of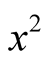 ,
,
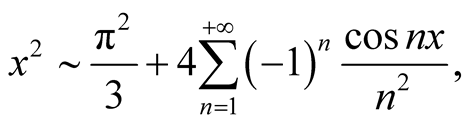
we will get
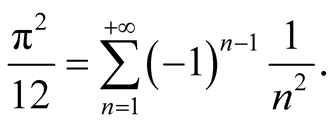 (1.1)
(1.1)
In the end of Section 5, we give another proof of (1.1) by using the relationship of two special integrals which are introduced in Sections 3 and 4. Also, inspired by this, in Section 6, we discuss about Bernoulli numbers and Genocchi numbers. We obtain some properties of Bernoulli numbers and Bernoulli polynomials.
2. Basic Properties
The convergence of the infinite series 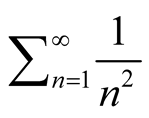 is obvious. We can use various methods to prove it. Especially, when we consider Riemann-Zeta function,
is obvious. We can use various methods to prove it. Especially, when we consider Riemann-Zeta function, 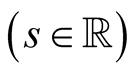
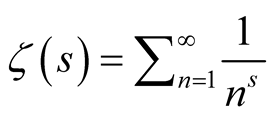 , the progression diverges when
, the progression diverges when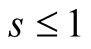 and converges when
and converges when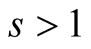 . Also, we can use the estimate of the partial sum of the series.
. Also, we can use the estimate of the partial sum of the series.

when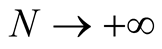 . Or we can use the Cauchy principle. In fact, for
. Or we can use the Cauchy principle. In fact, for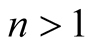 ,
,
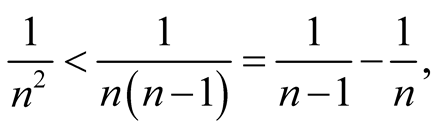
thus
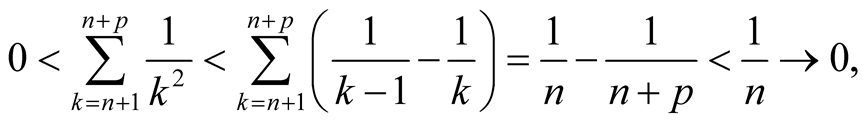
when . Then, the progression converges.
. Then, the progression converges.
3. Calculation of 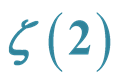
There are various proofs of the Basel problem and Robin Chapman wrote a survey [3] about these. Some are elementary and some will use advanced mathematics such as Fourier analysis, complex analysis or multivariable calculus. Here we review the method of Jiaqiang Mei [4] , which is rather elementary and easy to understand. There is also an elementary proof on the Wiki [1] .
Repeated use of the equation
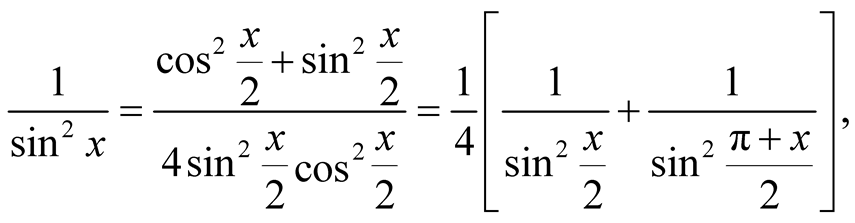
we get
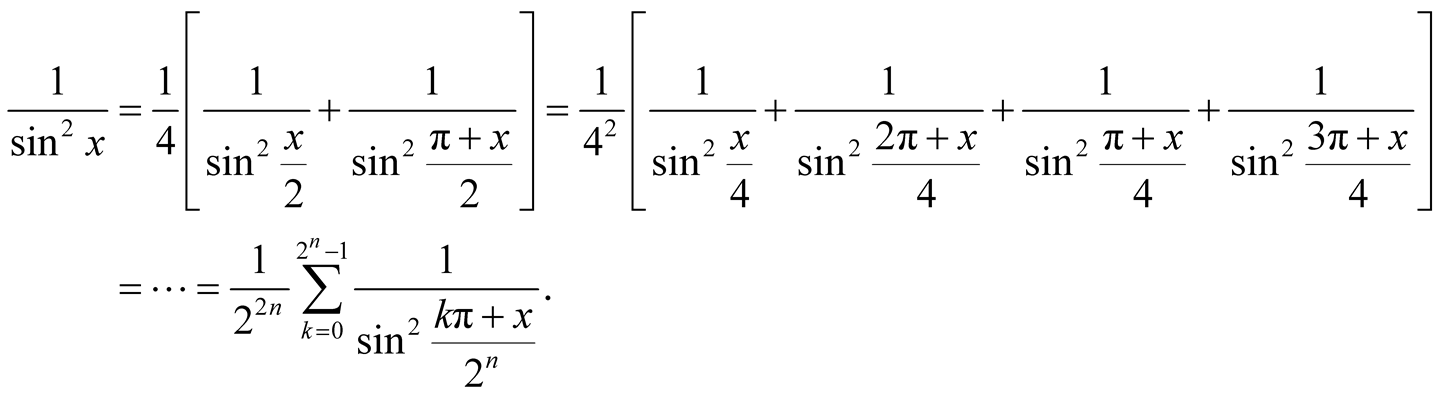 (1.2)
(1.2)
Note that
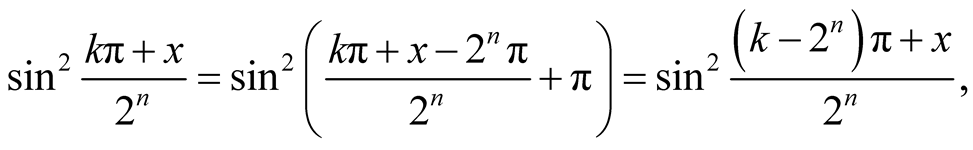
we may rewrite the Equation (1.2) as
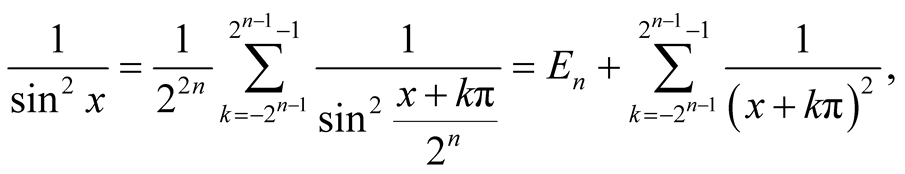
where
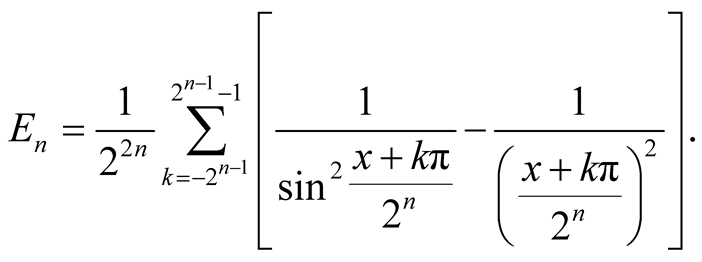
Using the inequality
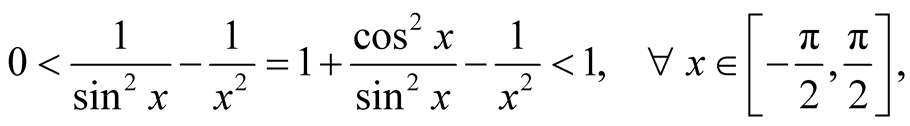
we get the estimation
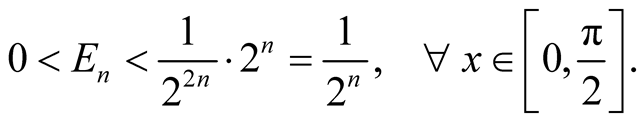
Let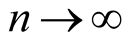 , we obtain the following equation
, we obtain the following equation

The above progression is uniformly convergent in any closed interval not containing 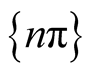 and can be written as
and can be written as

Especially, we have
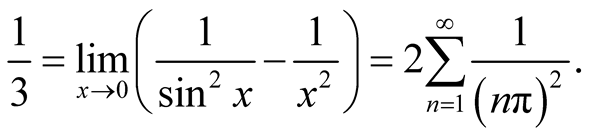
Therefore,
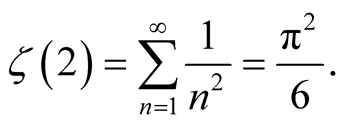
4. As a Special Case of Power Series
For the power series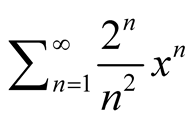 , we calculate the domain of convergence. Since
, we calculate the domain of convergence. Since
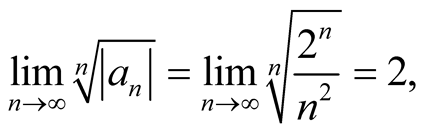
the radius of convergence equals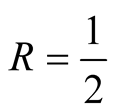 . If
. If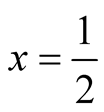 , the power series becomes the progression
, the power series becomes the progression 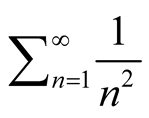 which is convergent. If
which is convergent. If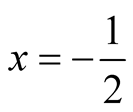 , then the power series becomes
, then the power series becomes 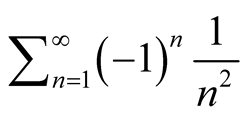 which is also convergent. Therefore, the domain of convergence is
which is also convergent. Therefore, the domain of convergence is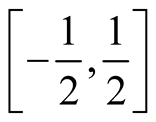 .
.
Suppose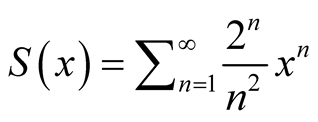 . We can do the derivation item by item in the inteval
. We can do the derivation item by item in the inteval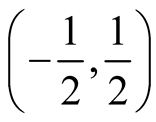 . That is,
. That is,
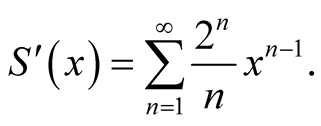
Multiply both sides by ,
,

Derivate both sides again, we get
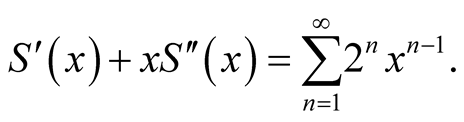
Thus,
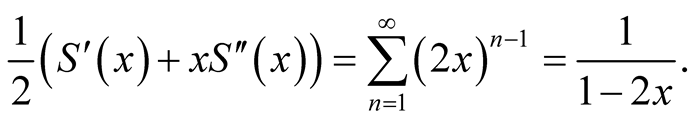
We obtain a second order ordinary differential equation
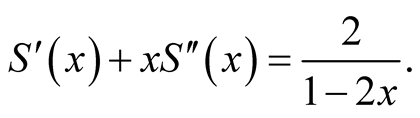 (1.3)
(1.3)
If we set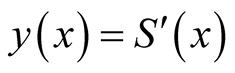 , the Equation (1.3) is converted to a first order equation,
, the Equation (1.3) is converted to a first order equation,
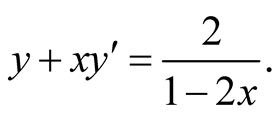
Multiplie both side by ,
,
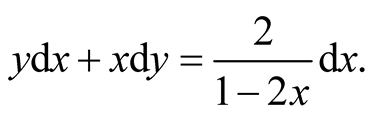
Let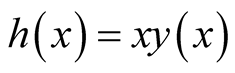 , we have
, we have
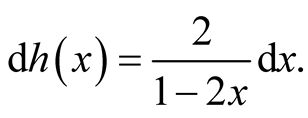
Then
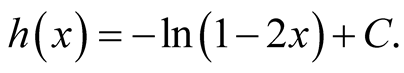
Using the initial conditions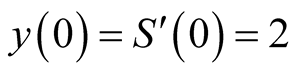 ,
, 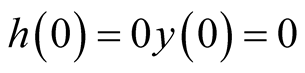 , we have
, we have
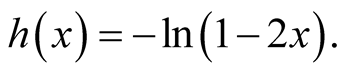
Then, if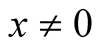 ,
,
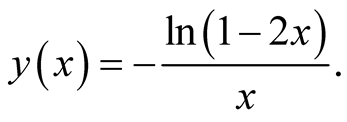
That is
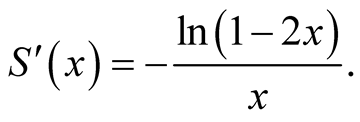
Note that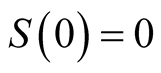 . Then,
. Then,
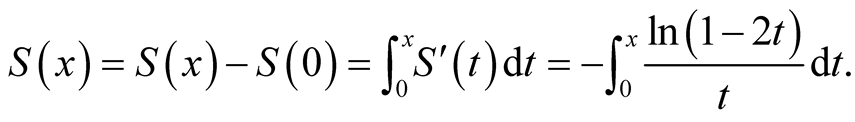
Particularly,
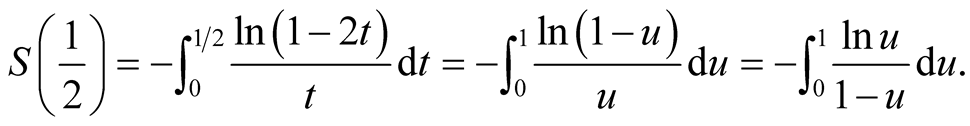
Therefore, for the improper integral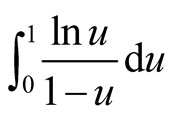 , we know its value is equal to
, we know its value is equal to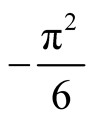 .
.
5. From the Special Integral to the Basel Problem
In this section, we will calculate the special integral arised in the last section, i.e.

For ,
,
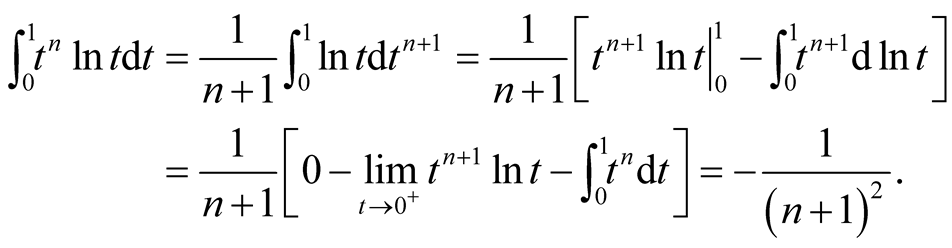
Thus
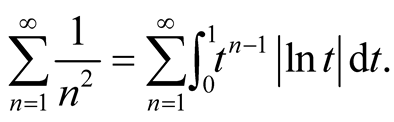
Let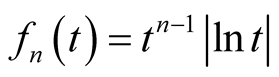 ,
, 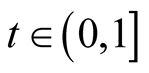 ,
,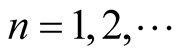 . Obviously,
. Obviously, 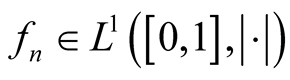 , where
, where 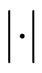 is Lebesgue measure.
is Lebesgue measure.
For simplicity, we denote 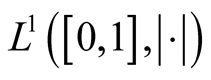 by
by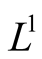 .
.
By Minkowski inequality [5] , we have
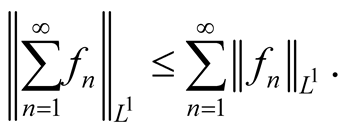 (1.4)
(1.4)
Then,
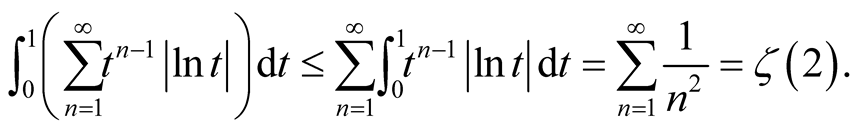
We will prove the equality holds in our case. First we have the following lemma.
Lemma 1. 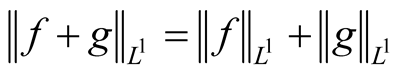 if and only if there is a real valued function h that is nonnegative a.e. such that when both f and g are not 0 then
if and only if there is a real valued function h that is nonnegative a.e. such that when both f and g are not 0 then 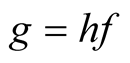 a.e.
a.e.
Proof. Please refer to [6] .
Lemma 1 can be generalized to infinite summation case.
Lemma 2. 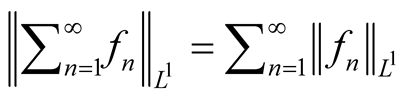 if and only if there is a real valued function f and a series of real valued functions
if and only if there is a real valued function f and a series of real valued functions 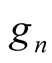 which have the same signs such that
which have the same signs such that 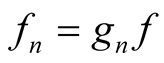 a.e.
a.e.
Proof. First, by induction, the lemma holds for finite sum. That is
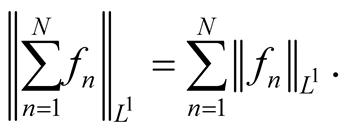
Let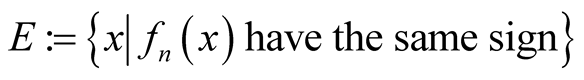 . Then,
. Then,
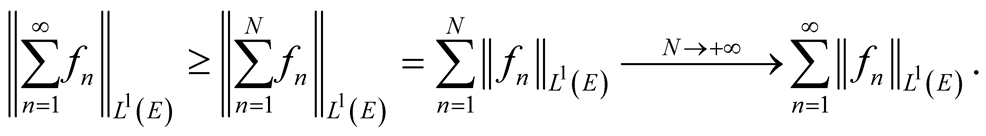
Since the measure of 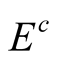 is zero, we have
is zero, we have
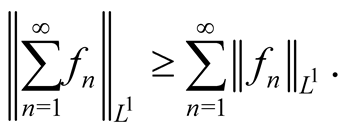
Combine Equation (1.4), we complete the proof.
On the other hand, we observe that, for 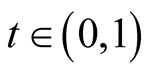
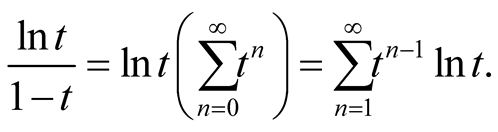
Then we get
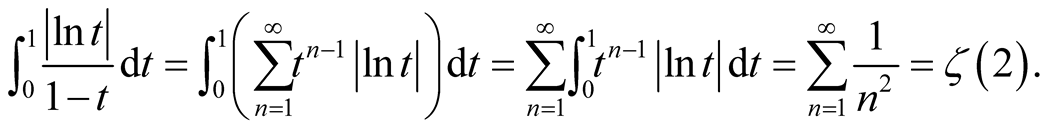
We give a remark about the second equality of the above equation. It can be infered by Fubini theorem or Tonelli’s theorem [7] .
Infact,
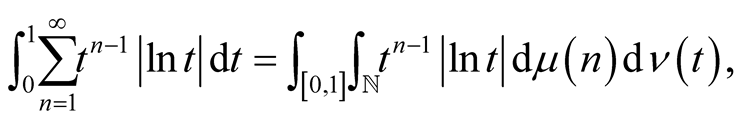
where 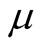 is the counting measure on
is the counting measure on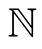 , and
, and 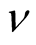 is the Lebesgue measure on
is the Lebesgue measure on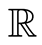 . Obviously, they are both
. Obviously, they are both 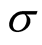 -finite measures. And since
-finite measures. And since 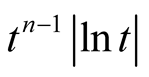 is non-negative, by Tonelli’s theorem,
is non-negative, by Tonelli’s theorem,
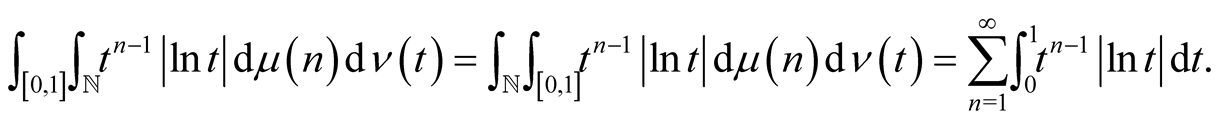
There are other ways to get this relationship from this special integral to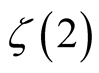 . First, recall the lemma established by James P. Lesko and Wendy D. Smith [2] .
. First, recall the lemma established by James P. Lesko and Wendy D. Smith [2] .
Lemma 3. For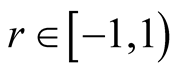 ,
, 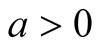 and
and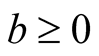 , we have
, we have
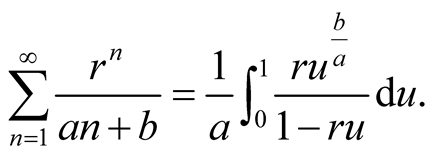 (1.5)
(1.5)
Especially, when 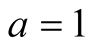 and
and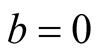 , (1.5) yields
, (1.5) yields

By this lemma,
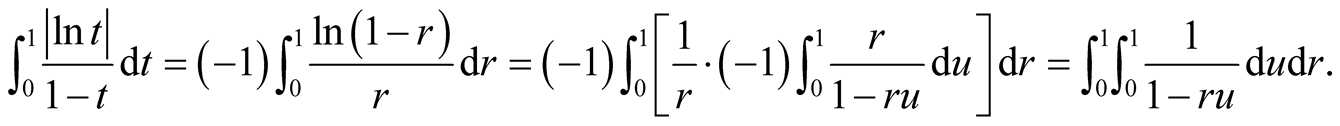
Then by monotone convergence theorem, it equals to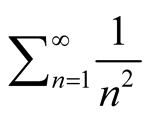 . See [3] .
. See [3] .
Or, we can do it in this way,
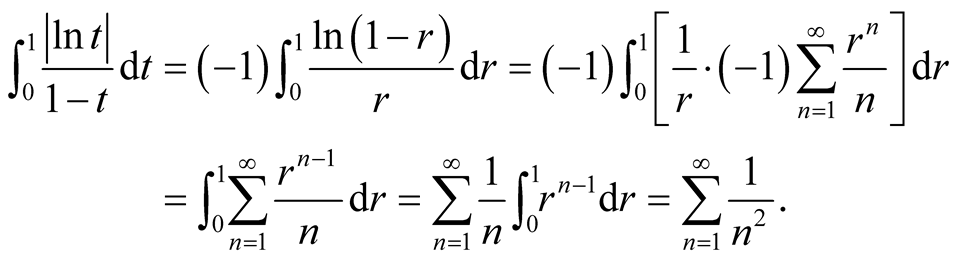
6. Relationship between Two Special Integrals
We will use a result from ([8] , Exer 20).
Lemma 4. Assume that the function 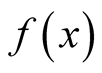 is monotone on the interval
is monotone on the interval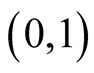 . It need not be bounded at the points
. It need not be bounded at the points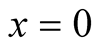 ,
,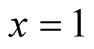 ; we assume however that the improper integral
; we assume however that the improper integral 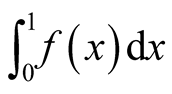 exists. Under these conditions,
exists. Under these conditions,
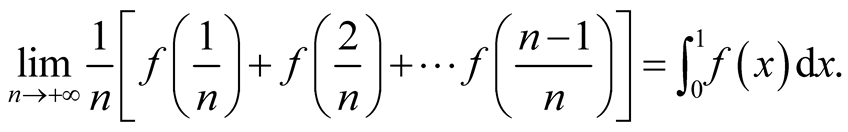
Then for our case, the integral 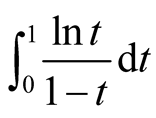 exists and satisfies the conditions. In fact, let
exists and satisfies the conditions. In fact, let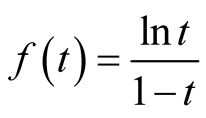 ,
, 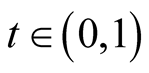 then
then
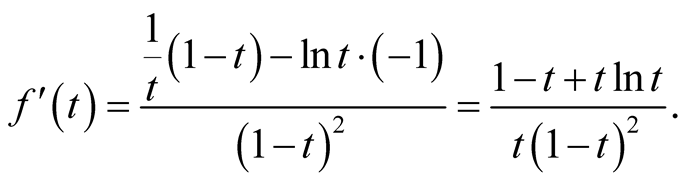
Let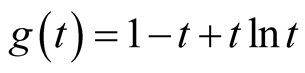 , then
, then
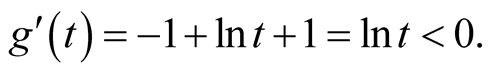
Since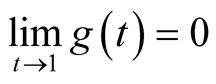 , we have
, we have 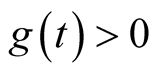 for
for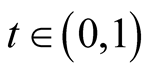 . So
. So 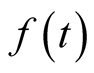 is monotone on the interval
is monotone on the interval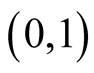 . Then by Lemma 4, we have
. Then by Lemma 4, we have
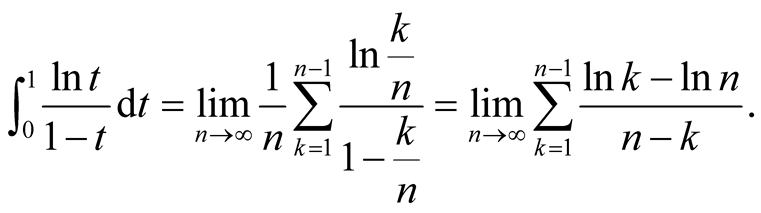
If we consider the improper integral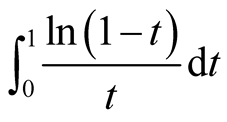 . Let
. Let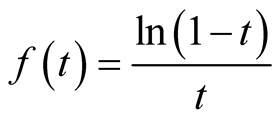 ,
,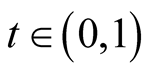 . Then
. Then
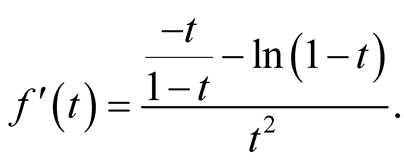
Let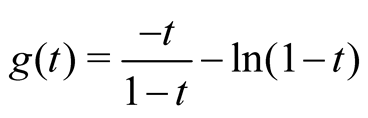 , then
, then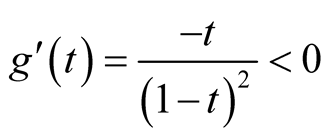 . Since
. Since
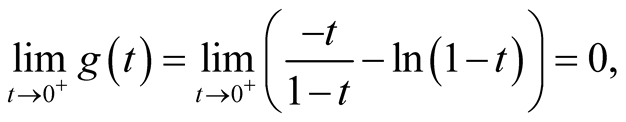
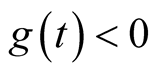 . Thus,
. Thus,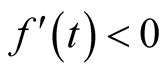 . So
. So 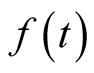 is also monotone on the interval
is also monotone on the interval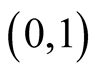 . By Lemma 4, we have
. By Lemma 4, we have

Next, we deduce the following equation and give another discription of (1.1),
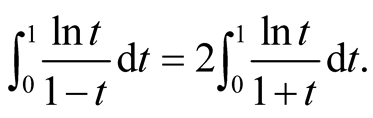 (1.6)
(1.6)
Lemma 5. Let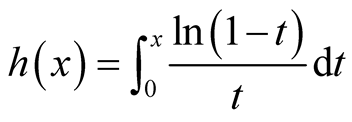 ,
, 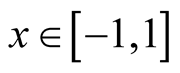 , then
, then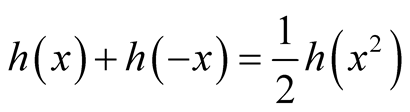 .
.
Proof. Let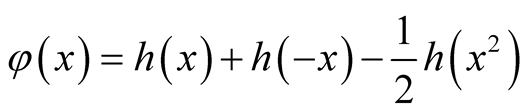 , it is easy to note that its derivate
, it is easy to note that its derivate 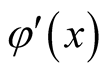 equals to zero and
equals to zero and
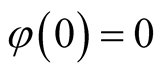 .
.
By changing variables,
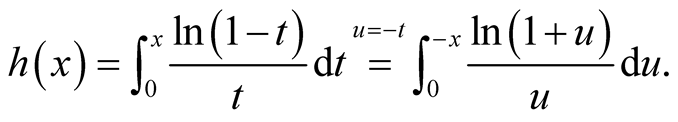
Then
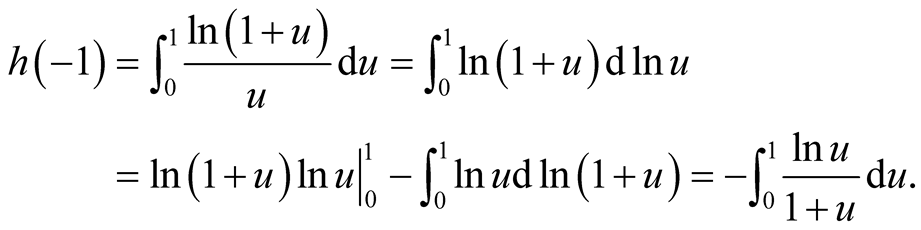
Here, note that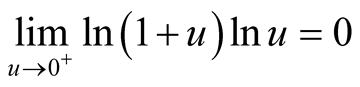 . By Lemma 5,
. By Lemma 5,
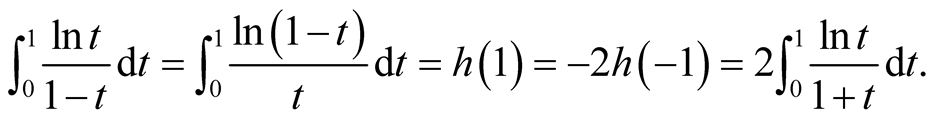
For the integral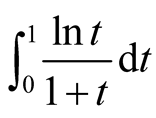 , we have a relevant result.
, we have a relevant result.
Lemma 6. Let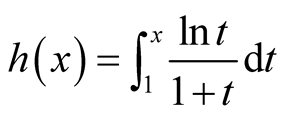 ,
, 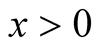 , then
, then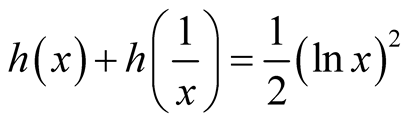 .
.
Proof.

then,
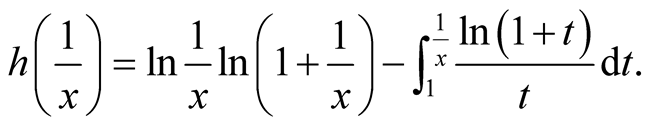
Hence,
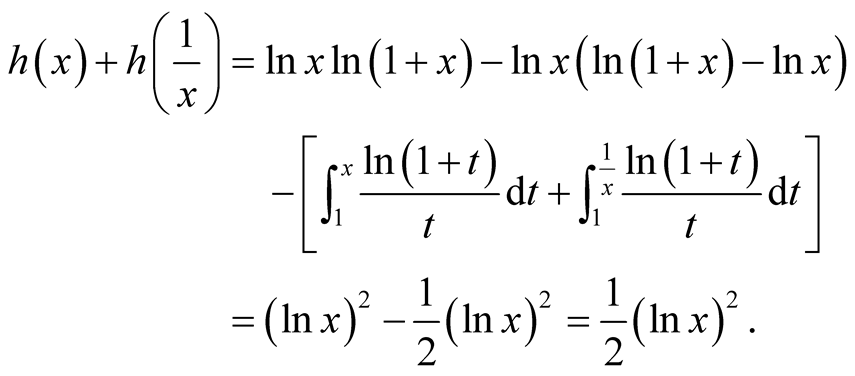
The second equality holds, because
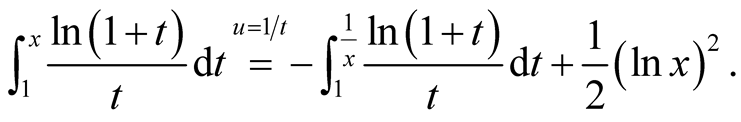
Observe that
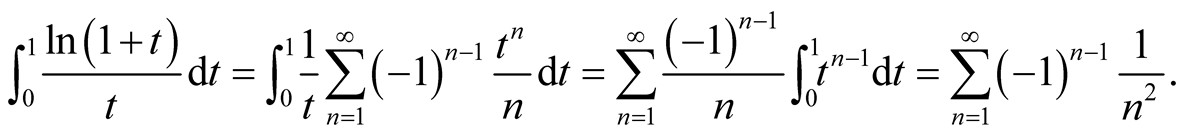
Thus
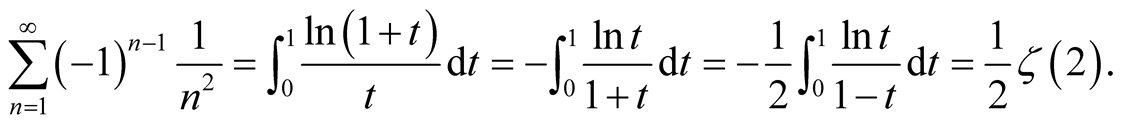
Applying the same argument in beginning of this section, we get
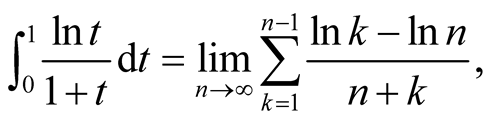
and
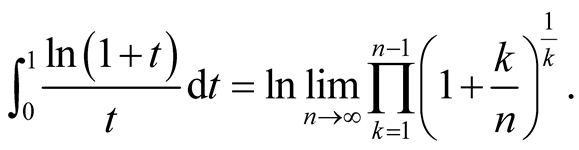
Remark. It must be very interesting if we could calculate the integral 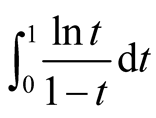 not using the progression
not using the progression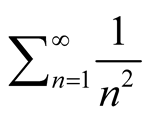 .
.
Remark. Similarly, we can prove that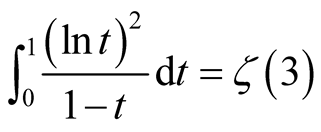 .
.
7. Bernoulli Numbers and Bernoulli Polynomials
Recall some facts of Bernoulli numbers, and for more information, please refer to [4] [9] -[12] .
The Bernoulli numbers 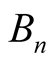 are defined by the power series expansion
are defined by the power series expansion
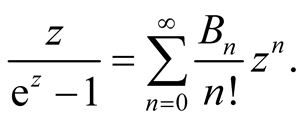
Then
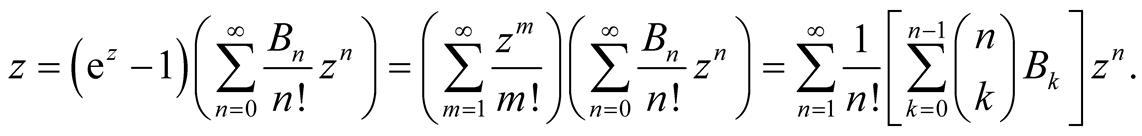
Thus we get a recursion formula for the Bernoulli numbers, namely
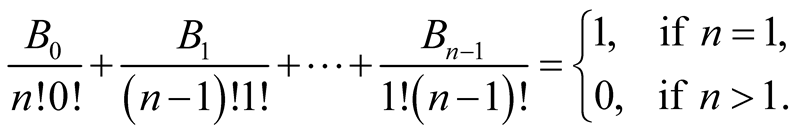
We get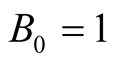 . From the identity
. From the identity
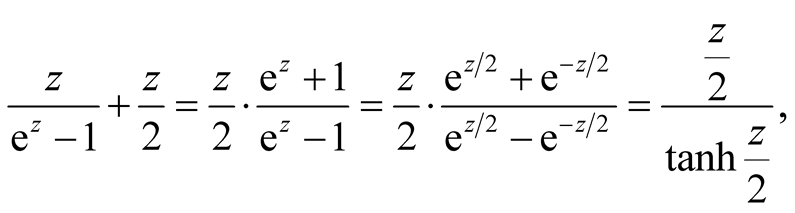
the function 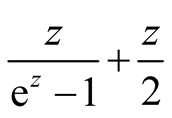 is an even function. Hence it has only even terms in its power series expansion.
is an even function. Hence it has only even terms in its power series expansion.
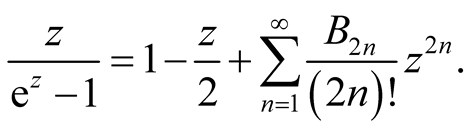
Sometimes, people prefer to use 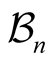 to denote
to denote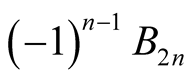 , then
, then
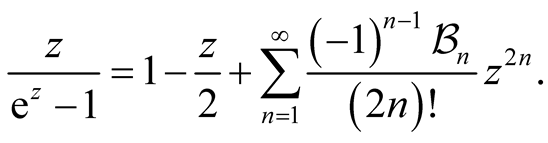
We have various ways to get the important equation.
Lemma 7.
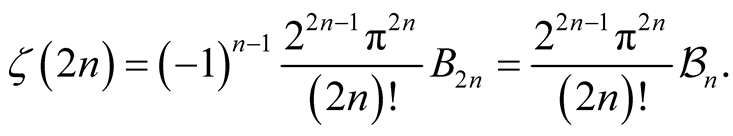
Proof. By replacing 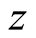 by
by 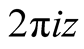 in the identity
in the identity
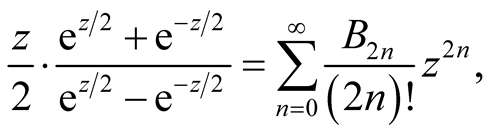
we get
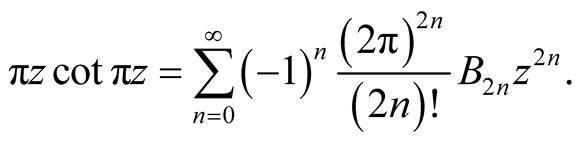
Then by taking the logarithmic derivative of the product expansion for the sine,

we get the expansion of .
.
Comparing the coefficents of , we get (7).
, we get (7).
Another way is to take the logarithmic derivative of the identity [4]
which yields

Then we get (7) by comparing with
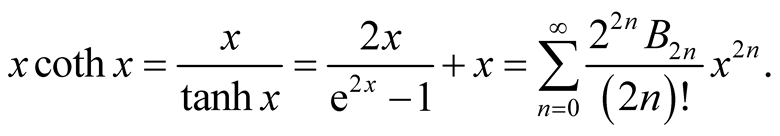
Proposition 1.
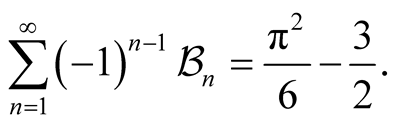
Proof.

where
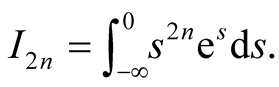
It is easy to prove that 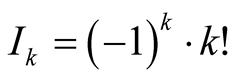 by induction. Therefore,
by induction. Therefore,
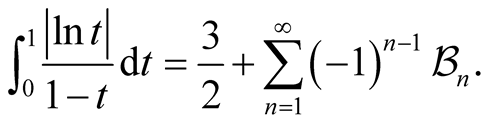
Let us consider the expansion
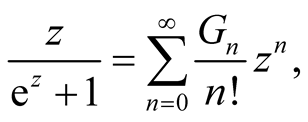
where 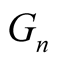 are Genocchi numbers. Then
are Genocchi numbers. Then
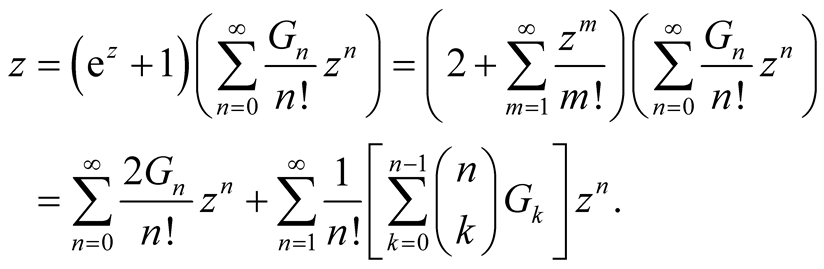
Thus, 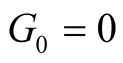 and
and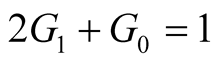 , which infers that
, which infers that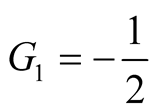 . For
. For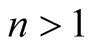 ,
,
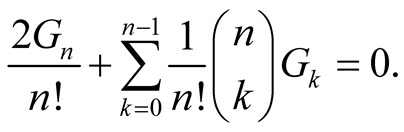
That is,
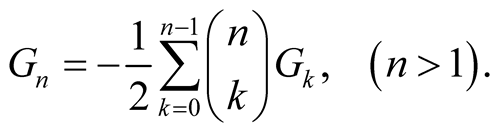 (1.7)
(1.7)
Note that
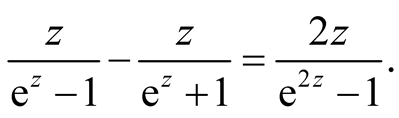
Taking expansion,
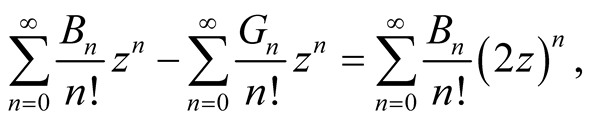
we have
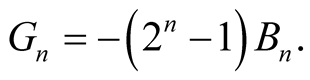 (1.8)
(1.8)
This give a quick way to compute Bernoulli numbers since in (1.7) we have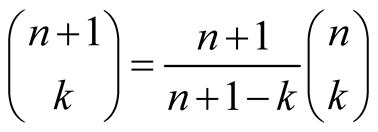 .
.
If let 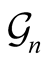 denote
denote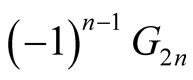 , then
, then
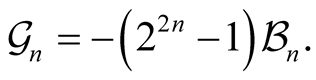
Proposition 2.
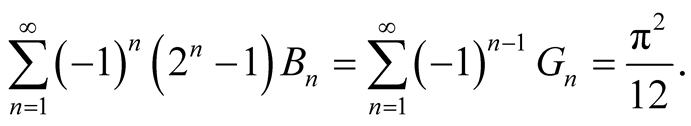
Proof. By changing variables,
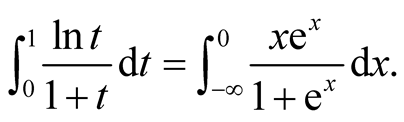
Note that
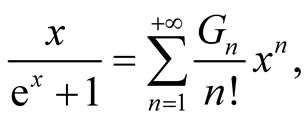
then
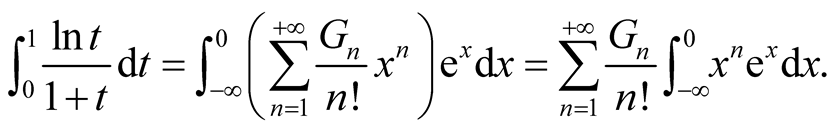
Set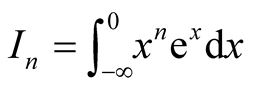 , then
, then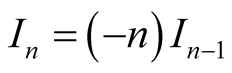 . By induction, we prove that
. By induction, we prove that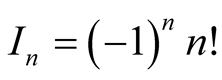 . Therefore,
. Therefore,
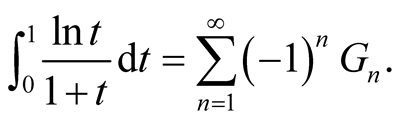
Together with (1.6), we have
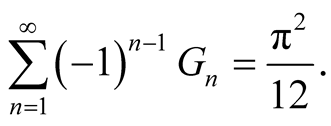
Remark. Since 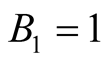 and
and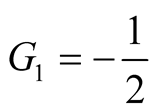 , the proposition can also be written as
, the proposition can also be written as
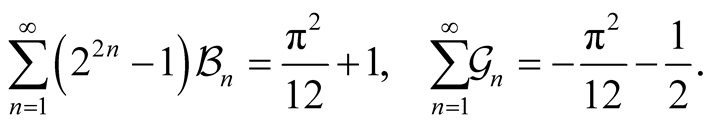
Bernoulli polynomials 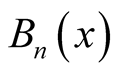 are defined by the formula
are defined by the formula
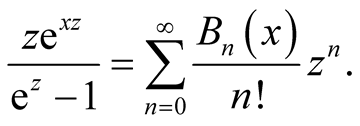
The functions 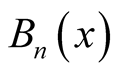 are polynomials in
are polynomials in 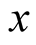 and
and
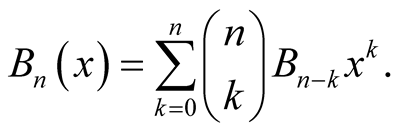
Similarly, we define 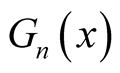 by the formula
by the formula
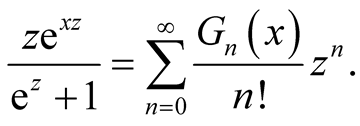 (1.9)
(1.9)
The functions 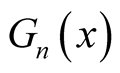 are polynomials in
are polynomials in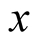 . In fact,
. In fact,
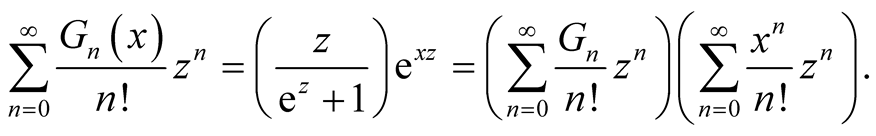
Comparing the coefficients of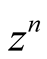 , we have
, we have
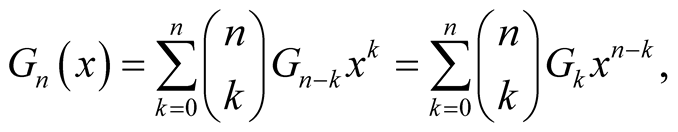 (1.10)
(1.10)
and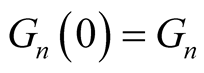 . Using (1.7), for
. Using (1.7), for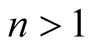 , we have
, we have
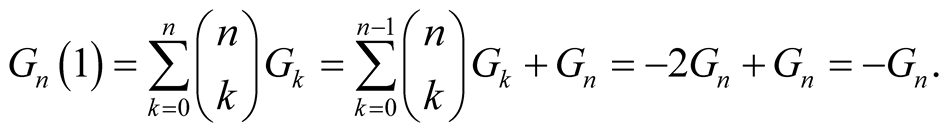
On the other hand, by definition,
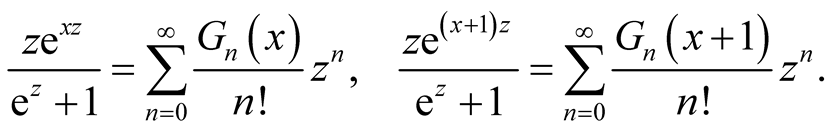
Do the addition,
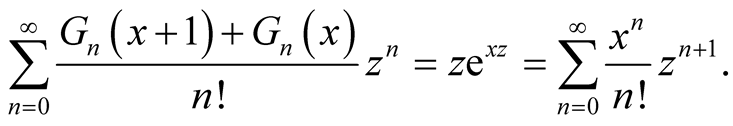
Comparing the coefficients of , we have
, we have
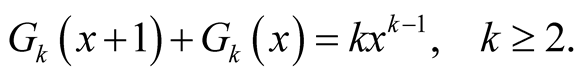
Let 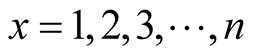 and summation these equations, we get
and summation these equations, we get
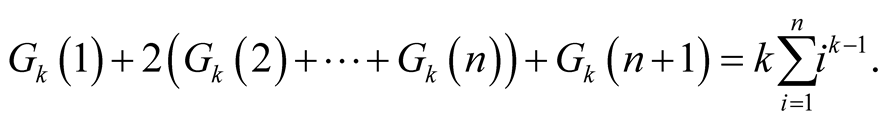
From the equation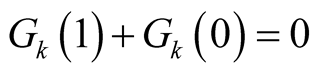 , we infer that
, we infer that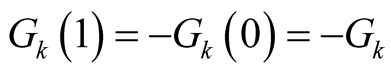 .
.
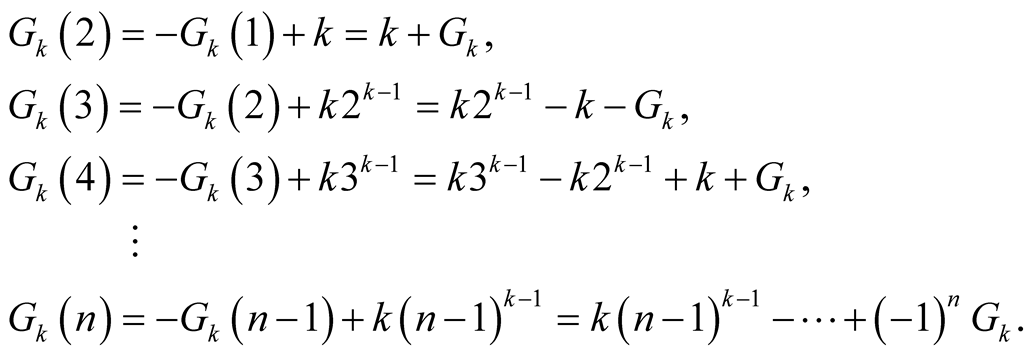
Therefore,
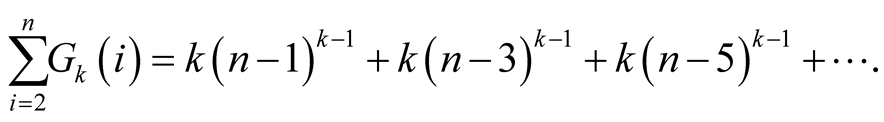
If ,
,
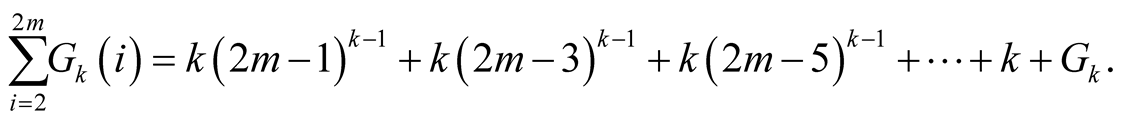
If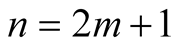 ,
,
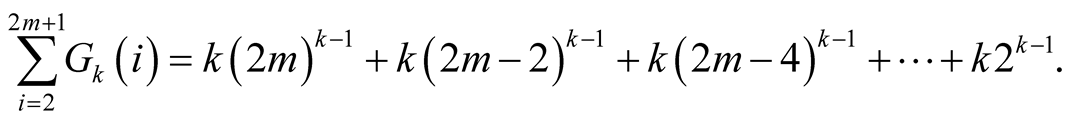
Whether  is odd or even, we always have the following trivial identity.
is odd or even, we always have the following trivial identity.
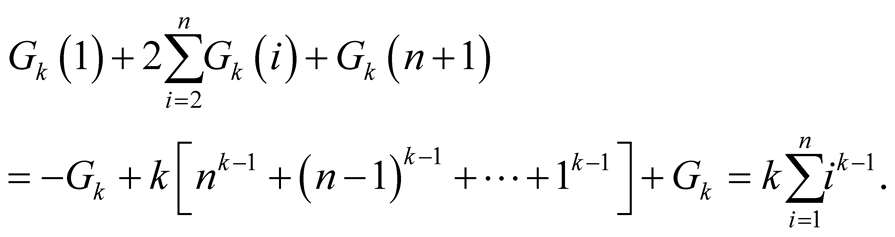
By differentiating on 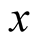 at both sides of (1.9), we also have
at both sides of (1.9), we also have
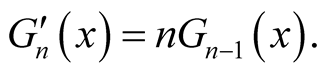
But being different from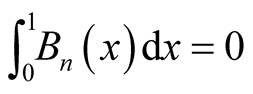 , we have
, we have
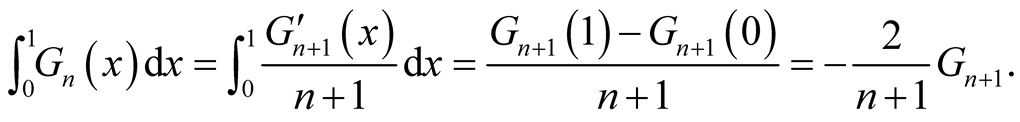
Proposition 3. i)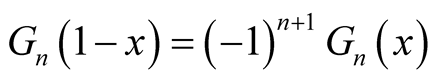 .
.
ii)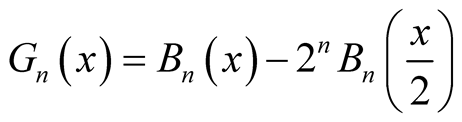 .
.
iii)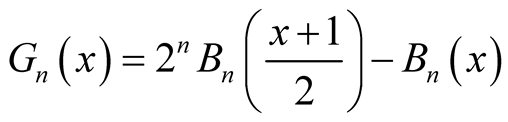 .
.
iv)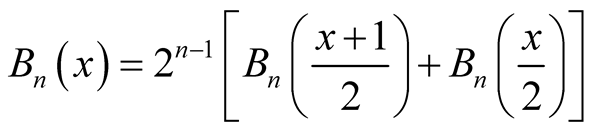 .
.
Proof. i)

thus,
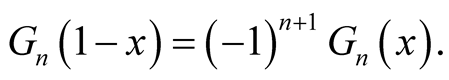
ii)
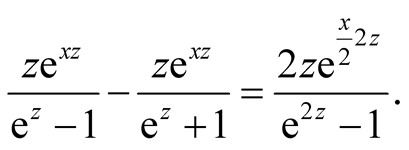
By comparing the coeffients of , we get
, we get
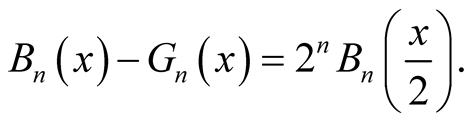
iii)

By comparing the coeffients of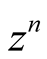 , we get
, we get
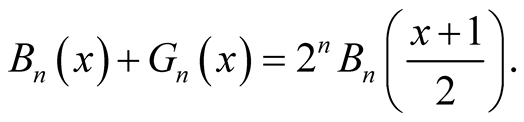
iv) by ii) and iii).
Remark. 1) Especially, we have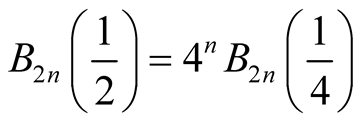 , since
, since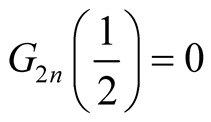 .
.
2) Let 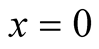 or 1 in iv), we have
or 1 in iv), we have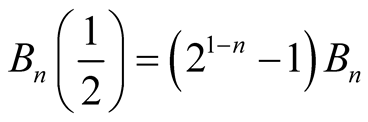 . Thus,
. Thus,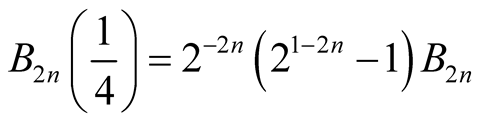 .
.
3) Let  in iii), we will get
in iii), we will get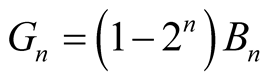 .
.
Equation (1.8) can also be deduced in the following way. Using
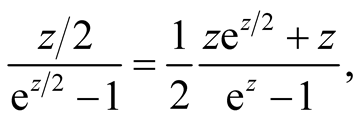
we obtain
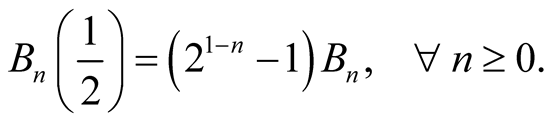 (1.11)
(1.11)
Similarly,
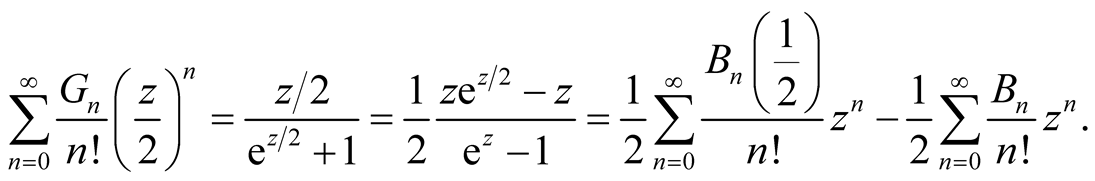
This infers that
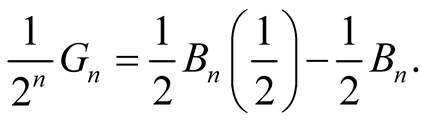
By substituting (1.11) in the above formula, we obtainde
Acknowledgements
We express our gratitude to David Harvey who point out that the numbers 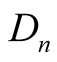 in our manuscript (here is
in our manuscript (here is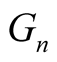 ) are essentially the Genocchi numbers, see [13] .
) are essentially the Genocchi numbers, see [13] .
The work is partially supported by National Natural Science Foundation of China (NSFC), Tianyuan fund for Mathematics, No. 11126046, and the University Science Research Project of Jiangsu Province (13KJB110029).