1. Introduction
The Riemann-zeta function is the analytic extension of
 (1)
(1)
where Euler’s identity on the right hand side expresses the relation of the integers to the primes. The zeros  of Riemann’s analytic continuation of (1) comprise the negative even integers,
of Riemann’s analytic continuation of (1) comprise the negative even integers, , and an infinite number of nontrivial zeros
, and an infinite number of nontrivial zeros 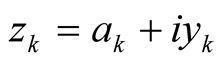 in the strip
in the strip .
.
A general approach to find zeros is by continuation[1] . If  is a starting point of a path
is a starting point of a path  with tangent
with tangent ,
,
 (2)
(2)
then the endpoint  is a zero of
is a zero of , all of which are isolated. All known nontrivial zeros satisfy
, all of which are isolated. All known nontrivial zeros satisfy to within numerical precision, the first three of which are
to within numerical precision, the first three of which are ,
,

 By the symmetry
By the symmetry
 (3)
(3)
it suffices to study zeros in the half plane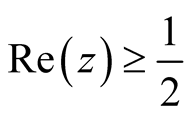 . Figure 1illustrates root finding by (2) for the first few zeros.
. Figure 1illustrates root finding by (2) for the first few zeros.
Continuation (2) is determined by the prime numbers, since
 (4)
(4)
whereby
 (5)
(5)
The poles of  at the zeros are therefore expressed by the prime number distribution.
at the zeros are therefore expressed by the prime number distribution.
In this paper, we study the distribution of zeros  by Fourier analysis of the function
by Fourier analysis of the function
 (6)
(6)
on , where
, where
 (7)
(7)
with summation over all primes. In what follows, we put
 (8)
(8)
The  are absolutely summable by Stirling’s formula and the asymptotic distribution of
are absolutely summable by Stirling’s formula and the asymptotic distribution of .
.
Theorem 1.1. In the limit as  becomes small, we have the asymptotic behavior
becomes small, we have the asymptotic behavior
 (9)
(9)
In (9), is evidently unbounded in the limit as
is evidently unbounded in the limit as  approaches zero whenever a finite number of zeros
approaches zero whenever a finite number of zeros 
exists off the critical line .
.
Corollary 1.2. If  is bounded, then the Riemann hypothesis is true or there are infinitely many zeros
is bounded, then the Riemann hypothesis is true or there are infinitely many zeros
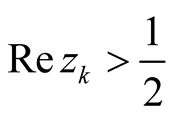 .
.
A similar relation between the distribution of  and the primes is [2] [3]
and the primes is [2] [3]
 (10)
(10)
based on the Chebyshev functions
 (11)
(11)
where the sum is over all primes  and integers
and integers . In (9),
. In (9), has a normalization by
has a normalization by  according to and
according to and  is absolutely convergent for all
is absolutely convergent for all , whereas in (10)
, whereas in (10)  is normalized by
is normalized by  and the sum
and the sum
 is not absolutely convergent. Similar to Corollary 1.2, the left hand side of (10) will be bounded in the limit of large
is not absolutely convergent. Similar to Corollary 1.2, the left hand side of (10) will be bounded in the limit of large  if the Riemann hypothesis is true.
if the Riemann hypothesis is true.
Section 2 presents some preliminaries on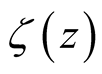 . Section 3 gives an integral representation of
. Section 3 gives an integral representation of  and a discussion on its singularity at
and a discussion on its singularity at . In Section 4, Cauchy’s integral formula is applied to derive a sum of residues associated with the
. In Section 4, Cauchy’s integral formula is applied to derive a sum of residues associated with the . The proof Theorem 1.1 follows from a Fourier transform and asymptotic analysis (Section 5). In Section 6, we illustrate a direct evaluation of
. The proof Theorem 1.1 follows from a Fourier transform and asymptotic analysis (Section 5). In Section 6, we illustrate a direct evaluation of  using the primes up to one trillion, showing harmonic behavior arising from
using the primes up to one trillion, showing harmonic behavior arising from  by the first few zeros
by the first few zeros . We summarize our findings in Section 7.
. We summarize our findings in Section 7.
2.Background
Our analysis begins with some known properties of  in, e.g.,[4] -[9] .
in, e.g.,[4] -[9] .
Riemann obtained an analytic extension of  by expressing
by expressing  in terms of
in terms of ,
,
 (12)
(12)
where
 (13)
(13)
Here, satisfies
satisfies  as
as  approaches zero by the identity
approaches zero by the identity 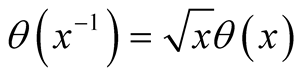 for the Jacobi function
for the Jacobi function  1. On
1. On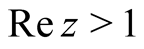 , it obtains the meromorphic expression (e.g. Borwein et al., 2006)
, it obtains the meromorphic expression (e.g. Borwein et al., 2006)
 (14)
(14)
which gives a maximal analytic continuation of  and shows a simple pole at
and shows a simple pole at  with residue 1.
with residue 1.
Riemann further introduced the symmetric form ,
, satisfying
satisfying
 , whereby
, whereby
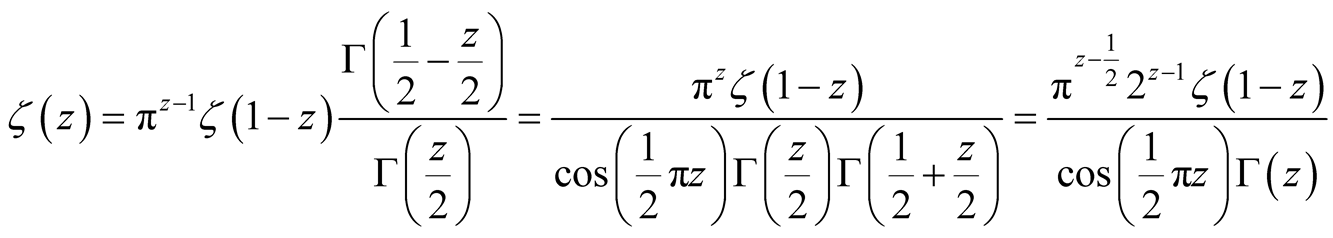 (15)
(15)
using  and
and . Along
. Along ,
, is nonvanishing [10] -[13] , allowing
is nonvanishing [10] -[13] , allowing
 (16)
(16)
in terms of the digamma function
 (17)
(17)
in the limit of large .
.
Lemma 2.1. In the limit of large , the logarithmic derivative of
, the logarithmic derivative of  satisfies
satisfies
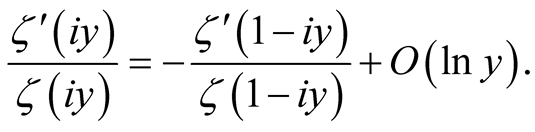 (18)
(18)
Proof. The result follows from (17) and (16). Lemma 2.2.Along the line , we have the asymptotic expansion
, we have the asymptotic expansion in the limit of large
in the limit of large , whereby the
, whereby the  are absolutely summable.
are absolutely summable.
Proof.Recall (8) and the asymptotic expansion  with a branch cut along the negative real axis. In the limit of large
with a branch cut along the negative real axis. In the limit of large ,
, , and hence
, and hence , since
, since  as
as 
becomes large. Hence,the  are absolutely summable. Numerically, their sum is small,
are absolutely summable. Numerically, their sum is small,
based on a large number of known zeros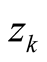 .Lemma 2.3. In the limit of large
.Lemma 2.3. In the limit of large , we have
, we have
 (19)
(19)
Proof. By Lemma 2.1-2.2, we have
 (20)
(20)
for large . Also[4] [14] [15]
. Also[4] [14] [15]
 (21)
(21)
on  for some positive constants
for some positive constants .,
.,
3.An IntegralRepresentation of 
Following the same steps leading to the Riemann integral for , we have
, we have
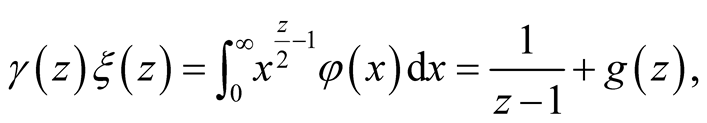 (22)
(22)
where  absorbs the simple pole in
absorbs the simple pole in  at
at  due to the simple pole in
due to the simple pole in  at
at , leaving
, leaving
 analytic at
analytic at . Following a decomposition
. Following a decomposition ,
,
 (23)
(23)
and substitution ,
, appears as the Laplace transforms
appears as the Laplace transforms
 (24)
(24)
These integral expressions allow continuations to , respectively, the entire complex plane.
, respectively, the entire complex plane.
Lemma 3.1. Analytic extension of  extends to
extends to .
.
Proof. With , the second term on the right hand side in (5) satisfies
, the second term on the right hand side in (5) satisfies
 (25)
(25)
which is bounded in . Since the second term
. Since the second term  in (5) is analytic in
in (5) is analytic in , it follows that
, it follows that  in is analytic on
in is analytic on . Following (5) as
. Following (5) as  approaches
approaches  from the right, we have
from the right, we have
 (26)
(26)
where  is analytic at
is analytic at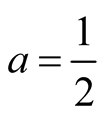 . By (22), as
. By (22), as  approaches
approaches  from the right, we have
from the right, we have
 (27)
(27)
where  is analytic about
is analytic about . Figure 2 shows a numerical evaluation of
. Figure 2 shows a numerical evaluation of  for small
for small  evaluated for the 37.6 billion primes up to one trillion, allowing
evaluated for the 37.6 billion primes up to one trillion, allowing  down to
down to 
 in view of the requirement for an accurate truncation in
in view of the requirement for an accurate truncation in  as defined by (7). The result shows asymptotic harmonic behavior in the limit as
as defined by (7). The result shows asymptotic harmonic behavior in the limit as  becomes small.
becomes small.
If the integral
 (28)
(28)
is absolutely convergent as  approaches zero, e.g., when
approaches zero, e.g., when  is of one sign in some neighborhood of
is of one sign in some neighborhood of
 , as in the numerical evaluation shown in Figure 2, then
, as in the numerical evaluation shown in Figure 2, then  has an analytic extension into
has an analytic extension into 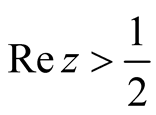
with no singularities, implying the absence of  in this region. However, this requires information on the point wise behavior of
in this region. However, this requires information on the point wise behavior of , which goes beyond the relatively weaker integrability property (23).
, which goes beyond the relatively weaker integrability property (23).
To make a step in this direction, we next apply a linear transform to (5) to derive the asymptotic behavior of 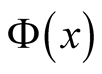 in terms of the distribution
in terms of the distribution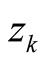 .
.
4.A Sum of Residues ZAssociated with the Non-Trivial Zeros
Consider
 (29)
(29)
and its Fourier transform
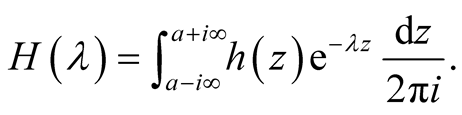 (30)
(30)
Lemma 4.1.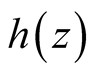 has a simple pole at
has a simple pole at  with residue 1 and simple poles at each of the nontrivial zeros
with residue 1 and simple poles at each of the nontrivial zeros  of
of  with residue
with residue .
.
Proof. We have (e.g. Borwein et al. 2006)
 (31)
(31)
where  is a constant, so that
is a constant, so that
 (32)
(32)
Here
 (33)
(33)
where  denotes the digamma function as before, includes contributions from the logarithmic derivative of the factor to
denotes the digamma function as before, includes contributions from the logarithmic derivative of the factor to 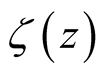 in (31), whose singularities are restricted to the trivial zeros of
in (31), whose singularities are restricted to the trivial zeros of . We now consider the Fourier integral over
. We now consider the Fourier integral over  as part of contour integration closed over
as part of contour integration closed over  and
and .
.
Proposition 4.2. The Fourier transform of  over
over  satisfies
satisfies
 (34)
(34)
in the limit of large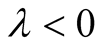 .
.
Proof. Integration over 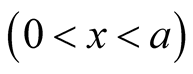
 gives
gives
 (35)
(35)
where we choose  to be between two consecutive values of
to be between two consecutive values of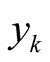 . We have
. We have
 (36)
(36)
In the limit as  approaches infinity,
approaches infinity, approaches zero and
approaches zero and  becomes small by Lemma 2.2., whence
becomes small by Lemma 2.2., whence
 (37)
(37)
Next, integration over  with a small semicircle around
with a small semicircle around  obtains an
obtains an  result in the limit of large
result in the limit of large  by application of Lemma 2.1-2.3 and the Riemann-Lebesgue Lemma. The result now follows in the limit as
by application of Lemma 2.1-2.3 and the Riemann-Lebesgue Lemma. The result now follows in the limit as  approaches infinity, taking into account the residue sum
approaches infinity, taking into account the residue sum  associated with the
associated with the  and absolute summability of the
and absolute summability of the . ,
. ,
5.Proof of Theorem 1.1
Multiplying (5) by , we have
, we have
 (38)
(38)
that is, by (22) and (29),
 (39)
(39)
We thus consider
 (40)
(40)
which ab initio is defined on 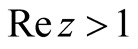 by Euler’s identity with Fourier transform
by Euler’s identity with Fourier transform
 (41)
(41)
Turning to the right hand side of (40), we consider the coefficients
 (42)
(42)
Here, since
since . In particular,
. In particular, and
and
 has a well defined limit and
has a well defined limit and  in the limit as
in the limit as  becomes arbitrarily large.
becomes arbitrarily large.
Lemma 5.1. The sum  is well-defined on
is well-defined on .
.
Proof. The result follows from the case . By the Prime Number Theorem,
. By the Prime Number Theorem, , whereby summation over the tails
, whereby summation over the tails  satisfy
satisfy
 (43)
(43)
whenever . Hence, for
. Hence, for ,
, whenever
whenever . It follows that
. It follows that
 (44)
(44)
on .Lemma 5.2.For any
.Lemma 5.2.For any , the Fourier transform of
, the Fourier transform of  over
over  satisfies
satisfies
 (45)
(45)
Proof. The Fourier integral can be obtained in a contour integration with closure over  and the edges
and the edges

 for large
for large . In the notation (42), it obtains a residue
. In the notation (42), it obtains a residue 
at , since
, since , whence
, whence
 (46)
(46)
The integral (46) exists by virtue of a removable singularity of  at
at . It asymptotically decays to zero for large
. It asymptotically decays to zero for large  when
when 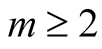 by the Riemann-Lebesgue Lemma. We now consider (40) with (22),
by the Riemann-Lebesgue Lemma. We now consider (40) with (22),
 (47)
(47)
with a remainder
 (48)
(48)
Lemma 5.3. For , the Fourier transform
, the Fourier transform
 (49)
(49)
in the limit of large .
.
Proof. Since  is analytic in
is analytic in , we are at liberty to consider the transform
, we are at liberty to consider the transform  on
on
 . The result follows from the Riemann-Lebesgue Lemma. Proof of Theorem 1.1. The Fourier transform of (47) is
. The result follows from the Riemann-Lebesgue Lemma. Proof of Theorem 1.1. The Fourier transform of (47) is
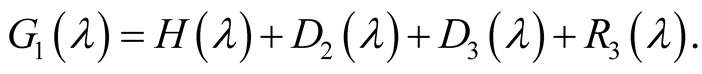 (50)
(50)
By Proposition 4.2 and Lemmas 5.1-5.2, we have
 (51)
(51)
With , Theorem 1.1 now follows. ,
, Theorem 1.1 now follows. ,
6.Numerical Illustration of Asymptotic Harmonic Behavior
The harmonic behavior emerges in
 (52)
(52)
To search for higher harmonics  associated with the zeros
associated with the zeros  in
in
 , we compare the spectrum of
, we compare the spectrum of  by taking a Fast Fourier Transform with respect to
by taking a Fast Fourier Transform with respect to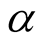 ,
,
 (53)
(53)
and compare the results with an analytic expression for the Fourier coefficients of the
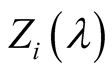 ,
,
 (54)
(54)
where  denotes the Bessel function of the first of order
denotes the Bessel function of the first of order . Figure 3 shows the first 21 harmonics in our evaluation of
. Figure 3 shows the first 21 harmonics in our evaluation of , which is about the maximum that can be calculated by direct summation in quad precision.
, which is about the maximum that can be calculated by direct summation in quad precision.
7.Conclusions
The zeros  of the Riemann-zeta function are endpoints of continuation, defined by an expressed by a regularized sum
of the Riemann-zeta function are endpoints of continuation, defined by an expressed by a regularized sum  over the prime numbers defined by (6).
over the prime numbers defined by (6).
The zeros  of
of  introduce asymptotic harmonic behavior in
introduce asymptotic harmonic behavior in 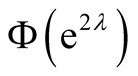 as a function of
as a function of defined by the sum
defined by the sum  of residues of the
of residues of the , shown in Figure 2,Figure 3. Primes up to 4 billion are needed to identify the first 4 harmonics, up to 70 billion for the 10 and up to 1 trillion for the first 21. It appears that, effectively, the prime number range scales exponentially with the number of harmonics it contains.
, shown in Figure 2,Figure 3. Primes up to 4 billion are needed to identify the first 4 harmonics, up to 70 billion for the 10 and up to 1 trillion for the first 21. It appears that, effectively, the prime number range scales exponentially with the number of harmonics it contains.
Theorem 1.1 describes a correlation between the distribution of the primes and the distribution of the nontrivial zeros . Suppose there are a finite number of zeros
. Suppose there are a finite number of zeros  in
in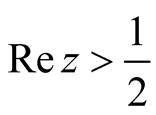 . We may then consider
. We may then consider  for which
for which  gives rise to dominant exponential growth in
gives rise to dominant exponential growth in  in the limit as
in the limit as  becomes large. This observation leads to Corollary 1.2.
becomes large. This observation leads to Corollary 1.2.  can remain bounded in
can remain bounded in  only if the Riemann hypothesis is true, or if
only if the Riemann hypothesis is true, or if remains fortuitously bounded as an infinite sum over
remains fortuitously bounded as an infinite sum over  with no maximum in
with no maximum in .
.
Conversely,Riemann hypothesis implies
 (55)
(55)
According to (9) and our numerical calculation shown in Figure 3,the zeros  explored to large k by
explored to large k by

Figure 3.Shown are the absolute values of the Fourier coefficients  of
of  obtained by a Fast Fourier Transform (FFT) of (52) on the computational domain (53), where
obtained by a Fast Fourier Transform (FFT) of (52) on the computational domain (53), where ,
, covers 32 periods of
covers 32 periods of  (dots), on the basis of the 37,607,912,2019 primes up to 1,000,000,000,0039. The resulting spectrum is compared with the exact spectra
(dots), on the basis of the 37,607,912,2019 primes up to 1,000,000,000,0039. The resulting spectrum is compared with the exact spectra  of the
of the  given by the analytic expression (54) for
given by the analytic expression (54) for 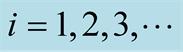 (continuous line). Shown are also the individual spectra of
(continuous line). Shown are also the individual spectra of  for
for  and 15 associated with the zeros
and 15 associated with the zeros ,
, and
and . The match between the computed and exact spectra accurately identifies the first 21 harmonics of
. The match between the computed and exact spectra accurately identifies the first 21 harmonics of  in
in  out of 22 shown, corresponding to the first 21 nontrivial zeros
out of 22 shown, corresponding to the first 21 nontrivial zeros  of
of .
.
existing numerical experiments effectively probe (and constrain) a distribution in primes which extends exponentially large in k.
Acknowledgements
The author gratefully acknowledges stimulating discussions with Fabian Ziltener and Anton F.P. van Putten. Some of the manuscript was prepared at the Korea Institute for Advanced Study, Dongdaemun-Gu, Seoul. This research was supported in part by the National Science Foundation through TeraGrid resources provided by Purdue University under grant number TG-DMS100033. We specifically acknowledge the assistance of VickiHalberstadt,RichRaymond and KimberlyDillman. The computations have been carried out using Lahey Fortran 95.
NOTES
1When  is an integer,
is an integer, is one-half the surface area of
is one-half the surface area of .
.