1. Introduction and Preliminaries
Different algebras began to be used in the thirties as a tool for the analysis and design of digital circuits. One of the pioneers in this field was C. E. Shannon, who in 1938 applied Boolean algebras in his work “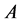 Symbolic Analysis of Change and Retransmission circuits”. Even though technology has changed substantially, these algebras still play a very important role in this field. In contrast, the use of ternary algebras has been much more limited, and the first applications of trivaluada logic to switching circuits were made by Goto in 1948. He worked with the algebra
Symbolic Analysis of Change and Retransmission circuits”. Even though technology has changed substantially, these algebras still play a very important role in this field. In contrast, the use of ternary algebras has been much more limited, and the first applications of trivaluada logic to switching circuits were made by Goto in 1948. He worked with the algebra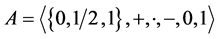 , of type
, of type , where
, where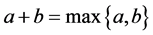 ,
, 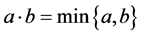 ,
,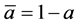 . He interpreted
. He interpreted 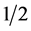 as an indefinite value, and used it to represent a transition state between 0 and 1. In addition, by means of the resolution of trivalued logic equations, he managed to derive the necessary conditions to prevent hazardous behavior in sequential relay contact networks. In 1959, Muller worked with this same ternary algebra, and applied it to the study of the transient phenomena in switching circuits, and observed, among other things, that it satisfies Kleene’s law:
as an indefinite value, and used it to represent a transition state between 0 and 1. In addition, by means of the resolution of trivalued logic equations, he managed to derive the necessary conditions to prevent hazardous behavior in sequential relay contact networks. In 1959, Muller worked with this same ternary algebra, and applied it to the study of the transient phenomena in switching circuits, and observed, among other things, that it satisfies Kleene’s law: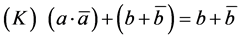 .
.
In 1964, Yoeli and Rinon applied them to the study of static hazards in combinational switching circuits. In 1965, Eichelberger used them in the analysis of hazard phenomena in combinational and sequential switching circuits.
In 1983, Mukaidono studied a special class of ternary functions, the regular ones, and indicated a set of axioms to define a ternary algebra, calling the resulting algebra Kleene algebra with a centre. However, it was not until 1995 that Brozozowski and Serger presented them as a De Morgan algebra with an additional constant, 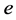 , which satisfies these identities:
, which satisfies these identities:
1) ,
,
2)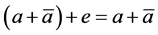 .
.
The same year Negulescu introduced the process spaces, a formalism which allows the modelling of the behaviour of interacting systems.
In 1996, Brozozowski, Lou and Negulescu considered certain subalgebras of the process spaces, i.e. the subset-pair algebras, and showed that each finite ternary algebra is isomorphic to a subset-pair algebra. In 1997, Esik showed that this property is valid for any ternary algebra and that, in general, each ternary algebra is isomorphic to an algebra of ternary functions, this result being analogous to Caley’s representation for Boolean algebras.
This class of algebras is applied in the detection of hazards in the combinational circuits, in the modelling of interacting systems by means of process spaces and in the analysis of asynchronous sequential circuits by means of Eichelberger’s method of ternary simulation, among other applications.
This article is organized as follows. Firstly, we summarize the main definitions and necessary results for a better comprehension of the article. In Section 2, we characterize the subdirectly irreducible algebras, examine the congruence lattice of a ternary algebra and establish properties of the variety . Finally, in Section 4, we indicate a construction of the free ternary algebra on a poset, and apply it to the free ternary algebra on one free generator and describe the poset of the join irreducible elements of the free ternary algebra on two free generators.
. Finally, in Section 4, we indicate a construction of the free ternary algebra on a poset, and apply it to the free ternary algebra on one free generator and describe the poset of the join irreducible elements of the free ternary algebra on two free generators.
Definition 1.1 A ternary algebra is an algebra 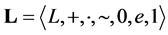 of type
of type 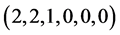 which satisfies these conditions:
which satisfies these conditions:
(T1) 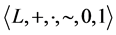 is a De Morgan algebra,
is a De Morgan algebra,
(T2) ![]() for all
for all![]() ,
,
(T3)![]() .
.
This class of algebras forms a variety which will be denoted by![]() .
.
The following properties are satisfied on![]() :
:
(T4) ![]() for all
for all![]() .
.
(T5) ![]() for all
for all![]() .
.
(T6) In each ternary algebra the only element that satisfies the condition ![]() is
is![]() .
.
(T7) Every finite ternary algebra has an odd number of elements.
(T8) There exist, up to isomorphism, one ternary algebra with five elements, two with seven, and four with nine.
(T9) For each odd natural number![]() , there exists at least one ternary algebra with
, there exists at least one ternary algebra with ![]() elements.
elements.
Clearly, (T4) is the dual property of (T2) while (T5) is equivalent to (T2).
Two well known examples of ternary algebras, of significant importance for the rest of this work, are:
Example 1.1
1) T0 is the ternary algebra![]() , where
, where![]() ,
, ![]() ,
, ![]()
![]() and
and![]() .
.
2) For each odd integer ![]() is the ternary algebra
is the ternary algebra![]() , where
, where![]() ,
,![]()
![]() .
.
2. The Congruence Lattice and Subdirectly Irreducible Algebras
In order to characterize the subdirectly irreducible ternary algebras we first observe that the ternary algebras arises from Kleene algebras endowed with a nullary operation.
Definition 2.1 A Kleene algebra ![]() is a De Morgan algebra which satisfies the property
is a De Morgan algebra which satisfies the property ![]()
![]() for every
for every![]() .
.
Definition 2.2 A Kleene algebra ![]() is centered if there exists an element
is centered if there exists an element ![]() such that
such that![]() ,
, ![]() is said the centre of
is said the centre of![]() .
.
We represent this class of algebras by![]() .
.
Remark 2.1 From Definitions 2.1 y 2.2 we have that:
1) If![]() , then the reduct
, then the reduct![]() , with centre in
, with centre in![]() .
.
2) If ![]() with centre in
with centre in![]() , entonces
, entonces![]() .
.
Well known results from Kleene algebra theory allow us to state the following:
Theorem 2.1 The only subdirectly irreducible centered Kleene algebra is the three-elements chain.
As a direct consequence of Theorem 2.1, we can establish
Corollary 2.1 The only subdirectly irreducible ternary algebra is![]() .
.
The preceding results and some from universal algebra allow us to ensure that:
Theorem 2.2
1) The simple algebras in this variety coincide with the subdirectly irreducible.
2) Variety ![]() is semisimple, residually finite and locally finite.
is semisimple, residually finite and locally finite.
Besides, with respect to the directly indecomposable algebras we can state that:
Theorem 2.3 In ![]() there exist directly indecomposable algebras which are not subdirectly irreducible.
there exist directly indecomposable algebras which are not subdirectly irreducible.
Proof. Any ternary algebra ![]() with
with ![]() a prime number greater than or equal to 3 is directly indecomposable but not subdirectly irreducible.
a prime number greater than or equal to 3 is directly indecomposable but not subdirectly irreducible. ![]()
From the above results we can conclude that:
Corollary 2.2 Variety ![]() is not directly representable.
is not directly representable.
Lattice ![]()
Now we will consider the congruence lattice of a ternary algebra![]() ,
, ![]() , and will establish some of its most relevant properties.
, and will establish some of its most relevant properties.
Theorem 2.4 Variety ![]() is not congruence-permutable.
is not congruence-permutable.
Proof. In the ternary algebra![]() , the congruences
, the congruences ![]() associated to partitions
associated to partitions
![]() and
and ![]() of the set
of the set ![]() respectively, satisfy that
respectively, satisfy that
![]() ,
,
Theorem 2.5 Variety ![]() is not congruence-uniform.
is not congruence-uniform.
Proof. It is sufficient to consider the equivalence classes ![]() and
and ![]() in the congruence
in the congruence ![]() considered in the proof of the theorem 2.4.
considered in the proof of the theorem 2.4. ![]()
Theorem 2.6 Variety ![]() is not congruence-regular.
is not congruence-regular.
Proof. In the ternary algebra![]() , it is sufficient to consider the congruences
, it is sufficient to consider the congruences ![]() associated to partitions
associated to partitions ![]() and
and ![]() of the set
of the set![]() , respectively.
, respectively. ![]()
As a direct consequence of Theorems 2.4 y 2.5, we can formulate:
Corollary 2.3 Variety ![]() is neither arithmetic nor discriminatory.
is neither arithmetic nor discriminatory.
The equations that define the principal congruences in the De Morgan algebras obtained by H. P. Sankappanavar in [2] allows the following:
Theorem 2.7 Variety ![]() has equationally definable principal congruences.
has equationally definable principal congruences.
From the results obtained by A. Day in 1971 [3] , and for W. J. Blok y D. Pigozzi in 1982 [4] , we can conclude that:
Theorem 2.8
1) Variety ![]() is congruence-distributive, it has the congruence extension property and the principal congruence extension property.
is congruence-distributive, it has the congruence extension property and the principal congruence extension property.
2) ![]() for all
for all![]() , being
, being ![]() a subalgebra of
a subalgebra of ![]() and
and![]() .
.
In addition, taking into account the characterization given by P. Kholer y D. Pigozzi in 1980 [5] , we have that:
Theorem 2.9 For all![]() ,
, ![]() is a
is a ![]() -semilattice with dual relative pseudo-complement, where
-semilattice with dual relative pseudo-complement, where ![]() is the set of the finitely generated congruences of the algebra
is the set of the finitely generated congruences of the algebra![]() .
.
3. Free Ternary Algebras over an Poset
In 1945, R. Dilworth [6] introduced the notion of free lattice over a poset. Later on, this subject was studied by many authors and in different classes of algebras. In this section we indicate a construction of the free ternary algebra over a poset, a result that generalizes those obtained by R. Balbes over free ternary algebras [7] .
Let ![]() be a variety of similar algebras which have an underlying ordered structure definable by a set of equations
be a variety of similar algebras which have an underlying ordered structure definable by a set of equations![]() ,
, ![]() , which are in terms of the algebra operations. The notion of free algebra over an poset
, which are in terms of the algebra operations. The notion of free algebra over an poset ![]() on
on ![]() can be defined as follows:
can be defined as follows:
Definition 3.1 A![]() —algebra
—algebra ![]() is free over
is free over ![]() if it satisfies the conditions that follow:
if it satisfies the conditions that follow:
(L1) there exists an order-embedding ![]() such that
such that ![]() where
where ![]() is the
is the![]() —subalgebra of
—subalgebra of ![]() generated by
generated by![]() ,
,
(L2) for each![]() —algebra
—algebra ![]() and each increasing function
and each increasing function![]() , there exists a homomorphism
, there exists a homomorphism ![]() such that
such that![]() .
.
Remark 3.1 It is clear that:
1) If the free algebra over an poset ![]() exists, it is unique up to isomorphism.
exists, it is unique up to isomorphism.
2) The homomorphism ![]() is unique.
is unique.
3) If ![]() is an poset of cardinality
is an poset of cardinality![]() ,
, ![]() , and the order over
, and the order over ![]() is the identity, then
is the identity, then ![]() is the free algebra with a set of
is the free algebra with a set of ![]() free generators.
free generators.
4) In variety ![]() each algebra has a underlying ordered structure defined by the equation
each algebra has a underlying ordered structure defined by the equation ![]() if, and only if,
if, and only if,![]() .
.
In what follows, we determine the structure of![]() .
.
3.1. Construction of the Free Ternary Algebra over a Poset I
A. Figallo Jr. and A. Ziliani in [8] construct the free algebra over a poset in finitely generated varieties; by using a similar argument, we indicate a construction of the free ternary algebra over a poset.
We consider a poset![]() , the set
, the set ![]() of the increasing functions of
of the increasing functions of ![]() in the ternary algebra
in the ternary algebra ![]() and the function
and the function ![]() defined by
defined by ![]() where
where ![]() is such that
is such that ![]() for each
for each ![]() and for each
and for each![]() .
.
Theorem 3.1 The free ternary algebra ![]() over the poset
over the poset ![]() is
is ![]() where
where![]() .
.
Proof.
(L1) It is clear that if ![]() are such that
are such that![]() , then
, then![]() .
.
Conversely, let us suppose that![]() , the function
, the function ![]() defined by
defined by
![]()
is an increasing function such that![]() . From what has been stated, we conclude that
. From what has been stated, we conclude that ![]() on
on ![]() if, and only if,
if, and only if, ![]() on
on![]() , from which it turns out that
, from which it turns out that ![]() is an order isomorphism, such that
is an order isomorphism, such that
![]() . Therefore, (L1) holds.
. Therefore, (L1) holds.
(L2) Let ![]() be a ternary algebra and
be a ternary algebra and ![]() an increasing function, by Corollary 2.1,
an increasing function, by Corollary 2.1, ![]() is isomorphic to a subalgebra of
is isomorphic to a subalgebra of ![]() being X an arbitrary set, then there exists a subalgebra
being X an arbitrary set, then there exists a subalgebra ![]() of
of ![]() and an isomorphism
and an isomorphism![]() . We claim that there is a homomorphism
. We claim that there is a homomorphism ![]() such that
such that![]() . Indeed, for each
. Indeed, for each
![]() let us consider the function
let us consider the function ![]() defined by
defined by![]() . It is easily shown that
. It is easily shown that
![]() for each
for each![]() , therefore
, therefore ![]() defined by
defined by ![]() is function. From what has been stated it follows that the function
is function. From what has been stated it follows that the function ![]() defined by
defined by ![]() is a homomorphism such that
is a homomorphism such that![]() .
.
In addition, as ![]() is a homomorphism and
is a homomorphism and ![]() is a ternary subalgebra of
is a ternary subalgebra of ![]() which
which
contains![]() , it turns out that
, it turns out that![]() . Therefore, (L2) holds.
. Therefore, (L2) holds. ![]()
3.2. Free Ternary Algebra on One Free Generator
If ![]() is a ternary algebra and
is a ternary algebra and![]() , we denote by
, we denote by ![]() the ternary algebra generated by the set
the ternary algebra generated by the set ![]() and by
and by ![]() the free ternary algebra with
the free ternary algebra with ![]() as the set of free generators, and we set
as the set of free generators, and we set ![]() and
and![]() .
.
In [7] , R. Balbes proves that![]() , we apply this result and those ob-
, we apply this result and those ob-
tained before in order to get the free ternary algebra on one free generator.
Let ![]() and
and ![]() where
where ![]() are defined as follows
are defined as follows![]() ,
, ![]() y
y ![]()
Let ![]() defined by
defined by ![]() where
where ![]() such that
such that![]() ,
, ![]() y
y![]() . Some of the elements of
. Some of the elements of ![]() are specified in the Table 1.
are specified in the Table 1.
Then, the free ternary algebra on one free generator is:
![]()
where![]() . Then,
. Then, ![]() which coincides with the result obtained by R. Balbes en [7] .
which coincides with the result obtained by R. Balbes en [7] .
The algebra ![]() is that indicated in Figure 1.
is that indicated in Figure 1.
3.3. The Poset of the Join Irreducible Elements of the Free Ternary Algebra on Two Free Generators
In [7] R. Balbes proves that the poset of the join irreducible elements of the free ternary algebra ![]() with a finite set of free generators X is isomorphic with
with a finite set of free generators X is isomorphic with![]() , being
, being
![]() and,
and,
ordered by the relation ![]() if, and only if,
if, and only if,![]() .
.
We apply this result and those obtained above in order to determine the poset of the join irreducible elements of a free ternary algebra on two free generators. We consider the set ![]() ordered by the identity relation,
ordered by the identity relation, ![]() where each of the functions are defined in the Table 2, and
where each of the functions are defined in the Table 2, and ![]() defined by
defined by
![]()
Figure 1. The free ternary algebra on one free generator.
![]()
where ![]() such that
such that ![]() for each
for each![]() .
.
In the Table 3, we specify some of the elements of![]() .
.
![]()
Figure 2. The poset of join irreducible elements of the free ternary algebra on two free generators.
Then,
![]()
The poset ![]() coincides with that obtained by R. Balbes in [7] and it is the one indicated in Figure 2.
coincides with that obtained by R. Balbes in [7] and it is the one indicated in Figure 2.