Mean Square Convergent Finite Difference Scheme for Stochastic Parabolic PDEs ()
1. Introduction
Stochastic partial differential equations (SPDEs) frequently arise from applications in areas such as physics, engineering and finance. However, in many cases it is difficult to derive an explicit form of their solution. In recent years, some of the main numerical methods for solving stochastic partial differential equations (SPDEs), like finite difference and finite element schemes, have been considered [1] -[9] , e.g. [10] -[12] , based on a finite difference scheme in both space and time. It is well known that explicit time discretization via standard methods (e.g., as the Euler-Maruyama method) leads to a time step restriction due to the stiffness originating from the discretization of the diffusion operator (e.g. the Courant-Friedrichs-Lewy (CFL)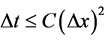 , where Δt and Δx are the time and space discretization, respectively). Mohammed [8] discussed stochastic finite difference
, where Δt and Δx are the time and space discretization, respectively). Mohammed [8] discussed stochastic finite difference
schemes by three points under the following condition of stability: 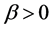
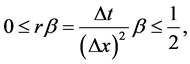 and five points under this condition of stability:
and five points under this condition of stability: 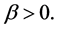
 Our aim of this paper is to use the sto-
Our aim of this paper is to use the sto-
chastic finite difference schemes by seven points that are strong convergences to our problem and much better stability properties than three and five points.
This paper is organized as follows. In Section 2, some important preliminaries are discussed. In Section 3, the Finite Difference Scheme with seven points for solving stochastic parabolic partial differential equation is discussed. In Section 4, some case studies are discussed. The general conclusions are presented in the last section.
2. Preliminaries
In this section we will state some definition from [9] as follow:
Definition 1. A sequence of r.v’s  converges in mean square
converges in mean square  to a random variable X if:
to a random variable X if:
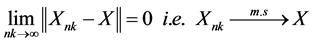
Definition 2. A stochastic difference scheme  approximating SPDE
approximating SPDE 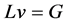 is consistent in mean square at time
is consistent in mean square at time , if for any differentiable function
, if for any differentiable function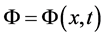 , we have in mean square:
, we have in mean square:
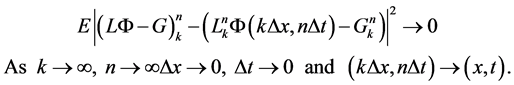
Definition 3. A stochastic difference scheme is stable in mean square if there exist some positive constants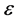 ,
,  and constants k, b such that:
and constants k, b such that:

Definition 4. A stochastic difference scheme ![]() approximating SPDE
approximating SPDE ![]() is convergent in mean square at time
is convergent in mean square at time![]() , if:
, if:
![]()
3. Stochastic Parabolic Partial Differential Equation (SPPDE)
In this section the stochastic finite difference method is used for solving the SPPDE. Consider the following stochastic parabolic partial differential equation in the form:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
where ![]() is a white noise stochastic process and
is a white noise stochastic process and ![]() are constants.
are constants.
3.1. Stochastic Difference Scheme (with Seven Points)
For the Equations (1)-(3) the difference scheme is:
![]() (4)
(4)
![]() (5)
(5)
![]() , (6)
, (6)
where ![]() and it can be written in the form:
and it can be written in the form:
![]() (7)
(7)
3.1.1. Consistency
In this subsection we study the consistency in mean square sense of the Equation (7).
Theorem 3.1. The stochastic difference scheme (7) is consistent in mean square sense.
Proof. Assume that ![]() be a smooth function then:
be a smooth function then:
![]()
![]()
then we have:
![]()
since:
![]() ,
,
then:
![]()
and from the inequality
![]()
Applying in the part
![]()
and ![]() is deterministic function we have:
is deterministic function we have:
![]()
as time![]() ,
, ![]() ,
, ![]() , and
, and![]() , then:
, then:
![]()
hence the stochastic difference scheme (7) is consistent in mean square sense.
3.1.2
. Stability
Theorem 3.2. The stochastic difference scheme (7) is stable in mean square sense.
Proof. Since
![]()
then:
![]()
Since ![]() is normally distributed with mean zero and variance
is normally distributed with mean zero and variance ![]() increments of the winner process are independent
increments of the winner process are independent ![]() and
and
![]() .
.
Then we have:
![]()
![]()
since:
![]()
then:
![]()
then:
![]()
![]()
Now with:
![]()
then:
![]()
Hence:
![]()
It is enough to select ![]() such that:
such that: ![]() for all k then we put
for all k then we put ![]() to get:
to get:
![]() (8)
(8)
Hence the scheme is conditionally stable with ![]() and
and ![]() in mean square sense with the condition:
in mean square sense with the condition:
![]()
3.1.3
. Convergence
Theorem 3.3. The random difference scheme (7) is convergent in mean square sense
Proof.
![]()
Since the scheme is consistent then we have ![]() then we obtain
then we obtain
![]()
as![]() ,
, ![]() and
and ![]() and since the scheme is stable then
and since the scheme is stable then ![]() is bounded hence:
is bounded hence:
![]()
then the random difference scheme (7) is convergent in mean square sense.
4. Applications
Consider the linear heat equation with multiplicative noise in this form
![]()
The SFDS with seven points is:
![]()
Since the stability condition from Theorem 3.2 is:
![]()
let ![]() then
then ![]() therefore:
therefore:
![]()
then we have:
![]()
In Theorem 3.8, we assumed that:
![]()
Therefore, for different amount N, we can derive low boundary of ![]() (see Table 1).
(see Table 1).
On the other hand, in Equation (8), we had
![]()
and for stability, we represent y for different N (see Figure 1).
5. Conclusion and Future Works
The stochastic parabolic partial differential equations can be solved numerically using the stochastic difference (with seven points) method in mean square sense. More complicated problems in linear stochastic parabolic partial differential equations can be studied using finite difference method in mean square sense. The techniques of solving nonlinear stochastic partial differential equations using the finite difference method with the aid of mean square calculus can enhance greatly the treatment of stochastic partial differential equations in mean square sense.