Currency Derivatives Pricing for Markov-Modulated Merton Jump-Diffusion Spot Forex Rate ()
1. Introduction
The existing academic literature on the pricing of foreign currency options could be divided into two categories: 1) both domestic and foreign interest rates were assumed to be constant whereas the spot exchange rate was assumed to be stochastic (see, e.g., Jarrow et al. (1981, [1] ); 2) models for pricing foreign currency options incorporate stochastic interest rates, and are based on Merton’s (1973, [2] ) stochastic interest rate model for pricing equity options (see, e.g., Grabbe 1983, [3] ; Adams et al. (1987, [4] ). In both cases, this pricing approach did not integrate a full-term structure model into the valuation framework. To our knowledge, Amin et al. (1991, [5] ) were the first to start discussing and building a general framework to price contingent claims on foreign currencies under stochastic interest rates using the Heath et al. (1987) model of term structure. Melino et al. (1991, [6] ) examined the foreign exchange rate process, (under a deterministic interest rate), underlying observed option prices and Rumsey (1991, [7] ) considered cross-currency options. Mikkelsen (2001, [8] ) investigated simulation cross-currency options using market models of interest rates and deterministic volatilities for spot exchange rates. Schlogl (2002, [9] ) extended market models to a cross-currency framework. Piterbarg (2005, [10] ) developed a model for cross-currency derivatives such as PRDC swaps with calibration for currency options; he used neither market models nor stochastic volatility models. In Garman et al. (1983, [11] ) and Grabbe (1983, [3] ), foreign exchange option valuation formulas were derived under the assumption that the exchange rate followed a diffusion process with continuous sample paths. Takahashi et al. (2006, [12] ) proposed a new approximation formula for the valuation of currency options using jump-diffusion stochastic volatility processes for spot exchange rates in a stochastic interest rates environment. In particular, they applied the market models developed by Brace et al. (1998), Jamshidian (1997, [13] ) and Miltersen et al. (1997, [14] ) to model the term structure of interest rates. Also, Ahn et al. (2007, [15] ) derived explicit formulas for European foreign exchange call and put options values when the exchange rate dynamics is governed by jump-diffusion processes. Hamilton (1988) was the first to investigate the term structure of interest rates by rational-expectations econometric analysis of changes in regime. Goutte et al. (2011, [16] ) studied foreign exchange rates using a modified Cox-Ingersoll- Ross model under a Hamilton Markov regime switching framework. Zhou et al. (2012, [17] ) considered an accessible implementation of interest rate models with regime-switching. Siu et al (2008, [18] ) considered pricing currency options under a two-factor Markov-modulated stochastic volatility model. Swishchuk and Elliott applied hidden Markov models for pricing options in [19] . Bo et al. (2010, [20] ) discussed a Markov-modulated jump-diffusion, (modeled by a compound Poisson Process), for currency option pricing. We noted that currency derivatives for domestic and foreign equity markets and for the exchange rate between the domestic currency and a fixed foreign currency with constant interest rates were discussed in Bjork (1998, [21] ). We also mentioned that currency conversion for forward and swap prices with constant domestic and foreign interest rates were discussed in Benth et al. (2008, [22] ).
In this article we generalize results in [20] in case when dynamics of FX rate is driven by a general Merton jump-diffusion process ([23] ). Main results of our research are as follows:
1) In section 2, we generalize formulas in [20] for Esscher transform parameters assuring that martingale condition for discounted foreign exchange rate is a martingale for a general Merton jump-diffusion process (see (30)). Using these values of parameters (see (38), (39)), we proceed to a risk-neural measure and provide new formulas for the distribution of jumps ((36)), the mean jump size (see (20)), and the Poisson Process intensity with respect to this measure (see (19)). At the end of section 2, pricing formulas for a European call foreign exchange option are given (They are similar to those in [20] , but the mean jump size and the Poisson Process intensity with respect to the new risk-neutral measure are different).
2) In section 3, we apply Formulas (18)-(20), (38)-(39) to a particular case of the exponential distribution (see (50)) of jumps (see (53)-(55)).
3) In section 4, we provide numerical simulations of European call foreign exchange option prices for different parameters: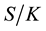 , where
, where 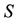 is the initial spot FX rate, and
is the initial spot FX rate, and 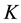 is the strike FX rate for a maturity time
is the strike FX rate for a maturity time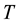 .
.
2. Currency Option Pricing for Merton Jump-Diffusion Processes
Let 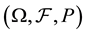 be a complete probability space with a probability measure
be a complete probability space with a probability measure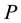 . Consider a continuous-time,
. Consider a continuous-time,
finite-state Markov chain 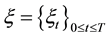 on
on 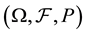 with a state space
with a state space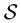 , the set of unit vectors
, the set of unit vectors
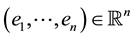 with a rate matrix
with a rate matrix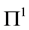 . The dynamics of the chain are given by:
. The dynamics of the chain are given by:
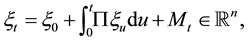 (1)
(1)
where 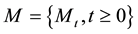 is a
is a 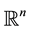 -valued martingale with respect to
-valued martingale with respect to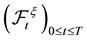 , the
, the 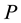 -augmentation of the
-augmentation of the
natural filtration![]() , generated by the Markov chain
, generated by the Markov chain![]() . Consider a Markov-modulated Merton jump- diffusion which models the dynamics of the spot FX rate, given by the following stochastic differential equation (in the sequel SDE, see [20] ):
. Consider a Markov-modulated Merton jump- diffusion which models the dynamics of the spot FX rate, given by the following stochastic differential equation (in the sequel SDE, see [20] ):
![]() (2)
(2)
Here ![]() is drift parameter;
is drift parameter; ![]() is a Brownian motion,
is a Brownian motion, ![]() is the volatility;
is the volatility; ![]() is a Poisson Process with intensity
is a Poisson Process with intensity![]() ,
, ![]() is the amplitude of the jumps, given the jump arrival time. The distribution of
is the amplitude of the jumps, given the jump arrival time. The distribution of ![]() has a density
has a density![]() . The parameters
. The parameters![]() ,
, ![]() ,
, ![]() are modeled using the finite state Markov chain:
are modeled using the finite state Markov chain:
![]() (3)
(3)
The solution of (2) is![]() , (where
, (where ![]() is the spot FX rate at time
is the spot FX rate at time![]() ). Here
). Here ![]() is given by the formula:
is given by the formula:
![]() (4)
(4)
Note, that for the most of well-known distributions (normal, exponential distribution of![]() , etc)
, etc) ![]() is not a Lévy process (see definition of Lévy process in [24] , the condition L3), since
is not a Lévy process (see definition of Lévy process in [24] , the condition L3), since ![]() for small
for small![]() , but
, but
probability of jumps with even 0 amplitude is a positive constant, depending on a type of distribution. We call the process (4) as Merton jump-diffusion process (see [23] , section 2, Formulas 2, 3)
There is more than one equivalent martingale measure for this market driven by a Markov-modulated jump- diffusion model. We shall define the regime-switching generalized Esscher transform to determine a specific equivalent martingale measure.
Using Ito’s formula we can derive a stochastic differential equation for the discounted spot FX rate. To define the discounted spot FX rate we need to introduce domestic and foreign riskless interest rates for bonds in the domestic and foreign currency.
The domestic and foreign interest rates![]() ,
, ![]() are defined using the Markov chain
are defined using the Markov chain ![]() (see [20] ):
(see [20] ):
![]()
![]()
The discounted spot FX rate is:
![]() (5)
(5)
Using (5), the differentiation formula, see Elliott et al. (1982, [25] ) and the stochastic differential equation for the spot FX rate (2) we find the stochastic differential equation (SDE) for the discounted spot FX rate:
![]() (6)
(6)
To derive the main results consider the log spot FX rate,
![]()
Using the differentiation formula:
![]()
where ![]() are the continuous and diffusion part of
are the continuous and diffusion part of![]() . They are given in (7), (8):
. They are given in (7), (8):
![]() (7)
(7)
![]() (8)
(8)
Let ![]() denote the
denote the ![]() -augmentation of the natural filtration
-augmentation of the natural filtration![]() , generated by
, generated by![]() . For each
. For each
![]() set
set![]() . Let us also define two families of regime switching parameters
. Let us also define two families of regime switching parameters![]() ,
,
![]() :
:![]() ,
,![]() ,
,![]() .
.
Define a random Esscher transform ![]() on
on ![]() using these families of parameters
using these families of parameters![]() ,
, ![]() (see [20] [26] [27] for details):
(see [20] [26] [27] for details):
![]() (9)
(9)
The explicit formula for the density ![]() of the Esscher transform is given in the following Theorem. A similar statement is proven for the log-normal distribution in [20] . The formula below can be obtained by another approach, considered by Elliott and Osakwe ([28] ).
of the Esscher transform is given in the following Theorem. A similar statement is proven for the log-normal distribution in [20] . The formula below can be obtained by another approach, considered by Elliott and Osakwe ([28] ).
Theorem 2.1. For ![]() density
density ![]() of Esscher transform defined in (9) is given by:
of Esscher transform defined in (9) is given by:
![]() (10)
(10)
In addition, the random Esscher transform density ![]() (see (9), (10)) is an exponential
(see (9), (10)) is an exponential ![]() mar- tingale and admits the following SDE
mar- tingale and admits the following SDE
![]() (11)
(11)
Proof Theorem 2.1. The compound Poisson Process, driving jumps![]() , and the Brownian motion
, and the Brownian motion ![]() are independent processes. As a result:
are independent processes. As a result:
![]() (12)
(12)
Let us calculate:
![]()
Write
![]()
Using the differentiation rule (see [25] ) we obtain the following representation of![]() :
:
![]() (13)
(13)
where
![]()
is a martingale with respect to![]() . Using this fact and (13) we obtain:
. Using this fact and (13) we obtain:
![]() (14)
(14)
We have from the differentiation rule:
![]() (15)
(15)
where ![]() is the volatility of a market. Substituting (14) and (15) into (12) we obtain:
is the volatility of a market. Substituting (14) and (15) into (12) we obtain:
![]() (16)
(16)
Substituting (16) to the expression for ![]() in (9) we have:
in (9) we have:
![]() (17)
(17)
If we present ![]() in the form
in the form ![]() (see (17)) and and apply differentiation rule we obtain SDE (11). It follows from (11) that
(see (17)) and and apply differentiation rule we obtain SDE (11). It follows from (11) that ![]() is a martingale.
is a martingale.
We shall derive the following condition for the discounted spot FX rate ((5)) to be martingale. These conditions will be used to calculate the risk-neutral Esscher transform parameters![]() ,
, ![]() and give to the measure
and give to the measure![]() . Then we shall use these values to find the no-arbitrage price of European call currency derivatives.
. Then we shall use these values to find the no-arbitrage price of European call currency derivatives.
Theorem 2.2. Let the random Esscher transform be defined by (9). Then the martingale condition (for![]() , see (5)) holds if and only if Markov modulated parameters
, see (5)) holds if and only if Markov modulated parameters ![]() satisfy for all
satisfy for all ![]() the condition:
the condition:
![]() (18)
(18)
where the random Esscher transform intensity ![]() of the Poisson Process and the main percentage jump size
of the Poisson Process and the main percentage jump size ![]() are respectively given by
are respectively given by
![]() (19)
(19)
![]() (20)
(20)
as long as![]() .
.
Proof of Theorem 2.2. The martingale condition for the discounted spot FX rate![]() :
:
![]() (21)
(21)
To derive such a condition Bayes formula is used:
![]() (22)
(22)
taking into account that ![]() is a martingale with respect to
is a martingale with respect to![]() , so:
, so:
![]() (23)
(23)
Using Formula (5) for the solution of the SDE for the spot FX rate, we obtain an expression for the discounted spot FX rate in the following form:
![]() (24)
(24)
Then, using (10), (24) we can rewrite (23) in the following form:
![]()
Using expression for characteristic function of Brownian motion (see (15)) we obtain:
![]() (27)
(27)
Using (14) we have:
![]() (28)
(28)
Substituting (27), (28) into (26) we obtain finally:
![]() (29)
(29)
From (29) we get the martingale condition for the discounted spot FX rate:
![]() (30)
(30)
Prove now, that under the Esscher transform the new Poisson Process intensity and the mean jump size are given by (19), (20).
Note that ![]() is the jump part of Lévy process in the formula (4) for the solution of SDE for spot FX rate. We have:
is the jump part of Lévy process in the formula (4) for the solution of SDE for spot FX rate. We have:
![]() (31)
(31)
where ![]() is the initial probability measure,
is the initial probability measure, ![]() is a new risk-neutral measure. Substituting the density of the Esscher transform (10) into (31) we have:
is a new risk-neutral measure. Substituting the density of the Esscher transform (10) into (31) we have:
![]() (32)
(32)
Using (14) we obtain:
![]() (33)
(33)
Putting (33) to (32) and taking into account characteristic function of Brownian motion (see (15)) we have:
![]() (34)
(34)
Return to the initial measure![]() , but with different
, but with different![]() . We obtain:
. We obtain:
![]() (35)
(35)
Formula (19) for the new intensity ![]() of the Poisson Process follows directly from (34), (35). The new density of jumps
of the Poisson Process follows directly from (34), (35). The new density of jumps ![]() is defined from (34), (35) by the following formula:
is defined from (34), (35) by the following formula:
![]() (36)
(36)
Calculate now the new mean jump size given jump arrival with respect to the new measure![]() :
:
![]() (37)
(37)
So, we can rewrite martingale condition for the discounted spot FX rate in the form in (18), where ![]() are given by (19), (20) respectively.
are given by (19), (20) respectively.
Using (30) we have the following formulas for the families of the regime switching parameters satisfying the martingale condition (18):
![]() (38)
(38)
![]() (39)
(39)
where ![]() is any constant. Note again, that the choice for these parameters is not unique.
is any constant. Note again, that the choice for these parameters is not unique.
In the next section we shall apply these Formulas (38), (39) to the exponential distribution of jumps.
We now proceed to the general formulas for European calls (see [20] [23] ). For the European call currency options with a strike price ![]() and the time of expiration
and the time of expiration ![]() the price at time zero is given by:
the price at time zero is given by:
![]() (40)
(40)
Let ![]() denote the occupation time of
denote the occupation time of ![]() in state
in state ![]() over the period
over the period![]() . We introduce several new quantities that will be used in future calculations:
. We introduce several new quantities that will be used in future calculations:
![]() (41)
(41)
where![]() ;
;
![]() (42)
(42)
![]() (43)
(43)
![]() (44)
(44)
![]() (45)
(45)
where ![]() is the variance of the distribution of the jumps.
is the variance of the distribution of the jumps.
![]() (46)
(46)
where ![]() is the number of jumps in the interval
is the number of jumps in the interval![]() ,
, ![]() is the number of states of the Markov chain
is the number of states of the Markov chain![]() .
.
From the pricing formula in Merton (1976, [23] ) let us define (see [20] )
![]() (47)
(47)
where ![]() is the standard Black-Scholes price formula (see [21] ) with initial spot FX rate
is the standard Black-Scholes price formula (see [21] ) with initial spot FX rate![]() , strike price
, strike price![]() , risk-free rate
, risk-free rate![]() , volatility square
, volatility square ![]() and time
and time ![]() to maturity.
to maturity.
Then, the European style call option pricing formula takes the form (see [20] ):
![]() (48)
(48)
where ![]() is the joint probability distribution density for the occupation time, which is determined by the following characteristic function (see [28] ):
is the joint probability distribution density for the occupation time, which is determined by the following characteristic function (see [28] ):
![]() (49)
(49)
where ![]() is a vector of ones,
is a vector of ones, ![]() is a vector of transform variables,
is a vector of transform variables,
![]() .
.
3. Currency Option Pricing for Exponential Processes
Because of the restriction ![]() we can not consider a double-exponential distribution of jumps (see [29] [30] ) in
we can not consider a double-exponential distribution of jumps (see [29] [30] ) in![]() . Let us consider exponential distribution instead. It is defined by the following formula of density function:
. Let us consider exponential distribution instead. It is defined by the following formula of density function:
![]() (50)
(50)
The mean value of this distribution is:
![]() (51)
(51)
The variance of this distribution is:
![]() (52)
(52)
The exponential distribution like the double-exponential distribution has also memorylessness property.
Let us derive the martingale condition and formulas for the regime-switching Esscher transform parameters in case of jumps driven by the exponential distribution. Using the martingale condition for discounted spot FX rate (30) we obtain:
![]() (53)
(53)
where we have such a restriction(and in the sequel):![]() .
.
Using (19), (20) the random Esscher transform intensity ![]() of the Poisson Process and the main percentage jump size
of the Poisson Process and the main percentage jump size ![]() are respectively given by:
are respectively given by:
![]() (54)
(54)
![]() (55)
(55)
Using (39) we have the following formula for the families of regime switching Esscher transform parameters satisfying martingale condition (53):
![]() (56)
(56)
Let us simplify (56):
![]() (57)
(57)
The formula for ![]() in this case is the same as in (38).
in this case is the same as in (38).
With respect to to such values of the regime switching Esscher transform parameters we have from (54), (55), (57):
![]() (58)
(58)
when we proceed to a new risk-neutral measure ![]() we have the new
we have the new ![]() in (50). Using (36) we obtain:
in (50). Using (36) we obtain:
![]() (59)
(59)
From (59) we arrive at interesting conclusion: ![]() depends on time
depends on time![]() . So, now the distribution of jumps changes depending on time (it is not the case before for the log double-exponential distribution, where
. So, now the distribution of jumps changes depending on time (it is not the case before for the log double-exponential distribution, where ![]() was actually a constant, see [20] ). So, the compound Poisson Process depends not only on a number of jumps, but on moments of time when they arrive in this case. The same statement is true for the mean jump size in (55). But the pricing Formulas (40)-(48) are applicable to this case as well.
was actually a constant, see [20] ). So, the compound Poisson Process depends not only on a number of jumps, but on moments of time when they arrive in this case. The same statement is true for the mean jump size in (55). But the pricing Formulas (40)-(48) are applicable to this case as well.
In the numerical simulations, we assume that the hidden Markov chain has three states: up, down, side-way, and the corresponding rate matrix is calculated using real Forex data for the thirteen-year period: from January 3, 2000 to November 2013.
4. Numerical Simulations
In the Figures 1-3, we shall provide numerical simulations for the case when amplitude of jumps is described by
the exponential distribution. These plots show the dependence of a European call option price on![]() , where
, where ![]() is the initial spot FX rate (
is the initial spot FX rate (![]() in our simulations),
in our simulations), ![]() is a strike FX rate for various maturity times
is a strike FX rate for various maturity times![]() : 0.5, 1, 1.5 in years and various values of a parameter
: 0.5, 1, 1.5 in years and various values of a parameter![]() : 2.5, 3.5, 5 in the exponential distribution. Blue line stands for the exponential distribution of jumps, red-line is for the dynamics without jumps. From these plots, we can make a conclusion that it is important to incorporate a jump risk into the spot FX rate models (described by the Black-Scholes equation, without jumps red line on a plot is below the blue line standing for the exponential distributions of jumps).
: 2.5, 3.5, 5 in the exponential distribution. Blue line stands for the exponential distribution of jumps, red-line is for the dynamics without jumps. From these plots, we can make a conclusion that it is important to incorporate a jump risk into the spot FX rate models (described by the Black-Scholes equation, without jumps red line on a plot is below the blue line standing for the exponential distributions of jumps).