Solvability of the Economic Input-Output Equation by Time Irreversibility ()
1. Introduction
The purpose of this paper is to clarify a solvability condition of the economic input-output equation which was invented by
Wassily
Leontief
. This is achieved through adapting some interpretations of the equation.
In general, economic input-output analysis is affected by equilibrium economics, which is the mainstream of contemporary economics. For example,
Leontief
regarded input-output analysis as an example of general economic equilibrium theory.1 Thus, this analysis usually treats the economic input-output relation as the relationship between demand and supply, which is considered to be determined by the decision making of an economic agent.
However, this paper treats the economic input-output relation as a realized relationship between the source and result. This relationship is not based on the decision making of an agent. It is only a realized influential relation among commodities excluding decision making.
Moreover, usual input-output analysis often expresses the quantity of commodity by a monetary unit, but this supposition is not based on empiricism. Commodity is an entity only measured by its own unit. We will discuss input-output analysis under this supposition.
Based on these policies, we will start to reconstruct the description of the economic input-output structure.
We define output as the production of a commodity. Further, we define input as the use of a commodity which contributes to the production of the commodity.
The being which executes input or output is called an economic sector. We decide that one sector possesses only one kind of commodity,2 but we do not eliminate the possibility of different sectors possessing the same kind of commodity. A set of sectors targeted for description is called the relevant society. We assume there are n sectors in the relevant society and denote the relevant society by .
.
Moreover, we decide that a target term for description is called the relevant term. We assume that the relevant term is finite. This assumption is rewritten so that the relevant term always has a beginning and an end. This assumption does not threaten the validity of the description of an economic society because most scientists say that even the life of the earth is limited.
The sphere that satisfies both the relevant society and the relevant term is called the relevant space-time.
Next, we define concepts which appear in our input-output analysis.
Let Zij be the input quantity possessed by Sector i and contributing to the production of Sector j in the relevant space-time. In this paper, this is called the separate input quantity from Sector i to Sector j.
Let Xi be the sum of the separate input quantity possessed by Sector i in the relevant space-time, which is called the gross input quantity by Sector i in this paper. By the definition of gross input, we can see that
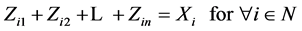 (1)
(1)
Let Yj be the output quantity produced by Sector j in the relevant space-time.
The relationships between separate inputs, gross inputs, and outputs can be summarized as in the following table.
We call this the input-output table.
Quantitatively, the existence of a commodity is expressed as a positive, and the absence of commodity is expressed as zero. Negative existence of commodity does not have an economic meaning. Hence, the quantity of input and output is non-negative. That is,
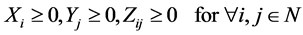 (2)
(2)
always holds.
However, we suppose that all sectors execute positive output in the relevant space-time. The reason for this supposition is to avoid complications of the following description. Using symbols, the supposition is denoted as
 (3)
(3)
Then, we consider the sources of possession of commodity in the relevant space-time. Output is one source, but not the only source. Commodities which exist before the relevant term or which are produced outside of the relevant society can also be sources. We decide that the sources excluding output in the relevant space-time are collectively called carried.
On the other hand, we consider the results of possession of commodity in the relevant space-time. Input is one result, but not the only result. Commodities which are used by a consumer, inputted after the relevant term, inputted outside of the relevant society, or never used can also be results. We decide that the results excluding input in the relevant space-time are collectively called surplus.3
Let Ψk be the carried quantity of Sector k, and Ωk be the surplus quantity of Sector k. As mentioned above, quantitatively, the existence of a commodity is expressed as a positive, and the absence of a commodity is expressed as zero. Negative existence of a commodity does not have an economic meaning. Thus,
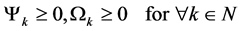 (4)
(4)
always holds.
Then, we define the disposal as a process from the source to the result.
If we trace the source of commodity inputted in the relevant space-time, it is only either outputted or carried. We call this the disposal comprehensibility principle.
We define a disposal from output to input as a circular disposal. We denote the circular disposal quantity of Agent k as ρk. Moreover, let αk be the quantity of commodity disposed from carried to input. Quantitatively, the disposal comprehensibility principle means

Note that if a commodity which is once inputted does not disappear, it is able to be inputted again or used outside of the relevant space-time. Nevertheless, this paper constructs a theory excluding the possibility of such duplicate uses. We call this supposition the disposal exclusivity principle. Quantitatively, the disposal exclusivity principle means
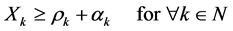
Considering both the disposal comprehensibility principle and the disposal exclusivity principle,

is satisfied.
If we trace the source of commodity that becomes surplus, it is only either outputted or carried. Let βk be the quantity of commodity disposed from output to surplus, and γk be the quantity of commodity disposed from carried to surplus. As in the case of input, considering both the disposal comprehensibility and exclusivity principle,

is satisfied.
On the other hand, if we trace the result of carried commodity in the relevant space-time, it is only either inputted or becomes surplus. αk refers to the quantity of commodity disposed from carried to input, and γk refers to the quantity of commodity disposed from carried to surplus. Therefore, considering both the disposal comprehensibility and exclusivity principle,

is satisfied.
If we trace the result of commodity outputted in the relevant space-time, it is only either inputted or becomes surplus. ρk refers to the quantity of commodity disposed from output to input, and βk refers to the quantity of commodity disposed from output to surplus. Therefore, considering both the disposal comprehensibility and exclusivity principle,
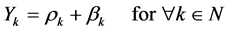
is satisfied.
We decide that ρk, αk, βk and γk are collectively called the disposal quantities. Based on their economic meanings,
 (5)
(5)
are always satisfied.
The relationships between the disposal quantities and other quantities are summarized in the following table.
We call this the disposal table of Sector k. Based on this table, it is obvious that
 (6)
(6)
is satisfied. That is, the gross quantity of sources of Sector k and the gross quantity of results of Sector k are equal. We call this proposition the law of gross disposal of Sector k.
2. Formalization of the Economic Input-Output Equation
Based on the preceding section, we will formalize the economic input-output equation.
First, we confirm that the gross quantity of sources of Sector k satisfies
 (7)
(7)
By Equations (3) and (4). Based on this, the self-sufficiency rate of Sector k is defined as
![]() 4 (8)
4 (8)
In short, the self-sufficiency rate refers to the percentage of output in the gross quantity of sources.
By Equations (3), (4) and (7), the self-sufficiency rate is limited to
![]() (9)
(9)
Considering Equations (1), (6) and (8), we can derive
![]() (10)
(10)
Next, based on Equation (3), the input coefficient from Sector i to Sector j is defined as
![]() (11)
(11)
In short, the input coefficient means separate input per one unit of output.
By Equations (2) and (3), the input coefficient is limited to
![]() (12)
(12)
Considering Equations (10) and (11), we can derive
![]()
We collect this formula from k = 1 to n and regard them as a system of simultaneous equations in![]() .5 It is the economic input-output equation.
.5 It is the economic input-output equation.
Let E be a unit matrix, and y be a column vector with the jth element equal to Yj, and ω be a column vector with the hth element equal to Ωh, and Λ be a square diagonal matrix with the hth diagonal element equal to λh, and ν be a square matrix with the (i,j)th element equal to νij. Then, the economic input-output equation can be denoted as
![]()
Moreover, Let pjh be the (j,h)th element of the inverse of E − Λν. The unique solution of the input-output equation can be expressed as
![]() (13)
(13)
pjh can be calculated from the self-sufficiency rate and the input coefficient of all sectors. Therefore, if the input-output equation has a unique solution, each output quantity can be calculated from the self-sufficiency rate, the input coefficient and surplus.
Note that Λν is a non-negative matrix because of Equations (9) and (12). Hence, E − Λν is a Z-matrix, which is defined as a square matrix in which the non-diagonal elements are all non-positive. Moreover, we can obtain Λω ≥ 0 from Equations (4) and (9). Considering this with Equation (3), we find that (E − Λν)y ≥ 0 where ∃y > 0 is satisfied. If this type of matrix is non-singular, pjh, which is an element of the inverse of E − Λν, has the following peculiarities.6
pjh is non-negative generally. Considering this with Equation (9), an increase of surplus does not decrease output unless it causes a variation of the self-sufficiency rate or the input coefficient.
In particular, pjj is 1 or more. Considering this with Equation (9), if one unit of surplus of a certain sector increases, their own output increases equal to the self-sufficiency rate or more unless it causes a variation of the self-sufficiency rate or the input coefficient.
Further, through Equations (11) and (13),
![]() (14)
(14)
is derived. Each separate input quantity can also be calculated from the self-sufficiency rate, the input coefficient and surplus.
Moreover, because of Equations (1) and (14),
![]() (15)
(15)
is derived. Each gross input quantity can also be calculated from the self-sufficiency rate, the input coefficient and surplus.
Furthermore, due to Equations (6), (13) and (15),
![]()
is derived. Each carried quantity can also be calculated from the self-sufficiency rate, the input coefficient and surplus.
Thus, if we can solve the economic input-output equation, we can calculate the total quantity of output, separate input, gross input, and carried from the quantity of surplus with the help of the self-sufficiency rate and the input coefficient.
3. Solvability Condition of the Economic Input-Output Equation
If the economic input-output equation has a unique solution, the amount of commodities each sector produces, uses for production and carries from the outside can be calculated. However, if it does not have a unique solution, we cannot execute such calculations, naturally. The effectiveness of the input-output equation depends on the solvability of the equation. Hence, we will look for solvability condition for it.
As we confirmed in the preceding section, the input-output equation is denoted as (E − Λν)y = Λω. This set of simultaneous equations has a unique solution if and only if E − Λν is non-singular.
In the economics world, it is well-known that this matrix has a unique solution if and only if all principal minors of the matrix are positive.7
David
Hawkins
and
Herbert
Simon
, who clarified this condition,8 interpreted it as follows.
“The condition that all principal minors must be positive means, in economic terms, that the group of industries corresponding to each minor must be capable of supplying more than its own needs for the group of products produced by this group of industries.”9
However, there is an illogical leap between this economic interpretation and the mathematical condition which they derived. They did not clarify the mathematical validity of their interpretation. It is natural that
David
Gale
did not recognize any economic significance of this condition.10
There are people who have interpreted this condition using the concept of direct and indirect requirements. This interpretation was first shown by
Robert
Dorfman
,
Paul
Samuelson
and
Robert
Solow
,11 but a mathematical error was included in their interpretation. It was refined by Ki-Jun Jeong12 and although his reinterpretation has affected some people,13 it does not satisfy the author. Jeong used an infinite series expression of the inverse to justify his interpretation.14 Similarly, many economists use infinite series of the inverse for economic interpretation of the input-output equation. However, we assume that the relevant term is finite. It seems to be impossible to require infinite time within a finite term. Infinite series of the inverse is certainly a mathematical truth, but the author asserts that it does not have any economic meaning.
Some economists attached importance to a solvability condition that ∃y > 0 such that (E − Λν)y > 0.15 Since (E − Λν)y = Λω, this condition means λkΩk > 0 for ∀k ∈ N. By Equation (9), we can derive Ωk > 0 for ∀k ∈ N. That is, this condition means that all commodities have surplus. However, it is not guaranteed that such a situation occurs.
In fact, there is a solvability condition weaker than this. If our assumption that (E − Λν)y ≥ 0 where ∃y > 0 is satisfied, there exists the following necessary and sufficient condition for non-singularity of E − Λν.
Let F be a subset of the relevant society N which is not empty and G be the complement of F if F is a proper subset. The condition is ∃k ∈ F such that λkΩk > 0 or ∃k ∈ F, ∃j ∈ G such that −λkνkj < 0 for ∀F ⊆ N.16 Considering Equations (3), (9) and (11), this condition can be rewritten as follows.
Theorem 3.1 Let F be a subset of the relevant society N which is not empty and G be the complement of F if F is a proper subset. The economic input-output equation has a unique solution if and only if ∃k ∈ F such that Ωk > 0 or ∃k ∈ F, ∃j ∈ G such that Zkj > 0 for ∀F ⊆ N.17
We will interpret this solvability condition.
“∃k ∈ F such that Ωk >
0”
expresses the fact that a part of the relevant society possesses a commodity which is not inputted in the relevant space-time. Moreover, “∃k ∈ F, ∃j ∈ G such that Zkj >
0”
expresses the fact that a part of the relevant society possesses a commodity which is inputted outside of there. Unifying both, these conditions means that commodities which a part of the relevant society possesses are not all inputted to its inside. In other words, they represent the fact that each part of the relevant society is open for its outside.
Hence, Theorem 3.1 insists that the input-output equation has a unique solution if and only if each part of the relevant society is open for its outside. We call this solvability condition the space-time openness of the economic input-output relation.
The space-time openness condition resembles the interpretation by
Hawkins
and
Simon
, but our derivation is logically more rigorous and obvious. Moreover, this condition seems to be relevant to the bounded confidence condition in the literature of social opinion evolution.18
Then, is the openness condition always true? Directly, it is not self-evident. However, the space-time openness is always true under an ordinary premise about time. In order to clarify this, we will examine the temporal structure of the input-output relation.
We divide the relevant term into several subterms. Dividing it into t subterms, we denote the relevant term by![]() . However, we set the index of subterms such that a smaller index corresponds to an earlier subterm and a larger index corresponds to a later subterm.
. However, we set the index of subterms such that a smaller index corresponds to an earlier subterm and a larger index corresponds to a later subterm.
Let Xi(u) be the gross input quantity of Sector i in Subterm u, and Yj(u) be the output quantity of Sector j in Subterm u, and Zij(u) be the separate input quantity from Sector i to Sector j in Subterm u.
As per Equation (2), each input and output in each subterm is all non-negative by their economic meanings.
![]() (16)
(16)
The next relation exists between the whole quantities in the relevant term and separate quantities in each subterm.
![]()
Gross input quantity in Subterm u is defined as the sum of separate input quantities from Sector i in Subterm u. Therefore,
![]() (17)
(17)
is satisfied between Zij(u) and Xi(u).
Then, what kind of relationship exists between Zij(u) and Yj(u)? We want to think that Yj(u) > 0 is accompanied by Zij(u) > 0 because input is defined as a use of a commodity which contributes to the production of a commodity, but this cannot be justified simply. Output may not occur in the subterm when input occurs. Hence, Yj(u) = 0 can be true even if Zij(u) > 0.
Here, we will reconsider when the input time and the output time are.
There is no room to argue when the output time is. The output time is when the commodity comes into existence from nothing. The problem is the input time. When is the input time? There may be someone who insists that it is the time the input commodity is used, but this paper defines it as a time that output to which input contributes is realized.19 Input is defined as the use of commodity which contributes to the production of the commodity. Therefore, the time when input is realized should be regarded as when the output to which it contributes is realized.
Under such a definition, it is a grammatical truth that input and output occur at the same time. We call this the realization simultaneity principle between input and output. Hereby, the next theorem is derived.
Theorem 3.2 “![]() ” and “
” and “![]() ” hold for
” hold for![]() .20
.20
Proof. The former proposition is justified by the definition of input and the realization simultaneity principle. The latter proposition is derived from the contraposition of the former proposition considering with Equation (16). [Q. E. D.]
The input-output table in Subterm u is as follows.
Then, let ρk(pq) be the circular disposal quantity which Sector k disposed from output in Subterm p to input in Subterm q. Let αk(q) be the disposal quantity which Sector k disposed from carried to input in Subterm q. Let βk(p) be the quantity which Sector k disposed from output in Subterm p to surplus. As per Equation (5), they are all non-negative.
![]() (18)
(18)
The disposal table of Sector k considering term division is as follows.
Note that, based on our common sense about time, a future fact cannot have an effect on any past fact. Moreover, a fact cannot have an effect on another fact which occurs at exactly the same time. Considering these, a fact can have an effect only from the past to the future.
If we apply a similar principle to the economic input-output relation, a commodity produced at a certain time can only contribute to only production in the future of the time. Note that we defined the input time as the time that the output to which the input contributes is realized. Thus, the preceding principle can be expressed that a commodity can be disposed only from the output of the past to the input of the future. We call this the disposal irreversibility principle.
We now think about the relationship between the disposal irreversibility principle and circular disposal quantities.
Based on the disposal irreversibility principle, circular quantities from the future to the past are naturally zeroes. Then, we think about the sign of simultaneous circular quantities. Based on Equation (18), it is always non-negative. However, we cannot judge whether it is positive or zero generally. For example, if subterms are divided monthly, output in a certain month may be or may not be inputted in the same month. If they are divided weekly or daily, a similar situation occurs.
However, the output time and the input time of one disposal are not exactly the same time by the disposal irreversibility principle. Hence, we can divide the relevant term between both times. Then, they belong to different subterms. If the number of disposals in the relevant term is finite m,21 each output time and input time of all disposals belong to different subterms by at most a finite m times division. If we define a subterm whose simultaneous circular quantities are zeroes for any sector as a basic-term, this fact means that the relevant term can always be divided into finite basic-terms.
These conclusions are summarized as follows.
Theorem 3.3 Under the premise of the disposal irreversibility principle, ρk(pq) = 0 holds for ∀k ∈ N, ∀p > q. Furthermore, the relevant term can always be divided into a finite number of basic-terms where a basic-term refers to a Subterm u such that ρk(uu) = 0 for ∀k ∈ N.
Based on Theorem3.3, we can prove that the space-time openness condition is guaranteed by the disposal irreversibility principle.
Theorem 3.4 Under the premise of the disposal irreversibility principle, ∃k ∈ F such that Ωk > 0 or ∃k ∈ F, ∃j ∈ G such that Zkj > 0 for ∀F ⊆ N.
Proof. It is enough to prove ∃k ∈ F such that Ωk > 0 if Zij = 0 for ∀i ∈ F, ∀j ∈ G. Based on Theorem 3.3, we divide the relevant term into finite basic-terms. Due to Equation (3), all sectors produce commodities in some basic-terms. Let Sector k ∈ F be the sector which produces last in F. Let Subterm u be a basic-term when Sector k produces last.22
First, we will prove the case u is not the first or the last basic-term.
Let Subterm− be the set of basic-terms which are before Subterm u, and Subterm+ be the set of basic-terms which are after Subterm u. In this case, the disposal table of Sector k is as follows.
By Theorem 3.3, ρk(u−) = 0, ρk(+−) = 0 and ρk(+u) = 0 are satisfied. Moreover, ρk(uu) = 0 is also satisfied because Subterm u is a basic-term, and Yk(u) > 0 because u is defined as the last basic-term whose output of k is positive. We put these facts in the disposal table.
Next, we will prove Xk(+) = 0 by dividing it into two cases.
1) The case F = N.
Subterm u is the last basic-term whose output in F = N is positive, and Subterm+ is after u. Thus, ∀Yj(+) = 0. Hence, ∀Zij(+) = 0 for ∀i, j ∈ N by Theorem 3.2. Then, ∀Xi(+) = 0 from Equation (17). Therefore, Xk(+) = 0.
2) The case F ⊊ N.
We write the input-output table of Subterm+ divided into F and G.
Subterm u is the last basic-term whose output in F is positive and Subterm+ is after u. Hence,
![]() . Moreover,
. Moreover, ![]() from the premise Zij = 0 for ∀i ∈ F, ∀j ∈ G. We put these facts
from the premise Zij = 0 for ∀i ∈ F, ∀j ∈ G. We put these facts
in the preceding input-output table.
Here, we focus on the column of Set F. From the latter proposition of Theorem 3.2, the elements of this column are all zeroes. We put these facts in the preceding input-output table.
Next, we focus on the row of Set F. We can see that![]() . As k belongs to F, Xk(+) = 0 is derived.
. As k belongs to F, Xk(+) = 0 is derived.
Now, we have confirmed that Xk(+) = 0 is satisfied generally. We add this fact to the preceding disposal table of k to obtain the following.
Now, we focus on the column of Subterm+. Since all disposal quantities are non-negative by Equation (18), all elements of this column are zeroes. We add this fact to the preceding disposal table of k to obtain the following.
Next, we focus on the row of Subterm u. We can see that βk(u) > 0. We add this fact to the preceding disposal table of k to obtain the following.
Then, we focus on the surplus column. As all disposal quantities are non-negative, we obtain Ωk > 0. The proof in the case u is not the first or the last basic-term is complete.
In the case u is the first basic-term; you should assume the row and column of Subterm− do not exist. In the case u is the last basic-term; you should assume the row and column of Subterm+ do not exist. Then, imitating the previous proof, you can easily prove Ωk > 0. [Q. E. D.]
From Theorems 3.1 and 3.4, we obtain the following theorem about the solvability of the economic input- output equation.
Theorem 3.5 Under the premise of the disposal irreversibility principle, the economic input-output equation has a unique solution.
This theorem shows that the solvability of the input-output equation indicates the feasibility of productive structure under time irreversibility. If a combination of the self-sufficiency rate and the input coefficient does not satisfy a solvability condition, the economic input-output structure is never realized as a time irreversible process.
Each input coefficient is decided by the technology to produce each commodity basically. Hence, if they are combined simply, a solvability condition may not be satisfied. Even if people try to execute their production planning under such a situation, contradiction must occur for the plan and it cannot be executed. The feasibility of a productive structure does not only depend on each production technology, but also on the total consistency of the productive structure under time irreversibility.
However, even if a combination of input coefficients cannot be realized, it may be realized in the case that the self-sufficiency rate can be regulated to satisfy the solvability condition.
4. Relationship between the Grandfather Paradox and the Solvability of the Economic Input-Output Equation
As shown in the preceding section, the economic input-output equation has always a unique solution if the economic input-output relation is a time irreversible process. This conclusion is similar to the grandfather paradox which is known as a type of time paradox.23
The grandfather paradox is an absurd situation which may occur if we suppose that time travel into the past is possible. Under such a supposition, a traveler into the past can murder his grandfather before his birth. However, if this comes true, he cannot be born. As a result he cannot murder his grandfather, contradicting the supposition.
When we think about the grandfather paradox, we must note that past travel does not always cause contradiction. It is not inevitable that the past traveler kills his grandfather. Nevertheless, why is killing emphasized as a paradox?
It may be because a situation where past travel is possible is compared with a situation in which it is impossible. If past travel is possible, the possibility of contradiction is not eliminated. That is, time reversibility is not a sufficient condition for avoiding contradiction. On the other hand, if it is impossible, no one can kill his grandfather before his birth, so the possibility of contradiction is eliminated. That is, time irreversibility is a sufficient condition for avoiding contradiction. As we can understand that contradiction does not always occur in case of past travel, it is not a necessary condition. However, it is certainly a sufficient condition. Since we are used to the irreversible world where contradiction does not occur, a paradoxical situation brought in the reversible world makes a strong impression on us.
The essence of the grandfather paradox can be summarized as follows. Time irreversibility is a sufficient condition for avoiding contradiction, but time reversibility is not. However, time irreversibility is not a necessary condition for avoiding contradiction.
On the other hand, as we have proved in this paper, the space-time openness condition is a necessary and sufficient condition for solvability of the economic input-output equation, and the disposal irreversibility principle is sufficient to open the space-time. However, we have not proved that it is necessary. The possibility of the space-time openness under a time reversible situation is not eliminated.
That is, time irreversibility is a sufficient condition for avoiding insolubility in the equation, but time reversibility is not. However, time irreversibility is not a necessary condition for avoiding insolubility.
If we replace the word “insolubility” with “contradiction”, the solvability of the input-output equation shares the same peculiarities with the grandfather paradox. Needless to say, contradiction and insolubility do not mean the same thing, but both are common with respect to the impossibility of normal recognition. That is, both the grandfather paradox and the solvability of the input-output equation refer to the following truth.
Time irreversibility is a sufficient condition for avoiding abnormal recognition, but time reversibility is not. However, time irreversibility is not a necessary condition for avoiding abnormal recognition.
Trustworthy evidence that time travel into the past is possible has never been shown until now. The grandfather paradox and the solvability of the input-output equation may be disadvantageous to the insistence that past travel is possible, but they do not become decisive evidence for the impossibility of past travel because they are not necessary conditions for normal recognition. I do not intend to judge the possibility of past travel which is a great problem about the basis of our world.24
However, if past travel is impossible, normal recognition is certainly guaranteed. I think that the significance of the grandfather paradox is not to insist that time reversibility brings a paradoxical situation, but to insist that time irreversibility guarantees normal recognition. Our usual recognitions adapt themselves to an irreversible environment without awareness. Together with the grandfather paradox, the solvability of the economic input- output equation clarifies an epistemological value of time irreversibility.
NOTES
1Cf.
Leontief
[1] pp. 33-34.
![]()
2We regard measures with the same quantitative units as an equivalent condition for the commodities being the same kind.
![]()
3Surplus in this paper corresponds to final demand in usual input-output analysis. However, surplus is not limited to what is demanded by a consumer. Commodities which exist but are not inputted in the relevant space-time are all involved in surplus even if not demanded by anyone.
![]()
4This definition of the self-sufficient rate resembles that of the import coefficient devised by the Japanese authorities (Cf. Administrative Management Agency and others [2] ). This import coefficient is defined as the import quantity per the sum of input and final demand. The number resulting from subtracting the import coefficient from 1 roughly corresponds to the self-sufficiency rate in this paper, but they are not exactly the same. The peculiarity of the Japanese authority model is that export is eliminated from the denominator of the import coefficient (Cf. Administrative Management Agency and others [2] p. 10). On the other hand, the denominator of our self-sufficiency rate is equal to Xk + Ωk from Equations (6) and (8), and export is included in Ωk.
5If we suppose![]() , this equation accords with the equation which
Leontief
first used (
Cf.
Leontief [1] pp. 34-41, Leontief [3] pp. 22-27). Referring to the definition of the self-sufficiency rate (Equation (8)), this is nothing but the situation that carried quantities are all zeroes.
, this equation accords with the equation which
Leontief
first used (
Cf.
Leontief [1] pp. 34-41, Leontief [3] pp. 22-27). Referring to the definition of the self-sufficiency rate (Equation (8)), this is nothing but the situation that carried quantities are all zeroes.
![]()
6Cf. Theorems 1.4 and
3.6 in
Miura [4] . E − Λν is an NPZ-matrix called in Miura [4] .
![]()
7Many economists may recognize this as a condition for the non-negativity of the inverse. However, as far as the positivity of output is premised as in this paper, it is also a non-singularity condition. Cf. Theorem
3.7 in
Miura [4] .
8 In
the economics world, this condition is often called the Hawkins-Simon condition because it is believed that this was first proved in
Hawkins
&
Simon
[5] published in 1949. However, it was already proved in Ostrowski [6] published in 1937. Cf. Berman & Plemmons [7] p. 161, Plemmons [8] p. 182. Moreover, it seems that
Maurice
Petron
anticipated this condition in 1913.
Cf.
Bidard
[9] pp. 57-58, Mori [10] p. 525.
9Cf. Hawkins & Simon [5] p. 248.
10He said, “This fact, however, gives us no new economic insight into the properties of
Leontief
models because there is no economic interpretation to be attached to these principal minors.” (
Gale
[11] preface x, footnote1).
11Cf. Dorfman & Samuelson &
Solow
[12] p. 215.
12Cf. Jeong [13] , [14] .
13For example,
Cf.
Fujita
[15] , Dasgupta [16] , Gim & Kim [17] , Fujita [18] .
14Jeong has shown that direct and indirect requirements can be formalized without using infinite series. However, in such a case, the meaning of an indirect requirement seems to be indistinct because the inverse of a minor is used just as it is.
15For example,
Cf.
Gale
[11] preface x, Morishima [19] p. 22, Nikaido [20] p. 12, p. 18.
16Cf. Theorem
3.12 in
Miura [4] . The prototype of this condition was first shown in Beauwens [21] and
Neumann
[22] .
17 In
the case F = N, this condition is merely ∃k Î F such that Ωk > 0.
![]()
18The recent works regarding this topic are Varshney [23] ,
Shang
[24] ,
Shang
[25] .
19This definition of the input time is now explained using a concrete example. We suppose that a winter wheat is planted in September 2014 and harvested in July 2015. If the relevant term is set 2014, the planted wheat is not recorded as an input because its input time is not September 2014 but July 2015. It is recorded as a surplus.
20“⟹” means logical implication.
![]()
21Since the finiteness of the relevant term is assumed, the number of disposals which can be justified empirically is only a finite number.
22As the relevant term is divided into finite basic-terms, the existence of the last basic-term is always guaranteed.
![]()
23The grandfather paradox is discussed in various places, including Oaklander [26] p. 4.
![]()
24However, I do not know whether a trustworthy sufficient condition for normal recognition which is alternative to time irreversibility can be found.