1. Introduction
The early 1970’s witnessed Bayesian inference going nonparametric with the introduction of statistical models with infinite dimensional parameter spaces. The most conspicuous of these models is the Dirichlet process [1] , which is a prior on the class of all probability measures over a given sample space that trades great analytical tractability for a reduced support: as shown by Blackwell [2] , its realizations are, almost surely, discrete probability measures. The posterior expectation of a Dirichlet process is a probability measure that gives positive mass to each observed value in the sample, making the plain Dirichlet process unsuitable to handle inferential problems such as density estimation. Many extensions and alternatives to the Dirichlet process have been proposed [3] .
In this paper we construct a prior distribution over the class of densities with respect to Lebesgue measure. Given a partition in subintervals of a bounded interval of the real line, we define a random density whose realizations have a constant value on each subinterval of the partition. The distribution of the values of the random density on each subinterval is specified by transforming and conditioning a multivariate normal distribution.
Our simple random density is the finite dimensional analogue of the stochastic processes introduced by Thorburn [4] and Lenk [5] . Computations with these stochastic processes involve an intractable normalization constant, and are restricted to values of the random density on a finite number of arbitrarily chosen domain points, demanding some kind of interpolation of the results. The finite dimensionality of our random density makes our computations more direct and transparent and gives us simpler statements and proofs.
An outline of the paper is as follows. In Section 2, we give the formal definition of a simple random density. In Section 3, we prove that the distribution of a simple random density is closed under sampling. The results of the simulations in Section 4 depict the asymptotic behavior of the posterior distribution. We extend the model hierarchically in Section 5 to deal with random partitions. Although the usual Bayes estimate of a simple random density is a discontinuous density, in Section 6 we compute smooth estimates solving a decision problem in which the states of nature are realizations of the simple random density and the actions are smooth densities of a suitable class. Additional propositions and proofs of all the results in the paper are given in Section 7.
2. Simple Random Densities
Let  be the probability space from which we induce the distributions of all random objects considered in the paper. For some integer
be the probability space from which we induce the distributions of all random objects considered in the paper. For some integer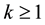 , let
, let  be the subset of vectors of
be the subset of vectors of 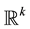 with positive components. Write
with positive components. Write 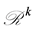 for the Borel sigma-field of
for the Borel sigma-field of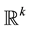 . Let
. Let  denote Lebesgue measure over
denote Lebesgue measure over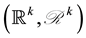 . We omit the indexes when
. We omit the indexes when . The components of a vector
. The components of a vector 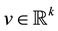 are written as
are written as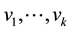 .
.
Suppose that we have been given an interval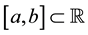 , and a set of real numbers
, and a set of real numbers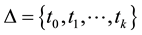 , such that
, such that , inducing a partition of
, inducing a partition of 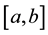 into the
into the 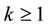 subintervals
subintervals
![]()
The class of simple densities with respect to this partition consists of the nonnegative simple functions which have a constant value on each subinterval and integrate to one. Let![]() , for
, for![]() , and define the map
, and define the map ![]() by
by![]() . Each simple density
. Each simple density ![]() within this class can be represented as
within this class can be represented as
![]()
in which ![]() is such that each
is such that each![]() , and
, and![]() . The
. The![]() ’s are the heights of the steps of the simple density f.
’s are the heights of the steps of the simple density f.
From now on, let![]() , for
, for![]() . Note that, by the definition of the
. Note that, by the definition of the![]() ’s given above, it follows that
’s given above, it follows that ![]() if
if![]() . Moreover, define the projection on the first
. Moreover, define the projection on the first ![]() coordinates
coordinates ![]() by
by![]() . For a normal random vector
. For a normal random vector ![]() with mean
with mean ![]() and
and ![]() covariance matrix
covariance matrix![]() , denote by
, denote by ![]() the distribution of the lognormal random vector
the distribution of the lognormal random vector![]() . If
. If ![]() is nonsingular, it is easy to show that U has a density
is nonsingular, it is easy to show that U has a density
![]()
in which ![]() is the determinant of
is the determinant of![]() , and we have introduced the notations
, and we have introduced the notations ![]() and
and![]() .
.
We define a random density whose realizations are simple densities with respect to the partition induced by ![]() specifying the distribution of the random vector of its steps heights. Informally, the steps heights will have the distribution of a lognormal random vector U given that
specifying the distribution of the random vector of its steps heights. Informally, the steps heights will have the distribution of a lognormal random vector U given that![]() . The formal definition of the random density is given in terms of a version of the conditional distribution of U given
. The formal definition of the random density is given in terms of a version of the conditional distribution of U given ![]() and the expression of its conditional density with respect to a dominating measure. However, we are outside the elementary case in which the joint distribution is dominated by a product measure. In fact, we have in Proposition 7.1 a simple proof that Lebesgue measure
and the expression of its conditional density with respect to a dominating measure. However, we are outside the elementary case in which the joint distribution is dominated by a product measure. In fact, we have in Proposition 7.1 a simple proof that Lebesgue measure ![]() and the joint distribution of U and
and the joint distribution of U and ![]() are mutually singular.
are mutually singular.
A suitable family of measures that dominate the conditional distribution of U given![]() , for each value of
, for each value of![]() , is described in the following lemma.
, is described in the following lemma.
Lemma 2.1. Let ![]() be defined by
be defined by![]() , for
, for![]() . Then, each
. Then, each ![]() is a measure over
is a measure over![]() .
.
The proof of Lemma 2.1 is given in Section 7. Figure 1 gives a simple geometric interpretation of the measures ![]() when the underlying partition is formed by three subintervals.
when the underlying partition is formed by three subintervals.
The following result is the basis for the formal definition of the random density.
Theorem 2.2. Let![]() , with nonsingular
, with nonsingular![]() , and let
, and let ![]() be the family of measures over
be the family of measures over ![]() defined on Lemma 2.1. Then, we have that
defined on Lemma 2.1. Then, we have that ![]() defined by
defined by
![]()
is a regular version of the conditional distribution of ![]() given
given![]() , in which
, in which
![]()
Moreover, ![]() , for each
, for each![]() .
.
The necessary lemmata and the proof of Theorem 2.2 are given in Section 7. The following definition of the random density uses the specific version of the conditional distribution constructed in Theorem 2.2.
Definition 2.3. Let![]() , with nonsingular
, with nonsingular![]() . We say that the map
. We say that the map ![]() defined by
defined by
![]()
is a simple random density, in which ![]() are the random heights of the steps of
are the random heights of the steps of![]() , with distribution given by
, with distribution given by![]() , for
, for![]() , and
, and ![]() is the regular version of the conditional distribution of U given
is the regular version of the conditional distribution of U given ![]() obtained in Theorem 2.2. Hence, for every
obtained in Theorem 2.2. Hence, for every![]() , we have
, we have
![]()
in which ![]() and it holds that
and it holds that![]() . We use the notation
. We use the notation![]() .
.
3. Conditional Model
Now, we model a set of absolutely continuous observables conditionally, given the value of a simple random density![]() . The following lemma, proved in Section 7, describes the conditional model and determines the form of the likelihood.
. The following lemma, proved in Section 7, describes the conditional model and determines the form of the likelihood.
Lemma 3.1. Consider ![]() represented as
represented as
![]()
and let the random variables ![]() be conditionally independent and identically distributed, given that
be conditionally independent and identically distributed, given that![]() , with distribution
, with distribution
![]()
in which we have defined![]() . Define
. Define ![]() and let
and let![]() .
.
Then, ![]() , almost surely
, almost surely![]() , with Radon-Nikodym derivative
, with Radon-Nikodym derivative
![]()
in which![]() , for
, for![]() .
.
The factorization criterion implies that ![]() is a sufficient statistic for
is a sufficient statistic for![]() . That is, in this conditional model, as one should expect, all the sample information is contained in the countings of how many sample points belong to each subinterval of the partition induced by
. That is, in this conditional model, as one should expect, all the sample information is contained in the countings of how many sample points belong to each subinterval of the partition induced by![]() .
.
Using the notation of Lemma 3.1, and defining![]() , we can prove that the prior distribution of
, we can prove that the prior distribution of ![]() is closed under sampling.
is closed under sampling.
Theorem 3.2. If![]() , then
, then![]() , in which
, in which![]() .
.
This result, proved in Section 7, makes the simulations of the prior and posterior distributions essentially the same, the only difference being the computation of![]() .
.
4. Stochastic Simulations
We summarize the distribution of a simple random density![]() , represented as
, represented as ![]() , in two ways. First, motivated by the fact, proved in Proposition 7.5, that the prior and posterior expectations are predictive densities, we take as an estimate the expectation of the steps heights
, in two ways. First, motivated by the fact, proved in Proposition 7.5, that the prior and posterior expectations are predictive densities, we take as an estimate the expectation of the steps heights![]() . Second, the uncertainty of this estimate is assessed defining
. Second, the uncertainty of this estimate is assessed defining
![]()
for![]() , and taking as a credible set the
, and taking as a credible set the ![]() with the smallest
with the smallest ![]() such that
such that![]() , in which
, in which ![]() is the credibility level.
is the credibility level.
The Random Walk Metropolis algorithm [6] is used to draw dependent realizations of the steps of ![]() as
as
values of a Markov chain![]() . The two summaries are computed through ergodic means of this chain. For
. The two summaries are computed through ergodic means of this chain. For
example, the credible set is determined with the help of the almost sure convergence of
![]()
As for the parameters appearing in Definition 2.3, we take in our experiments all the![]() ’s equal to one, and the covariance matrix
’s equal to one, and the covariance matrix ![]() is chosen in the following way. Given some positive definite covariance function
is chosen in the following way. Given some positive definite covariance function![]() , we induce
, we induce ![]() from C defining
from C defining
![]()
for![]() . In our examples we study the family of Gaussian covariance functions defined by
. In our examples we study the family of Gaussian covariance functions defined by ![]() , with dispersion parameter
, with dispersion parameter ![]() and scale parameter
and scale parameter![]() .
.
Example 4.1. Let ![]() and consider the sample space
and consider the sample space ![]() with
with![]() . For the sake of generality, we induce
. For the sake of generality, we induce ![]() from the family of Gaussian covariance functions with fixed dispersion parameter
from the family of Gaussian covariance functions with fixed dispersion parameter ![]() but with random scale parameter
but with random scale parameter![]() , in which
, in which![]() . These choices guarantee that computations with
. These choices guarantee that computations with ![]() are numerically stable. In Figure 2, the summaries of the prior distribution of
are numerically stable. In Figure 2, the summaries of the prior distribution of ![]() show that the value of
show that the value of ![]() controls the concentration of the prior. Fixing
controls the concentration of the prior. Fixing ![]() and generating data from the mixture
and generating data from the mixture
![]()
we have in Figure 3 the posterior summaries for different sample sizes. Note the concentration of the posterior as we increase the size of the samples.
![]()
Figure 2. Effect of the value of ρ0 on the concentration of the prior. The curves in black are prior expectations and the gray regions are credible sets with credibility level of 95%.
![]()
Figure 3. Posterior summaries for Example 4.1. On each graph, the black simple density is the estimate![]() , the light gray region is a credible set with credibility level of 95%, and the dark gray curve is the data generating density.
, the light gray region is a credible set with credibility level of 95%, and the dark gray curve is the data generating density.
We observe the same asymptotic behavior of the posterior distribution with data coming from a triangular distribution and a mixture of normals (with appropriate truncation of the sample space).
5. Random Partitions
Inferentially, we have a richer construction when the definition of the simple random density involves a random partition. Informally, we want a model for the random density in which the underlying partition adapts itself according to the information contained in the data.
We consider a family of uniform partitions of a given interval![]() . Each partition of this family will be described by a positive integer random variable K, which determines the number of subintervals in the partition. Since the parameter
. Each partition of this family will be described by a positive integer random variable K, which determines the number of subintervals in the partition. Since the parameter ![]() of the family of Gaussian covariance functions used to induce
of the family of Gaussian covariance functions used to induce ![]() may have different meanings for different partitions, we treat it as a positive random variable R.
may have different meanings for different partitions, we treat it as a positive random variable R.
Explicitly, we are considering the following hierarchical model: K and R are independent. Given that ![]() and
and![]() , we choose the uniform partition of the interval
, we choose the uniform partition of the interval ![]() induced by
induced by
![]()
induce ![]() from the family of Gaussian covariance functions, and take the simple random density
from the family of Gaussian covariance functions, and take the simple random density ![]() . Finally, the observables are modeled as in Lemma 3.1. This hierarchy is summarized in the following graph.
. Finally, the observables are modeled as in Lemma 3.1. This hierarchy is summarized in the following graph.
![]()
In the following example, instead of specifying priors for K and R, we define the likelihood of K and R by![]() , whose form is obtained in Proposition 7.6, find the maximum
, whose form is obtained in Proposition 7.6, find the maximum
![]() , and use these values in the definitions of the prior, determining the posterior summaries as we did in Section 4.
, and use these values in the definitions of the prior, determining the posterior summaries as we did in Section 4.
Example 5.1. With a sample of size 2000 generated from a ![]() distribution, we find the maximum of the likelihood of K and R at
distribution, we find the maximum of the likelihood of K and R at![]() . In Figure 4 we have the posterior summaries obtained using these values in the definition of the prior. Moreover, in the left graph of Figure 5 we have the distribution function
. In Figure 4 we have the posterior summaries obtained using these values in the definition of the prior. Moreover, in the left graph of Figure 5 we have the distribution function ![]() corresponding to the estimated posterior density. For the sake of comparison, we plot in the right graph of Figure 5 some quantiles of this distribution
corresponding to the estimated posterior density. For the sake of comparison, we plot in the right graph of Figure 5 some quantiles of this distribution ![]() against the quantiles of the distribution
against the quantiles of the distribution ![]() from which we generated the data.
from which we generated the data.
6. Smooth Estimates
It is possible to go beyond the discontinuous densities obtained as estimates in the last two sections and get smooth estimates of a simple random density ![]() solving a Bayesian decision problem in which the states of nature are the realizations of
solving a Bayesian decision problem in which the states of nature are the realizations of ![]() and the actions are smooth densities of a suitable class.
and the actions are smooth densities of a suitable class.
In view of Theorem 3.2, it is enough to consider the problem without data. As before, the sample space is the interval![]() , which is partitioned according to some
, which is partitioned according to some![]() . For a density f with respect to Lebesgue measure, we
. For a density f with respect to Lebesgue measure, we
denote its ![]() norm by
norm by![]() .
.
Proposition 6.1. For![]() , let
, let ![]() be densities with respect to Lebesgue measure, with support
be densities with respect to Lebesgue measure, with support![]() , such that
, such that![]() , and let
, and let ![]() be the class of densities of the form
be the class of densities of the form![]() , with
, with![]() , for
, for
![]()
Figure 4. Posterior summaries for Example 5.1. The black simple density is the estimate![]() , the light gray region is a credible set with credibility 95%, and the dark gray curve is the data generating density.
, the light gray region is a credible set with credibility 95%, and the dark gray curve is the data generating density.
![]()
Figure 5. Example 5.1. On the left graph, the black curve is the estimated distribution function ![]() and the gray curve is the data generating distribution function F0. On the right graph, we have the comparison of some of the quantiles of
and the gray curve is the data generating distribution function F0. On the right graph, we have the comparison of some of the quantiles of ![]() and F0.
and F0.
![]() , and
, and![]() . Let
. Let ![]() and define
and define ![]() as the class of densities which are realizations of
as the class of densities which are realizations of![]() . Define the loss function
. Define the loss function ![]() by
by
![]()
Then, the Bayes decision is![]() , in which
, in which ![]() minimize globally the quadratic form
minimize globally the quadratic form
![]()
subject to the constraints![]() , for
, for![]() , and
, and![]() , with the definitions
, with the definitions
![]()
![]()
We use the result of Proposition 6.1, proved in Section 7, choosing the![]() ’s inside a class of smooth densities that serve approximately as a basis to represent any continuous density with the specified support.
’s inside a class of smooth densities that serve approximately as a basis to represent any continuous density with the specified support.
For the next example, suppose that the support of the densities is the interval![]() . Bernstein’s Theorem (see [7] , Theorem 6.2) states that the polynomial
. Bernstein’s Theorem (see [7] , Theorem 6.2) states that the polynomial
![]()
approximates uniformly any continuous function f defined on![]() , when
, when![]() . Suppose that f is a density. If we define, for
. Suppose that f is a density. If we define, for![]() ,
,
![]()
we can rewrite the approximating polynomial as![]() , in which
, in which ![]() is a density of a
is a density of a ![]() random variable. Hence, if we take a sufficiently large N, we expect that any continuous density with support
random variable. Hence, if we take a sufficiently large N, we expect that any continuous density with support ![]() will be reasonably approximated by a mixture of these
will be reasonably approximated by a mixture of these![]() ’s.
’s.
Example 6.2. Suppose that we have a sample of 5000 data points simulated from a truncated exponential distribution, whose density is
![]()
Repeating the analysis made in Example 5.1, we find the maximum of the likelihood of K and R at ![]() . The left graph of Figure 6 presents the posterior summaries. After that, we solved the problem of constrained optimization in Proposition 6.1 and found the results shown in the right graph of Figure 6.
. The left graph of Figure 6 presents the posterior summaries. After that, we solved the problem of constrained optimization in Proposition 6.1 and found the results shown in the right graph of Figure 6.
7. Additional Results and Proofs
In this section we present some subsidiary propositions and give proofs to all the results stated in the paper.
Proposition 7.1. Let ![]() and denote by
and denote by ![]() the joint distribution of
the joint distribution of ![]() and
and![]() . Then,
. Then,![]() .
.
Proof. Define the set![]() . Then,
. Then,
![]()
by definition of![]() . On the other hand, note that
. On the other hand, note that![]() , since this is the
, since this is the ![]() -volume of the k-di-
-volume of the k-di-
mensional hyperplane defined by the set A. Since![]() , the result follows.
, the result follows.
Proof of Lemma 2.1. When![]() , the result is trivial, since in this case
, the result is trivial, since in this case![]() , making
, making ![]() a null measure. Suppose that
a null measure. Suppose that ![]() and let
and let ![]() be the function defined by
be the function defined by
![]()
Define ![]() by
by![]() . We will show that
. We will show that![]() , for every
, for every![]() . Suppose that
. Suppose that![]() . Then, there is a
. Then, there is a ![]() such that
such that ![]() and
and
![]()
![]()
Figure 6. Example 6.2. On the right graph, the black simple density is the estimate![]() , and the light gray region is a credible set with credibility 95%. On both graphs the dark gray curve is the data generating density. On the left graph, the black smooth density is the Bayes decision of Proposition 6.1.
, and the light gray region is a credible set with credibility 95%. On both graphs the dark gray curve is the data generating density. On the left graph, the black smooth density is the Bayes decision of Proposition 6.1.
Since![]() , we have that
, we have that![]() , implying that
, implying that![]() . Since
. Since![]() , it follows from
, it follows from
the definition of the inverse image of ![]() that
that ![]() and, therefore, we conclude that
and, therefore, we conclude that ![]() . To prove the other inclusion, suppose that
. To prove the other inclusion, suppose that ![]() and define
and define![]() . Hence,
. Hence, ![]() and by the definition of
and by the definition of ![]() we have that
we have that
![]()
implying that![]() , because
, because![]() . Since
. Since ![]() and
and![]() , it follows that
, it follows that ![]() . Therefore,
. Therefore,![]() . Hence, we have that
. Hence, we have that ![]() and the properties of the inverse image of
and the properties of the inverse image of ![]() and the Lebesgue measure entail that each
and the Lebesgue measure entail that each ![]() is a measure over
is a measure over![]() .
.
Lemma 7.2. Let![]() . Let
. Let![]() , defined by
, defined by
![]()
be a measure over![]() . Denote by
. Denote by ![]() the joint distribution of
the joint distribution of ![]() and
and![]() . Then, we have that
. Then, we have that![]() , with Radon-Nikodym derivative
, with Radon-Nikodym derivative ![]() given by
given by
![]()
in which ![]() and
and![]() .
.
Proof. Define the function ![]() by
by![]() . Note that
. Note that![]() . Define the function
. Define the function ![]() by
by![]() , with
, with ![]() and
and![]() . The diagram
. The diagram
![]()
commutes, since![]() , for every
, for every![]() . For every
. For every![]() , we have that
, we have that
![]()
in which the fifth equality is obtained transforming by T, ![]() and
and![]() . It follows that
. It follows that![]() , and the Radon-Nikodym derivative has the desired expression.
, and the Radon-Nikodym derivative has the desired expression.
Lemma 7.3. Let ![]() be the measure defined on Lemma 7.2 and let
be the measure defined on Lemma 7.2 and let ![]() be the family of measures defined on Lemma 2.1. Then, for every measurable nonnegative
be the family of measures defined on Lemma 2.1. Then, for every measurable nonnegative![]() , we have that
, we have that
![]()
in which ![]() and
and![]() .
.
Proof. Define ![]() by
by![]() . Hence, f is a differentiable function whose inverse is the differentiable function g defined on Lemma 2.1. The value of the Jacobian on the point
. Hence, f is a differentiable function whose inverse is the differentiable function g defined on Lemma 2.1. The value of the Jacobian on the point ![]() is
is![]() . Let
. Let![]() ,
, ![]() ,
, ![]() , and define
, and define ![]() as in Lemma 2.1. When
as in Lemma 2.1. When![]() , we have already shown in the course of the proof of Lemma 2.1 that
, we have already shown in the course of the proof of Lemma 2.1 that![]() , for every
, for every![]() . Remembering
. Remembering
that, by definition, ![]() , it follows that
, it follows that ![]() and we conclude that
and we conclude that ![]()
![]() . Now suppose that
. Now suppose that![]() . In this case, since
. In this case, since![]() , we have that
, we have that![]() . As for the value of
. As for the value of![]() , consider two subcases: since
, consider two subcases: since
![]()
if any of the![]() , then
, then![]() , otherwise, we have
, otherwise, we have
![]()
and again it happens that![]() . Therefore, we conclude that in this case also
. Therefore, we conclude that in this case also
![]() . Hence, for
. Hence, for ![]() and
and![]() , we have that
, we have that
![]()
in which ![]() and
and![]() , the third equality is obtained transforming by f, and the penultimate equality is a consequence of Tonelli’s Theorem. The result follows from the Product Measure Theorem and Fubini’s Theorem (see [8] , Theorems 2.6.2 and 2.6.4).
, the third equality is obtained transforming by f, and the penultimate equality is a consequence of Tonelli’s Theorem. The result follows from the Product Measure Theorem and Fubini’s Theorem (see [8] , Theorems 2.6.2 and 2.6.4).
Lemma 7.4. Let![]() . Let
. Let ![]() be the family of measures defined on Lemma 2.1. Let
be the family of measures defined on Lemma 2.1. Let ![]() be the distribution of
be the distribution of![]() . Then,
. Then, ![]() with Radon-Nikodym derivative
with Radon-Nikodym derivative ![]() given by
given by
![]()
Proof. Let![]() ,
, ![]() , and
, and![]() . Let
. Let ![]() be the measure defined on Lemma 7.2. We have that
be the measure defined on Lemma 7.2. We have that
![]()
in which the penultimate equality follows from Lemma 7.2, and the last equality follows from Lemma 7.3. Hence, ![]() and the Radon-Nikodym derivative has the desired expression.
and the Radon-Nikodym derivative has the desired expression.
Proof of Theorem 2.2. Let ![]() be the joint distribution of
be the joint distribution of ![]() and
and![]() , and let
, and let ![]() be the distribution of
be the distribution of![]() . For
. For ![]() and
and![]() , by the definition of conditional distribution, we have that
, by the definition of conditional distribution, we have that
![]()
in which we have used the Leibniz rule for the Radon-Nikodym derivatives. On the other hand, by Lemmas 7.2 and 7.3, we have that
![]()
with ![]() and
and![]() . Both expressions for
. Both expressions for ![]() are compatible if
are compatible if
![]()
for almost every r![]() . Therefore, we have that
. Therefore, we have that![]() , for almost every
, for almost every ![]()
![]() , with Radon- Nikodym derivative
, with Radon- Nikodym derivative ![]() given by
given by
![]()
as desired. The fact that ![]() follows immediately.
follows immediately. ![]()
Proof of Lemma 3.1. Let ![]() be the measures over
be the measures over ![]() defined by
defined by![]() , for
, for
each![]() . Let
. Let![]() , with
, with![]() , for
, for![]() . By the hypothesis of conditional independence and Tonelli’s Theorem, we have that
. By the hypothesis of conditional independence and Tonelli’s Theorem, we have that
![]()
Hence, ![]() and
and ![]() agree on the
agree on the ![]() -system of product sets that generate
-system of product sets that generate![]() . Therefore, by Theorem A.26 of [9] , both measures agree on the whole sigma-field
. Therefore, by Theorem A.26 of [9] , both measures agree on the whole sigma-field![]() . It follows that
. It follows that![]() , almost surely
, almost surely![]() , and the Radon-Nikodym derivative has the desired expression.
, and the Radon-Nikodym derivative has the desired expression. ![]()
Proof of Theorem 3.2. By Bayes Theorem, for each![]() , we have that
, we have that
![]()
in which we have used the expression of the likelihood obtained in Lemma 3.1, the Leibniz rule for the Radon-Nikodym derivatives, the expression of ![]() in Definition 2.3, and the constant
in Definition 2.3, and the constant ![]() is such that
is such that![]() . The remainder of the proof relies on some matrix algebra. Let I be the identity matrix. Since,
. The remainder of the proof relies on some matrix algebra. Let I be the identity matrix. Since,
by definition, ![]() is symmetric , we have that
is symmetric , we have that![]() . Therefore, we have that
. Therefore, we have that
![]() . Write
. Write![]() . Since the scalar
. Since the scalar ![]() is equal to its transpose
is equal to its transpose![]() , we have that
, we have that
![]()
Defining![]() , we have
, we have
![]()
with![]() . Define
. Define![]() . Since the scalar
. Since the scalar
![]() , we have that
, we have that![]() . Hence, we obtain
. Hence, we obtain
![]()
Using this result in the expression of ![]() together with the expression of
together with the expression of![]() , we have
, we have
![]()
in which ![]() and
and ![]() is a density of the random vector
is a density of the random vector![]() . We conclude that, given that
. We conclude that, given that![]() , the vector H has the distribution of the heights of the steps of
, the vector H has the distribution of the heights of the steps of![]() , as desired.
, as desired.
Proposition 7.5. Suppose that the random variables ![]() are modeled according to Lemma 3.1. Denote by
are modeled according to Lemma 3.1. Denote by ![]() the distribution of
the distribution of![]() , for
, for![]() . For convenience, use the notations
. For convenience, use the notations ![]() and
and![]() . Then, for every
. Then, for every![]() , we have
, we have
1)![]() , for
, for![]() ;
;
2)![]() , a.s.
, a.s.![]() .
.
Proof. By Definition 2.3, we have
![]()
in which ![]() and
and![]() , for
, for![]() . In an analogous manner, we have
. In an analogous manner, we have
![]()
For item 1), note that
![]()
in which the fourth equality follows from Tonelli’s Theorem. For item 2), for each![]() , we have
, we have
![]()
On the other hand, we have
![]()
in which the third equality follows from the hypothesis of conditional independence and Theorem B.61 of [9] , the fourth equality is a consequence of Theorem 2.6.4 of [8] , and the sixth equality is due to Tonelli’s Theorem. Comparing both expressions for![]() , we get the desired result.
, we get the desired result.
Proposition 7.6. Let ![]() over
over ![]() be the distribution of K and let
be the distribution of K and let ![]() over
over ![]() be the distribution of R. Denote by
be the distribution of R. Denote by ![]() the joint distribution of K and R, which by the independence of K and R is equal to the product measure
the joint distribution of K and R, which by the independence of K and R is equal to the product measure![]() , and let
, and let ![]() be the joint distribution of K, R and H. In the hierarchical model described in Section 5, we have that
be the joint distribution of K, R and H. In the hierarchical model described in Section 5, we have that![]() , almost surely
, almost surely![]() , with Radon-Nikodym derivative
, with Radon-Nikodym derivative
![]()
for the ![]() defined on Lemma 3.1.
defined on Lemma 3.1.
Proof. Let ![]() and
and![]() . By the definition of conditional distribution, we have
. By the definition of conditional distribution, we have
![]()
On the other hand, by arguments similar to those used in the proof of Proposition 7.5, we have
![]()
Comparing both expressions for![]() , we have
, we have
![]()
almost surely![]() , and the result follows.
, and the result follows. ![]()
Proof of Proposition 6.1. By Tonelli’s Theorem, the expected loss is
![]()
in which we have defined the positive constant![]() . By hypothesis, each
. By hypothesis, each ![]() has the form
has the form![]() , leading us to
, leading us to
![]()
in which we have used the linearity of the integral. Therefore, minimizing the expected loss is the same as solving the problem of constrained minimization of the quadratic form Q. For the matrix![]() , note that, for every non null
, note that, for every non null![]() , we have
, we have
![]()
in which we have used the linearity of the integral. Therefore, the matrix M is positive definite, yielding (see [10] ) that the quadratic form Q is convex and the problem of constrained minimization of Q has a single global solution![]() . Since the Bayes decision is the f that minimizes the expected loss, the result follows.
. Since the Bayes decision is the f that minimizes the expected loss, the result follows.
8. Conclusion
The random density considered in the paper can be extended to multivariate problems introducing analogous partitions of d-dimensional Euclidean space. Also, as an alternative to the empirical approach used in Section 5, we can specify full priors for the hyperparameters. Although more computationally challenging, this choice defines a more flexible model with random dimension for which the density estimates are no longer simple densities. More general random partitions can also be considered.