The Solitary Waves Solutions of the Internal Wave Benjamin-Ono Equation ()
1. Introduction
Since the solitary wave was discovered in 1834, the researches on the nonlinear solitary wave propagation phenomena have been widely developed [1] . The internal solitary wave (ISW) is the nonlinear large amplitude wave existing in the ocean pycnocline. The ISWs have been observed by the synthetic aperture radar and on-site measurement in several ocean areas [2] . They have very great influence on the oceanic engineering, military and biology and so on. The research on the ISWs is a hot topic in the field of oceanology ( [3] and references therein). With regard to the different marine circumstances, the ISWs propagation can be described by different nonlinear differential equations [4] [5] . The study on the internal wave equations is an effective way for discussing the ISW propagation features [6] [7] . According to the depth of the interface where the ISWs occur, the governing equations can be divided into the shallow water and deep water internal wave models [8] [9] . The deep ocean area is very huge and there exists abundant resources. Nowadays, the offshore oil and gas resources have become less and less in most regions of the world. It is a trend to explore the deep ocean. The deep oceanic internal waves may bring very big influence to the exploitation of the deep ocean. Thus, the researches on the internal waves in the deep ocean deserve a lot.
One of the deep oceanic ISW equations is the Benjamin-Ono (BO) equation with the form
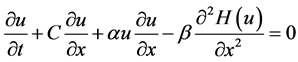 , (1)
, (1)
with .
. 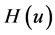 denotes the Hilbert transformation,
denotes the Hilbert transformation,
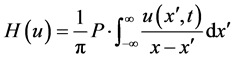
and the coefficients are
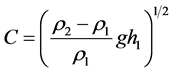 ,
,
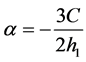 ,
,
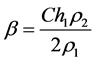 .
.
where 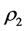 is the density of the lower fluid and
is the density of the lower fluid and 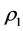 is that of the upper, and
is that of the upper, and  is the depth of the upper fluid. The BO equation is an integro-differential type equation which can describe the internal wave propagation in a deep stratified fluid [10] - [12] . It can also describe the mesoscale motion in the atmosphere if the meridional disturbance wind is weak [13] . Without the linear velocity term, the BO type equation has been investigated theoretically and numerically [14] - [16] . To our knowledge, the mutli-solitary wave solutions for Equation (1) have not been given. In soliton theory, there are many analytical methods for solving the nonlinear differential equations, among which the bilinear method is one direct and efficient way for obtaining the multi-solitary wave solutions [17] - [19] . In this paper, we will derive the multi-solitary wave solutions analytically for Equation (1) using the bilinear method and discuss the propagation and interaction features based on the obtained analytic results.
is the depth of the upper fluid. The BO equation is an integro-differential type equation which can describe the internal wave propagation in a deep stratified fluid [10] - [12] . It can also describe the mesoscale motion in the atmosphere if the meridional disturbance wind is weak [13] . Without the linear velocity term, the BO type equation has been investigated theoretically and numerically [14] - [16] . To our knowledge, the mutli-solitary wave solutions for Equation (1) have not been given. In soliton theory, there are many analytical methods for solving the nonlinear differential equations, among which the bilinear method is one direct and efficient way for obtaining the multi-solitary wave solutions [17] - [19] . In this paper, we will derive the multi-solitary wave solutions analytically for Equation (1) using the bilinear method and discuss the propagation and interaction features based on the obtained analytic results.
This paper will be organized as following. In Section 2, the multi-solitary wave solutions for the BO equation will be presented. In Section 3, the propagation analysis for the multi-solitary waves will be given. And then, the last section will be the conclusion.
2. Multi Internal Solitary Waves Solutions
Firstly, the BO Equation (1) is bilinearized under the dependent variable transformation
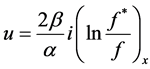 , (2)
, (2)
with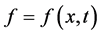 . Substituting the transformation into Equation (1), we can obtain
. Substituting the transformation into Equation (1), we can obtain
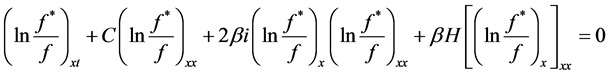 , (3)
, (3)
Integrating once in both sides with respect to 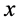 and choosing the integration constant to be zero, Equation (3) becomes
and choosing the integration constant to be zero, Equation (3) becomes
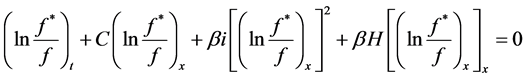 . (4)
. (4)
According to Ref. [12] , the BO Equation (1) has the algebraic one-solitary solution as below,
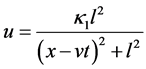 , (5)
, (5)
with the nonlinear phase speed
![]() ,
,
and characteristic half width of the soliton
![]() .
.
We can rewrite the solution (5) as the following form,
![]() ,
,
![]() (6)
(6)
with
![]() . (7)
. (7)
According to the procedure presented by Matsuno [14] for BO equation without linear velocity term, the internal wave BO Equation (1) including linear velocity term can be transformed to be the bilinear form
![]() , (8)
, (8)
where ![]() and
and ![]() are the bilinear derivative operators [20] defined as,
are the bilinear derivative operators [20] defined as,
![]() .
.
Based on the bilinear Equation (8) and using the bilinear method, the N-solitary wave solution for Equation (1) is given in the matrix form,
![]() , (9)
, (9)
whose entries are,
![]() (10)
(10)
with
![]() (11)
(11)
For![]() , the solution given by expression (9) agrees with the solution (5). For the two-solitary wave solution,
, the solution given by expression (9) agrees with the solution (5). For the two-solitary wave solution, ![]() is in the following form
is in the following form
![]() , (12)
, (12)
with
![]() (13)
(13)
3. Solitary Wave Propagation and Interaction
Using the multi-solitary wave solutions given by solution (9), different kinds of multi-solitary wave interactions can be figured and observed. In this section, based on the obtained exact solutions of the BO equation, the propagation and interaction for the internal solitary waves will be given and discussed. The hydrographic parameters are given as: the depth is above 2000 m. The pycnocline depth can be given as![]() . The upper den-
. The upper den-
sity![]() , the lower is
, the lower is ![]() and the density difference is
and the density difference is![]() .
.
Figure 1 plots the descent one-solitary wave propagation. Using the two-solitary wave solution, we can discuss two solitons interaction. In Figure 2, two solitons propagate parallel with ![]() and
and![]() . We can see that the soliton with large amplitude locates before the one with the small amplitude. The larger soliton is with the velocity of
. We can see that the soliton with large amplitude locates before the one with the small amplitude. The larger soliton is with the velocity of ![]() and the smaller one with
and the smaller one with![]() , so that the larger soliton will propagate faster than the smaller one. And the two solitons propagate without interaction. In Figure 3, we can see two oblique solitons interaction with
, so that the larger soliton will propagate faster than the smaller one. And the two solitons propagate without interaction. In Figure 3, we can see two oblique solitons interaction with ![]() and
and![]() . From Figure 3, the soliton with the larger amplitude meets the one with the small amplitude and interaction happens, and then they remain the shapes of each other after interaction.
. From Figure 3, the soliton with the larger amplitude meets the one with the small amplitude and interaction happens, and then they remain the shapes of each other after interaction.
4. Conclusion
In this paper, the multi-solitary wave solutions of the Benjamin-Ono equation which can describe the internal
![]()
Figure 1. The one-solitary wave propagation plot with amplitude 40 m.
![]()
![]() (a) (b)
(a) (b)
Figure 2. (a) Two parallel solitons; (b) The sectional plots of two parallel solitons interaction at different times.
![]()
![]() (a) (b)
(a) (b)
Figure 3. (a) The contour plot of two oblique solitons; (b) The sectional plots of two oblique solitons interaction at different times.
wave propagation in the deep ocean are given. Using the obtained analytic solutions, we have discussed the one- and two-solitary internal wave propagation and interaction. With different amplitudes, the different kinds of interactions of solitons may happen. It is hoped that the analytic results obtained in this paper is helpful for further study on the deep ocean internal waves.
Acknowledgements
This work has been supported by Beijing Excellent Talent Training Project (2013D005007000003), the Scientific Research Project of Beijing Educational Committee (No. SQKM201211232016) and the National Natural Science Foundation of China under Grant No. 61072145.