Theoretical Model of Diffraction Line Profiles as Combinations of Gaussian and Cauchy Distributions ()
1. Introduction
Diffraction line profiles due to polycrystalline materials have long been recognized to be caused by physical parameters like sizes of and defects in constituent powder particles. For this purpose, parameters like full width at half maximum (FWHM) intensity, integral width of line profile, Fourier transforms of intensity profile etc. have been utilized. Additionally, the moments [1] [2] and cumulants [3] of the line profile have also been used. These methods include recording of the line profile and correcting them for various sources of errors prior to calculations. Therefore, it may be beneficial to develop a reasonable mathematical model for the sample, the profile and the process. Such models are also required for structure refining methods as in Reitveld refinement.
The author previously showed that line broadening in a diffraction intensity profile of powdered crystalline materials due to stacking fault can be characterized in terms of the Zeroth, the First, the Second, the Third, and the Fourth Moment and the Fourth Cumulant [4] . In the present article, the scope of the characterization has been expanded to include line broadening due to particle size and strain as well. An example of a model that includes these factors may be found using Cauchy and Gauss functions. When the size effect is more predominant, the function is found to be more Cauchy-like and when the effect of strain is predominant, the Gauss model preponderates. So, the ideal model would be a suitable combination of both.
The author has in the past described a method of differentiating between Cauchy and Gauss distributions in diffraction line profiles [5] . These distributions are now standard and are used by investigators all over the world to identify the characteristics of crystalline materials. The two distributions are given as follows:
1) Gauss distribution:
 (1)
(1)
2) Cauchy distribution:
 (2)
(2)
where f(x) is the distribution for the variable x. The author also showed that the cumulative distribution
 for these two distributions was provided in the past [5] as follows:
for these two distributions was provided in the past [5] as follows:
For Gauss distribution:
 (3)
(3)
For Cauchy distribution:
 (4)
(4)
Therefore, comparison of a graph of
 vs x with the calculated values of
vs x with the calculated values of
 and
and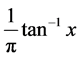 would determine the nature of the distribution, i.e., whether it is of a Cauchy or Gauss type. Using these criteria, a plot of
would determine the nature of the distribution, i.e., whether it is of a Cauchy or Gauss type. Using these criteria, a plot of
 vs
vs 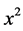
for a sample of Kaolinite, to test the formula

yielded the value of μ, the physical parameter describing the diffraction pattern, and revealed that the distribution in this case was of a Cauchy type [6] . On the other hand, if the material had a Gauss distribution, a plot of  vs
vs  would yield the value of μ. Hence the R(x) test can be used to distinguish between crystallites that are purely Gauss vs purely Cauchy.
would yield the value of μ. Hence the R(x) test can be used to distinguish between crystallites that are purely Gauss vs purely Cauchy.
2. Distributions for Convolution(s) of Gauss and Cauchy Functions
In actual practice, the distribution may be neither pure Gaussian nor pure Cauchy—but a combination of both. Several options are possible—1) a sum of partly Gaussian or partly Cauchy, 2) the convolution of partly Gaussian or partly Cauchy functions, 3) or even the same proportion of Gauss and Cauchy functions. These combinations may be purely additive or purely convolutional. The convolution may be of purely Gaussian and purely Cauchy (Voigt profile) [7] or partly Gaussian and partly Cauchy distributions (Pseudovoigt profiles) [8] . Therefore, the goal of the present effort was to identify criteria to distinguish between these various combinations. Since the convolutional combinations are likely to be the most abundant, here we shall concentrate on these criteria.
2.1. Voigt Functions
Convolution of two functions is by definition the inverse Fourier Transform of the product of the Fourier Transforms of the two functions i.e.
 (5)
(5)
where Fg is of the Fourier Transform of the function g and Fc is the Fourier Transform of the function c (F−1 is the inverse Fourier Transform of the product).
The Fourier Transform of 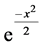 is
is  and Fourier Transform of
and Fourier Transform of , so the product of the Fourier Transform of the function
, so the product of the Fourier Transform of the function 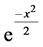 and
and  is
is
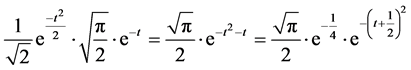 (6)
(6)
Since Fourier Transform carries a function in x space into t space while inverse Fourier Transform takes it back into x space,
 , using
, using 
Thus for convolutions representing the Voigt function:
 (7)
(7)
2.2. Pseudovoigt Functions
Pseudovoigt functions may be additive like η Cauchy + (1 − η) Gauss or of convolution type like
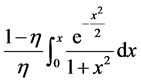
where η is called the mixing fraction, and can be used to denote the proportion of intensity of the Cauchy type.
3. Fourier Transform of Integral Width Explaining Why Particle Size and Strain Affect Diffraction Line Profile
3.1. Integral Width to Express Intensity Distribution in a Diffraction Profile
Although peak position, peak height, half intensity width etc. have been used to describe an intensity distribution in a diffraction profile, the first satisfactory parameter has been the integral width  where I(θ) is the intensity diffracted in the direction θ. For Voigt function the integral width will be
where I(θ) is the intensity diffracted in the direction θ. For Voigt function the integral width will be
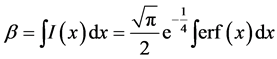 (7a)
(7a)
and for the Pseudovoigt function of the additive type, this can be described in terms of
 (7b)
(7b)
Whereas for the Pseudovoigt function of the convolution type,
 (7c)
(7c)
Langford introduced the Voigt function through the integral width [7] . Instead of considering the convolution of the Gauss and Cauchy functions he used the convolution of the expressions of integral width as functions of Gauss and Cauchy types—

Fourier Transform of  and
and 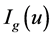 are given by
are given by
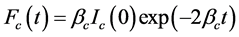
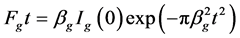

Thus
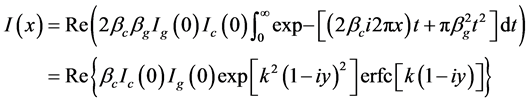
 is a complex error function defined by
is a complex error function defined by 
then 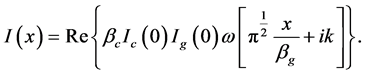
Integral width 
Ida [9] expressed the convolution in the form

where  is a scaled complex error function called the Faddeva Function.
is a scaled complex error function called the Faddeva Function.
3.2. Fourier Transform of Diffraction Profile Based on Integral Width
As mentioned in Section 2 above, Fourier Transform of 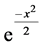 and
and 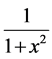 are
are  and
and  respectively.
respectively.
For Voigt function the Fourier Transform is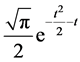 .
.
While the Fourier Transform for Pseudovoigt function of additive type is
 (7d)
(7d)
3.3. Moments of Diffraction Profiles Broadened by Particle Size and Strain
Intensity of X-ray diffracted in the direction , where θ is the angle of scattering and λ is the wave length of the radiation scattered, is given by
, where θ is the angle of scattering and λ is the wave length of the radiation scattered, is given by
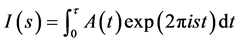 (8)
(8)
where τ is the limit where A(t) vanishes. By inverse Fourier Transform
 (9)
(9)
And so, 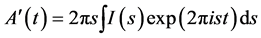 , and
, and
 (10)
(10)
By differentiating Equation (8) with respect to t over and over again and then assuming t = 0, we obtain the values of ,
,  etc.
etc.
Wilson has shown that [1] , the variance or the Second Moment of the diffraction profile can be given by
 (11)
(11)
where σ1 and σ2 are limits of the integral (8) instead of 0 to τ where A(t) vanishes. Very often σ1 = σ2.
The author [2] previously showed that the Fourth Moment of the intensity expression is given by
 (12)
(12)
In Equations (11) and (12), there are other terms involving  in Equation (11) and
in Equation (11) and  in Equation (12). But these terms are negligible compared to the remaining terms. The size of the particle comprising the powder is given by the 0th Moment of I(s) i.e.
in Equation (12). But these terms are negligible compared to the remaining terms. The size of the particle comprising the powder is given by the 0th Moment of I(s) i.e.
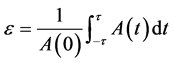 (13)
(13)
The Second and the Fourth Moment of the line profile yield the shape of the particles comprising the powdered sample. Of course, they and other moments yield information regarding crystal deformations due to strain, stacking faults, nature and the extent of dislocations etc. In Equations (11)-(13) we have used equations for particle size only, disregarding other factors like strain, dislocation density etc.
The author previously also showed that for a powder particle of size  and
and  with interfacial angles α, β and γ and Lattice constants a, b, c, the volume common to the crystal and its ghost removed by t in the hkl direction, is given by [6]
with interfacial angles α, β and γ and Lattice constants a, b, c, the volume common to the crystal and its ghost removed by t in the hkl direction, is given by [6]
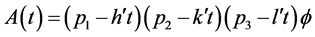
where  and
and , d is the interplanar spacing in the direction of diffraction and
, d is the interplanar spacing in the direction of diffraction and

where α, β and γ are angles between the axes Thus 
Therefore,



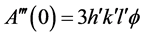
Hence
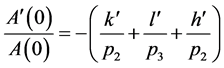


For h00, 0k0 and 00l reflection, only one dimension of the particle will be obtained, with hk0, 0kl and h0l reflections only two dimensions will be obtained. For a cylindrical crystal, the above equations will be modified in terms of equations derived by Langford and Louër [10] .
4. Moments of Different Distributions
4.1. The Gaussian Profile
It is known from Equation 509 [11] that
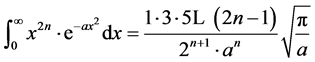 (14)
(14)
Putting n = 1 and a = 1/2, we have the expression for the Second Moment of a Gaussian function,
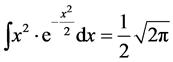 (15)
(15)
And putting n = 2 and a = 1/2, we have the expression for the Fourth Moment of a Gaussian function
 (16)
(16)
Equations (15) and (16) represent the Second and the Fourth Moment of a Gaussian profile. Cernansky has derived the equations [3]
 and
and  (16a)
(16a)
and
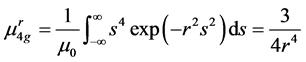
4.2. The Cauchy Profile
For a Cauchy profile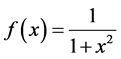 , the Second Moment, using Equation 67 [11] , is
, the Second Moment, using Equation 67 [11] , is
 (17)
(17)
and the Fourth Moment, from Equation 2.147.3 [10] , is
 (18)
(18)
4.3. The Voigt Profile
The Second Moment of the Voigt profile is given by
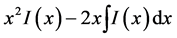 (19)
(19)
where  from Equation (7a)
from Equation (7a)
 from Equation 811 [11]
from Equation 811 [11]
 .
.
For large positive value of x
 from Equation 812 [11] .
from Equation 812 [11] .
Similarly the Fourth Moment of the Voigt profile is given by
 (20)
(20)
4.4. The Pseudovoigt Profile
For the Pseudovoigt profile of the convolution type the Second and Fourth Moment will be given by Equations
(19) and (20) multiplied by  and for Pseudovoigt profiles of additive type 1) Second Moment
and for Pseudovoigt profiles of additive type 1) Second Moment
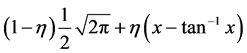 (21)
(21)
2) Fourth Moment
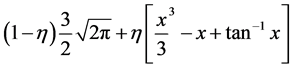 (22)
(22)
5. The Fourth Cumulant for the Different Distributions
Since the Second Moment and Second Cumulant are equal and we have already studied the Second Moment, we shall be examining only the Fourth Cumulant. All cumulants along with the Fourth Cumulant have the additive property namely

x1, x2, x3 being specific properties like size, strain, stacking fault, probability etc. The Fourth Cumulant C4 is given by
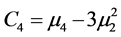
where μ4 and μ2 are the Fourth and Second Moment respectively which have been described in this paper. The Fourth Cumulant is given as shown below.
5.1. For Gaussian Distribution
Fourth Cumulant 
 by Equation (16)
by Equation (16)
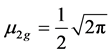 by Equation (15)
by Equation (15)
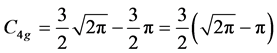 (23)
(23)
according to Cernansky  [3] . Indeed, Equations (22) and (23) indicate that it is a very small quantity.
[3] . Indeed, Equations (22) and (23) indicate that it is a very small quantity.
5.2. For Cauchy Distribution
By Equation (18) 
By Equation (17) 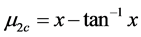
Thus
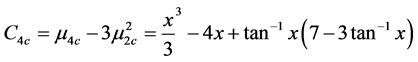 (24)
(24)
5.3. For Voigt Distribution
 from Equations (19) and (20).
from Equations (19) and (20).
5.4. For Pseudovoigt Distributions
The Fourth Cumulant can be found similarly from Equations (21) and (22). Now, to distinguish between Voigt and Pseudovoigt functions, an additional parameter, the coefficient of excess, is introduced here. It is the ratio of the Fourth Moment and three times the square of the Second Moment [12] . According to Cernansky for a Gaussian system the ratio is 1 [3] . The above calculations show that for the Cauchy system, the ratio is
 from Equations (18) and (17) respectively.
from Equations (18) and (17) respectively.
Hence this study proposes that Equations (19) and (21) may be used for identifying Voigt and Pseudovoigt distributions, respectively.
5.5. The χ Test
Pearson and Hartley [13] have described the χ test for determining the nature of the lineprofile. Here 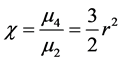 for Gaussian function and
for Gaussian function and 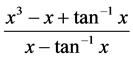 for Cauchy distribution.
for Cauchy distribution.
For Voigt and Pseudovoigt distribution Equations (20) and (19), (22) and (21) should be used.
6. Parameters from Either a Single or a Few Lines
6.1. The Method of Line Breadth
That more than one parameter can be studied from one line in a Debye Scherrer pattern was noticed by Williamson & Hall who assumed that particle size and strain broadenings had Cauchy like distribution [14] . This means that the observed breadth of a line β is the sum of breadths due to particle size and strain i.e.
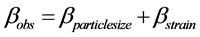
or

where t is the apparent particle size and e is apparent strain, θ is the angle of scattering and λ is the wave length scattered.
Thus
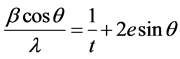 (25)
(25)
Plotting 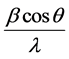 vs
vs , one can obtain the particle size t from the intercept one from the slope of the curve. Equation (25) is the well-known Williamson-Hall relation much used by many investigators [14] . Particle size and strain also can be determined by the famous Warren-Averbach method [15] .
, one can obtain the particle size t from the intercept one from the slope of the curve. Equation (25) is the well-known Williamson-Hall relation much used by many investigators [14] . Particle size and strain also can be determined by the famous Warren-Averbach method [15] .
6.2. The Method of Line Profile
Warren and Averbach showed that the Fourier Transform of a line profile yield significant information regarding particle size, particle strain, probability of faulting and many other crystal defects [15] . They also showed that an intensity profile can be expressed as a Fourier series
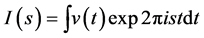 (26)
(26)
where v(t) is the Fourier Transform of the particle size, (st) stands for strain. For determining particle size and strain only, Warren and Averbach has developed a simple method [15] . Convert hkl reflection into h1k1l1, 2h12k12l1 etc. reflections by suitably changing axes as far as possible. Then let them be considered as 00l, 002l, 003l etc. by necessarily changing axes. Then write
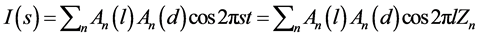
Now

For small value of l and n, the logarithm of the measured Fourier coefficient is given by

By plotting lnA(n) against l2 we obtain at l = 0, the value of 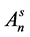 and from the slope,
and from the slope,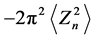 . The distance l = na3 is the undistorted distance a3Zn.
. The distance l = na3 is the undistorted distance a3Zn.
In general, Equation (26) can be written in a summation form
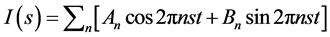
where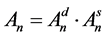 ,
, 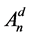 is the coefficient for particle size broadening,
is the coefficient for particle size broadening, 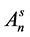 for strain. Warren and Warekois [16] showed that this causes a shift in peak position in 70.50 α brass and
for strain. Warren and Warekois [16] showed that this causes a shift in peak position in 70.50 α brass and  radiation.
radiation.
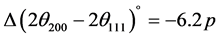
where p is the stalking fault probability. Also
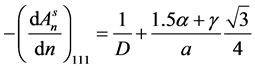
And

where γ is the twin fault probability, and a is the lattice constant.
7. Conclusion
The application of the above formulae depends on the recognition of the proper mathematical model. To achieve this, the best way is the  test devised by Mitra [5] to distinguish between Gauss and Cauchy profiles (described in [13] ). Plot of intensity vs the angle of curve will yield considerable information. For each peak—nonoverlapped by neighboring peaks, the corresponding intensity vs angle of scattering curve should be examined to determine if it belongs to Gaussian, Cauchy, Voigt and Pseudovoigt type and if so, the mixing parameter can be obtained by comparing with
test devised by Mitra [5] to distinguish between Gauss and Cauchy profiles (described in [13] ). Plot of intensity vs the angle of curve will yield considerable information. For each peak—nonoverlapped by neighboring peaks, the corresponding intensity vs angle of scattering curve should be examined to determine if it belongs to Gaussian, Cauchy, Voigt and Pseudovoigt type and if so, the mixing parameter can be obtained by comparing with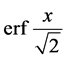 ,
, 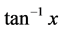 ,
,  ,
, 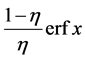 ,
,  and
and
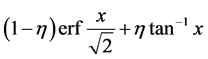 respectively. There is a likelihood of confusion between Gaussian, Voigt and Pseudovoigt of convolution type. This can probably be resolved by examining additional peaks. Similarly, determining particle sizes by trying the relevant formulae may be helpful. The advantage of this procedure is that overlapping of lines will not interfere with the determination of the parameters. It is important to note that the Fourth Cumulant is an important parameter—since it is the only parameter which can decompose the observed line profile into profiles for different reasons of line shape. By a reverse analysis of the shape of the diffraction profile, it should be possible to identify the nature of the line profile—Gauss, Cauchy, Voigt, Pseudovoigt and hence, of the mixing parameter. From these—it should be possible to determine the parameters of line broadening. It is expected to be a good test for pattern decomposition. In this connection, another test—the χ test due to Pearson and Hartley may be mentioned [13] .
respectively. There is a likelihood of confusion between Gaussian, Voigt and Pseudovoigt of convolution type. This can probably be resolved by examining additional peaks. Similarly, determining particle sizes by trying the relevant formulae may be helpful. The advantage of this procedure is that overlapping of lines will not interfere with the determination of the parameters. It is important to note that the Fourth Cumulant is an important parameter—since it is the only parameter which can decompose the observed line profile into profiles for different reasons of line shape. By a reverse analysis of the shape of the diffraction profile, it should be possible to identify the nature of the line profile—Gauss, Cauchy, Voigt, Pseudovoigt and hence, of the mixing parameter. From these—it should be possible to determine the parameters of line broadening. It is expected to be a good test for pattern decomposition. In this connection, another test—the χ test due to Pearson and Hartley may be mentioned [13] . , and this can be calculated for the Gauss, Cauchy, Voigt and Pseudovoigt functions using Formulae (15), (17) and (18). Pearson and Hartley have given numerical values to identify Pearson type IV and Pearson type VII curves as well [13] .
, and this can be calculated for the Gauss, Cauchy, Voigt and Pseudovoigt functions using Formulae (15), (17) and (18). Pearson and Hartley have given numerical values to identify Pearson type IV and Pearson type VII curves as well [13] .
Acknowledgements
Sincere and heartfelt thanks are due to Dr. Paramita M Ghosh of the University of California at Davis, California, USA for encouragement and helping in many ways and to Mr. Bishwajit Halder for secretarial help. The author was previously Professor and Head of the Department of Physics, Indian Institute of Technology, Kharagpur, West Bengal, INDIA.
NOTES
*Current Address: 284B Rash Behari Avenue, Kolkata—700019, West Bengal, India.