Taylor’s Power Law for Ecological Communities—An Explanation on Nonextensive/Nonlinear Statistical Grounds ()
1. Introduction
Nearly 35 years ago, Taylor and collaborators proposed the so-called Taylor’s model, based on the analysis of 156 sets of data from a wide range of species and sampling scales (from ciliates on the surface of a flat-worm to the human population of the United States of America). The model assumed that spatial variance (V) is proportional to a fractional power of the mean population density (M), that is [1]
 (1)
(1)
which can be represented by log-log plots as
 (2)
(2)
where α is a proportionality parameter and β was regarded as an index of aggregation, which takes a characteristic value for each species, reflecting the balance between opposing behavioral tendencies to move towards or away from centers of population density [1] -[3] .
Since then, the relationship between V and M has been established for more than 400 species in the taxa ranging from protists to vertebrates (see Figure 1). Although phenomenological interpretations have appeared elsewhere [4] , explanations for (a) the generality of Taylor’s finding, and (b) for the fact that 1 < β < 2, based on “first principles”, are still lacking. More recently, a comprehensive and lucid account by Cohen [5] explains why very different models lead to Taylor’s law. Additionally, he derived both the growth-rate theorem and the Taylor’s law from a simple model of exponential population dynamics, also displaying a link between them.
Elucidating the conceptual framework underlying Taylor’s power law, deeply rooted in fundamental principles (as addressed in Section 2.1 below), is quite relevant. In fact, addressing many current ecological problems such as population viability in conservation biology studies, pest dynamics in agriculture, species diversity and stability, and strategies for environmental monitoring, in general, requires a deep understanding of the relationship between a population’s variability (V) and its mean abundance (M). Moreover, understanding the facts that control diversity is high on the agenda for ecologists and conservationists, and different factors evidently operate on different scales.
In this sense, here, an interpretation for Taylor’s Power Law based on concepts for nonlinearity and nonextensivity is proposed, where the role played by the peculiarities of interactions (short-versus long-range) among the individuals of an ecological community is emphasized.
2. Present Approach
2.1. Complex, Nonextensive Systems
It has been realized that several complex systems exhibit an underlying structure ruled by shared organizing principles [6] . As a result, all parts of the system communicate with each other by means of long-range interactions (interconnectivity). The primary signatures of such a peculiarity are power-laws linking variables of the system in a nonlinear way. In this case, extensive statistics is no longer applicable, since the system variables are nonextensive in the sense that the sum of the system parts does not reproduce the whole system.
The issue we are proposing and addressing here is that power-laws naturally emerge when a long-range interaction is switched on, with no exception, even for interacting species in an ecological community. This is al-

Figure 1. Log-log plot of species variance (V) as a function of the mean abundance (M): Data points: Ourapteryx sambucaia (a), Olostygia multisgaria (b) and Phorodon humuli (c), three insect species. Straight lines: lines fits to the data points-adapted from [4] .
ready true in systems as small as the DNA molecule [7] , to those as large as galaxy conglomerates [8] . Taylor’s Power Law, with its fractionary exponent β (see Equation (1)), is inserted in this nonextensive/nonlinear scenario.
If we consider N a random variable (or, an extensive variable) representing population density, with finite mean M and variance V, the scaling N ® KN by a constant K that is, by promoting the same change (K) in all the values assumed by N, leads to:
 (3)
(3)
Since , V scales as
, V scales as
 ; (4)
; (4)
therefore,
 . (5)
. (5)
Now, if a power-law connects V with M, as in Equation (1), we have that  and
and ; taking the ratio we obtain;
; taking the ratio we obtain;
 . (6)
. (6)
Therefore, N is not an extensive variable. It remains to be shown what the nature of the interactions in ecological communities is.
2.2. Interactions in Ecological Communities
When modeling population dynamics, the identification of the following interaction categories is necessary [9] : (1) those taking place among the system components and its internal dynamics, and (2) between the system as a whole and the external world. In this last case, interaction is carried out through the interface (boundary conditions).
In the first category the following processes may be present: (a) reproduction and death rates driven by genetic peculiarities; (b) regulatory processes: responsible for the coordination of population activities within living space and time; (c) competitive processes, particularly when the quantity of available food is limited; and (d) communication processes.
While processes (a) and (b) take place in a small volume, comparative to the total size of the system, (c) and (d), in general, involve larger distances. As shown in the next section, it is precisely these long-range interactions that introduce nonlinearities in the system dynamics (as Taylor’s power law).
Unlike systems constituted by unanimated objects, living systems (animal and human species, in particular) have the ability to regulate the range of the interactions among their elements in response to environmental stimuli. Like some large predatory animals, ancestral humans also acted as groups (long-range interactions) when hunting large prey such as mammoths, but went out solitary (short-range interactions) for small prey such as antelopes [10] .
2.3. Our Approach: Random Walk + Long Range Correlations
In a system constituted of elements interacting by means of short-range forces, each of these elements interacts only with the elements of the system in close proximity to it. This interaction process can be described as a simple random walk. Because of the short-range character of the interaction, each element (which can be treated as a particle) undergoes random jumps to one of its nearest-neighbor sites, where the jump lengths are small. Let’s represent by  a vector pointing to a nearest-neighbor site; it represents the ith jump of the walk and
a vector pointing to a nearest-neighbor site; it represents the ith jump of the walk and 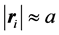 is the jump length.
is the jump length.
After n jumps, through a length , the net displacement is
, the net displacement is
 (7)
(7)
The probability for a particle to undergo a displacement  is a Gaussian distribution with the average displacement
is a Gaussian distribution with the average displacement  being [11]
being [11]
 (8)
(8)
Let’s now consider the squared displacement
 . (9)
. (9)
Since  and
and , the mean square displacement in n steps is
, the mean square displacement in n steps is  (since
(since ); thus,
); thus,
 (10)
(10)
The result displayed by Equation (10) follows from the assumption that the single jumps  are uncorrelated, i.e.,
are uncorrelated, i.e.,  , which is fine for short-range interactions, and its linearity expresses the extensive character of the system (the whole is the sum of the parts). However, Equation (10) needs to be modified for long-range interactions. It is plausible that the jumping correlations
, which is fine for short-range interactions, and its linearity expresses the extensive character of the system (the whole is the sum of the parts). However, Equation (10) needs to be modified for long-range interactions. It is plausible that the jumping correlations  are proportional to some sort of interaction potential between positions
are proportional to some sort of interaction potential between positions  and
and , defined as
, defined as , which may be written in quite general form as
, which may be written in quite general form as

thus,
 (11)
(11)
 and k are constants. Then, retaking Equation (9), we have for the mean square displacement after n steps
and k are constants. Then, retaking Equation (9), we have for the mean square displacement after n steps
 . (12)
. (12)
From this point on, a random walk is assumed taking place in the plane and that 2πrdr, a differential circular strip, is the elemental area for integration. Therefore,
 , (13)
, (13)
where we assume that the in-plane density of pairs , ρ, is constant. Moreover, since it is always possible to promote a coordinate translation such that
, ρ, is constant. Moreover, since it is always possible to promote a coordinate translation such that , and putting
, and putting , we get from Equations (11) and (13)
, we get from Equations (11) and (13)
 , (14)
, (14)
and substituting in Equation (12),
 . (15)
. (15)
For large  (or large
(or large ) and
) and  the first term,
the first term,  , becomes small relative to the second term; then (
, becomes small relative to the second term; then (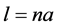 and
and )
)
 (16)
(16)
where for 1 < α < 2 the system is nonextensive. In the absence of an interaction potential the system is Brownian-like, that is, extensive.
Let’s assume that several independent series of measurements are carried out, and that for each series a mean , and its corresponding standard deviation
, and its corresponding standard deviation , is calculated. The probability distribution function for the
, is calculated. The probability distribution function for the ’s, given a certain number of degrees of freedom f, is [12]
’s, given a certain number of degrees of freedom f, is [12]
 (17)
(17)
For large  values and for
values and for  we obtain
we obtain
 . (18)
. (18)
If the dispersion σ around  is less than 20% (see Figure 2), we can assume
is less than 20% (see Figure 2), we can assume  (see Equation (16)), and substituting in Equation (18) we obtain
(see Equation (16)), and substituting in Equation (18) we obtain
 (19)
(19)
Therefore, it is here demonstrated that a power law emerges from a random walk when an interaction potential between consecutive jumps is introduced. In the present study, the random walk is the random variability of the mean population abundances M (see below).
3. Discussion
3.1. A Nonlinear Ecological Community
On the basis of our nonextensive statistical approach, it is now easy to understand that the ubiquity of Taylor’s power-law slopes in the interval 1 < β < 2 (Equation (1)), is intimately associated with long-range interactions among all the elements of the system. This conclusion is qualitatively correct.

Figure 2. Comparison between p values provided by Equation (17) (dash-curve) and the approximation introduced in Equation (18) (solid-curve). In the insert the relative difference between the approximate and the exact values is shown. It is salient that for a dispersion of the mean up to approximately 20% (low dispersion), the two distributions are nearly equivalent.
However, unraveling the peculiarities of such long-range interactions requires modeling, as recently carried out by Kilpatrick and Ives [4] . By using stochastic simulation and analytical models, they demonstrated how negative interactions among species in a community can produce slopes β < 2. There is a key parameter in their model,  , the competition coefficient giving the per capita effect of species j on species i. The simulations showed that when there are no species competitive interactions (that is, when
, the competition coefficient giving the per capita effect of species j on species i. The simulations showed that when there are no species competitive interactions (that is, when ) the exponent b (Equation (1)) averages 2. Therefore, the population dynamics of single species may be understood in terms of the dynamics of a nonextensive or an extensive system, provided these species are interacting or not within their ecological community. Nonlinear selection in natural populations, for instance, has been addressed by Blows and Brooks [13] by means of a complete application of a response surface methodology. Such nonlinearities arise because of the existence of correlation selection on pairs of traits which, in our random walk approach, is the equivalent of having
) the exponent b (Equation (1)) averages 2. Therefore, the population dynamics of single species may be understood in terms of the dynamics of a nonextensive or an extensive system, provided these species are interacting or not within their ecological community. Nonlinear selection in natural populations, for instance, has been addressed by Blows and Brooks [13] by means of a complete application of a response surface methodology. Such nonlinearities arise because of the existence of correlation selection on pairs of traits which, in our random walk approach, is the equivalent of having  (see Equations (11) and (14)).
(see Equations (11) and (14)).
3.2. Probability Distribution of M
The per capita variability in population abundances (P) is
 (20)
(20)
We note that the inverse function
 (21)
(21)
is proportional to the probability distribution of M, p(M), because the “normalized” behavior (increase or decrease) of M per unit of variability (that is M/V) is proportional to the probability function of getting a species abundance equal to M. In our working example the function P−1 = P−1(M) indicates that increasingly higher mean population abundances are increasingly less probable. Therefore, p(M) = M−δ (compare with Equation (19)).
The curves in Figure 3 were obtained from Equation (21) for β = 2 and 1.5, standing for extensive and nonextensive, respectively. It is quite salient that for β = 2 the probability for “rare events” is substantially smaller than

Figure 3. Linear-linear plot of the inverse function P−1 as function of M. The numbers in parentheses in the horizontal scale are logM. The solid and dashed curves represent the function given in Equation (21) for β = 2 and 1.5, respectively. In the insert the plot of the per capita variability P as function of M is shown.
in the case for β = 1.5. While random outcomes of probabilistic demographic processes generate differences in species characteristics, the longor short-range character of inter and intra-species interactions determines how their variability responds to increases in abundance.
While the big picture for large M is provided, the nonextensive approach does not alter the small M interval (rare species regime) because the extensive and non-extensive curves converge for M à 0. This is, by any means, a nontrivial regime since rare species grow differentially faster than common species and, therefore, move up and out of the rarest abundance categories owing to their rare-species advantage [14] . In fact, estimating the proportion of rare species in particular habitats is a major concern for ecologists. There is, however, no way to achieve effective conservation of both resilience and interconnectivity without the massive input of science.
In nonextensive scale-free ecological communities (see the Appendix), species are therefore more stable in the sense that, for a given and fixed variance unity, the probability of forming larger populations (see Figure 2) is greater compared to statistically extensive communities. As shown elsewhere [15] , computer networks with scale-free architectures, such as the World Wide Web, are not at all prone to accidental failures. Quite revealing in this regard, computer simulations and calculations performed by Albert and Barabási [16] have shown that a growing network with preferential attachment becomes scale-free. This is precisely what was observed in our scale-free networked biological system: growth (increasing M) and preferential attachment (the negative interactions among species). These two ingredients are at the genesis of many other biological system organizations.
In this context, Taylor’s power-law thus showcases a convincing example of nonextensivity in a biological organization, and in our approach the long-range interaction as its key ingredient is identified.
4. Final Remarks
Once it is agreed that an ecological community behaves as a network of interconnected elements, the most profound statistical aspects regulating its functioning can be accessed and, as a consequence, new insights for the conception of new models are gotten, while existing ones are improved. Until now, for instance, there has been no analytical derivation of the expected equilibrium distribution of relative species abundance in the local community, and fits to the theory have required simulations [17] .
Additionally, as a nonlinear, scale-free network, an ecological community would be entitled to exhibit selforganization (see Appendix), a property lying at the root of life organization itself. In fact, self-organization is the spontaneous emergence of new structures and of new behavior patterns (in animal populations), characterized by internal feedback links and mathematically described by means of nonlinear equations.
It would appear to us to be a laudable attempt to divulge basic concepts of nonextensivity, and some of their most important applications in life sciences, more widely.
Acknowledgements
This work was supported by grants from FAPESP, CAPES and CNPq, Brazilian funding agencies for the promotion of science.
Appendix: Scale-Invariance and Self-Organization
We can show that the power-law in Equation (1) is, in contemporary parlance, equivalent to the scale-invariant relationship
 (22)
(22)
Since l is arbitrary, we can put λ = 1/M in Equation (22); thus,
 (23)
(23)
that is, Equation (1) is obtained.
Any function V = V(M) satisfying Equation (22) is a homogeneous, scale-invariant function in the sense that if the scale of measuring M, namely, from M to  is changed, the new function
is changed, the new function  has the same form as V(M).
has the same form as V(M).
A scale-invariant system must be self-similar and vice versa. As a consequence, self-organized criticality (SOC) may be attained (for a lucid and pedagogical account the reader is referred to [8] ). The dynamics of the system exhibiting SOC may undergo active walk, where elements of the system communicate with their environment, and not only with the landscape have they shared. The principle of active walk has been applied with success to biology related problems such as the cooperation of ants in food collection [18] for example.