1. Introduction
We give a piercing epistemological reappraisal of Einstein’s E = mc2 in the light of Magueijo-Smolin theory of the varying speed of light. One of the most important conclusions of the work is that what appears in the first instance to be a limitation of E = mc2 where m is the mass and c is the speed of light, is in fact far more a generality than even Einstein could have considered possible. Similarly Magueijo-Smolin’s extension of E = mc2 namely
 (1)
(1)
where Ep is the Planck energy was found to actually unify classical kinetic energy with Einstein’s formula as well as the three formulas of quantum relativity recently developed by the author:
 (2)
(2)
 (3)
(3)
and
 (4)
(4)
where E(O) is the measured 4.5% energy of the cosmos while E(D) is the 95.5% dark energy supposed to be behind the observed surprising accelerated expansion of the universe. Finally we show that ’tHooft-Veltman D = 4 ‒ ε dimensional regularization can be used to find E1 and E2 by not letting ε → 0 but instead setting ε = 2ϕ5 where ϕ5 is Hardy’s quantum entanglement and D ‒ k is the fractal Hausdorff dimension at the energy scale of grand unification, i.e. 1016 GeV.
2. Motivation of the Present Analysis
The title of the present paper is obviously a pun on a recent excellent book by a gifted scientist and science communicator [1] . The present work will be in keeping with the title and shows beyond any reasonable doubt that E = mc2 consists really of two parts. First the ordinary energy which we can measure directly and this is given by E1 of a quantum particle (O) and is equal to the mass m multiplied with the speed of light c squared and divided by 22 [2]
 . (5)
. (5)
The second part is the energy E2 which is the energy which we cannot measure in any direct way and call therefore dark energy [3] . This energy we attribute essentially to the quantum wave (w) guiding the particle, i.e. the quantum particle (O) as it propagates. This E2 is given also by a similar formula [4] [5]
 (6)
(6)
Remarkably both E1 and E2 add to exactly Einstein’s famous equation
 (7)
(7)
3. Particle-Wave Duality from Einstein’s Relativity
Readers familiar with the particle-wave duality of quantum mechanics [6] -[10] will by now have surmised that the split of E in E(O) and E(D) must be related to a quantum dissection of some sort but must be mystified by why the involved factors are 1/22 and 21/22 apart of what the meaning and relevance of this new presentation is. Before explaining this crucial point I rather regress and recount the inner dialogue of the author when he wrote down E1 = mc2/22 for the first time around the beginning of May 2011. He was initially motivated by the missing 95.5 percent energy density of our cosmos which we have since dubbed dark energy and he immediately thought Einstein made a mistake for which he could not be blamed because he knew nothing at the time which could possibly make him doubt his derivation or suspect that something called quantum mechanics has a great deal to say about the nature of space-time and the number of messenger particles. The first public presentation of E = mc2/22 was in a small international conference in Alexandria, Egypt in 2012 and the second was a detailed account presented in a mini symposium in Shanghai [11] -[13] . Ironically the author had to stand vis-à-vis himself corrected because Einstein’s E = mc2 was not missing something he did not know about and could not be blamed for but because his famous equation included quantum gravity effects for which Einstein could not be commended since quantum mechanics was not there at all nor even around the corner [14] -[17] .
4. Grappling with Dark Energy
With the benefit of hindsight everything is clear. Looking back at the genesis from mc2 to mc2/22 and mc2 (21/22) and to close the circle again with (mc2/22) + mc2 (21/22) = mc2 we gain a deep insight by looking back as far as Newton’s (1/2)mv2. All of this could not have possibly happened without the incredible cosmological measurements and observations such as COBE, WMAP and Planck [18] -[22] by courageous scientists who were determined not to ignore measurements, observations and real experiments regardless [18] of how famous and accepted a theory is if it does not account for a rational explanation of the phenomenon in question [22] . To be sure E = mc2 is so famous that it takes more than scientific courage to even attempt to question it [23] -[27] . In Figure 1 and Figure 2 we present the uninitiated reader with a visual proof of the degree of adoration which this

Figure 1. From here to eternity and from Egypt to China, Einstein’s masterpiece of art eternalizes human high culture. In this real photograph only the quantum particle Lorentzian factor 1/22 was inserted into the photo taken in 2013 by the renowned Chinese applied mathematician, engineer and physicist Ji-Huan He. The complete dissected equation is of course (mc2/22) + mc2 (21/22) = mc2. The photo and E = mc2 should be viewed with the sensitive eye of say the recent film of George Clooney and Matt Damon “The Monuments Men” , Columbia and Twentieth Century Fox (2014).

Figure 2. A monument in modern united Germany for E = mc2 against a background of a building in the land of “Dichter und Denker”. However poetry, philosophy and art must be protected by international institutions which really believe in and defend the freedom of human thoughts enshrined in the work of Leonardo, Michelangelo, Beethoven, Mozart and Albert Einstein’s E = mc2 with or without the Lorentzian factors g(O) = 1/22 and g(D) = 21/22 discussed at length in the present work.
admittedly super elegant equation enjoys [1] [2] . It was of course a delightful surprise to see the statue of Einstein as well as his E = mc2 when the author gave his lecture on E = mc2 and found the sculpture in the university garden of Soochow University (see Figure 1), China in 2013. The world wide web hosts hundreds of thousands of pictures, photos (see Figure 2) and popular totally unscientific accounts of E = mc2 that it became indeed a heroic task for any scientific critique to be noticed let alone be listened to and seriously considered [26] [27] . Never the less our present task is relatively easy because E = mc2 is not only right but far more right than its creator imagined provided we explain why it is so which we deal with in the following sections. On the other hand grappling with E = mc2 to show that E = mc2/22 is the ordinary energy of the quantum particle while E @ mc2 (21/22) is the dark energy of the quantum wave was not that simple [2] -[16] .
5. The Lagrangian Which Einstein Never Wrote Down
Nowadays no one would dare to tackle a fundamental problem in high energy physics without writing first a Lagrangian [9] [10] . To be sure the Lagrangian method is just one of two basic ways of establishing the governing equation of motion, steady state or equilibrium equations. Einstein did not take the Lagrangian way. Let us supposed he did and see what comes out of this journey to the past. First Einstein’s Lagrangian would most probably have a single degree of freedom, namely the photon. Let us pause here a moment. We have known since quite some time that nature is described by 12 photon-like particles all predicted theoretically and found experimentally since a long time [5] [6] [10] [14] but of course long after Einstein wrote his equation. Could we predict the effect of this drastic reduction in the real number of degrees of freedom of “Einstein’s” Lagrangian from the 12 of the standard model [5] [9] , i.e. |SU(3) SU(2) U(1)| = 8 + 3 + 1 = 12 to the single photon γ degree of freedom |U(1)| = 1 where SU(n) and U(1) are Lie symmetry groups representing elementary messenger gauge bosons following Noether’s famous theorem. Well the result is also well known from a very famous theorem on Eigenvalue due to Lord Rayleigh [28] . This theorem asserts that by reducing ‘artificially’ the number of degrees of freedom leads to an over estimation of the Eigenvalue. Examples for Eigenvalues in structural and mechanical engineering [28] are the Eigen frequencies and buckling loads. For instance solving a problem using a Rayleigh or Ritz trial function [28] will always lead to a frequency or a buckling load which is always larger and never smaller than the exact one [28] . Now comes the important step when we recall that energy levels are the Eigenvalue of Einstein’s fictitious Lagrangian exactly as they were the Eigenvalue of the Schrödinger equation [9] . Consequently E = mc2 is first an Eigenvalue and second, it is a much larger Eigenvalue than we should have, that is if the photon would have been only a particle. However a photon is a particle as well as a wave because it is a quantum particle. It would be a shrewd guess indeed if we surmise that E = mc2 should be reduced in reverse proportionality to the reduction from 12 to 1, i.e. a factor of 1/(12 ‒ 1). This may be too simplistic a way of looking at things but reality is not very far off as we will see momentarily. The point is that 1/(12 ‒ 1) = 1/11 is equal the Lorentz factor γ(0) is correct provided we undo part of what special relativity did to Newton’s kinetic energy EN = (1/2)mv2 and includes 1/11 not in E = mc2 but in EN provided we let the velocity v → c so that we find
 (8)
(8)
This is the result we previously obtained using various sophisticated methods. We note that the decisive factor of 22 could be interpreted as the number of p-forms living in a K3 Kähler space of a compactified type IIA string theory where b2 = 22 plays the role of massless boson-like photons.
6. Intermediate Discussion
Before going any further let us give a naïve and from a special relativity view point flawed explanation for why the half in Newton’s kinetic energy becomes unity when the velocity v becomes the speed of light c. The point could be superficially explained by the constancy of the speed of light which allows us to take it out of the integration sign:
 (9)
(9)
where m is classically a constant, x is the distance,  and t is the time. Having naïvely assumed that
and t is the time. Having naïvely assumed that  was never any value except c, i.e. the speed of light, then we can find Einstein’s energy in a truly “cheap” way by writing
was never any value except c, i.e. the speed of light, then we can find Einstein’s energy in a truly “cheap” way by writing
 (10)
(10)
However, there are several fallacies here or so it appears. First  does not change with t because
does not change with t because  is a constant equal c. Second and more importantly at c the mass becomes infinitely heavy and therefore only massless particles which can move with the speed of light are admitted. On the other hand this is the same problem with E = mc2 no matter how Einstein derived it he did indeed derive this formula in many sloppy and wrong ways to the extent that one wonders how Einstein came to this formula in the first place. The point however is that Einstein meant this formula to be not in “actuality” but in Aristotle’s “potentia” previously discussed by Heisenberg in connection with quantum mechanics [29] and much later by the author [30] [31] . That would be a good way out for explaining dark energy. We could argue then that the part of the energy which we can measure, i.e. the 4.5% given by E(O) = mc2/22 is the part where the velocity grows from v = 0 to v = c and that it grows in a way which could be described as nonlinear bringing with it a factor much smaller than the 1/2 of Newton’s kinetic energy. At the edge of the universe in the proximity of the infinity holographic circle, the energy we have is associated with the average speed which coarse grains this velocity from zero to infinity and comes up with a constant expectation value equal to what we call the constant speed of light. That is where the factor (21/22) comes from. Thus starting from a mathematically quite “dodgy” derivation of E = mc2 we see that we can give a reasonable and rather rational explanation for the outrageous reality and the facts of a human scale observer living squeezed between the micro quantum world and the large structure of the relativistic universe. Seen from the human perspective, the entire existence is infinite in all directions [32] . Could we then extend the preceding insight to explain the position of Newton’s kinetic energy which we use to derive E(O) = mc2/22 and E(D) = mc2(21/22) from a five dimensional zero set D(O) = (0, ϕ) and a five dimensional empty set D(
is a constant equal c. Second and more importantly at c the mass becomes infinitely heavy and therefore only massless particles which can move with the speed of light are admitted. On the other hand this is the same problem with E = mc2 no matter how Einstein derived it he did indeed derive this formula in many sloppy and wrong ways to the extent that one wonders how Einstein came to this formula in the first place. The point however is that Einstein meant this formula to be not in “actuality” but in Aristotle’s “potentia” previously discussed by Heisenberg in connection with quantum mechanics [29] and much later by the author [30] [31] . That would be a good way out for explaining dark energy. We could argue then that the part of the energy which we can measure, i.e. the 4.5% given by E(O) = mc2/22 is the part where the velocity grows from v = 0 to v = c and that it grows in a way which could be described as nonlinear bringing with it a factor much smaller than the 1/2 of Newton’s kinetic energy. At the edge of the universe in the proximity of the infinity holographic circle, the energy we have is associated with the average speed which coarse grains this velocity from zero to infinity and comes up with a constant expectation value equal to what we call the constant speed of light. That is where the factor (21/22) comes from. Thus starting from a mathematically quite “dodgy” derivation of E = mc2 we see that we can give a reasonable and rather rational explanation for the outrageous reality and the facts of a human scale observer living squeezed between the micro quantum world and the large structure of the relativistic universe. Seen from the human perspective, the entire existence is infinite in all directions [32] . Could we then extend the preceding insight to explain the position of Newton’s kinetic energy which we use to derive E(O) = mc2/22 and E(D) = mc2(21/22) from a five dimensional zero set D(O) = (0, ϕ) and a five dimensional empty set D( 1) = (
1) = ( 1, ϕ2) respectively where
1, ϕ2) respectively where  [4] ? A tentative affirmative answer to this question could be as follows: In classical mechanics we have two types of energy. Thus for the position potential energy and the kinetic energy of motion of a falling stone of mass m from a height h under the force of gravity the sum of both energies at the starting and end points must remain the same. Consequently when the stone is stationary at height h it has a real position energy mgh and an Aristotlean kinetic energy “in potentia” [29] -[31] equal (1/2)mv2. The reverse then is also true when after falling the distance h and just before hitting the fully elastic “floor”, the kinetic energy is actually fully operational while the position energy is factually zero and exists only “in potentia” for instance by reversing direction and bouncing back due to the perfect elastic floor assuming of course that there is no air resistance nor any friction losses. What we are laboring at is to twist things a little constructively as to say that position energy and kinetic energy are equal and that therefore the total energy is the sum of both energies leading to replacing the factor 1/2 by a factor 1 which as reasoned earlier could only be done when we replace v by its expectation average, namely
= c
[33] .
[4] ? A tentative affirmative answer to this question could be as follows: In classical mechanics we have two types of energy. Thus for the position potential energy and the kinetic energy of motion of a falling stone of mass m from a height h under the force of gravity the sum of both energies at the starting and end points must remain the same. Consequently when the stone is stationary at height h it has a real position energy mgh and an Aristotlean kinetic energy “in potentia” [29] -[31] equal (1/2)mv2. The reverse then is also true when after falling the distance h and just before hitting the fully elastic “floor”, the kinetic energy is actually fully operational while the position energy is factually zero and exists only “in potentia” for instance by reversing direction and bouncing back due to the perfect elastic floor assuming of course that there is no air resistance nor any friction losses. What we are laboring at is to twist things a little constructively as to say that position energy and kinetic energy are equal and that therefore the total energy is the sum of both energies leading to replacing the factor 1/2 by a factor 1 which as reasoned earlier could only be done when we replace v by its expectation average, namely
= c
[33] .
7. The Larger Picture Afforded by E = mc2
Thus nor surprisingly in view of what we just mentioned, the total energy is nothing but Einstein’s maximal energy E = mc2. Seen that way the ordinary energy part of the 5D quantum particle E(O) = mc2/22 could be likened to the position energy or the energy of rest which we can measure without worrying about the state vector reduction of quantum mechanics while the 5D quantum wave energy which we identified with the dark energy component of E = mc2 could be likened to the kinetic energy of propagation and is given by E(D) = mc2(21/22). Sure enough the sum turns out to be that of Einstein’s total energy which we ceaselessly mention all the time because of its enormous importance. It is the living proof that Einstein could not be blamed for not noticing that E(O) = mc2/22 nor could he be praised for realizing that E(D) = mc2(21/22) despite tinkering at least initially with the idea of the cosmological constant which many researchers see as the explanation for dark energy and the accelerating expansion of the universe for which there are of course other even more imaginative scenarios [34] -[36] , in particular that based upon Banach-Tarski paradoxical decomposition [37] . However, what Einstein must be credited with in no minor measure is an audacity to stick to a certain intuitive picture of a philosophical “Anshaung” despite fierce opposition and the tremendous mathematical difficulties.
8. The Pioneering Work of Magueijo and Smolin
It is of course politically unwise and definitely risky to criticize Einstein. Some do indeed criticize Einstein just to be credited with having criticized Einstein maybe to achieve an Andy Warhol deceptive five minutes of fame. However there are genuine people among those who dared to question E = mc2. For me Mageuijo is the most prominent of them all not only for having the undeniable courage to criticize the scientific establishment, the Editor of Nature [34] as well as science policy apart of Einstein’s relativity but still remaining not only respectful of Einstein and his E = mc2 but also for being right and to the mind of the author, deadly right [35] -[37] . Working together with seasoned and philosophically subtle Lee Smolin, Magueijo established the correct form of E = mc2 when generalized to a “quantum gravity” formula. His elegant result reads
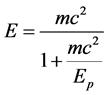 (11)
(11)
where Ep is the Planck energy [34] [35] [37] . This is completely equivalent to fusing EN = (1/2)mv2, E = mc2 and my two equations E(O) = mc2/22 and E(D) = mc2 (21/22) into a single equation. Of course Magueijo was there before the present author. However, he did not quantify his result and consequently he did not notice the relation to dark energy nor the connection to the bosonic string theory and high energy particle physics and Witten’s M-theory [2] -[4] [36] [37] . On this count the author thinks he was there first although overall it is without any doubt the achievement of Magueijo-Smolin’s work and the school of doubly special theory of relativity and varying speed of light which has the precedence on the author’s contribution [36] [37] . The ultimate irony however is that all the preceding results could be obtained directly and with unheard of elegance and simplicity from an old theory due to ’tHooft and Veltman and that we consider next.
9. Dark Energy from ’tHooft-Veltman Dimensional Regularization
Deriving dark energy from dimensional regularization [38] [39] was an unexpected application indeed for ’t Hooft-Veltman renormalization method. In a nutshell the mathematical-physical story starts by noticing first that using D = 4 ‒ ε instead of D = 4 in a perturbative solution and then letting ε → 0 overcome the disastrous infinities [38] . However, in Cantorian-fractal space-time ε has a definite mathematical, quantum mechanical as well as physical geometrical meaning. It turns out that ε = k and  where
where  is Hardy’s generic quantum entanglement and
is Hardy’s generic quantum entanglement and . Since Einstein used a smooth D = 4 space-time continuum to reach E = mc2, the
. Since Einstein used a smooth D = 4 space-time continuum to reach E = mc2, the  non-correlated mathematical space of ’tHooft-Veltman before letting ε = k → 0 have a geometrical topological meaning, namely being a fractal-Cantorian space-time [2] [3] [7] [29] [39] . This fractal space-time corresponds to an energy at which gravity correction to the running of gauge forces coupling constant becomes substantial [38] -[40] . This is easy to see by taking the 6th golden mean scaling of the electromagnetic
non-correlated mathematical space of ’tHooft-Veltman before letting ε = k → 0 have a geometrical topological meaning, namely being a fractal-Cantorian space-time [2] [3] [7] [29] [39] . This fractal space-time corresponds to an energy at which gravity correction to the running of gauge forces coupling constant becomes substantial [38] -[40] . This is easy to see by taking the 6th golden mean scaling of the electromagnetic  i.e. quasi differentiation of the electromagnetic field and noting that this is equal to 4 ‒ k because [39]
i.e. quasi differentiation of the electromagnetic field and noting that this is equal to 4 ‒ k because [39]
 (12)
(12)
which tends to 4 as k tends to zero [39] . However, unlike ’tHooft and Veltman we do not let k be neglected compared to the unity in the ratio (4 ‒ k)/4 and used instead as a scaling component of E to find E(Dark). Consequently we have
 (13)
(13)
Ordinary energy on the other hand is obviously given by
 (14)
(14)
exactly as expected. In conclusion we note that we expect that D = 4 ‒ k to physically exist between the GUT monopole energy, i.e. 1016 GeV and the Plankton energy of 1019 GeV. In other words and unlike how ’tHooft and Veltman view initially their method, we regard D = 4 ‒ k as a real fractal state of space-time and not a mere mathematical trick [38] [39] . The so found two expressions are in no respect less elegant and compact than Einstein’s beauty.
10. Conclusion
Einstein’s iconic formula E = mc2 is correct but far from being the whole story. By historical accident or providence Einstein struck on a quantum gravity formula disguising as a harmless maximal relativistic energy. E = mc2 is really made up of two parts, the ordinary measurable energy E(O) = mc2/22 and the dark energy plus dark matter component E(D) = mc2 (21/22). It seems that the only theory which can potentially draw the same conclusion and even more is first the Magueijo-Smolin theory of the varying speed of light and the compact and elegant corresponding formula E = mc2/[1 + (mc2/Ep)]. The second theory is our transfinite modification of ‘tHooft and Veltman [38] [39] . The present result has far reaching consequences for cosmology and how we view nature and the initial singularity as well as mans’ place in such a fractal-Cantorian universe [41] .