
1. Introduction
It is well known that seeking exact solutions for nonlinear evolution equations (NLEES) plays an important role in mathematical physics. In the past five decades or so, many effective methods have been presented, which contain the inverse scattering method [1] , Hirota bilinear method [2] , the tanh-function method and its various extension [3] [4] , the sine-cosine function method [5] [6] , homogeneous balance method [7] [8] , Jacobi elliptic function method [9] [10] , the first-integral method [11] [12] , the sine-Gordon equation method [13] and the Exp-function method [14] -[16] .
Recently, Wang et al. [17] proposed a new method called the  -expansion method to look for travelling wave solutions of nonlinear evolution equations (NLEEs). The
-expansion method to look for travelling wave solutions of nonlinear evolution equations (NLEEs). The 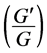 -expansion method is based on the assumptions that the travelling wave solutions can be expressed by a polynomial in
-expansion method is based on the assumptions that the travelling wave solutions can be expressed by a polynomial in  as follows:
as follows:
 (1)
(1)
where  satisfies a second order linear ordinary differential equation (LODE):
satisfies a second order linear ordinary differential equation (LODE):
 (2)
(2)
where ,
,  ,
, 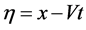 , and
, and  is a constant. The degree of the polynomial can be determined by considering the homogeneous balance between the highest order derivative and nonlinear terms appearing in the given NLEE. The coefficients of the polynomial can be obtained by solving a set of algebraic equations resulted from the process of using the method. By using the
is a constant. The degree of the polynomial can be determined by considering the homogeneous balance between the highest order derivative and nonlinear terms appearing in the given NLEE. The coefficients of the polynomial can be obtained by solving a set of algebraic equations resulted from the process of using the method. By using the  -expansion method, many nonlinear equations [17] -[27] have been successfully solved.
-expansion method, many nonlinear equations [17] -[27] have been successfully solved.
In the present paper, we will extend the  -expansion method to the following generalized Benjamin equation:
-expansion method to the following generalized Benjamin equation:
 (3)
(3)
where  and
and  are constants. Equation (3) is used in the analysis of long wave in shallow water; see [28] . To the best of our knowledge, there are a few articles about this equation. Recently, by applying the extended tanh method, Taghizadeh et al. [29] obtained some exact solutions. In the subsequent section, we will illustrate the
are constants. Equation (3) is used in the analysis of long wave in shallow water; see [28] . To the best of our knowledge, there are a few articles about this equation. Recently, by applying the extended tanh method, Taghizadeh et al. [29] obtained some exact solutions. In the subsequent section, we will illustrate the  -expansion method in detail with the generalized Benjamin equation.
-expansion method in detail with the generalized Benjamin equation.
2. Exact Solutions to the Generalized Benjamin Equation
First, in this section, we start out our study for Equation (3). Firstly, making the following wave variable
 (4)
(4)
where , and
, and  are constants to be determined later, Equation (3) becomes the ODE
are constants to be determined later, Equation (3) becomes the ODE
 (5)
(5)
where the prime denotes the derivation with respect to . Integrating Equation (5), twice and setting the constant of integrating to zero, we obtain
. Integrating Equation (5), twice and setting the constant of integrating to zero, we obtain
 (6)
(6)
Then, making the following transformation
 (7)
(7)
We can obtain an equation for  as
as
 (8)
(8)
Now, we make an ansatz (1) for the solution of Equation (8). Balancing the terms  and
and  in Equation (8) yields the leading order
in Equation (8) yields the leading order . Therefore, we can write the solution of Equation (8) in the form
. Therefore, we can write the solution of Equation (8) in the form
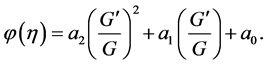 (9)
(9)
Substituting (2) and (9) into (8), collecting the coefficients of 
 and set it to zero we obtain the following system of algebraic equations for:
and set it to zero we obtain the following system of algebraic equations for: ,
,  ,
,  ,
,  ,
, 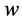 ,
,  and
and :
:

Solving the above system by Matlab gives
 (10)
(10)
 (11)
(11)
where ,
,  , and
, and  are arbitrary constants.
are arbitrary constants.
Substituting (10) (11) into (9) yields:
 (12)
(12)
where .
.
Substituting the general solutions of Equation (2) into the formulae (12) we have three types of travelling wave solutions of the generalized Benjamin equation as follows:
When ,
,
 (13)
(13)
where ,
,  ,
, 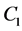 and
and 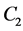 are arbitrary constants. It is easy to see that the hyperbolic solution (13) can be rewritten at
are arbitrary constants. It is easy to see that the hyperbolic solution (13) can be rewritten at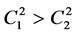 , as follows
, as follows
 (14)
(14)
while at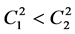 , one can obtain
, one can obtain
 (15)
(15)
where .
.
When ,
,
 (16)
(16)
where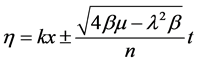 ,
,  ,
,  and
and  are arbitrary constants. Similarity, it is easy to see that the trigonometric solution (16) can be rewritten at
are arbitrary constants. Similarity, it is easy to see that the trigonometric solution (16) can be rewritten at 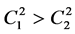 and
and , as follows
, as follows
 (17)
(17)
and
 (18)
(18)
where .
.
When ,
,
 (19)
(19)
where ,
, 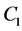 and
and  are arbitrary constants.
are arbitrary constants.
Authors [29] have looked for exact solutions of Equation (3) using the wave variable , Equation (3) should become the ODE
, Equation (3) should become the ODE
 (20)
(20)
not the ODE (7) in [29] in the following form
 (21)
(21)
Therefore, the exact solutions given in [29] are wrong. To the best of our knowledge, solutions (13), (16) and (19) have not been reported in literature.
3. Conclusion
The  -expansion method has been successfully applied here to seek exact solutions of the generalized Benjamin equation. As a result, a series of new exact solutions are obtained. The solution procedure is very simple and the travelling wave solutions are expressed by the hyperbolic functions, the trigonometric functions and the rational functions. To the best of our knowledge, these solutions have not been reported in literature. It is shown that the
-expansion method has been successfully applied here to seek exact solutions of the generalized Benjamin equation. As a result, a series of new exact solutions are obtained. The solution procedure is very simple and the travelling wave solutions are expressed by the hyperbolic functions, the trigonometric functions and the rational functions. To the best of our knowledge, these solutions have not been reported in literature. It is shown that the 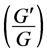 -expansion method provides a very effective and powerful mathematical tool for solving nonlinear equations in mathematical physics.
-expansion method provides a very effective and powerful mathematical tool for solving nonlinear equations in mathematical physics.
Acknowledgements
This work was supported by the research project of Yuncheng University (No.YQ-2011013, YQ-2011068, XK- 2012004).